不同海流流向下海底管道牵引过程中的动力学响应
赵望奇,朱克强*,张大朋,王自发
(1.宁波大学海运学院,宁波315211;2.海工国际工程有限责任公司,天津300456)
海洋工程
不同海流流向下海底管道牵引过程中的动力学响应
赵望奇1,朱克强*1,张大朋1,王自发2
(1.宁波大学海运学院,宁波315211;2.海工国际工程有限责任公司,天津300456)
参考海底管道牵引的相关文献,结合管道侧拉的具体过程,利用大型水动力分析软件OrcaFlex建立了管道牵引的动力学响应简化模型。通过改变海流方向和对牵引点A进行时域水动力分析,得到了不同海流流向对管道牵引过程的影响和管道牵引的最佳海流流向,确定了管道在经过牵引通道和出油管时易发生应力集中现象。结合水动力分析结果,给出了牵引过程中管道的力学性能和牵引的注意事项。
管道牵引;OrcaFlex;水动力分析;不同海流流向
由于世界经济的快速发展,石油、天然气这些最重要的能源不断地被消耗。陆地上的能源经过近百年的开采,能够开采的量逐渐地减少。于是,海洋成为了人们新的关注点。随着,海上石油工业的不断发展,海上的石油气运输也像陆上石油气一样繁忙。所以海洋管道在油气运输中起着越来越重要的作用。
海底管道作为输送海底石油气的关键,其敷设和安装一直是海洋工程界研究重点。一般来说,把管道敷设到海底预定位置大致有三大类:漂浮法、牵引法、铺管船法。当管道经由拖管船或其他设备抵达安装位置后,则需连接至导管架平台。而连接方法可分为:短管法、侧拉法、J型管牵引法、连接并埋设法和Stalk⁃on法等。国内外就S型和J型管牵引法的研究较多[1-4],而其他牵引法的研究则较少。其中,黄玉盈等[5]以弹性杆理论为基础,考虑了地基变形和摩擦力对管线的影响,提出了海底管线在铺设牵引时的二维静力模型,并率先采用幂级数法和奇异摄动法相结合的方法对力学模型进行求解。梁振庭[6]建立了一系列管道的三维有限元模型,对管道铺设牵引过程中的弯曲、应变等问题进行了研究。李旭[7]以漂浮牵引法与底拖牵引法的拖管过程为主要研究对象,分析了管线的受力状况和强度,但海流对管道牵引的影响并没有进行仔细地说明。唐立志[8]等采用有限元方法分析了在不同海流下管道的应力等因素,并提出了一些可行的方案,但这些方案并不足够具体和细致。实际工程中的侧拉法是管道由一条拖揽或固定锚引出多根拖揽拉向目标的一种牵引方法[9]。但是其相对于一般牵引法难以对齐导管架的接口。所以本文将使用一种类似门的牵引通道和两段牵引来限制管道的牵引方向,从而完成管道的对接工作。
本文运用国际大型水动力软件OrcaFlex建模,通过时域耦合动力学分析计算了在不同海流下,该牵引法下管道的水动力响应,并结合水动力性能计算结果给出一些指导性的意见。
1 OrcaFlex中的理论基础
OrcaFlex软件中的整体坐标,采用右手坐标系统。整体坐标的原点设在海平面上。Z轴方向垂直向上,X和Y方向满足右手定则。在画模型时,一般采用局部坐标,在确定整体位置时,采用整体坐标。此次建立的模型则是通过参考整体坐标来确定每个模型部件的分布位置,从而完成模型的建立。
在对牵引的管道进行轴向张力、剪力以及整个系统的耦合动态响应计算时,需将管道定义为挠性部件。在OrcaFlex中,牵引管道的性能相当于一个非线性弹簧,所以一般采用凝集质量法来建模。整根管道由若干个连续的、无质量和处于各个分段中点处的节点组成,并将其模拟为轴向、旋转弹簧和阻尼器的组合体。由于节点处于两个分段的中点,所以节点将集中这两个分段一半的质量,力与力矩都作用在节点处。
为了更好说明OrcaFlex中的理论基础,需一定程度上了解在该数值模型中的牵引管道。牵引管道的全长为550 m(有2 m的牵引端,牵引端的外径为0.3 m),外径为0.142 m。且在经过等效计算后,牵引管道的等效弯曲刚度为60 kN·m2,等效轴向刚度为269 000 kN,等效碰撞刚度为10 000 kN·m。
在管道牵引中,管道需满足一定的负浮力。单位长度的负浮WP为

式中:W为单位长度管道重量;b为单位长度管道浮力。根据工程实际经验,当管道采用牵引法是负浮力应为150~300 N/m。在该模型中,管道的负浮力为250 N/m,满足工程要求。而且本文选用的海流速度为0.5 m/s,所以即使考虑海流升力的影响,管道的负浮力也大于150 N/m。
当管道的负浮力确定时,则单位长度管道的摩擦力 f为

式中:FLC为由海流产生的升力;μ为管道与海底摩擦系数,一般为0.5~0.7,本文取0.5。
管道在牵引过程中暴露于稳定海流中,而流体拖曳力与稳定海流速度有关。拖曳力主要由管道前方的高压区和管道后方尾流中的低压区所造成的。管道单位长度的横曳力分量

式中:CD为横向拖曳系数;vn为水质点横向速度;ρ为海水密度;D为管道外径。
管道单位长度的纵向力,完全可以通过完整的Morison公式确定。纵向力为

式中:ρ为海水密度;D为管道外径;U为瞬时(基于时间)流速;y为管道纵向位移;CD为拖曳系数,CM为惯性系数。但由于海流速度为稳定的0.5 m/s,所以惯性力可以进行忽略。
对于牵引管道的有效张力可以用以下的公式计算

式中:Te表示有效张力;P0表示外部压力;Tw表示壁面张力;EA是缆轴向刚度;ε=(L-λL0)/λL0是总的轴向平均应变,λ是分段伸长系数,L0是分段原长;v是泊松比;Pi和P0分别为内、外部压力;Ai和A0分别为管道内、外部的横截面面积,对于管道而言,其内部横截面积为0;e为管线阻尼系数,一般忽略不计,在本文中e取为0;dL/ dt是长度增加的速率。
至于弯曲应力、曲率等数值的计算在OrcaFlex中和一般的教科书中都有详细地阐述,这里就不再详述。
2 基于OrcaFlex的模型建立
当牵引的管道下放至海底后,为了能让牵引正常进行需要在连接现场整理出一个清洁区。牵引管为了能够准确拉至漏斗形的出油管端,需由两根拖揽拉向目标。而两根拖揽在模型中用绞车缆绳代替。在管道牵引的过程中,设置了一个类似门的牵引通道。该牵引通道可以帮助管道最终对齐和防止管道在接近出油管端时发生缠绕现象。漏斗形的出油管端也能帮助管道与出油管端顺利对齐。
管线模型的建立基于凝集质量参数法,水流载荷和拖曳力的计算是基于Morison公式;牵引通道、导管架和出油管端用的是OrcaFlex中的弹塑性模块;两个拖揽用的是OrcaFlex中的Winch模块,并对管道进行不同速度的牵引。
根据环境参数及工作条件,在OrcaFlex中建成如图1的模型。

图1 海底管道牵引示意图Fig.1 Schematic model of submarine pipeline towing
3 计算结果及分析
对于海底的管道牵引,一般是不考虑波浪和风载荷作用。所以,只进行不同海流角度下的动力学分析。海流方向从0°开始每隔25°取一个流向,且取的方向是在全局坐标下相对于X轴而言的,具体如图2所示。同时,由牵引通道和牵引管道的坐标得知:管道的牵引角度与X轴大致呈60°~75°。但当管道经过牵引通道后,牵引角度就变为40°~45°左右(牵引的方向皆为X轴负方向)。当管道在模拟牵引的过程中,沿管长方向长度为0 m的点为牵引点A,管道末端为牵引点B。
3.1 不同海流流向下管道各处的水动力分析
3.1.1 不同海流流向下管道各处有效张力的水动力分析
图3是沿缆长方向管道各处有效张力最大值、最小值和平均值的变化情况。从图中可以发现管道有效张力的最大值、最小值和平均值的大小都沿管道长度方向逐渐的减小,但在牵引端A处有效张力会发生急剧地突变。这种突变出现的原因是因为在管道和与拖揽的连接处独立设置了一段牵引端,而该牵引端与管道属于两个不同的非线性弹簧,所以牵引端独自承受了较大的有效张力,减小了有效张力对管道的影响。由于牵引管道的长度较大,只有距管道牵引点A较近的管端才会接触到出油管,而出油管与牵引管端的对接会造成较大的有效张力,这也是管端有效张力较大的一个原因。
观察图发现,当海流方向为50°~175°时,管道各处有效张力最大值会达到23~24 kN,大于其他海流方向产生的有效张力。这是由于管道的牵引方向在40°~75°,而当海流方向为50°~100°时,管道牵引方向与海流的方向相反,即成180°,管道此时会产生较大的轴向的拖曳力阻碍管道的牵引。由于产生了较大的轴向拖曳力,管道的轴向平均应变也随之增大。由壁面张力公式可知,管道的壁面张力和有效张力在轴向应变增大的同时也增大。而当海流方向在125°~175°时,管道牵引方向与海流方向几乎垂直,这就导致了管道横向拖曳力增大,管道的壁面张力和有效张力也随之增大。在海流流向为300°~350°时,管道牵引方向与海流大致呈90°但有效张力却小于海流流向为125°~175°的有效张力。该现象仍需进一步研究。

图3 沿管长方向管道有效张力变化Fig.3 Change of effective tension of pipeline along the length direction
3.1.2 不同海流流向下管道各处曲率与弯曲应力的水动力分析
图4为沿管长方向管道各处曲率最大值、最小值和平均值的变化情况,图5为沿管长方向管道各处曲率最大值、最小值和平均值的变化情况。对比观察两幅图可知,在弯曲应力集中发生突变的地方也是曲率较大、弯曲较严重的地方,曲率和弯曲应力的图像在形态上呈现一定的相似性。从图4和图5中,可以发现在管道距牵引点A 0~25 m、175~300 m和320~400 m这三段会因为海流方向的不同而出现不同的曲率和弯曲应力,其他段落处的管道不会因为海流流向的不同而产生曲率和弯曲应力的差异。在距牵引点A 0~25 m处的曲率和弯曲应力明显大于其他位置,且在牵引点A处曲率最大值为0.125 rad·m-1,弯曲应力最大值为7.4 kPa。当海流流向为150°~175°时,由于海流流向与管道牵引方向大致呈90°,其横向拖曳力达到最大值,曲率和弯曲应力也随之大于其他流向的曲率和弯曲应力。而且由于牵引点A直接受到两根拖揽的牵引,这就导致了牵引点A处的曲率和弯曲应力为各处最大值。在距牵引点A175~300 m和320~400 m的两段为图1中(牵引之前,管道铺设完成的形状)弯曲的两端。距牵引点A175~300 m这段管道在海流流向为325°~0°时,产生的曲率最大值和弯曲应力最大值大于其他海流流向。而另一段弯曲管道则在海流流向为75°~125°时,曲率最大值和弯曲应力最大值会大于在其他流向下的曲率最大值和弯曲应力最大值。出现这种现象的原因是:距牵引点A175~300 m和320~400 m的两个弯曲管段在325°~0°和75°~125°两个方向下由于弯曲角度和海流流向的原因会产生了不同大小的弯曲应力,从而导致管道曲率的不同。
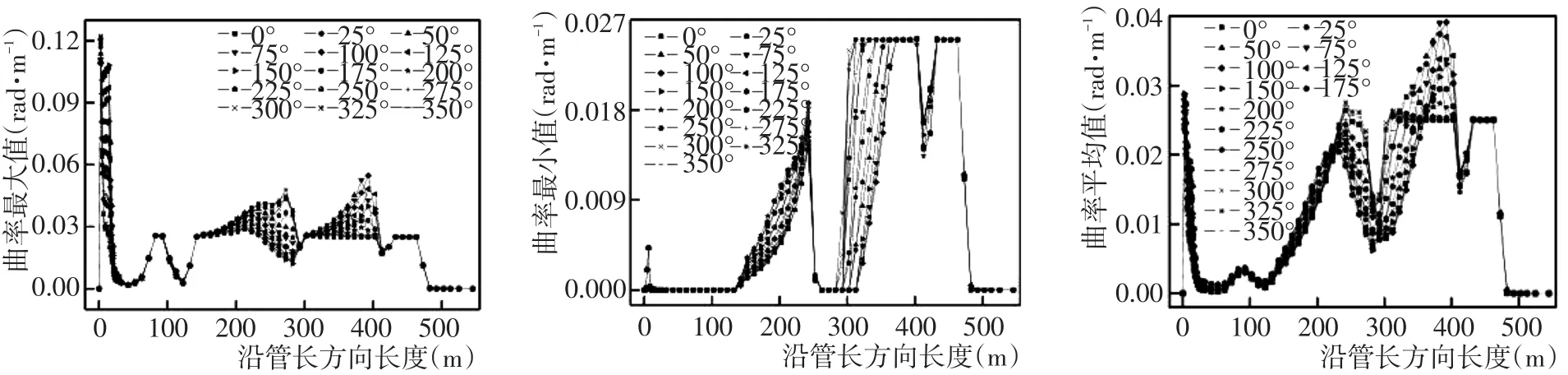
图4 沿管长方向管道曲率变化Fig.4 Change of curvature of pipeline along the length direction
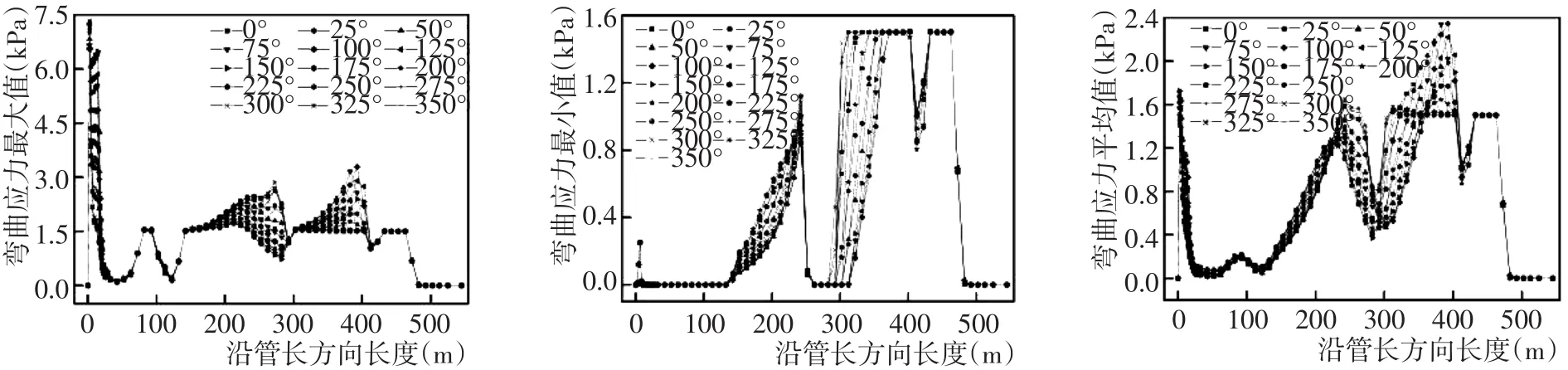
图5 沿管长方向管道弯曲应力变化Fig.5 Change of bending stress of pipeline along the length direction
3.1.3 不同海流流向下管道各处剪力的水动力分析
图6为沿管长方向管道各处剪力最大值、最小值和平均值的变化情况。从图中,可以发现除了距牵引点A 0~25 m的位置,管道最大剪力、最小剪力和平均剪力基本趋近于零,只有小幅度的起伏,但总体变化不大。这种现象表明管道在牵引过程中,除了距牵引点A较近的位置基本不承受剪切应力,而在牵引点A管道的最大剪切应力会达到11 kN。这是由于管道的牵引点A在牵引通道和出油管段处受到一定的轴向牵引力和摩擦力,从而产生较大的剪切应力。这个出现应力突变的位置十分容易出现应力集中现象,所以在牵引点A处应事先做好防护措施。观察图(6)可以发现,在不同海流流向作用下,距牵引点A 0~25 m的管段的最大剪切应力有明显的不同。当海流流向在125°~175°之间时,由于海流产生的拖曳力的影响管道的最大剪切应力会大于其他流向下的管道的最大剪切应力,但皆远小于牵引点A处的最大剪切应力。
3.1.4 不同海流流向下管道各处von mises应力的水动力分析
图7为沿管长方向管道各处von mises应力最大值、最小值和平均值的变化情况。由图可知von mises应力最大值、最小值和平均值在距牵引点A 2 m处发生明显的突变。这是由于距牵引点0~2 m的牵引端的外径为0.3 m,而这外径要大于牵引管道外径。通过改变牵引端外径的大小,可以发现外径的增大有效降低了von mises应力。同时对比有效张力最大值与von mises应力最大值,可以发现除了在距牵引点A0~2 m处两者有着显著地不同,而其余各处在不同海流流向下的变化趋势十分地接近。这在一定程度上说明了管道牵引过程中von mises应力与有效张力紧密相关。API 2RD允许的许用应力为240 000 kPa,在牵引过程中的von mises应力远小于该值,可满足工程要求。

图6 沿管长方向管道剪力变化Fig.6 Change of shear force of pipeline along the length direction
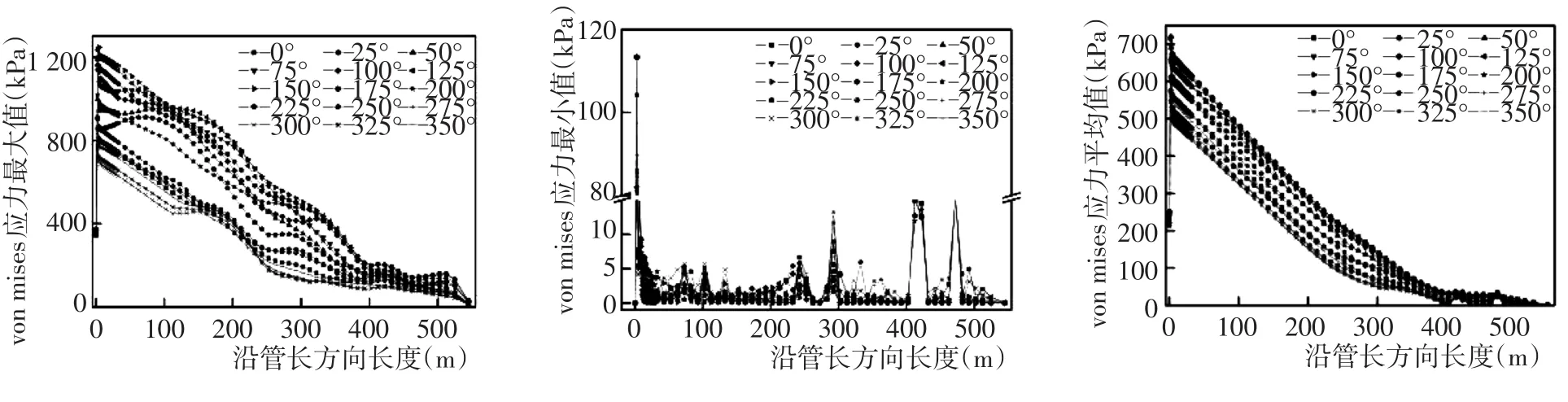
图7 沿管长方向管道von mises应力变化Fig.7 Change of von mises stress of pipeline along the length direction
3.2 不同海流流向下管道牵引点处的时域水动力分析
由上面的水动力分析可以得知:管道的牵引点A在牵引过程中受到的有效张力、剪切应力等要大于管道其余个处,所以本文将选取牵引点A进行时域水动力分析。
3.2.1 不同海流流向下管道牵引点A处有效张力的时域水动力分析
图8为不同海流流向下管道牵引点A处有效张力随时间变化的情况。从图中可以发现牵引点A在海流流向为75°~150°会有更大的有效张力,而这个现象与上文现象相似且已经做过解释,这里就不做过多地赘述。观察图(8)不难发现,牵引点A由于拖揽将其从静止状态拖动有效张力也在0~12 s时快速增大达到17.5 kN。当牵引时间到达46 s时,牵引点A的有效张力发生了急剧地突变,直到降到0 kN。此时,结合OrcaFlex模拟的牵引过程,可以得知在有效张力为零的时间段内,牵引点A正好到达了为对齐出油管而设置的牵引通道。为了能够使管道与出油管安全对接,牵引点A在牵引通道处所受牵引力急剧地减小,牵引速度也急剧减小,甚至在一段时间内为零。这就不难解释有效张力在46 s发生突变了。在经过牵引通道后,由于牵引力的减小,有效张力也一定程度地降低了。但在70 s处,牵引点A的有效张力急剧地增加到了22~23 kN。而此时的有效张力为牵引点A在牵引过程中所承受的最大有效张力。同样,通过Or⁃caFlex模拟的牵引过程,可以得知此时为管道与出油管开始对接的时间段。在对接过程中,牵引点会与漏斗形的出油管口发生一定程度地碰撞,从而导致牵引点A处有效张力的增大。

图8 牵引点A有效张力随时间变化Fig.8 Effective tension of towing point A changing with time

图9 牵引点A剪力随时间变化Fig.9 Shear force of towing point A changing with time
3.2.2 不同海流流向下管道牵引点A处剪力的时域水动力分析
图9为不同海流流向下管道牵引点A处剪切应力随时间变化的情况。从图中可以发现牵引点A的剪切应力由于其自身的移动产生了较大的剪切应力。但当牵引速度稳定时,剪切应力就降至0.8 kN,且在不同海流流向下剪切应力的变化不大。当牵引时间到达46 s,即牵引点A到达牵引通道处,剪切应力发生了与开始牵引时相同的现象。当牵引时间到达72 s后,牵引点A刚进入出油管,其速度逐渐降至0 m/s,从而导致剪力急剧地减小至0 kN。但80 s后,牵引点A剪切应力的急剧增加的现象需通过对对接过程作进一步的分析才能解释其原因。
4 结论
(1)不同海流流向下,管道在牵引过程中的有效张力、曲率、弯曲应力和von mises应力的大小会有一定程度的不同。当海流流向与管道牵引方向呈90°或180°(两者方向相反)左右时,管道产生的有效张力、曲率、弯曲应力和von mises应力会大于其余流向下的有效张力、曲率、弯曲应力和von mises应力。所以应在进行管道牵引时,极力避免牵引方向与海流流向呈90°或180°。
(2)管道牵引端的有效张力、曲率、弯曲应力和剪力值是整根管道中最大的,其余各处的有效张力、曲率、弯曲应力和剪力值会沿着管长方向减小。剪切应力甚至只在管道牵引端产生,而在其余各处几乎为0。
(3)由于海流的存在,管道在牵引之前的铺设形状会对牵引过程中产生的有效张力、曲率和弯曲应力造成一定的影响。下放至海底的管道应避免与海流呈90°。在牵引之前管道应避免因海流或下放不当而造成过大的弯曲,而对之后的牵引造成影响。
(4)在管道牵引过程,有效张力的大小会一定程度地决定von mises应力的大小。当其余条件相同的情况下,管道在牵引过程中有效张力越大,其von mises应力也越大。为了避免管道牵引端的von mises应力过大而发生管道弯曲和扭转等现象,可以通过加大牵引端的外径来有效减小von mises应力。
(5)当管道处于牵引通道和出油管处这两个位置时,由于拖揽拖曳力的改变,管道的有效张力和剪切应力出现明显的突变。该突变一般是有效张力和剪切应力先急剧地减小到零,随后急剧地增加到最大值,从而出现的应力集中现象。所以在工程上,当管道牵引至牵引通道和出油管时应做好监测工作,避免发生牵引事故。
[1]Lenci S,Callegan M.Simple Anatical models for the J⁃lay problem[J].Acta Mechanica,2005,178(1-2):23-39.
[2]张大朋,朱克强,荆彪,等.文昌脐带缆J型牵拉入位操作的水动力分析[J].船舶工程,2015,37(4):92-97. ZHANG D P,ZHU K Q,JING B,et al.Hydrodynamic analysis of mooring system for wenchang umbilical cable J⁃tube pull⁃in instal⁃lation[J].Ship Engineering,2015,37(4):247-252.
[3]陈凯,段梦兰,张文.深水S型铺管管道形态及力学分析方法研究[J].力学季刊,2011,32(3):353-359. CHEN K,DUAN M L,ZHANG W.On configuration and mechanical analysis method for deepwater S⁃lay subsea pipeline[J].Chi⁃nese Quarterly of Mechanics,2011,32(3):353-359.
[4]伊才颖,王琮,赵东岩.深水海底管道铺设托管架模型试验研究[J].水道港口,2012,33(2):173-177. YI C Y,WANG C,ZHAO D Y.Research on model test of stinger applied in deepwater pipeline laying[J].Journal of Waterway and Harbor,2012,33(2):173-177.
[5]黄玉盈,王忠民,杨挺青.海洋管线在有摩擦的弹性地基上铺设时的大变形分析[J].应用力学学报,1988,5(4):110-118. HUANG Y Y,WANG Z M,YANG T Q.Large deflection analysis of submarine pipelines with elastic foundation during installation[J].Chinese Journal of Applied Mechanics,1988,5(4):109-118.
[6]梁振庭.深水海底管道铺设受力性能分析[D].浙江:浙江大学建筑工程学院,2008.
[7]李旭.海底管线牵引技术分析与程序开发[D].天津天津大学建筑工程学院,2007.
[8]唐立志,张若瑜,唐友刚,等.滩海水域铺管海底牵引管道受力分析及拖带方式研究[J].石油工程建设,2006,32(6):31-33. TANG L Z,ZHANG R Y,TANG Y G,et al.Study on technology of towing pipeline on sea bottom for laying pipeline in extreme shallow water[J].Petroleum Engineering Construction,2006,32(6):31-33.
[9]白勇,白强.海洋工程设计手册:海底管道分册[M].上海:上海交通大学出版社,2014.
Dynamic response in the process of submarine pipeline towing under different current directions
ZHAO Wang⁃qi1,ZHU Ke⁃qiang*1,ZHANG Da⁃peng1,WANG Zi⁃fa2
(1.Faculty of Maritime and Transportation,Ningbo University,Ningbo 315211,China;2.COOEC International Engineering CO.,LTD.,Tianjin 300456,China)
Based on the relevant papers of submarine pipeline towing,combined with the specific process of pipeline lateral pull,the simplified model of submarine pipeline towing has been established by OrcaFlex.With the change of the current direction,the extent of influence on the pipeline towing under different current directions and the optimum current direction for pipeline towing were gotten.At the same time,in the time domain hydrodynamic analysis of the traction point A,the stress concentration phenomenon occurred easily when the pipeline was passing through the traction passage and the oil pipeline.According to the calculated results,the relevant motion perfor⁃mance and the attention items of submarine pipeline towing were obtained.
pipeline towing;OrcaFlex;hydrodynamic analysis;different current directions
TV 134
A
1005-8443(2017)02-0181-07
2016-06-14;
2016-08-12
国家自然科学基金资助项目(11272160)
赵望奇(1992-),男,浙江湖州人,硕士研究生,主要从事船舶与海洋工程物结构响应研究。
*通讯作者:朱克强(1956-),男,教授,博士生导师,主要从事船舶与海洋工程物结构响应研究。E⁃mail:zhukeqiang@nbu.edu.cn.
Biography:ZHAO Wang⁃qi(1992-),male,master student.

