基于VOF的物体入水-下潜过程数值模拟

王 平，袁 帅，邹文峰，陈伟斌，史文奇

（1.国家海洋环境监测中心，大连116023；2.大连中交理工交通技术研究院，大连116024）

基于VOF的物体入水-下潜过程数值模拟

王 平1，袁 帅1，邹文峰2，陈伟斌1，史文奇1

（1.国家海洋环境监测中心，大连116023；2.大连中交理工交通技术研究院，大连116024）

漂浮物体在取水口附近入水后可能会下潜至涵道，为数值研究其入水-下潜过程，基于计算流体力学模型中的VOF法，并结合动网格方法，首先构建了不同密度圆柱体的自由入水以及出水过程，验证了物体出入水过程造成的射流、入水深度及物体速度变化；其次结合二维明渠的取水过程模拟了不同初始动量条件下圆柱体的入水-下潜过程。结果表明：文章建立的入水-出水数值模型可很好地刻画二维圆柱体入水及出水的具体过程，且初始动量大小是圆柱体在入水后能否下潜至取水涵道的关键因素，数值结果为判断取水口附近物体入水后的下潜风险提供了分析依据。

物体入水；下潜；VOF；取水明渠；数值模拟

取水过程是沿海附近电厂包括核电厂冷却水循环的关键步骤，但在取水过程中可能会出现附近漂浮物（如海冰）下潜进入至取水口涵道，进而影响电厂运营的安全。随着计算机的发展，数值模拟物体出入水等问题已越来越成熟，因而采用数值方法研究取水口附近的物体下潜问题已成为可能，其对核电厂取水及运营安全至关重要。

数值计算物体下潜过程的研究较少，与之相近的有隋觉义［1］总结并分析了冰盖前缘处的冰块下潜临界条件，练继建等［2］采用VOF模型模拟了渠道冰凌下潜过程，其主要从受力角度分析，并未计算固体的运动过程。而数值模拟物体入水的研究较多，如Zhao［3］以及Zhu［4］基于势流理论假设采用边界元方法研究了楔形体的入水问题，但无法刻画入水过程造成的射流影响；Shao［5］采用了无网格的SPH法计算了物体入水中的自由液面及流固相互作用等问题，很好地处理了入水时液面变形较大问题，但数值计算量较大；Gu［6］采用level set法捕捉自由水面，并模拟了固体在垂向及倾斜入水时的变化过程；Arai［7］采用带自由表面的两相流模拟方法（VOF）模拟了二维楔、圆柱船艏的砰击入水问题，陈宇翔［8］采用了VOF方法对圆柱的入水过程进行了模拟，胡子俊［9］采用基于CIP的VOF法模拟了不同密度圆柱体的入水过程，方舟华［10］则采用该方法模拟了圆柱体入水和出水的整个过程，结果表明：VOF法可以很好地处理自由面重构等强非线性现象。

密度小于水的漂浮物受取水过程的影响一般会聚集在取水口附近水面，但当具有一定的初始动量的情况下，则会发生入水过程，在其入水深度达到一定位置时，则会在取水流速的影响下进入取水涵道，进而造成涵道的堵塞及取水效率的降低。本文基于计算流体力学模型，首先构建了不同密度圆柱体的自由入水及出水过程，研究了物体入水过程造成的射流、入水深度及物体速度变化等；其次模拟了二维明渠的取水过程；最后结合二维明渠取水及圆柱体入水过程模拟了不同密度圆柱体在不同初始动量条件下的下潜过程。该计算过程为研究取水口物体下潜的可能性提供了一种数值方法，同时数值结果也为判断取水口附近物体下潜风险提供了分析依据。

1 数值模型

对于不可压缩流体，在直角坐标系下其运动规律可以用N-S方程来描述，包括连续性和动量方程分别为

式中：uj为(x,y,z)3个方向上的流速分量；Fi为单位质量力沿(x,y,z)3个方向的分量；P为压强；υt为紊流粘性系数，本文采用k-ε湍流闭合模型对其求解。

自由面追踪采用VOF法，即通过求解单独的动量方程和处理穿过区域的每一流体容积比来模拟两种或多种不能混合的流体。定义体积函数αq代表第q种流体，对任一单元存在3种可能，即：αq=0表示该单元第q流体不存在；αq=1表示该单元充满第q流体；0＜αq＜1表示该单元存在着流体之间的界面。

以第q流态为例，其体积函数的输移扩散方程

在任一单元中控制方程的特性参数是由几种流体的组合表示，以q1和q2两种流态为例，那么单元体的密度可以表示为式（4），其他特性参数如粘性系数等均按此方法计算。

对由固体运动造成的动边界问题则采用动网格技术，即完成每一步物体的运动状态计算后重新划分网格。为详细刻画物体入水时的射流现象在物体周围设置移动加密网格，该计算域网格随物体一起下移。而物体的运动则使用6自由度模型计算，并通过自定义函数定义其质量及转动惯量等。

数值计算中采用Piso算法耦合速度和压力场，VOF模型采用自由面重构方法来处理液面变化，湍流采用k-ε两方程模型和壁面函数法；由于物体入水过程中受到较大的体积力，压强计算采用体积力加权（Body Force Weighted）的二阶差分格式；密度和动量均采用二阶迎风格式。iq=1

2 物体入水模拟

圆柱入水是研究入水问题的典型算例，在圆柱入水的瞬间，圆柱的速度突然下降，并改变了周围压力等流场参数，而与其接触的水会被突然加速，并在圆柱两侧激起两股射流，射流斜向上上升并逐渐变得不稳定，并在重力作用下逐渐向下弯曲，最终融入水中。若圆柱密度小于水体，圆柱入水后速度逐渐减小，并在达到一定深度后在浮力的作用下逐渐上升，随后完成一次出水过程。以下则利用数值方法刻画圆柱入水及出水的具体过程。

根据Greenhow［11］的实验设计圆柱体的直径为11 cm，圆柱体的密度分别为零浮力（密度与水相同）和半浮力（密度为水的一半），实验中圆柱由静水上方0.5 m处自由下落，忽略空气阻力，在圆柱接触自由水面时速度为2.955 m/s。数值计算中初始时刻为圆柱体刚接触自由水面，圆柱初始速度设置为2.955 m/s；计算域选取为1.5 m×1 m的水槽，水槽的上边界为气体压力出口，水槽左右两侧均为水体压力出口，并设定为固定压力梯度，以减少入水时水位上升带来的影响，水槽底端为固边界；计算网格采用三角形网格，网格尺寸在0.35～1.5 cm间变化，圆柱体边缘采用和圆柱体一起移动的四边形网格（图1），计算时间步长为2× 10-4s。

图1 圆柱入水初始时刻的计算网格Fig.1 Numerical grid for the circular cylinder water⁃entry case

数值计算得到零浮力圆柱体在开始下落后0.015 s、0.03 s、0.04 s和0.2 s时以及半浮力圆柱体在开始下落后0.02 s、0.035 s、0.045 s和0.085 s时的自由面变化以及其和实验结果的对比见图2和图3。从图中可知本文基于CFD模型所建立的二维圆柱体入水模型很好地模拟了圆柱入水后所引起的射流形成和发展过程，同时数值计算得到两种浮力圆柱体入水后的深度变化与实验对比见图4，除个别点异常外，整体结果吻合较好。

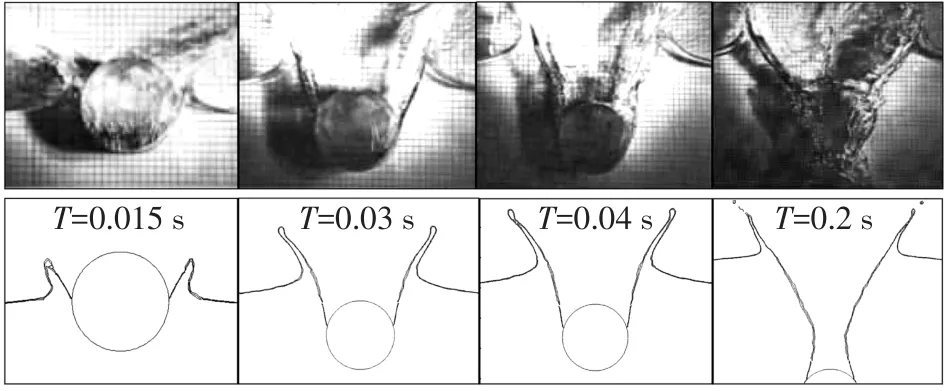
图2 零浮力圆柱体入水时自由面变化与实验的对比Fig.2 Free surface deformation of a neutrally buoyant cylinder water⁃entry

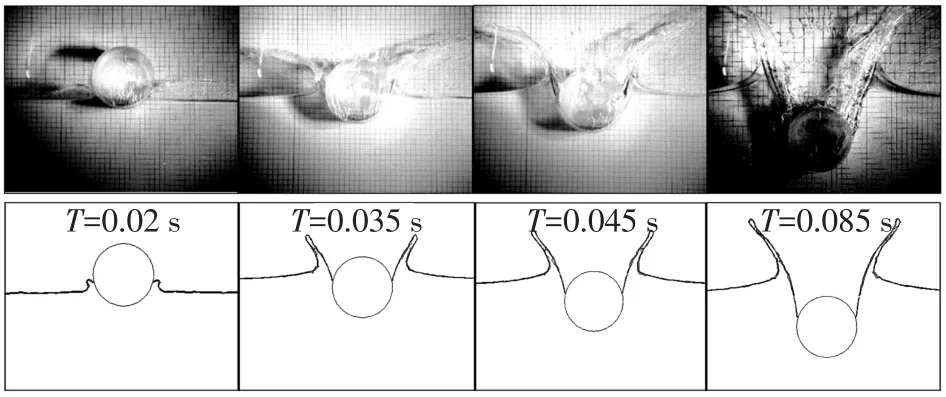
图3 半浮力圆柱体入水时自由面变化与实验的对比Fig.3 Free surface deformation of a half buoyant cylinder water⁃entry

图4 两种浮力圆柱体的入水深度与实测值对比Fig.4 Comparison of cylinder underwater depth between simualtion and measurement

为研究物体自由入水和出水的整体过程，Colocchio等［12］在实验水槽中距水面0.48 m释放一直径为0.3 m的不锈钢圆柱，圆柱与水体密度之比为0.62，由于浮力作用，圆柱经历了入水和出水两个过程。数值计算初始时刻圆柱体底部接触水体，根据实验结果初始速度设为2.55 m/s。数值网格在0.1～2 cm之间变化，时间步长为2×10-4s。

构建上述类似的数值水槽，计算域选取为2 m×1.5 m，水槽上边界为气体压力出口，水槽左右两侧同样均为水体压力出口，并设定为固定压力梯度，水槽底端为固边界。数值计算得到圆柱体底部竖向坐标和圆柱竖向速度随时间变化以及实测值（图5），从图可以看出本文建立的圆柱体入水模型与实验数据吻合较好，圆柱体经历了一个明显的下降、上浮和再下降的过程。

同时给出几个典型时刻圆柱体周边的速度场分布（图6），0.4 s左右圆柱体开始浸没在水中，同时伴随着速度很大的顶部射流出现，0.575 s左右射流达到最大高度并开始下落，1.175 s左右柱体则完全浮出水面，此时圆柱体完成了一个完整的入水-出水过程，数值计算的结果和实验时间基本一致。

图5 圆柱体底部高度和垂向速度变化及和实测值对比Fig.5 Comparison of cylinder bottom height and vertical velocity between simulation and measurement

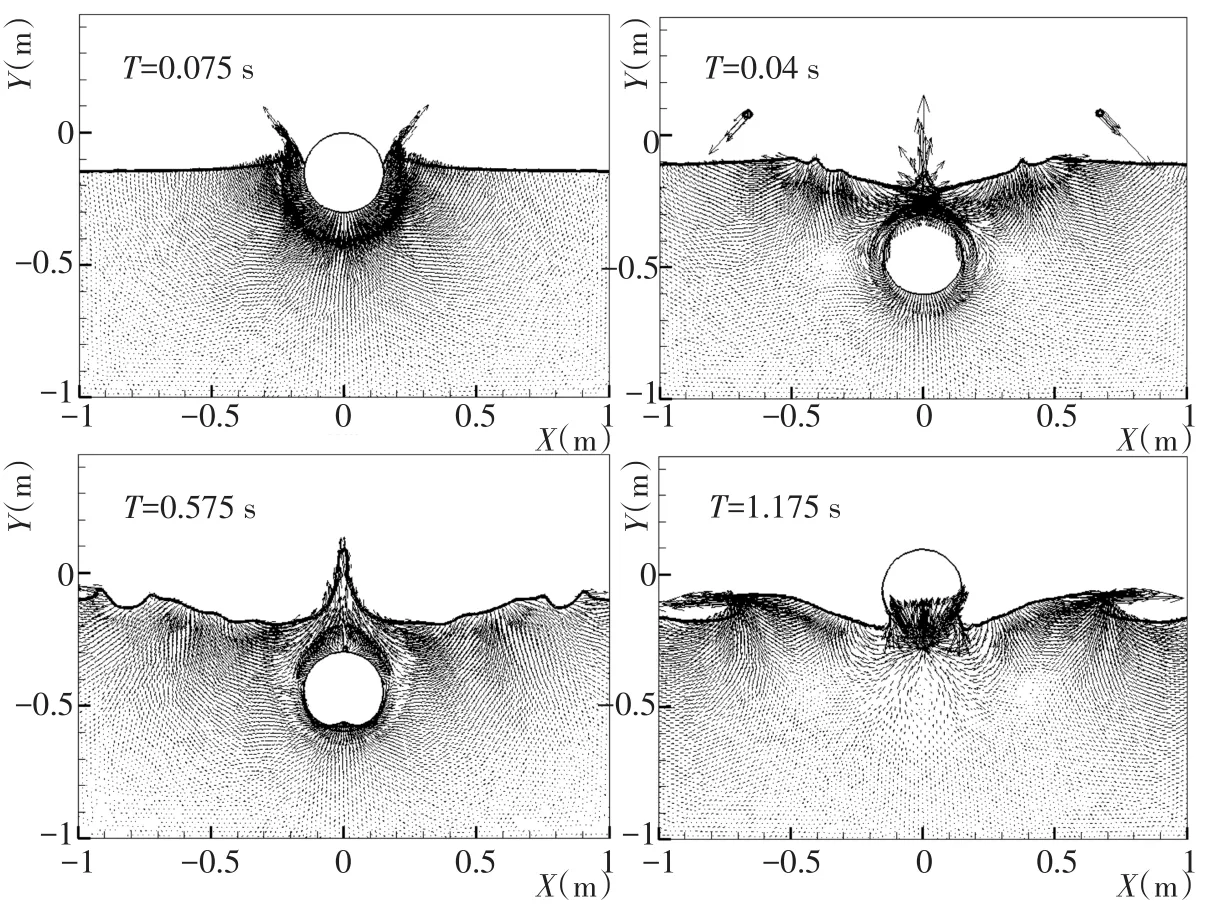
图6 圆柱体入水时不同时间的周围速度场分布Fig.6 Velocity distribution for cylinder water⁃entry at various water entry moments

3 物体下潜模拟

取水过程会导致取水口附近存在明显的垂向流速，对于密度接近于水的物体在取水口附近会存在直接下潜的风险，而对密度稍小于水的物体其入水过程，并不像在静止水槽中那样（圆柱在下潜到一定深度后发生上浮并完成出水），而是在下潜到一定深度后会受取水流速的影响直接潜入至取水廊道中。以下则利用入水及取水模型数值研究密度小于水的圆柱在入水后的可能下潜过程。

为获得取水口附近物体发生下潜的可能性，首先构建一个二维取水的数值水槽（图7），水槽尺度19 m×8 m，其中取水涵道距水底1 m，涵道高3 m，为简化计算涵道长度为3 m。水槽左侧为压力入水，计算时设定为固定压力梯度，即水位保持固定在6 m；水槽右端为速度出口，计算时设定为稳定流量2.4 m3/s；水槽内水面高度为6 m，上边界为气体的压力出口；圆柱体直径为0.3 m，初始位置设置在（x=13.5 m，y= 6.15 m）处，圆柱体与水体密度之比为0.92。

数值计算初始阶段圆柱体固定不动，只计算水槽内的流场变化。由于明渠内的水体由静止开始计算，初期的自由液面会有一定的波动，随着取水的进行，波动逐渐减小并将趋于稳定，图8给出了x=14 m处自由液面随时间的变化，从图可知在单独计算明渠取水1 000 s左右后，水槽内的水面基本保持不变，此时开始计算圆柱体的入水过程。

图9给出了圆柱体开始入水时取水明渠内的流速矢量分布，从图中可知，受取水影响取水口附近水体存在明显的垂向流速，其将决定圆柱体是否会潜入涵道。忽略空气影响，考虑两种工况，工况1：假设圆柱从距水面0.8 m的高度下落，圆柱体接触水面时的速度约4 m/s；工况2：假设圆柱从距水面0.45 m的高度下落，圆柱体接触水面时的速度约3 m/s，数值计算均从圆柱体接触自由液面开始。

数值计算在圆柱体与固边界发生碰撞溢出后停止，计算得到工况1条件下圆柱体的入水-下潜过程，见图10-a，图中给出了入水后每隔0.5 s圆柱体的位置变化，以及入水开始时明渠内的液面及流线图；工况2中圆柱体在入水5 s后与取水口前壁发生碰撞，此时数值计算停止，图10-b给出了此刻明渠内的液面及流线图，以及入水后每隔0.5 s的圆柱体位置变化。

从图10可知，工况1条件下的圆柱体在入水后下潜至取水涵道内，而工况2由于与取水口前壁碰撞并未直接潜入取水涵道，因为初始条件的不同，两种工况下圆柱体的入水路径有所区别，且工况1圆柱体潜入涵道的时间要短于工况2，说明工况1条件下的圆柱体在入水后更易发生下潜。

图7 二维取水明渠及圆柱体下潜计算示意Fig.7 Calculation sketch of two⁃dimensional water channel and cylinder dive

图8 明渠取水计算时x=14 m处的水位变化Fig.8 Surface change inx=14 m of open channel

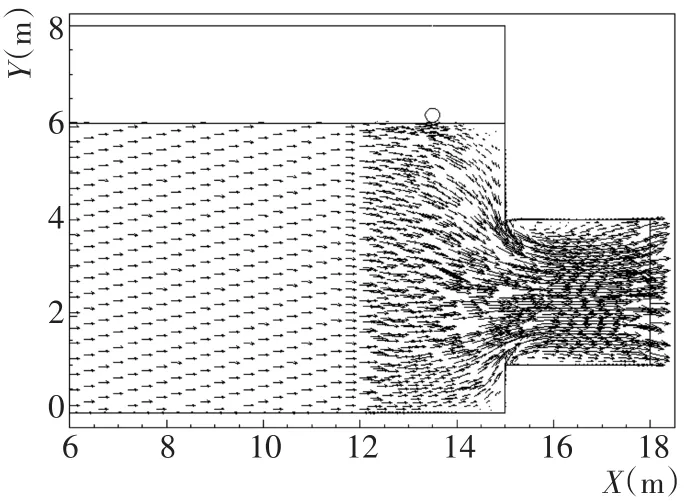
图9 圆柱体开始入水时的取水明渠内的流场分布Fig.9 Velocity distribution of open channel at water entry moment

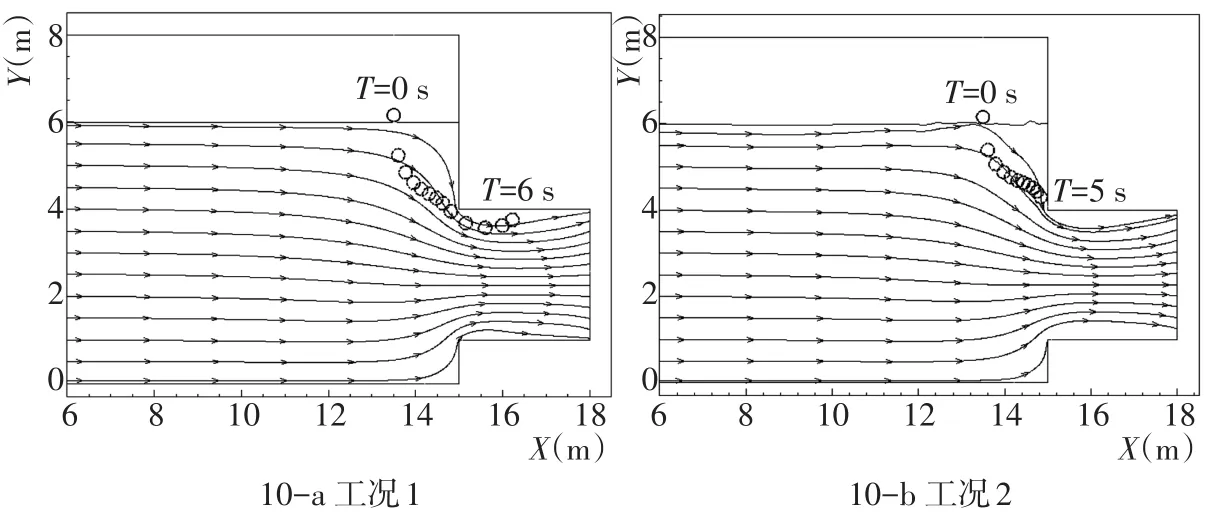
图10 两种工况下圆柱体的入水-下潜过程Fig.10 Cylinder water entry and dive process of two cases simulated by present model

为对比取水对圆柱体下潜过程的影响，同时模拟了在没有取水（静水）时，工况1和2条件下的圆柱体入水-出水过程，数值得到工况1、工况2及其静水条件下圆柱体的入水深度和y向速度变化对比如图11。从图可知，工况1（静水）时，圆柱体在入水3 s后开始上浮，而在受到取水流速的影响后，圆柱体则会继续向下移动，并在4 s后潜入涵道，其y向速度值也在3 s后不断增加并在潜入至涵道后逐渐减小；工况2（静水）条件下，圆柱在入水2.5 s后开始上浮，而受取水影响后，圆柱体的下潜深度及y向速度在入水4 s后均逐渐增大，并在入水后5 s时与取水口前壁发生碰撞。

图11 不同情况下圆柱体的入水深度及y向速度变化对比Fig.11 Comparison of cylinder bottom height and vertical velocity between different cases

4 结论

为数值研究取水口附近物体下潜的可能性，基于计算流体力学模型中的VOF法，并结合动网格方法构建了不同密度圆柱体的自由入水及出水过程，验证了物体入水过程造成的射流、入水深度及物体速度变化等；其次模拟了二维明渠的取水过程；最后结合二维明渠取水及圆柱体入水模拟了不同初始动量条件下圆柱体的入水-下潜过程。

数值计算结果表明：本文建立的入水-出水模型可很好地模拟二维圆柱体入水及出水形成的射流及速度变化，且初始动量大小决定了圆柱体在入水后是否能下潜至取水涵道，该计算过程为研究取水口附近物体入水后的下潜可能性提供了一种数值方法。由于计算量的限制，本文并未考虑三维实际情况，后续研究应予以关注。

［1］隋觉义，方达宪.冰盖前缘处冰块下潜临界条件研究［J］.水利学报，1993（8）：10-18. SUI J Y，FANG D X.Study on the critical condition of ice dive in ice cover leading edge［J］.Journal of Hydraulic Engineering，1993（8）：10-18.

［2］练继建，罗昉昕，赵新.渠道冰凌下潜的数值模拟研究［J］.水利学报，2013，44（6）：673-679. LIAN J J，LUO F X，ZHAO X.Numerical simulation of ice submergence in water conveyance channel［J］.Journal of Hydraulic En⁃gineering，2013，44（6）：673-679.

［3］Zhao R，Faltinsen O M.Water⁃entry of two⁃dimensional bodies［J］.Journal of Fluid Mechanics，1993，246：593-612.

［4］Zhu X Y，Faltinsen O M，Hu C H.Water entry and exit of a horizontal circular cylinder［J］.Journal of Offshore Mechanics and Arc⁃tic Engineering，2007，129：253-264.

［5］Shao S D.Incompressible SPH simulation of water entry of a free⁃falling object［J］.Int.J.Numer.Meth.Fluids，2009，59：91-115.

［6］Gu H B，Qian L，Causon D M，et al.Numerical simulation of water impact of solid bodies with vertical and oblique entries［J］. Ocean engineering，2013，75（5）：128-137.

［7］Arai M，Chen L Y，Inoue Y.A computing method for the analysis of water impact of arbitrary shaped bodies［J］.Journal of Computa⁃tional Physics，1981，39：201-225.

［8］陈宇翔，郜冶，刘乾坤.应用VOF方法的水平圆柱入水数值模拟［J］.哈尔滨工程大学学报，2011，11（32）：1 439-1 442. CHEN Y X，GAO Y，LIU Q K.Numerical simulation of water⁃entry in a horizontal circular cylinder using the volume of fluid（VOF）method［J］.Journal of Harbin Engineering University，2011，11（32）：1 439-1 442.

［9］胡子俊，叶洲腾，赵西增，等.基于CIP方法的水平圆柱入水数值模拟［C］//左其华，窦希萍.第17届中国海洋（岸）工程学术讨论会论文集.南宁：海洋出版社，2015：117-181.

［10］方舟华，赵西增.物体入水的CIP方法模拟［C］//左其华，窦希萍.第17届中国海洋（岸）工程学术讨论会论文集.南宁：海洋出版社，2015：289-294.

［11］Greenhow M，Lin W M.Nonlinear⁃free surface effects：experiments and theory［R］.Cambridge：Massachusetts Inst of Tech Cam⁃bridge Dept of Ocean Engineering，1983.

［12］Colicchio G，Greco M，Miozzi M，et al.Experimental and numerical investigation of the water⁃entry and water⁃exit of a circular cyl⁃inder［C］//Proceedings of the 24th Int.Workshop on Water Waves and Floating Bodies.Zelenogorsk，Russia，2009：19-22.

Numerical method and study of the body water⁃entry and dive based on VOF

WANG Ping1,YUAN Shuai1,ZOU Wen⁃feng2,CHEN Wei⁃bin1,SHI Wen⁃qi1
（1.National Marine Environmental Monitoring Center,Dalian 116023,China;2.CCCC&DLUT Institute of Transportation Technology Co.Ltd.,Dalian 116024,China）

The body would dive into duct near water intake when it was entering into the water.To numerically study the body water⁃entry and dive,combined the volume of fluid(VOF)method with dynamic mesh,the cylinder water⁃entry and water⁃out with different density was simulated by the Fluent module.The free surface deformation, bottom height and vertical velocity caused by cylinder water⁃entry and water⁃out were verified.The cases of cylinder water⁃entry and dive into water intake with different initial momentum conditions were researched in case of water⁃entry and water⁃out combining with two⁃dimensional water channel.Numerical results show that the specific pro⁃cess of cylinder water⁃entry and water⁃out could be simulated accurately by the module,and initial momentum is the key factor on the cylinder diving into duct after entering into the water.Numerical results provide the analysis basis for judging whether the body dives into water intake.

water⁃entry;dive;the volume of fluid(VOF)method;water channel;numerical simulation

TV 131；O 242.1

A

1005-8443（2017）02-0120-06

2016-09-19；

2016-10-25

海洋公益性行业科研专项（200905007；201505019）

王平（1988-），男，安徽省人，助理研究员，主要从事近岸动力学研究。

Biography：WANG Ping（1988-），male，assistant professor.