感潮河段单站等时距水位非线性优化预报模型

王如云，李 丹，周 钧，汪 天

（1.河海大学海洋学院，南京210098；2.河海大学港口海岸与近海工程学院，南京210098；3.河海大学水文水资源学院，南京210098）

感潮河段单站等时距水位非线性优化预报模型

王如云1，李 丹2，周 钧3，汪 天2

（1.河海大学海洋学院，南京210098；2.河海大学港口海岸与近海工程学院，南京210098；3.河海大学水文水资源学院，南京210098）

目前感潮河段水位预报模型基于当前站水位、上游径流水位和下游海洋潮位数据进行预报，导致预见期受上游来流时间制约、上下游站数据缺失情况下无法进行预报、数据采集成本高等问题。文章假设感潮河段水位由径流因素和潮汐因素共同线性作用，基于单站等时距水位数据，建立了包含一个径流动力修正系数和若干个潮汐调和分潮系数的非线性优化预报模型，并结合曲线拟合最小二乘法、潮汐调和分析法、梯度下降法，给出一个寻优的迭代算法，对模型参数进行优化辨识。模型应用于长江感潮河段部分观测站，水位预报精度较好，具有可行性和实用价值。

等时距；感潮河段；潮汐调和分析；非线性优化预报模型

感潮河段是指河流下游潮区界至河口之间的河段。与上游河段不同，感潮河段受到上游径流和下游潮汐共同作用，水位预报工作较为困难。

目前感潮河段水位预报的方法有很多，根据预报前对水位数据处理方法的不同，可将其分为两种类型，第一类是直接对水位进行预报，主要利用水动力模型［1-2］、概率统计方法［3］及神经网络模型［4-5］等完成预报。第二类则是将感潮河段水位进行潮、洪分离后分别对径流水位和天文潮水位进行预报校准。

针对感潮河段水位的复杂性，将感潮河段水位进行潮、洪分离后处理不失为一个好方法。早在1989年，陈尚渭等人［6］就提出感潮河段水位是上游径流和海洋潮波的复合。2003年，黄国如、芮孝芳［7］将径流和天文潮水位分离研究，提出了建立感潮河段水位与上游径流、下游天文潮因素之间的线性关系，采用频率组合法预报感潮河段的设计洪水位。2013年，Smith等［8］将苏格兰迪河感潮河段水位进行潮、洪分离，对迪河两年的天文潮水位数据进行潮汐调和分析，并与非线性预报的径流水位进行耦合，利用若干站点数据进行逐次修正完成预报。

此外，潮汐调和分析方法在感潮河段水位预报方面的应用也十分广泛。20世纪80年代，陈尚渭等［6］根据长江上游水位及流量数据、下游天文潮特征，提出时间序列分析与潮汐调和分析相结合的方法进行潮位预报。1985年，Speer等［9］指出了感潮河段中，天文潮与径流的相互作用、河床的摩擦、河道不断变化的几何形态存在非线性关系，直接影响了感潮河段的水位。1999年，Godin［10］证明在Saint Lawrence河段可以用河流流量及潮汐分潮的振幅、潮差来预报上游站的水位，并对潮汐调和常数的变化进行校准，进一步指出径流流量与潮汐调和常数之间的变化关系。2010年，Nidzieko［11］发现了感潮河段在涨潮和退潮过程中存在不对称现象，直接导致了感潮河段高低潮（极值水位）出现的时间和潮位不规律。2013年，Li Guofang等［12］利用调和分析方法，构建了长江感潮河段潮位预报模型，同时通过对实测潮位的预报，得到了预报误差与径流之间存在的关系，建立了以大通水文站实测流量为输入数据的实时校正模型。同年，Moftakhari等［13］通过连续32 d的潮汐数据进行调和分析，通过得到的参数对旧金山潮汐数据以及萨克拉门托河的水位流量数据进行校正，较为准确地反应了该感潮河段的水位及流量状况。

目前的感潮河段站位的水位预报方法基本都基于对上游径流水位观测站、下游海洋潮位站，以及当前感潮河段站位的水位观测资料的分析，建立预报模型。然而该方法存在如下问题：（1）预见期受上游来流时间制约；（2）如果出现上下游站位数据缺失，预报将无法进行；（3）为了对感潮河段的水位进行预报，除了建立当前观测站外，还必须在其上游和下游分别建立径流水位和海洋潮位观测站，势必增加很大费用。为了克服这些问题，建立了只需要当前站水位的数据进行水位预报的非线性数学模型，其基本思想是，在假设感潮河段水位由径流因素和潮汐因素共同线性作用引起的情况下，通过考虑对径流采用一个带动力修正项的水位预报模型，对潮汐采用调和分潮和函数的潮位预报模型情况下，基于曲线拟合最小二乘法，建立了关于一个动力修正系数和若干个分潮调和系数的非线性目标函数，并结合调和分析法、梯度下降法，给出了一个寻优的迭代算法，对模型参数进行优化辨识。经过对长江感潮河段一些观测站水位进行预报检验，结果表明预报精度较好，具有可行性和实用价值。

1 感潮河段单站等时距水位非线性优化预报模型

假设感潮河段某水位观测站等间距时刻ti的水位为ηi

式中：η(t)为感潮河段水位。

由于感潮河段水位受上游径流和下游天文潮共同作用，所以假设感潮河段水位可分离为径流水位和天文潮水位之和，即有

这里η¯(t)为径流水位，η~(t)为天文潮水位。

假设径流水位可以用3个连续等距时刻的水位，采用一个带动力修正项的水位预报模型进行预报，形式如下

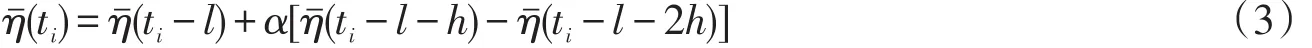
这里α[η¯(ti-l-h)-η¯(ti-l-2h)]称为动力修正项，α称为动力修正系数，l为预见期，h为3个连续时刻的时间间距。

假设天文潮水位可以用含如下若干个调和分潮和函数的形式表示

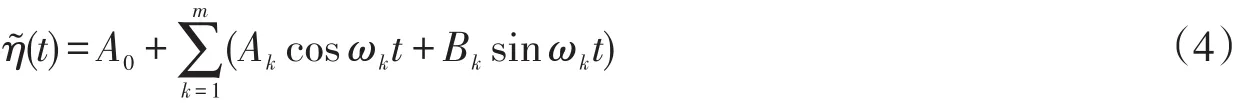
这里A0、Ak、Bk为调和分潮系数，m为分潮总数，ωk为第k个分潮的角速度。

分别利用式（3）和（4）对径流水位η¯(ti)和天文潮水位η~(t)进行预报，为求出动力修正系数和调和分潮系数的值，根据最小二乘法建立水位均方差目标函数如下

这里预见期l和时间间距h为整数。

据式（2）有

这里

据式（4）有

这里

故有

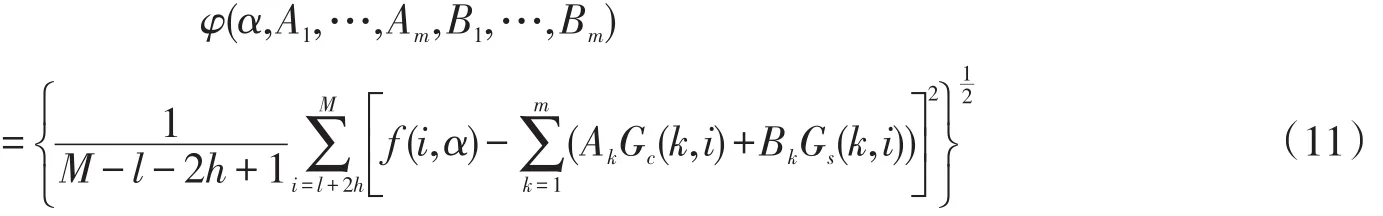
由于Gc(k,i)和Gs(k,i)为 α的函数，为使目标函数达到最小值，由 φ(α,A1,…,Am,B1,…,Bm)分别对α,A1,…,Am,B1,…,Bm的导数为零，形成了非线性的代数方程组。利用调和分析法和梯度下降法给出了辨识模型参数α,A1,…,Am,B1,…,Bm的迭代算法如下：

（1）给定辨识精度指标ε＞0，α的初始值α0。

（2）当 α=α0时，为得到 φ(α0,A1,…,Am,B1,…,Bm)的最小值，需满足 φ(α0,A1,…,Am,B1,…,Bm)对 Al、 Bl(l=1,2,…,m)的导数等于0。又因为=0，其中x表示A1,…,Am,B1,…,Bm，则有

经化简可得2m元一次方程组

解方程组（13）可以得到A1,…,Am,B1,…,Bm的值。

（3）给定学习速率初值λ=λ0，学习次数限定值Ktotal，学习次数计数器knum=1。

（4）将α作为未知量，对式（11）求导，可以得到

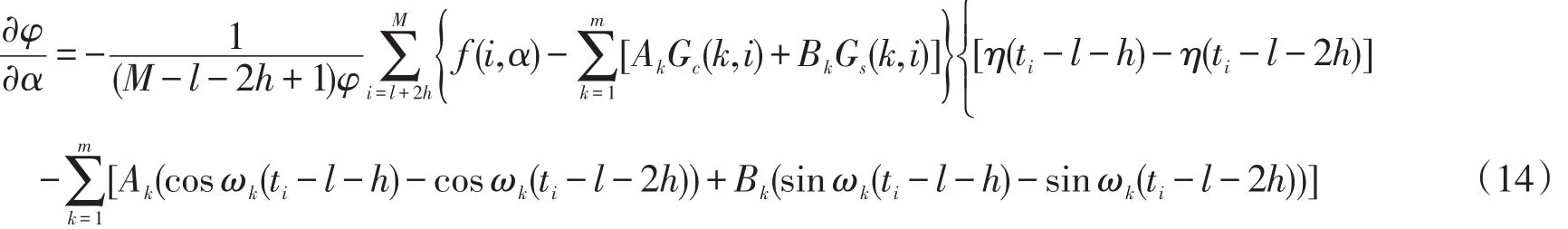
表1 基本调和常数Tab.1 Basic harmonic constant

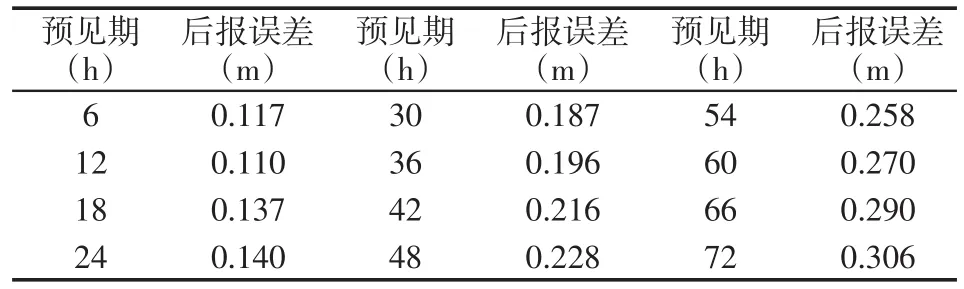
表2 南京2011～2012年水位预报模型后报误差Tab.2 Hindcast error of water level of Nanjing from 2011 to 2012

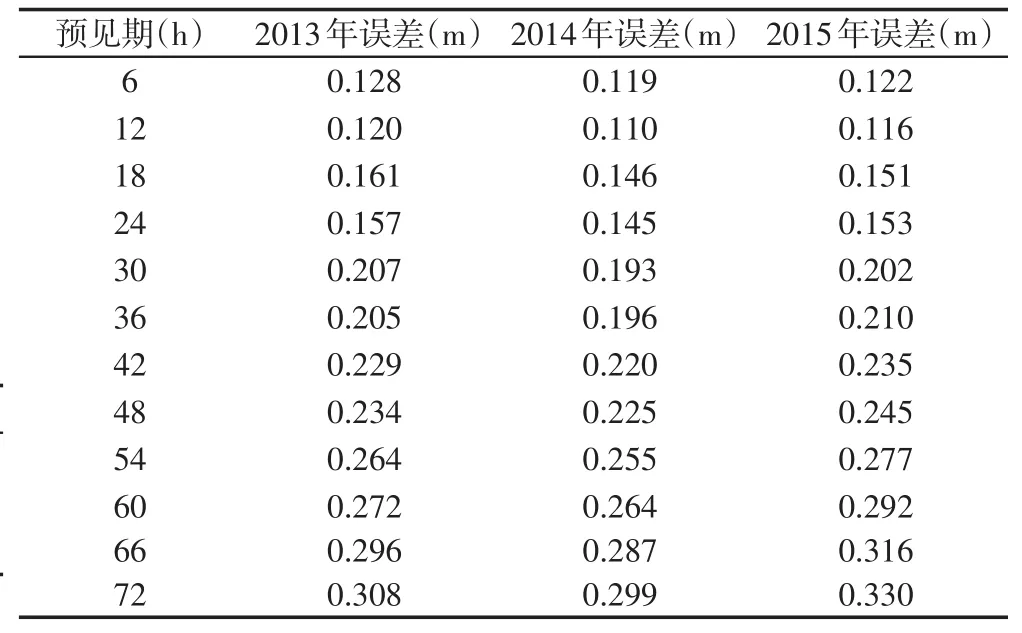
表3 南京2011～2012年水位后报参数预报2013～2015年水位误差Tab.3 Forecast error of the water level from 2013 to 2015 based on the hindcast parameters of the water level of Nanjing from 2011 to 2012

表4 南京2013～2015年预报误差分布（预见期6 h）Tab.4 Distribution of forecast error of Nanjing from 2013 to 2015（forecast period 6 h）

表5 南京2013～2015年预报误差分布（预见期24 h）Tab.5 Distribution of forecast error of Nanjing from 2013 to 2015（forecast period 24 h）

利用迭代得到的模型参数α,A1,…,Am,B1,…,Bm，可以完成当前站位的水位预报工作。对于任意时刻t，由式（2）和（3）得

这 里η(t)、η(t-h)和η(t-2h)为 已 知 数 据 ，将α,A1,…,Am,B1,…,Bm带入式（15），结合式（4），可以得到当前站位t+l时刻的预报水位η(t+l)。

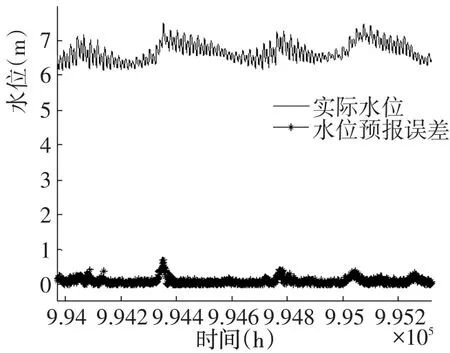
图1 南京2013年预报水位误差与实际水位对比分析（局部）Fig.1 Contrast between the error of forecast water level and the actual water level of Nanjing in 2013

2 水位预报模型的检验

在模型的计算检验过程中，选择潮汐的11个分潮进行调和分析计算，包括4个全日分潮、4个半日分潮和3个主要的浅水分潮，其分潮角速度见表1。

将感潮河段单站等时距水位优化预报模型应用于长江下游感潮河段。限于已有数据，利用南京2011～2012年全年等时距水位数据，对模型参数α和调和常数进行辨识，并作后报检验（表2）。再对2013～2015年的南京站水位进行预报，预报的均方差见表3。

后报及预报的预见期可根据需要进行调整，这里选择6～72 h间共12个时间长度作为预见期。由表2、表3数据可以看出，整体水位后报及预报精确度良好，尤其当预见期为12、24、36、48、60、72 h，误差较小。同时，针对预报的误差情况进行了分析，表4、表5主要反映了南京站预报水位在预见期为6 h和24 h的误差分布，可以看到当预见期为6 h、限定误差精度为0.3 m时，合格率在97%～98%。为保证合格率在85%以上，预见期可以选取36 h以内时长。而图1可以看到，水位预报误差整体较小，部分误差较大的预报时刻主要集中在径流变化趋势较大的时间段。

模型的验证可以看到，整体预报误差和传统的结合上下游数据的水位预报模型结果［14］相比不差，部分地方甚至较好，且该模型可以针对不同预见期进行预报。由此可见，该水位优化预报模型具有一定的可行性和实用性。

3 总结与展望

限于目前感潮河段的水位预报基本都需要上游径流水文观测站和下游海洋潮位观测站的数据，若出现上下游站位数据缺失等突发情况时，感潮河段单站等时距水位优化预报模型可以作为很好的替代模型使用，其独立性保证了模型不会受到上下游数据缺失的影响而进行较为准确的水位预报。同时，与现有模型相比，该水位预报模型更好地挖掘了现有的水文数据信息，数据利用率较高。且该模型整体预报精度较好，预见期可根据需要灵活调整，在保证精度的前提下，最长可以预报36 h的水位，适用性更强。因此，在只关注感潮河段水位变化的情况下，便不需要花费更多的人力和物力设立上下游的水文站。后期，可以将该模型改造成实时校准并连续预报的模式，加入洪水期和枯水期因素，增加其预报精度。还可以将模型与现有感潮河段水位模型进行结合，进一步改进现有水位预报方法，提高水文数据的利用率，改善预报结果。

［1］刘晓波，彭文启，刘静玲，等.基于POM模式的感潮河段三维水动力模拟［J］.水力发电学报，2009，28（1）：89-94. LIU X B，PENG W Q，LIU J L，et al.3⁃D numerical simulation of tidal flow based on POM model［J］.Journal of Hydroelectric Engi⁃neering，2009，28（1）：89-94.

［2］张小琴，包为民，马德莲.双向波水位演算模型参数动态修正［J］.河海大学学报：自然科学版，2010，21（5）：71-76. ZHANG X Q，BAO W M，MA D L.Dynamic correction of parameters for bi⁃directional stage routing model［J］.Journal of Hohai University：Natural Sciences，2010，21（5）：71-76.

［3］林勋励.长江口天文潮预报修正的一种方法［J］.海洋预报，1985（1）：34-42. LIN X L.An adjusting method of astronomical tide forecast in the Changjiang estuary［J］.Marine Forecast Service，1985（1）：34-42.

［4］Supharatid S.Tidal⁃level forecasting and filtering by neural network model［J］.Coastal Engineering Journal，2003，45（1）：119-137.

［5］Hidayat H，Hoitink A J F，Sassi M G，et al.Prediction of Discharge in a Tidal River Using Artificial Neural Networks［J］.JOUR⁃NAL OF HYDROLOGIC ENGINEERING，2014，19（8）：DOI：10.1061/（ASCE）HE.1943-5584.0000970.

［6］陈尚渭，金兆森.长江潮位预报方法的研究［J］.水利学报，1989，6：41-47. CHEN S W，JIN Z S.Study of Method of Predicting Tidal Level at Lower Reach of the Yangtze River［J］.Journal of Hydraulic Engi⁃neering，1989，6：41-47.

［7］黄国如，芮孝芳.感潮河段设计洪水位计算的频率组合法［J］.水电能源科学，2003，21（2）：72-74. HUANG G R，RUI X F.Design Flood Water Level for Tidal Reach with Frequency Combination Method［J］.Water Resources and Power，2003，21（2）：72-74.

［8］Smith P J，Beven K J，Horsburgh K.Data⁃based mechanistic modelling of tidally affected river reaches for flood warning purposes-An example on the River Dee，UK［J］.Quarterly Journal of the Royal Meteorological Society，2013，671（139）：340-349.

［9］Speer P E，Aubrey D G.A study of non⁃linear tidal propagation in shallow inlet/estuarine systems Part II：Theory［J］.Estuarine，Coastal and Shelf Science，1985，21（2）：207-224.

［10］Godin G.The propagation of tides up rivers with special considerations on the upper Saint Lawrence River［J］.Estuarine，Coastal and Shelf Science，1999，48（3）：307-324.

［11］Nidzieko N J.Tidal asymmetry in estuaries with mixed semidiurnal/diurnal tides［J］.Journal of Geophysical Research：Oceans（1978-2012），2010，115（C8）.

［12］Li G F，Xiang X Y，Wu J，et al.Long⁃Term Water⁃Level Forecasting and Real⁃Time Correction Models in the Tidal Reach of the Yangtze River［J］.JOURNAL OF HYDROLOGIC ENGINEERING，2013，18（11）：1 437-1 442.

［13］Moftakhari H R，Jay D A，Talke S A，et al.A novel approach to flow estimation in tidal rivers［J］.Water Rrsources Research，2013，49：4 817-4 832.

［14］方新.长江感潮河段水位过程预报模型研究［D］.南京：南京师范大学，2014.

Nonlinear optimal forecast model of water level at time knots with constant time interval from a single station of tidal reach

WANG Ru⁃yun1,LI Dan2,ZHOU Jun3,WANG Tian2
（1.College of Oceanography,Hohai University,Nanjing 210098,China;2.College of Harbor,Coastal and Offshore Engineering,Hohai University,Nanjing 210098,China;3.College of Hydrology and Water Resources,Hohai University,Nanjing 210098,China）

The current water level forecast models of tidal reach are subject to the observation data of water lev⁃el from the current tidal reach station,the runoff stations upstream and the tide stations downstream.It leads to the problems as follows:the leading time is subject to the time of the flow from the upstream;if the data at the upstream or the downstream are missed,the forecast would not be able to proceed;the acquisition of the data is high in cost. Assuming that the water level of tidal reach was linearly controlled by the runoff and tide,the paper built a nonlin⁃ear optimal forecast model with respect to one dynamic correction coefficient of runoff and a set of tidal harmonic co⁃efficients,which was based on the water level at time knots with constant time interval from a single station.Then, combining the curve fitting least square method,the harmonic analysis method and the gradient descent method,an iterative algorithm was proposed for solving the forecast model.The model was applied to some stations of the tidal reach of Yangtze River for test.Numerical experiences show the feasible and applicable of the model.

time knots with constant time interval;tidal reach;tidal harmonic analysis;nonlinear optimal fore⁃cast model

TV 133；P 731.23

A

1005-8443（2017）02-0132-05

2016-12-01；

2017-03-28

中国江苏省水利科技重点项目（2010500312）；中央高校基本科研业务费专项资金（2014B06314）

王如云（1963-），男，安徽芜湖人，教授，主要从事物理海洋学和港口海岸与近海工程研究。

Biography：WANG Ru⁃yun（1963-），male，professor.