后台阶下游水流泥沙运动模拟研究
孙建军,张庆河
(天津大学水利工程仿真与安全国家重点实验室,天津300072)
海岸河口及港口工程
后台阶下游水流泥沙运动模拟研究
孙建军,张庆河
(天津大学水利工程仿真与安全国家重点实验室,天津300072)
利用计算流体力学软件OpenFOAM和离散元软件LIGGGHTS建立的水流-泥沙运动耦合模型对后台阶下游三维水流流动及泥沙的起动和输运进行了数值模拟。结果表明,动态一方程紊流模型能较好模拟台阶下游时均流场、紊动强度以及雷诺应力的分布,通过耦合模型计算得到的台阶下游泥沙起动概率以及床面输沙率分布与实验结果符合较好。计算结果揭示在台阶下游复杂水流条件下,紊流结构及涡旋运动对泥沙起动有重要作用,而时均流动对床面输沙起关键作用。
LES⁃DEM耦合模型;后向台阶流;动态一方程紊流模型;泥沙运动
复杂流动下的泥沙起动和输运是河流、海岸工程研究的重点课题,一直受到人们的关注。目前,复杂流动下的泥沙输运问题通常依赖于经验公式,往往通过床面切应力公式或挟沙力公式得到输沙率[1-3]来进行计算。近年来,随着离散元法(DEM)的发展,运用计算流体力学(CFD)与离散元法(DEM)耦合数值模型,从细观尺度模拟水流泥沙运动得到了快速发展[4-6],能够刻画大量泥沙颗粒在近床面运动的细节,它有可能揭示复杂流动下泥沙颗粒的运动规律。苏东升等[7]基于计算流体力学开源软件OpenFOAM、离散颗粒开源软件LIGGGHTS以及CFDEM耦合库[8-9],建立了描述水流泥沙运动的离散颗粒模型,从细观尺度研究了明渠流中近床面泥沙的一般运动规律,但将其应用于复杂流动下泥沙运动规律研究的工作几乎没有,本文将在上述工作的基础上研究后台阶下游的三维水流与泥沙运动规律。
1 LES⁃DEM耦合模型
1.1流体控制方程及紊流模型
1.1.1 控制方程
OpenFOAM中,考虑颗粒组分影响的三维不可压流体运动的控制方程由以下连续性方程和动量方程组成
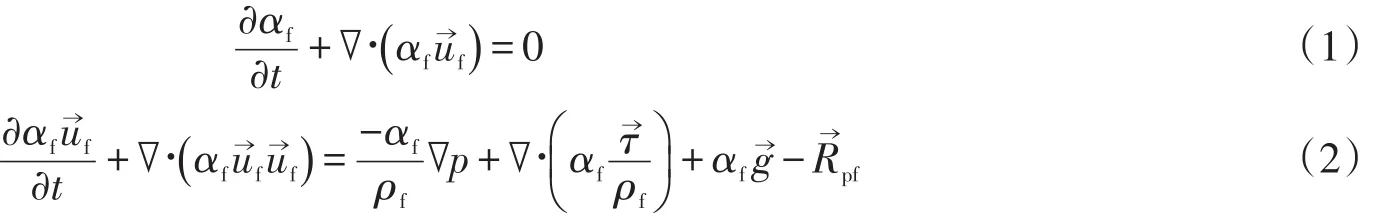
式中:αf为流体所占据的体积分数;f为流体的速度向量;p为流体压力;为重力加速度向量;为流体有效应力的张量;pf为颗粒与流体之间交换的动量项。
1.1.2 紊流模型
为了使整个控制方程封闭,运用大涡模拟(LES)方法,LES方程向N⁃S动量方程中引入了额外的应力,称为亚格子尺度应力(简称SGS应力),为求解SGS应力,其中以涡粘假设为基础的理论公式如下

Samgorinsky模型是目前广泛应用的亚格子模型,但由于其采用单一常数Cs计算νsgs,会存在耗散过大问题[10]。因此本文采用动态一方程模型,即计算系数随空间和时间调整的动态模型

式中:ksgs代表亚格子紊动动能,采用以下控制方程求解

1.2 颗粒运动控制方程
LIGGGHTS颗粒模型中,离散颗粒的运动遵循牛顿第二定律,其控制方程包含平动和转动两部分[11]

为准确合理地描述颗粒运动,确定颗粒之间和颗粒与固壁间受力以及颗粒所受的流体作用力是模型的关键。苏东升[7]的研究结果表明,颗粒之间和颗粒与固壁间的接触碰撞采用Hertz⁃Mindlin无滑移软球模型[12],流体作用于颗粒上的拖曳力采用Benyahia拖曳力公式[13]可以较好描述上述相互作用力。

图1 计算域(单位:m)Fig.1 Computational domain
1.3颗粒与流体运动的耦合
LES⁃DEM耦合模型,流体运动采用OpenFOAM中基于PISO算法的瞬态不可压缩流体求解器求解,颗粒运动采用LIGGGHTS计算,利用基于Open⁃FOAM程序框架的CFDEM耦合库完成流体和颗粒之间的相互作用力计算及信息传递。其计算过程分以下步骤[14]
(1)LIGGGHTS程序计算颗粒运动;
(2)CFDEM耦合库计算颗粒所在网格单元的体积分数;
(3)CFDEM耦合库计算流体与颗粒之间相互作用力,从而得到动量交换项;
(4)耦合库计算得到的相互作用力传递至LIGGGHTS程序;

图2 台阶下游平均流速剖面(Z=2.5D处)Fig.2 Mean streamwise velocity profiles at the downstream of the stepZ=2.5D
(5)基于动量交换项,OpenFOAM程序求解流体运动,并传递至CFDEM耦合库;
(6)重复步骤1~5。

图3 台阶下游时均流速矢量场图(Z=2.5D处)Fig.3 Mean streamwise velocity vectors at the downstream of the stepZ=2.5D
2 后台阶流场模拟
为保证模型流场计算结果的合理性,首先对台阶下游床面无泥沙颗粒的情况进行数值模拟并和实验结果进行比较以验证模型的合理性。计算域范围为-5D≤X≤20D,0≤Y≤5D 0≤Z≤5D,D为台阶高度,计算域如图1所示。
入流边界水流流速根据对数流速剖面原理给定[15]
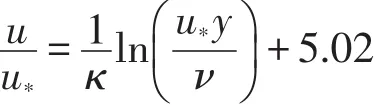
式中:u为不同水深处的流速;u*为摩阻流速;ν表示运动粘滞系数;κ表示卡门常数,取0.41,保证模拟的入流平均流速U0=0.2 m/s,流动雷诺数ReD=U0D/ν=5 000,上边界采用滑移边界条件,底边界采用无滑移边界条件,Z轴方向设为循环边界。上述计算条件与Jovic和Driver实验条件一致[16]。
根据Le等[17]模拟研究,本文模拟时间取ttotal=400D/U0=50 s,流场时均统计时间取ΔTave=109D/U0≈14 s,可以获得合理时均流场与紊动特征。
2.1 时均流速剖面验证
根据大涡模拟的瞬时流场进行时均统计,得到台阶下游平均流速剖面。图2给出了本文计算得到的平均流速剖面与Jovic和Driver实验[16]的对比结果,可以看出,数值模拟结果与实验结果一致。图3为台阶下游时均流速矢量场图,由图可知,在台阶后流动会出现分离,形成回流区,超过这一位置,分离流重新附着床面(再附),逐渐恢复为对数剖面,可以看出X=4D位置处在回流区内,X=6D位置在再附点附近。
2.2 紊动强度与雷诺应力验证
图4~图6显示了后台阶下游紊动强度与雷诺应力的计算结果与实验结果,图7为台阶下游紊动强度分量与雷诺应力的三维剖面图。由图可知,在0.5D高度台阶位置,流向和垂向紊动强度都较强,在床面附近,流向紊动强度较大,而垂向紊动强度则较小。
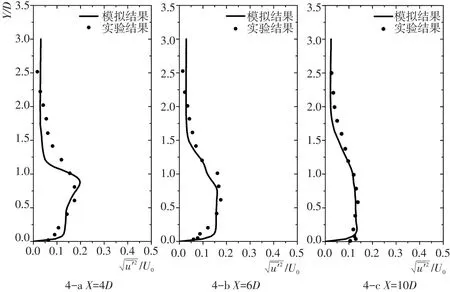
图4 台阶下游流向紊动强度剖面Fig.4 Relative streamwise turbulence intensity profiles at the downstream of the step
3 台阶下游泥沙输运模拟
3.1 模拟参数设定
刘春嵘[18]采用图像技术研究了后台阶下游床面泥沙的起动概率,并建立数学模型进行了数值模拟,为方便对比验证模型,本文采用与刘春嵘实验相同的模型布置,在台阶下游20D长度范围内随机铺设100 000个泥沙颗粒,颗粒直径d=0.425 mm,密度 ρs=1 400 kg/m3,计算流体密度ρf=1 000 kg/m3,动 力 粘 滞 系 数μ=10-6kg/m·s,颗粒计算的Hertz⁃Mindlin无滑移“软球”模型参数如表1所示,流体与颗粒计算的时间间隔分别为Δtf=10-3s和Δtp=10-5s,颗粒每计算100步与流体进行一次耦合。
本文根据泥沙运动速度的大小来判断泥沙是否起动,在某时刻t,沿台阶下游以0.4D宽为间隔分区域统计不同位置处的泥沙起动概率Pit,起动的颗粒数目与该区域颗粒总数之比即为该区域t时刻的泥沙起动概率Pit,统计时间间隔为0.05 s,共取200个时刻值进行平均,从而得到该位置处的泥沙起动概率Pi。
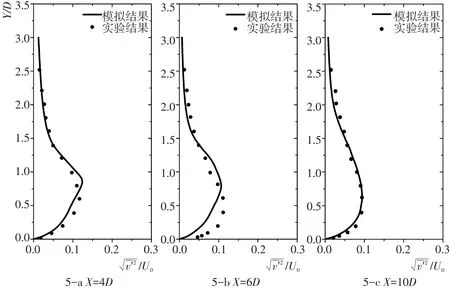
图5 台阶下游垂向紊动强度剖面Fig.5 Relative vertical turbulence intensity profiles at the downstream of the step

图6 台阶下游雷诺应力剖面Fig.6 Relative Reynolds stress profiles at the downstream of the step
图8 给出了本文计算得到的台阶下游不同位置处泥沙的起动概率Pi,并与刘春嵘的实验结果及数值模拟结果进行了比较,可以看出,本文计算结果与实验值基本一致,在靠近台阶区域泥沙起动概率较低,随着距台阶距离的增大,泥沙起动概率逐渐增大,在再附点振荡区域内达到最大值。
3.2 泥沙输运
目前关于床面泥沙输运问题的研究,大部分是基于平直槽道流动下的结果,一般都以床面切应力作为泥沙起动输运的水动力因素[19],而在复杂流动条件下,由于涡旋以及强紊动作用的存在,只考虑平均床面切应力因素并不合适,Nelson等[20]利用LDV测速技术对后台阶下游泥沙输运与紊动相互作用问题进行了研究,Dou等[21]将涡量强度、紊动强度等因素等权重线性叠加,建立了输沙率模型,这些工作都是对复杂流动下泥沙运动水动力机制的初步探索,这里采用大涡模拟准确模拟流场,并与离散颗粒模型耦合,从细观尺度上研究复杂流动条件下泥沙的运动规律。

图7 台阶下游紊动强度及雷诺应力分布图Fig.7 Turbulence intensity and Reynolds stress profiles at the downstream of the step
本文根据Nelson等人[20]的实验布置进行算例设计,台阶高度D=0.04 m,泥沙颗粒粒径服从高斯分布,中值粒径d50=0.9 mm,标准差为σ=0.1 mm,密度ρs=2 650 kg/m3,泥沙颗粒随机均匀平铺在台阶下游床面,共计415 000个颗粒。
初始计算时,固定泥沙颗粒直至流场紊流充分发展稳定后,释放床面泥沙颗粒开始运动,并持续模拟30 s。为保证结果的准确性,结果统计分析取后20 s时间内的数据。沿着台阶下游顺流方向,以0.01 m宽为间隔分区域计算不同位置处的瞬时输沙率qsx,再进行长时间的统计平均得到不同位置处的平均输沙率q¯sx。根据泥沙颗粒的瞬时速度可以计算得到泥沙的瞬时输沙率,公式如下


表1 模型中颗粒参数Tab.1 Particle parameters used for the present simulation
无量纲输沙率公式如下
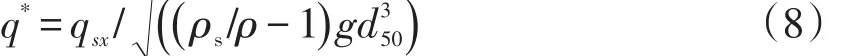

图8 台阶下游不同位置处的泥沙起动概率比较Fig.8 Comparison of the sediment incipient probability at the downstream of the step
式中:up,i为第i个泥沙颗粒的速度;Vp,i为第i个泥沙颗粒的体积;A为模拟区域平面的面积;ρs为颗粒密度。
图9~图10给出了台阶下游床面附近(Y=0.005 m)不同位置处的平均流速及流向紊动强度,图11为台阶下游纵向时均流速矢量场图,图12给出了后台阶下游的平均无量纲输沙率q¯*,并与Nelson的实验结果以及Schmeeckle模拟结果[22]进行了比较,可以看出,在回流区内,平均输沙率为负,床面泥沙向上游输运,在平均再附点(X/D≈6)附近,虽然由于大尺度涡的存在导致紊动强度较大,泥沙起动概率较大,但附近平均流速接近为零,故造成床面平均输沙率较低。

图9 台阶下游不同位置处的平均流速(Y=0.005 m)Fig.9 Mean streamwise velocity at the downstream of the stepY=0.005 m
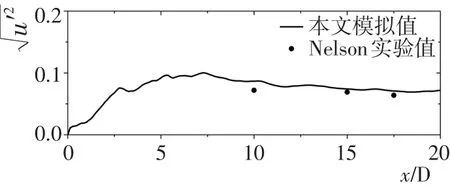
图10 台阶下游不同位置处的流向紊动强度(Y=0.005 m)Fig.10 Streamwise turbulence intensity at the downstream of the stepY=0.005 m

图11 台阶下游时均流速矢量场图(Z=0.05 m处)Fig.11 Mean streamwise velocity vectors at the downstream of the stepZ=0.05 m

图12 台阶下游不同位置处的平均无量纲输沙率比较Fig.12 Comparisons of mean dimensionless sediment transport rates at the downstream of the step
4 结论
本文利用计算流体力学软件OpenFOAM和离散元软件LIGGGHTS建立的水流-泥沙运动耦合模型,从细观尺度研究了后台阶下游三维紊流流动以及床面泥沙的起动和输运内部机制,主要得到以下结论:
(1)动态一方程紊流模型能较为准确地模拟后台阶下游复杂的三维紊流流动,计算得到的时均流速、紊动强度及雷诺应力剖面与实验结果符合较好,保证了模型水动力条件的合理性。
(2)分析得到0.5D高度台阶处,流向和垂向紊动强度都较强,在床面附近,流向紊动强度较大,而垂向紊动强度较小。
(3)模拟得到的台阶下游平均输沙率与实验结果较为一致,回流区内平均输沙率为负,床面泥沙向上游输运,平均再附点附近,虽然大尺度涡的存在导致紊动强度较大,泥沙起动概率较大,但由于附近平均流速接近为零,造成平均输沙率较低。
(4)在后台阶下游复杂流动条件下,涡旋及紊动作用对泥沙起动起主要作用,而对泥沙输运起重要作用的是时均流动。
[1]Niemann S L,Fredsøe J,Jacobsen N G.Sand dunes in steady flow at low Froude numbers:Dune height evolution and flow resis⁃tance[J].Journal of Hydraulic Engineering,2010,137(1):5-14.
[2]Chou Y J,Fringer O B.A model for the simulation of coupled flow⁃bed form evolution in turbulent flows[J].Journal of Geophysical Research:Oceans,2010,115(C10).
[3]Nguyen Q,Wells J C.A numerical model to study bedform development in hydraulically smooth turbulent flows[J].Journal of Hy⁃draulic Engineering,2009,53(1):157-162.
[4]王光谦,孙其诚.颗粒物质及其多尺度结构统计规律[J].工程力学,2009,26(S2):1-7. WANG G Q,SUN Q C.Granular matter and the scaling laws[J].Engineering Mechanics,2009,26(S2):1-7.
[5]Zhu H P,Zhou Z Y,Yang R Y,et al.Discrete particle simulation of particulate systems:a review of major applications and findings[J].Chemical Engineering Science,2008,63(23):5 728-5 770.
[6]肖锋军,郭烈锦,王跃社,等.三维混合沙输运数值模拟[J].工程热物理学报,2012,33(2):259-262. XIAO F J,GUO L J,WANG Y S,et al.A 3⁃dimensional simulation of mixed sand transport[J].Journal of Engineering Thermophys⁃ics,2012,33(2):259-262.
[7]苏东升,张庆河,孙建军,等.基于CFD-DEM耦合方法的近床面水流泥沙运动模拟研究[J].水道港口,2016,37(3):224-230. SU D S,ZHANG Q H,SUN J J,et al.Simulation of fluid⁃sediment particle motion near bed based on CFD⁃DEM coupling method[J].Journal of Waterway and Harbor,2016,37(3):224-230.
[8]Sadaghiani M R S,Jentsch H,Faulstich K,et al.DEM modeling and identification of representative element volume of soil skeleton[J].Numerical Methods in Geotechnical Engineering,2014:403.
[9]Zhao J,Shan T.Coupled CFD⁃DEM simulation of fluid⁃particle interaction in geomechanics[J].Powder technology,2013,239:248-258.
[10]张海涛,曹曙阳.基于动态亚格子模型的方柱绕流大涡模拟[J].沈阳建筑大学学报:自然科学版,2013,29(3):434-439. ZHANG H,CAO S Y.Large Eddy Simulation of Flow Past a Square Cylinder Based on Dynamic Sub⁃Grid Scale Models[J].Jour⁃nal of Shenyang Jianzhu University,2013,29(3):434-439.
[11]胡国明.颗粒系统的离散元素法分析仿真[M].武汉:武汉理工大学出版社,2010.
[12]孙其诚,光谦.颗粒物质力学导论[M].北京:科学出版社,2009.
[13]Benyahia S,Syamlal M,O'Brien T J.Extension of Hill⁃Koch⁃Ladd drag correlation over all ranges of Reynolds number and solids volume fraction[J].Powder Technology,2006,162(2):166-174.
[14]Goniva C,Kloss C,Hager A,et al.An open source CFD⁃DEM perspective[J].Proc Openfoam Workshop,2010.
[15]刘春晶,李丹勋,王兴奎.明渠均匀流的摩阻流速及流速分布[J].水利学报,2005,36(8):0950-0955. LIU C J,LI D X,WANG X K.Experimental study on friction velocity and velocity profile of open channel flow[J].Journal of Hy⁃draulic Engineering,2005,36(8):0950-0955.
[16]Jovic S,Driver D M.Backward⁃facing step measurements at low Reynolds number,Reh=5000[J].NASA Tech Mem,1994:94.
[17]Le H,Moin P,Kim J.Direct numerical simulation of turbulent flow over a backward⁃facing step[J].Journal of Fluid Mechanics,1997,330(1):349-374.
[18]刘春嵘.复杂流动下底床局部冲刷实验和数值模拟研究[D].北京:中国科学院力学研究所,2003.
[19]Rijn L C V.Sediment Pick⁃Up Functions[J].Journal of Hydraulic Engineering,1984,110(10):1 494-1 502.
[20]Nelson J M,Shreve R L,McLean S R,et al.Role of near⁃bed turbulence structure in bed load transport and bed form mechanics[J].Water Resources Research,1995,31(8):2 071-2 086.
[21]Dou X B.Using A 3⁃D Model to predict local scour[C]//Steven R.Water Resource Engineering 98.Memphis,Tennessee,ASCE,1998:198-203.
[22]Schmeeckle M W.The role of velocity,pressure,and bed stress fluctuations in bed load transport over bed forms:numerical simu⁃lation downstream of a backward⁃facing step[J].Earth Surface Dynamics,2015,3(1):105.
Simulation of fluid⁃sediment particle motion at the downstream of backward⁃facing step flow
SUN Jian⁃jun,ZHANG Qing⁃he
(State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China)
Using computational fluid dynamics software OpenFOAM and particle motion simulation software LIGGGHTS,a coupled fluid⁃particle model was presented and applied in the investigation of three⁃dimensional tur⁃bulence,sediment incipience and sediment transport at the downstream of the backward⁃facing step flow.The simu⁃lation results show that the dynOneEqEddy LES model can describe the mean velocity profile,the turbulence inten⁃sity and the distribution of Reynold stress well.The probability of sediment incipience and the sediment flux ob⁃tained by the coupled model at the downstream of the backward⁃facing step agree well with the experiment.The re⁃sults indicate that the turbulence and large⁃scale vortices induce the sediment incipience and the mean flow contrib⁃utes to its transport in the case of complex flows at the downstream of the backward⁃facing step.
LES⁃DEM coupled model;backward⁃facing step flow;dynOneEqEddy LES model;sediment mo⁃tion
TV 142;O 242.1
A
1005-8443(2017)02-0109-06
2016-11-03;
2017-01-13
国家自然科学基金资助(51179122)
孙建军(1990-),男,山东省潍坊人,硕士研究生,主要从事港口海岸及近海工程研究。
Biography:SUN Jian⁃jun(1990-),male,master student.

