钢铁企业蒸汽系统多周期优化策略

陈骏，周伟国，王海

（同济大学机械与能源工程学院，上海 200092）

钢铁企业蒸汽系统多周期优化策略

陈骏，周伟国，王海

（同济大学机械与能源工程学院，上海 200092）

钢铁企业蒸汽系统具有汽源设备较多、能源品种多以及能源供需及价格变化等特点，本文以某大型钢铁企业实际运行的蒸汽动力系统为研究对象，综合考虑其各台锅炉设备的不同生产特点、企业的能源需求和能源价格随时间变化的规律以及设备启停运行转换产生一部分费用等因素建立约束条件，以全时段蒸汽系统总能源成本最低为目标函数，建立蒸汽-电力耦合的多周期、混合整数非线性规划模型（MINLP），利用基于数学规划方法的LINGO软件求出全局最优解。通过分析比较，证明初始运行条件对多周期优化结果有很大影响，影响效果会延续数个周期，同时LINGO计算求解全局最优解的效率高、结果合理、可行，并能够为企业在能源设备调度上提供依据，实现一个运行时段内的低成本和高效益。

蒸汽系统；多周期；数学模型；混合整数非线性优化；优化

钢铁制造业在我国是主要的高能耗行业之一，其占我国能源总消耗的15%左右，在我国钢铁生产的单位能耗相比发达国家要高出约20%，未来还有巨大的节能潜力[1]。蒸汽系统是钢铁企业生产过程中必不可少的能源系统，据统计大型钢铁企业蒸汽系统能耗占总能耗的10%左右[2]，有进一步节能的空间。通过合理的动力优化[3]协调系统始、末段的产能、耗能关系可以提高蒸汽系统整体运行效率，对企业能源系统节能降耗、降低总体生产成本具有重要意义。

钢铁企业蒸汽系统的一个典型特点就是设备的多工况变化，其主要原因之一是负荷需求的多周期变化，另外也有能源价格的多周期变化这一因素引起生产方式的改变。目前已有大量对蒸汽系统多时段、多周期优化进行研究的文献报告[4-17]，文献[9]对5个时间段的煤气-蒸汽-电力耦合模型以费用最低进行了最优化求解，文献[10-14]考虑了锅炉和汽轮机的效率随工况变化下的总成本最优，文献[15]计算了考虑设备的维修周期的最优运行，文献[16-17]则将环境成本纳入模型，文献[18]考虑了能源价格的周期变化。本文以某大型钢铁企业为背景，根据其蒸汽系统运行的实际情况，采用数学规划方法建立多汽源设备、多能源品种及多时间段蒸汽-电力耦合的混合整数非线性规划模型（MINLP）。考虑各设备实际产能、各周期内的能源供需和能源价格等条件作为约束，以蒸汽系统全周期总成本最低为目标，利用LINGO11软件求得全局最优解。其结果为全时段内满足能源需求前提下的总能源成本最低运行方案，可以为生产调度提供依据。

1 问题的提出

钢铁企业蒸汽系统存在以下几个特点。首先，蒸汽系统中存在诸多能源品种及转换形式，有动力煤、富余煤气[14]的形式，也有电力、蒸汽这样的二次能源形式。第二，钢铁企业一方面在产能端存在不同类型的设备，这些设备在运行方式上也有所不同，如燃煤锅炉、干熄焦余热炉和燃气锅炉等，且锅炉热效率随着运行负荷变化而改变；另一方面在需求侧，用户对能源的需求也各异，如低压蒸汽、中压蒸汽。因此需要对蒸汽系统进行合理的生产调配来保证供需平衡，使整个系统经济和高效的运行。第三，蒸汽系统随时间变化的特点：其一，供需随时间的变化导致设备有不同的运行方式，不同时段的需求会导致不同的运行策略，如调节抽汽式汽轮机既可以在凝汽工况也可在抽汽工况运行分别满足用电需求或供热需求；其二，有些能源价格随时间变动较大，如动力煤价格冬季明显高于其他时期，因此能源价格会影响不同时段的设备运行策略，即外购电价高时采购动力煤发电或者当煤炭价格高时放弃外购煤炭直接购买电力满足需求，最优的运行方式需要根据目标函数和约束条件经优化计算来确定；其三，锅炉启动运行前需要一系列包括仪器标定、水压及阀门测试等准备工作，启动过程一般耗时5h以上并耗费大量燃料，停运过程也同样会产生费用，因此不同时段之间设备启停运行策略的转换会产生运行调整费用，同时由于各时段的能源需求和能源单价不同导致下一时段的运行策略不同。

另外，多时段、多周期问题往往存在计算上的困难。一般对于单一时段进行优化的模型来说模型的规模（决策变量的个数）主要取决于设备数量，而在多时段、多周期模型中，随着时间段的增加决策变量的个数成倍增加，同时相邻两个时段又会产生设备启停变化的问题，由于设备启停变化产生的费用计入目标函数，启停变量将不同时段内的决策变量关联到了一起，形成了大型耦合矩阵，随着时段的增加计算机的求解耗时将呈指数增加，导致计算困难[4,19]。

2 优化策略

根据该企业的实际情况，充分考虑了以下几个关键点，并以此为依据建立蒸汽管网的数学模型。

第一，不同的燃料供应不同设备，以及将设备产能（蒸发量）和能源分配（供热或供电）作为约束条件，另外企业正常生产情况下设备的生产负荷变化在一定的区间内，因此尝试简化锅炉运行效率随负荷变化的关系来减少模型的非线性程度，从而减少计算量。

第二，本文以半个月15个生产日为1个时段，即1个月有2个时段，并对4个月共8个时段进行计算，且认为1个时段内设备只能有1种运行方式，不同时间段的运行方式（启停、负荷）可以不同，但是不同时段设备运行方式改变会产生相应的启停费用，不同设备有其相应的启停费用。另外，由于考虑设备启停费用，不同的初始运行方式会影响下一时间段内的能源费用，所以为了适应实际生产调度的需要，模型还设定了初始工况，可以根据当前实际的运行方式来计算将来整个时间段内的成本最低运行方式。

第三，考虑了各时段不同的能源需求，能源供给必须满足需求，同时各时段的能源单价不一，由于从企业得到的能源平均单价数据是以月来统计，从而一个月中的2个时段能源单价相同，由于每个月的能源单价不同，因此能源需求和单价会共同对该时段的运行策略产生影响。

第四，将每个时间段的能源使用量乘以对应能源的单价再与全时段内设备启停运行方式改变所产生的费用相加，对全时段能源总费用求最小值，该值即为目标函数，所得到的结果即是全时段跨度内能源总成本最低的运行方式。

目前针对多周期模型的优化计算方法主要分为两大类：人工智能算法和数学模型规划法。人工智能算法包括遗传算法、粒子群算法等进化算法，其中遗传算法的使用极为普遍，文献[19-20]是采用遗传算法的代表。遗传算法虽然适用性好，但是其使用过程中需要大量参数设置，如选择、交叉、变异算子、精英群体个数、收敛准则等，另外计算时长和过早收敛问题也导致使用不便[21-24]。因此，本文试图对多周期问题进行合理简化，并采用基于数学模型规划法的全局最优求解器LINGO，其能够快速准确地完整覆盖整个搜索域，求解成功率也极高。文献[25]给出了对约1000个样本采用LINGO计算全局最优解的测试报告，结果表明当自变量不超过99个（包含整数变量）时，其在900s内完成求解并得出正确结果的样本数超过95%，显示其较强的求解能力和较高的准确率。

3 蒸汽系统模型建立

该企业蒸汽系统按压力等级分为中压（4MPa，260℃）、低压（1.6MPa，260℃）两个蒸汽系统。共有6个汽源设备，其中低压锅炉（LBoiler）和135t/h锅炉（T135）是以高炉煤气、焦炉煤气和转炉煤气为燃料的燃气锅炉机组，低压锅炉只提供低压蒸汽，而T135锅炉机组带有1台背压式汽轮机发电机组，可向中压蒸汽管网供汽或者通过减温减压设备输出低压蒸汽，也可以将中压蒸汽供应汽轮机发电，背压输出低压蒸汽再进入低压蒸汽管网。系统中共有3台干熄焦余热锅炉机组（CDQ），燃料为余热，2#CDQ为抽汽凝汽式机组，其可通过调节抽汽凝汽比例来调节供汽量和发电量。3#CDQ和4#CDQ分别为背压式和纯凝式汽轮机发电机组。

3.1 设备模型及运行工况

首先从企业得到的数据可知该企业的富余煤气和余热资源供给比较稳定，可视为恒定，其次为了简化模型对月平均价格波动小于年平均价格10%的能源按照年平均价格作为固定值计算，其余能源的价格按照各时间段内的价格分别计算。第三，锅炉运行效率简化的可行性分析，图1为该企业135t/h燃气锅炉（T135）的效率与蒸发量关系，图中曲线是通过最小二乘法拟合得到的非线性方程，由于该设备在主要负荷段（锅炉负荷LT135为40～100t/h）内效率与蒸发量的关系变化不大，因此考虑按恒定效率计算，同理低压锅炉（LBoiler）其效率（图2）按常数0.91处理，其他锅炉设备也作类似处理。将锅炉效率视作常数主要目的是为了缩小模型规模和降低计算机求解难度，以及减少求解过程中的时间消耗。

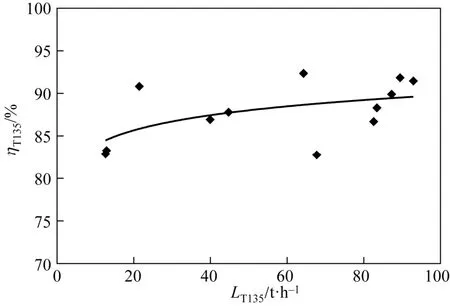
图1 T135锅炉效率曲线

图2 低压锅炉（LBoiler）锅炉效率曲线

3.2 设备启停逻辑约束

考虑到锅炉设备在实际生产中必须稳定运行避免反复启停运作，同时又应当避免大产能设备小产量产出（大马拉小车）的不经济工况，故采用整数模型的逻辑约束，即当决策变量为判断某设备是否运行时只能有0（停运）和1（运行）两种结果，并且当设备运行时，其蒸发量产能不低于最大产汽能力的30%，该约束适用于各时段，见式(1)。

式中，Wkj表示第k个时段内第j台设备是否运行；Pkj表示第k个时段内第j台设备的产汽发生量。

3.3 设备启停操作模型

全时段各产能设备的启停操作模型为：当前时段某产能设备为运行而下一时段为停运，则计为1次操作，反之亦然，两个时段期内设备启停不变时启停操作次数为0，某设备全时段内启停操作总费用为总操作次数乘以单次操作费用，不同设备的启停操作费用不同，见式(2)。

式中，Twkj表示第k个时段内设备j相对于上个时段是否有启停变化；CTw，j表示j设备一次启停操作的费用，共有m台产能设备、p各时段。

3.4 目标函数

目标函数为全时段内蒸汽系统的总能源成本最低，其包括整个系统内设备投入所消耗的能源（包括设备运行消耗的电、动力煤和自用汽）及原料（纯水和工业水）乘以相应能源的单价费用，加上外购电力单价费用，设备进行一次启停操作所产生的费用（富余煤气和余热为企业生产过程中所产生的能源不计入总费用），可表示为式(3)。

式中，Eki,j为第k个时段内第j台设备上第i种能源的使用量，共n个能源品种，由于能源需求负荷的单位是小时量，因此不同时段计算得到的费用也是小时费用，需乘以各时段的小时数后求和得到全时段总费用。

3.5 设备运行负荷约束

锅炉设备在运行时的发生量会受到产能的限制，经过不同工艺的减温减压设备可以同时生产中压和低压蒸汽，两者又同时受到减温减压设备的产能约束，适用与各时段，模型约束可表示为式(4)～式(6)。

3.6 富余煤气消耗约束

富余煤气是高炉煤气、焦炉煤气和转炉煤气的总和，其首先满足燃气锅炉的生产需求，剩余的煤气送入电厂与动力煤共同作为电厂燃料，其值与燃气锅炉的效率和负荷有关，适用于各时段，见式(7)。

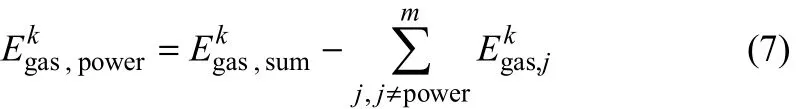
3.7 调节抽汽式汽轮机抽汽约束

对于抽汽凝汽式汽轮机，如果汽轮机运行且开启抽汽供热时，则抽汽量大于汽轮机空载耗气量，见式(8)。

式中，Gkj为第k个时段内设备j的抽气量；Gj,0为设备j的空载耗气量。

3.8 蒸汽、电力需求约束

能源需求与能源产出需保持平衡，即每个时间段内各产汽设备的总产汽量等于各用能单位的总需求量，各时段发电设备的总发电量加上外购电量等于总需求量，见式(9)～式(11)。

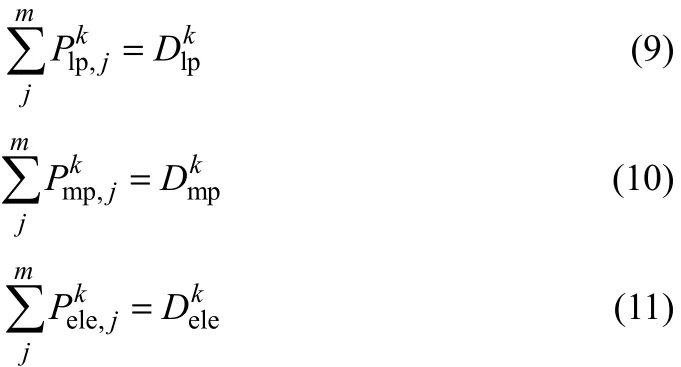
4 实例计算与结果分析

4.1 实例计算

该钢铁企业各汽源设备的最大产能如表1。为了减少计算量，对该企业4个月（9～12月份）、8个运行时段进行优化，并以半个月（15天）为1个时段，1个时段内设备处于相同的运行工况，同时富余煤气总量不变且不计入能源总成本、余热资源费用也不计入目标函数。各时段、周期内的能源需求量及能源价格见表2、表3。对于月平均价格波动小于年平均价格10%的能源按照年平均价格计算，并列于表3。初始设备启停状态见表4，0表示设备停运，1表示设备运行。不同设备的启停操作费用列于表5。模型有6个产能设备，表示设备启停的二进制变量6个，每个时段设备产出不同种类的能源用21个决策变量表示（包括外购能源），一个时段总计27个决策变量，总的模型规模为8个时段（9～12月份）共计216个决策变量（设备初始运行状态为已知）。需要特别说明的是企业在实际生产过程中的设备运行工况是6台设备全部投入运行。最后对全部8个时段以蒸汽系统的能源总成本最低为目标函数，采用LINGO11全局最优解器进行计算，优化结果列于表6～表10。

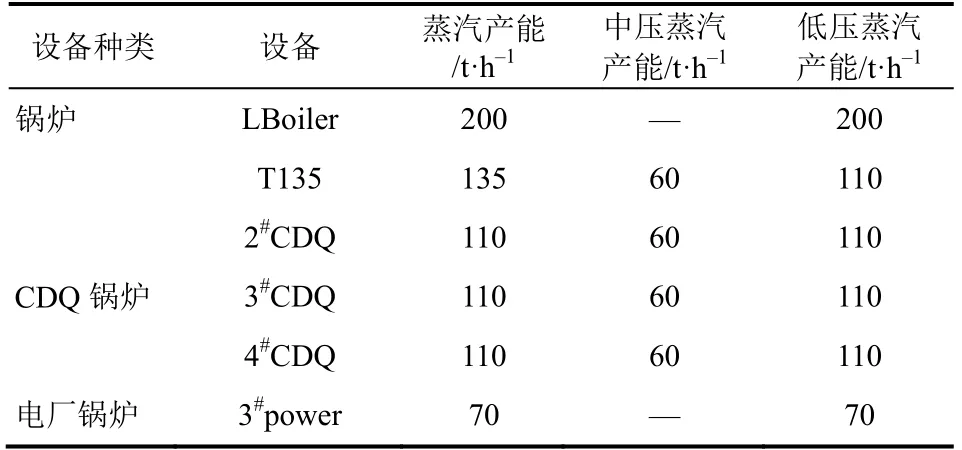
表1 各设备的产汽、供汽能力

表2 各时段能源需求总量

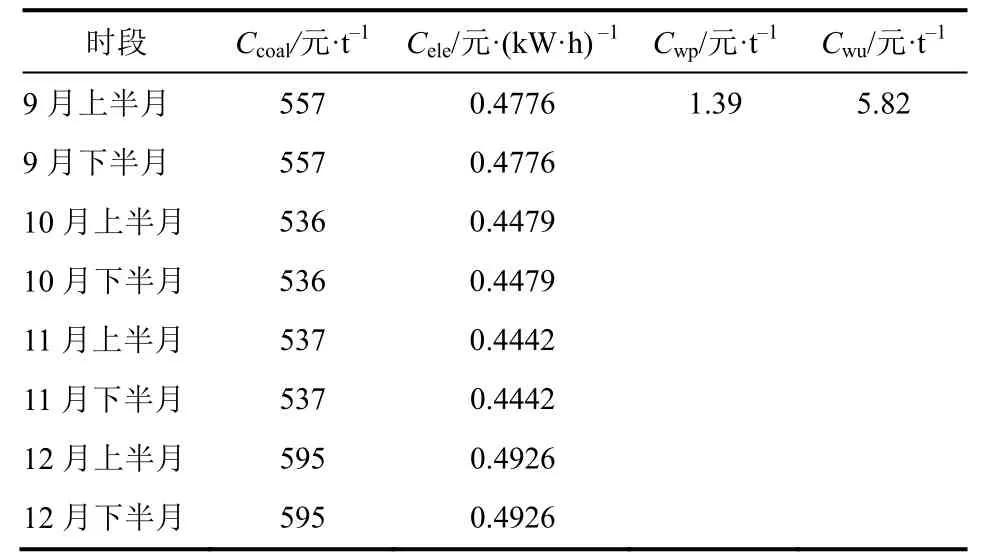
表3 各时段能源费用

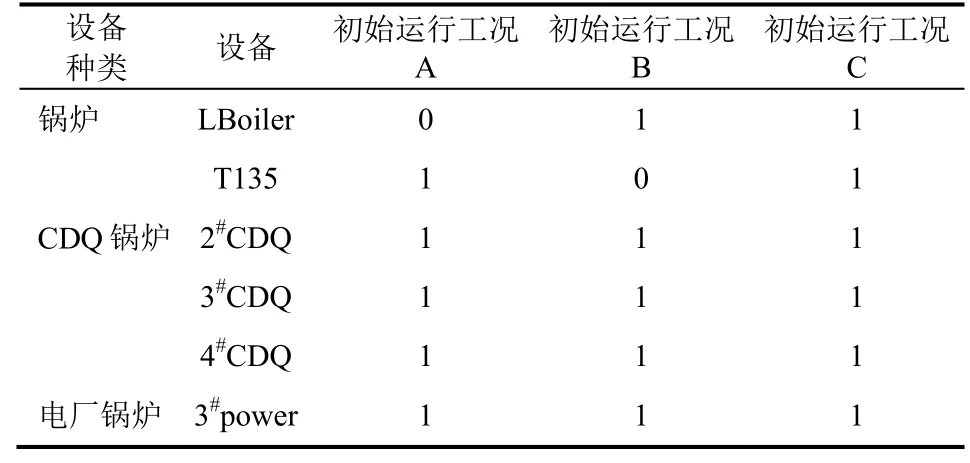
表4 初始运行状态

表5 设备启停转换操作费用

4.2 优化结果分析

首先，企业实际生产过程中在8个时段内6台设备是全部投入运行的，虽然可以满足能源需求更大幅度的变化，但从表6～表8中优化结果可以看出在满足月均能源负荷需求（蒸汽和电力）时只需要投入5台设备即可，而且低压锅炉的低压蒸汽产能仍有一定余量（表10中LBoiler列）可以挖掘，另外以低成本为目标的情况下也更倾向于投用低压锅炉。第二，以不同初始运行工况为初始条件从而得到的表6～表8中优化结果可以看出由于初始运行工况A和B的不同对全时间段内的设备的运行方式产生了巨大影响，甚至可以说全时段内以总能源成本最低为目标的各设备生产方式是由初始运行条件决定的，其根本原因是目标函数中纳入了设备启停操作费用和变动的能源单价，而且可以看出初始条件对优化的影响延续了4个时段。第三，将优化结果（表6、表7）与各时段能源需求总量（表2）相比较可以看出当能源需求量变化不大时，设备启停操作变化及其所产生的费用对设备运行方式产生了一定影响，具体表现为设备运行与上一时段一致，而当能源需求量变化较大时设备运行调整才显得有必要，表现为设备启停发生了变化。第四，表9列出了实际运行下的能源费用和根据3种初始工况优化后的各项费用，从中可以看出优化后能源费用有明显减少，即使由于设备启停产生了费用。第五，为了节省篇幅仅将工况C的运行结果列于表10，期中的数据显示全局最优的求解结果满足约束条件的情况较好；另外可以看出电厂锅炉外购动力煤自发电对降低全时段能源总成本是有利的，因此优化结果中没有采取外购电力的方式。第六，LINGO对该模型优化计算仅耗费10s、迭代小于5000步，求解效率较高。

表6 初始运行工况A下的各时段设备启停优化结果

表7 初始运行工况B下的各时段设备启停优化结果

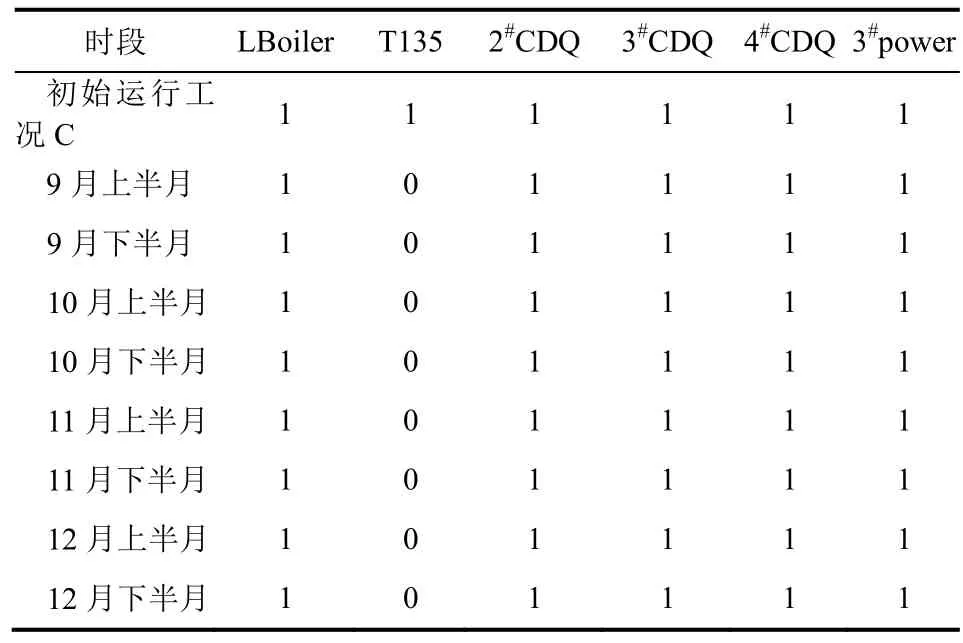
表8 初始运行工况C下的各时段设备启停优化结果

表9 优化结果比较

表10 根据初始运行工况C求得的各设备产能调配优化结果

5 结论

（1）通过合理简化设备运行参数使得基于数学规划法的LINGO软件能够处理复杂、模型规模较大的多周期优化问题，并能以较高的效率求得全局最优解。

（2）多周期、多时段问题由于涉及了设备启停操作费用和变动的能源单价，其最优解是与初始运行条件密切相关的，而且初始条件对计算的影响可以延续至数个时段。

（3）由于本模型考虑了设备运行的初始条件，因此可以根据企业当前设备所处于的运行状态规划未来一段时期的运行策略，即使遇到突发的设备运行变化事件，也可以重新计算来制定未来一段时期内的设备运行规划。

符号说明

C——某能源品种单价，元

Cost——全时段能源总成本，104元

D——某品种能源需求量

E——系统消耗能源的数量

L —— 锅炉负荷，t/h

min —— 最小值

P —— 产出某种能源

W —— 设备运行或停止运行

η —— 效率，%

下角标

boiler —— 锅炉设备

CDQ —— 干熄焦锅炉

coal —— 动力煤

ele —— 电力

gas —— 富余煤气

i —— 第i种投入能源

j —— 第j台设备

lp —— 低压蒸汽

mp —— 中压蒸汽

power —— 电厂锅炉

sum —— 合计

Tw —— 设备启停转换

wp —— 纯水

wu —— 工业水

上角标

k —— 第k个周期段

[1] GUO Z C，FU Z X. Current situation of energy consumption and measures taken for energy saving in the iron and steel industry in China[J]. Energy，2009，35：4356-4360.

[2] 张立宏，蔡九菊，杜涛，等. 钢铁企业蒸汽系统的现状分析及改进措施[J]. 中国冶金，2007，17（1）：50-53. ZHANG L H，CAI J J，DU T，et al. Present status analysis of steel enterprise steam system and its improvement measures[J]. China Metallurgy，2007，17（1）：50-53.

[3] 李德芳，索寒生，刘暄. 石化企业能源管理系统的研发与应用[J].化工学报，2015，66（1）：7-13. LI D F，SUO H S，LIU X.Development and application of energy management system for petrochemical enterprises[J]. CIESC Journal，2015，66（1）：7-13.

[4] IYER R R，GROSSMANN I E. Optimal multi-period operational planning for utility systems[J]. Computers Chem. Engng.，1997，21（8）：787-800.

[5] IYER R R，GROSSMANN I E. Synthesis and operational planning of utility systems for multi-period operation[J].Computers Chem. Engng.，1998，22（7）：979-993

[6] 鄢烈祥，胡晟华，麻德贤. 锅炉蒸汽系统多操作周期的优化调度[J]. 化工学报，2003，54（12）：1708-1712. YAN L X，HU S H，MA D X. Optimal multi-period operational planning for boiler steam systems[J].CIESC Journal，2003，54（12）：1708-1712.

[7] 戴文智，尹洪超，池晓. 改进PSO算法在蒸汽动力系统多周期运行优化中的应用[J]. 化工学报，2009，60（1）：112-117. DAI W Z，YIN H C，CHI X. Optimal multi-period operational planning of steam power systems using improved particle swarm optimization method[J]. CIESC Journal，2009，60（1）：112-117.

[8] 罗向龙，张高博，王智，等. 大型石化企业蒸汽动力系统运营优化[J]. 石油炼制与化工，2009，40（5）：48-52. LUO X H，ZHANG G B，WANG Z，et al. Operational management optimization of steam power system in large petrochemical enterprise[J]. Petroleum Processing and Petrochemicals，2009，40（5）：48-52.

[9] 张琦，提威，杜涛，等. 钢铁企业富余煤气-蒸汽-电力耦合模型及其应用. 化工学报，2011，62（3）：753-758. ZHANG Q，TI W，DU T，et al. Coupling model of gas-steam-electricity and its application in steel works[J]. CIESC Journal，2011，62（3）：753-758.

[10] 张国喜，华贲，刘金平. 石化企业蒸汽动力系统的多工况操作优化[J]. 石油炼制与化工，2009，32（5）：42-46. ZHANG G X，HUA B，LIU J P. Multi-period operational optimization for steam power system of petrochemical industry[J]. Petroleum Processing and Petrochemicals，2009，32（5）：42-46.

[11] 罗向龙，华贲，张冰剑. 炼油厂蒸汽动力系统优化调度策略研究[J].计算机与应用化学，2006，23（1）：41-45. LUO X L，HUA B，ZHANG B J. Optimal multi-period operational planning for steam power system of petrochemical industry[J]. Computers and Applied Chemistry，2006，23（1）：41-45.

[12] 张沛存，池晓，尹洪超，等. 石化企业蒸汽动力系统优化运行研究[J]. 热科学与技术，2009，8（4）：350-354. ZHANG P C，CHI X，YIN H C，et al. Optimal operational planning for steam power system in chemical process industry[J]. Journal of Thermal Science and Technology，2009，8（4）：350-354.

[13] 尹洪超，池晓，赵亮. 蒸汽动力系统多周期优化运行研究[J]. 节能，2008（7）：38-40. YIN H C，CHI X，ZHAO L. Optimal multi-period operational planning for steam power system [J]. Energy Conservation，2008（7）：38-40.

[14] 宋心东，尹洪超，翟勇，等. 多周期蒸汽动力系统运行优化研究[J].节能，2005（5）：10-13. SONG X D，YIN H C，ZHAI Y，et al. A study of optimal operation about multi-period steam power systems[J]. Energy Conservation，2005（5）：10-13.

[15] 张冰剑，华贲，刘金平，等. 石化企业蒸汽动力系统的多周期优化运行[J]. 华北电力大学学报，2005，32（2）：90-92. ZHANG B J，HUA B，LIU J P，et al. Optimal multi-period operations for steam power systems of chemical refinery complexes[J]. Journal of North China Electric Power University，2005，32（2）：90-92.

[16] 戴文智，尹洪超. 引入环境成本的石油化工企业蒸汽动力系统多周期运行优化[J]. 石油学报，2010，26（3）：448-455. DAI W Z，YIN H C. Optimal multi-period operational planning for steam power system of petrochemical industry with consideration of environment costs[J]. Acta Petrolei Sinica，2010，26（3）：448-455.

[17] 戴文智，于静梅，杨新乐. 低碳背景下蒸汽动力系统多周期运行优化[J]. 石油学报，2012，28（6）：955-1000. DAI W Z，YU J M，YANG X L. Optimal multi-period operational planning for steam power system under low-carbon economy[J]. Acta Petrolei Sinica，2012，28（6）：995-1000.

[18] 罗向龙，华贲. 炼油厂蒸汽动力系统优化调度策略研究[J]. 计算机与应用化学，2006，23（11）：1057-1060. LUO X L，HUA B. Study on steam power system operational optimization strategy[J]. Computers and Applied Chemistry，2006，23（11）：1057-1060.

[19] HARIHARAN G，DRAGOLJUB K. Operational planning of combined heat and power plants through genetic algorithms for mixed 0-1 nonlinear programming[J]. Computers & Operations Research，2015，56：51-67.

[20] MASATOSI S, KOSUKE K, SATOSHI U. Operational planning of district heating and cooling plants through genetic algorithms for mixed 0-1 linear programming[J]. European Journal of Operational Research，2002，137：677-687.

[21] MIRRZAZVI S K， JONES D F，TAMIZ M. A comparison of genetic and conventional methods for the solution of integer goal programmes[J]. European Journal of Operational Research，2001， 132：594-602.

[22] JONES D F, MIRRZAZVI S K, TAMIZ M. Multi-objective meta-heuristics：an overview of the current state-of-the-art[J]. European Journal of Operational Research, 2002，137：1-9.

[23] BANSAL R C. Optimization methods for electric power systems：an overview[J]. International Journal of Emerging Electric Power Systems，2005，2（1）：1-23.

[24] 陈骏，周伟国，王海，等. 基于等效电法的钢铁企业蒸汽系统多目标运行优化策略[J]. 化工学报，2016，67（9）：3804-3811. CHEN J，ZHOU W G，WANG H，et al. Multi-objective optimal strategy for steam power system in steel industry based on electricity equivalent calculation[J]. CIESC Journal，2016，67（9）：3804-3811.

[25] NEUMAIER A, SHCHERBINA O, HUYER W，et al. A comparison of complete global optimization solvers[J]. Math. Program, 2005，103：335-356.

Study on optimal multi-period operational strategy for steam power system in steel industry

CHEN Jun，ZHOU Weiguo，WANG Hai
（School of Mechanical Engineering，Tongji University，Shanghai 200092，China）

Steam power steam including a variety of energy producers and demand over time, is an essential part of iron and steel companies. Factors of different equipment units, various sums of energy demand in each period, energy prices fluctuations with period and expense of changeover of each equipment unit between periods were taken into consideration respectively in this paper. A mixed integer nonlinear programming（MINLP）model was established, which is multi-period and steam-electricity coupled. The objective function is the sum of cost of energy in steam and power system during whole periods. The global optimal solution will be achieved by LINGO software, The core of which is mathematical programming. Based on the result and analysis of the calculation, it is demonstrated that initial operation condition has great influence on the result of multi-period optimization and LINGO solves this kind of model with high efficiency and reliability. It is analyzed that optimization result is to achieve the lower cost and high economic operation, which could be the basis of production and operation by the administrator.

steam power system；multi-period；mathematical modeling；mixed integer nonlinear programming；optimization

TQ021.8

：A

：1000–6613（2017）05–1589–08

10.16085/j.issn.1000-6613.2017.05.005

2016-09-22；修改稿日期：2016-12-13。

陈骏（1985—），男，硕士研究生。联系人：周伟国，教授，博士生导师。E-mail：tjweiguo@tongji.edu.cn。