基于螺纹综合扫描仪的螺纹参数测量方法研究

（中国航空制造技术研究院，北京100024）

航空紧固件用于飞机装配过程中各零部件的连接，承载时在零部件直径传递载荷、协调变形。航空紧固件使用多种标准紧固件，包括螺丝、铆钉、螺栓和销等，还有一些新型的连接技术。这些连接方式的关键目标在于“质量安全”，而螺纹连接仍是飞机装配的主要连接方法。由于紧固件的大批量、互换性、大尺寸范围等特点，采用螺纹量规检验紧固件效率高但易磨损，因此必须定期校准螺纹量规。螺纹的高质量和高性能不仅取决于先进的加工工艺，还依赖于精确的测量方法。

螺纹量规包括螺纹塞规和螺纹环规，其基本参数有：大径、中径、小径、螺距和牙型半角[1]，而中径、螺距和牙型半角是影响螺纹互换性的主要参数。传统的螺纹量规测量方法分为接触式和非接触式两类。接触式测量包括采用测长机、螺纹综合测量仪和三坐标测量机等仪器测量的方法。非接触式测量主要指影像法，即在万能工具显微镜上测量。

本文通过比较几种螺纹量规测量方法的特点，分析采用螺纹综合扫描仪测量螺纹全参数的误差源，并估计该测量方法的测量不确定度。以螺纹综合指标为判定依据，能更有效地保证螺纹的质量安全。准确测量螺纹量规的综合参数，并实现量值传递，为航空紧固件产品的质量控制提供了有力依据。

1 传统螺纹量规测量方法比较

1.1 测长机测量螺纹

利用三针法在测长机（图1）测量外螺纹单一中径，首先通过被测螺纹的螺距及牙型半角选择最合适三针直径，然后装夹三针并移动使其与螺纹中径接触，调节仪器，最后软件自动计算螺纹中径。利用T型红宝石测头在测长机上测量内螺纹单一中径，与外螺纹测量原理相同，调节工作台在水平前后移动及绕水平轴旋转两个方向的调整，保证测头在轴截面上与量规直径接触，自动计算中径[2]。

利用测长机测量螺纹量规的单一中径，是一种单参数测量方法，其效率较高，但是由于单一中径是通过螺距和牙型角计算出的，因此对于螺距和牙型角加工控制不严的产品，其单一中径存在较大不确定度。

图1 测长机示意图Fig.1 Measuring machine

1.2 万能工具显微镜测量螺纹

利用万能工具显微镜测量螺纹的基本参数（包括螺距、大径、中径、小径和牙型角），是一种光学测量方法，如图2所示。首先将显微镜立柱倾斜一个螺纹升角，调节其焦距，使牙廓在轴平面上清晰；然后通过移动工作台和显微镜镜头测量螺纹的各个参数。

利用万能工具显微镜，单次测量可测出多个螺纹参数，操作简单、经济性好且测量精度高。但测量人员的人为因素会带来测量误差且效率较低，影像法无法测量螺纹环规，对螺纹量规的螺纹表面质量要求高，以便于显微镜对焦。

图2 万能工具显微镜示意图Fig.2 Universal tool-measuring microscope

1.3 三坐标测量机测量螺纹

利用三坐标测量机测量螺纹参数时，通过探针与螺纹牙侧面的接触，直接记录各点的坐标值并进行拟合，即可确定探针的测量路径和测量位置，如图3所示。根据拟合的牙侧面坐标，计算出其余参数[3]。

图3 三坐标测量机测量螺纹示意图Fig.3 CMM measuring the thread

三坐标测量机测量法自动化程度高，无需找到最佳直径的测针，测量精度高且效率高。但由于三坐标测量机的探针尺寸偏大，限制了对小尺寸螺纹以及内螺纹的测量，而且仪器成本高。

综上所述，这3种传统的螺纹测量方法均有不足之处，如效率低下、参数不齐全、零件尺寸受限制等，且对一些内螺纹，仅以单一中径判定合格标准，存在技术风险。如实完整地再现螺纹的实际情况，以螺纹综合状态作为判定依据，才能使螺纹质量得到保证。除此之外，螺纹多参数的准确测量是螺纹溯源的基础。目前基于螺纹综合扫描仪的螺纹多参数测量方法是研究的一个热点，其测量精度可靠、自动化程度高、测量范围大、效率高[4-7]，单次装夹可完成一个量规的全参数测量，包括大径、中径、小径、螺距、牙型半角、螺距累计误差和螺旋升角等，且测量结果几乎不受人工操作影响。

2 基于螺纹综合扫描仪的螺纹测量原理

本文研究内容选用的测量仪器是荷兰IAC公司生产的MSXP螺纹综合扫描仪，利用该仪器测量螺纹参数是一种高精度的接触式测量方法，其测量范围在1～100mm内，2min可完成螺纹全部参数的测量。测量原理如图4所示。

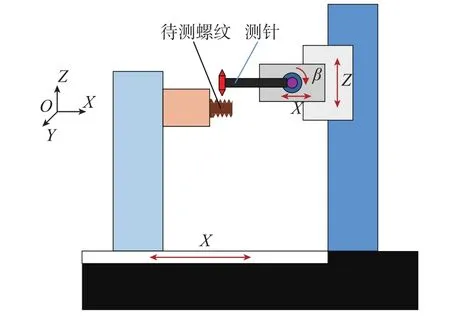
图4 螺纹综合扫描仪测量原理Fig.4 Measurement principle of the thread integrated scanner

在参考坐标系O-XYZ下，待测螺纹及量规被夹持固定在可在X方向上直线运动的滑块上，手动控制；测针可在X和Z方向上发生宏位移，在绕Y轴转动的β轴上做微转动。其中，X向运动平台由直线电机驱动，Z向运动平台由直线电机和精密气浮系统驱动。由图5可见，探针在被测螺纹的某一轴向剖面上获取其轮廓曲线，探针运动轨迹的位置坐标由位置传感器反馈得到，在Z轴方向控制其接触力恒定不变。在接触到被测螺纹表面后，机械探针在该轮廓上进行连续的扫描运动，随后在与其轴线对称的轮廓上连续扫描以获得螺纹的轮廓曲线，经计算转换为螺纹的各参数信息，包括大径、中径、小径、螺距和牙型角等[8]。

由于螺纹综合扫描仪在记录螺纹表面的扫描曲线时，存储的是测针在接触螺纹时的坐标点数据，即测针在参考坐标系下的姿态，而螺纹实际的形貌曲线应是测针在螺纹坐标系下采集的数据坐标。因此，建立螺纹坐标系与测针坐标系之间的误差模型是非常有必要的。

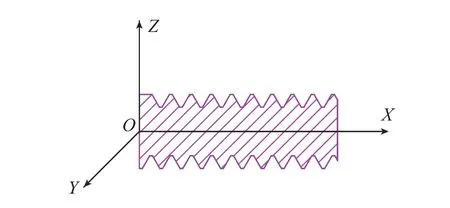
图5 被测螺纹轴向剖面轮廓Fig.5 Axial profile of the measuring thread

3 螺纹综合扫描仪误差分析与建模

3.1 测量系统误差参数分析

螺纹综合扫描仪在测量过程中，存在一定的测量误差，这些误差由静态误差和动态误差综合引入。其中，静态误差主要包括仪器由于加工精度引起的几何误差和装配误差，以及由于温度变化导致的热误差；动态误差主要包括各轴的几何运动误差、测量系统的动态响应性能、由气浮轴承的稳定性导致的误差等。本文主要分析高精度运动平台的几何误差引入的测量误差，首先找出几何误差源，然后建立该测量系统的误差传递模型[9]。

为了方便建立多自由度系统的误差综合模型，将测量系统的各运动轴假设为刚体，引入齐次坐标变换方法。齐次坐标变换矩阵是机器人运动学中用来描述两个刚体的空间位姿关的4×4的矩阵，它提供了用矩阵运算把二维、三维甚至多维空间中的一个点集从一个坐标系变换到另一个坐标系的有效方法。

多体系统是指由多个物体通过运动副连接的系统，是对相互连接的刚性或柔性体的动力学行为的研究。一般用拓扑结构描述一个多体系统中各物体的联系方式[10]。螺纹综合扫描仪测量系统显然是一种多体系统，本文采用多体系统理论建立该测量系统的误差传递模型。本文描述的综合测量仪机构示意图如图6所示。根据多体理论，对系统各部件定义单元体坐标系：在系统基台上建立参考坐标系0；螺纹上建立坐标系1；X向运动轴上建立坐标系2；Z向运动轴上建立坐标系3；Y向转动轴上建立坐标系4；测针上建立坐标系5。

图6 综合测量仪机构示意图Fig.6 Sketch map of the integrated scanner

在三维空间中，刚体有6个自由度，即3个平移自由度和3个旋转自由度，本文用6个方向误差描述一个导轨的运动误差。将螺纹和测针的装夹误差也分为6个方向上的分量。考虑到螺纹综合扫描仪的测量原理，螺纹参数由扫描曲线处理计算获得，而扫描曲线上的点坐标由位置传感器记录，又由于测针在扫描螺纹表面轮廓时是接触式测量，因此测针和螺纹在X、Z方向的定位精度和Y方向的转动精度并不影响扫描点的坐标位置与精度。该测量系统的几何误差源如表1所示。其中，δ表示直线位移误差量，θ表示角度位移误差量，φ表示轴间垂直度误差量，其下标数字表示运动的单元体，下标括号内的字母表示误差方向。

3.2 综合误差建模过程

根据多体系统理论，假设坐标系oi-xiyizi由坐标系先作转动，再作平动得到oj-xjyjzj，则oj-xjyjzj到oi-xiyizi的变换矩阵为：

式中，Tijs称为体间理想运动特征矩阵，x、y、z、α、β、γ分别为坐标系oi-xiyizi相对于坐标系oj-xjyjzj在X、Y、Z 3个自由度方向上的直线位移和角度位移，c为cos的简写，s为sin的简写。又各角度位移均很小，故取其正弦值取0，余弦值取1。下面将详细描述测量系统几何误差的建模过程。

（1）螺纹相对于基座的齐次坐标变换包括两个部分：螺纹坐标系原点相对于参考坐标系原点的偏移变换和装夹误差坐标变换矩阵。变换矩阵为：

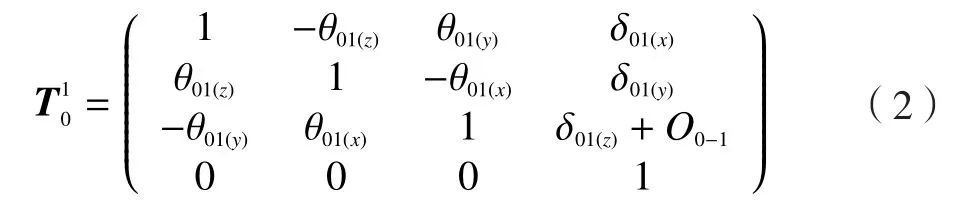
表1 测量系统的几何误差源

式中，O0-1为螺纹坐标原点和基座坐标原点在z方向上的偏移量；δ01（x），δ01（y），δ01（z）分别为线性位移误差和直线度误差；θ01（x），θ01（y），θ01（z）分别为螺纹在 x 方向的滚转、y方向的俯仰和z方向的偏摆误差。下面的变换矩阵元素定义与此类似，不再逐一叙述。

（2）X向运动轴相对于基座坐标系齐次坐标变换包括两个部分：X轴坐标系原点相对于参考坐标系原点的偏移变换和运动误差坐标变换矩阵。变换矩阵为：

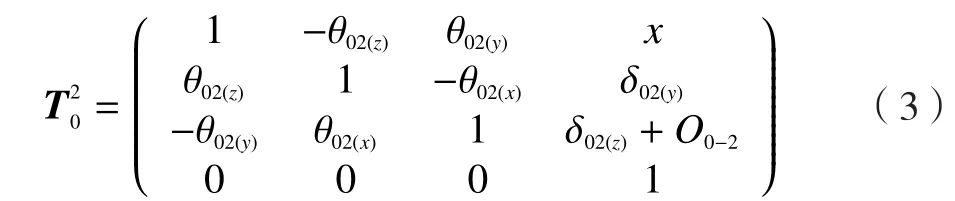
式中，x表示X运动轴的位移。

（3）与X轴相比，Z轴的坐标系增加了1个由于两个运动轴之间垂直度φ23误差引起的变换矩阵。因此Z轴相对于X轴的误差变换矩阵为：

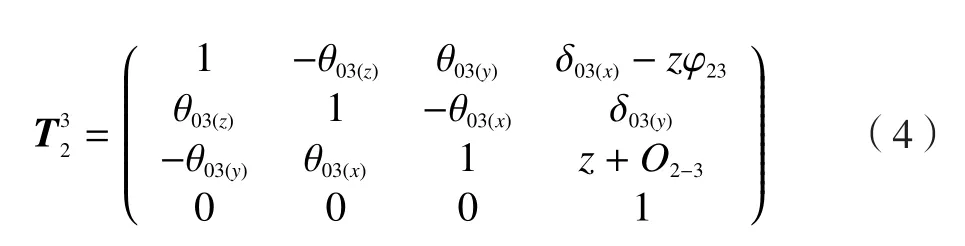
式中，z表示Z运动轴的位移。

（4）类似地，Y向转动轴相对于Z轴的误差变换矩阵包括3部分：坐标原点平移变换矩阵；由垂直度误差φ24、φ34引入的变换矩阵和运动误差坐标变换矩阵。

（5）测针相对于Y轴的齐次坐标变换只包括其装夹误差坐标变换矩阵。变换矩阵为：

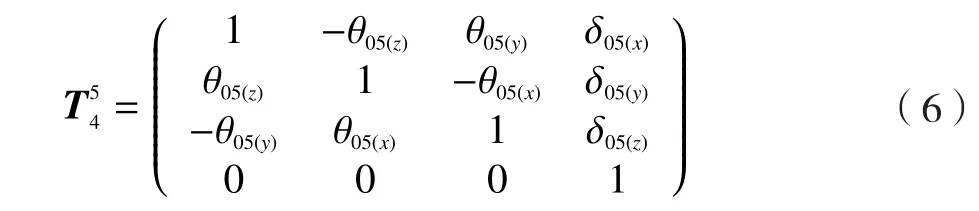
在理想状况下，测针和螺纹相对于参考坐标系的变换矩阵分别为：

式中，为没有运动误差时向量之间对应的变换矩阵。从测针到螺纹坐标系的齐次坐标变换矩阵为：

测针在螺纹坐标系下的位置向量为：

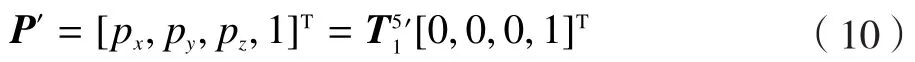
测针在螺纹坐标系下的方向向量为：

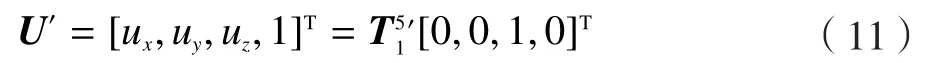
实际上，各坐标系之间的齐次变换矩阵均包括误差的传递，则从测针坐标系到螺纹坐标系的误差传递矩阵为：

测针在螺纹坐标系下的位置向量为：

测针在螺纹坐标系下的方向向量为：

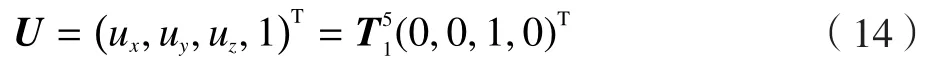
则，测针在螺纹坐标系下的位置误差向量和方向误差向量分别为：

3.3 误差结果分析

螺纹综合扫描仪的运动轴均采用精密气浮驱动并配有高精度光栅尺反馈，因此其运动精度非常高。统一取线误差分布范围（0，0.001mm），角误差分布范围（0，0.001°），代入误差传递矩阵，计算得测针在螺纹坐标系下的位置误差向量最大为 [1.08，1.74，0.05，0]，方向误差向量最大为 [0.004，0.006，0.0003，0]。螺纹扫描仪通过测针在螺纹上的接触点坐标位置计算其参数，因此由测量系统几何误差引入的接触点位置误差最大为（1.08，1.74，0.05）mm。

由计算结果可以看出，测针的接触点坐标在参考坐标系和螺纹坐标系下的误差在X和Y方向非常大，在Z方向上比较大。但是，由于测量系统的运动误差分布规律遵循正态分布，因此每个运动单元的单项误差在最大值的概率很小，经多自由度精密运动轴的误差传递，在螺纹坐标系引入的最大偏差在最大值的概率几乎为0。

螺纹综合测量仪的测量精度与其主机性能、传感器分辨率、标准器制造精度、测针的选取以及光栅尺精度等相关。当然，最主要的因素是光栅尺精度和传感器分辨率，该仪器光栅尺分辨率高达0.01μm，传感器分辨率为0.01μm。由于光栅尺的反馈作用，传感器识别到的测针位置是经过误差自动补偿的，而上述部分计算出的最大位置误差在其补偿控制范围内。因此，测针描绘出的轨迹逼近螺纹表面形貌的真值。

3.4 测量结果对比

分别利用测长机、万能工具显微镜、三坐标测量机和螺纹综合扫描仪对M12和M20的通端螺纹塞规测量其中径，测量值如表2所示。经过螺纹中径实测值的对比发现，利用螺纹综合扫描仪测量螺纹的中径值与测长机等的测量误差在2μ m以内，测量准确。

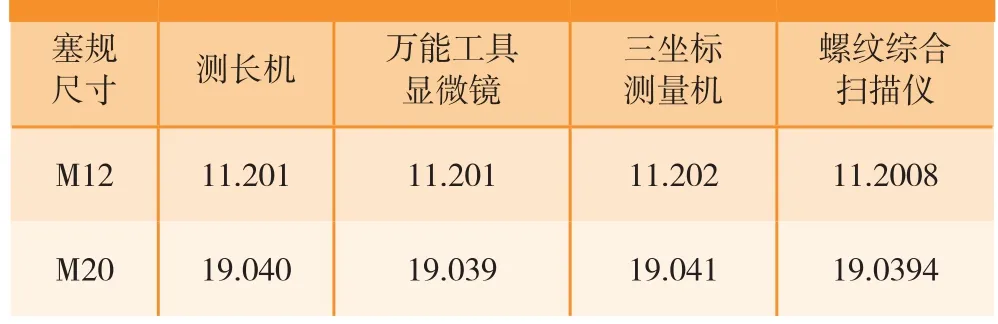
表2 螺纹中径测量结果比对 mm

利用螺纹综合扫描仪对M24的通端螺纹塞规进行稳定性测量，每两个月测量一次，共5次，其中中径、螺距、大径和牙型半角的测量结果如表3所示。试验表明，该螺纹综合扫描仪稳定性良好。

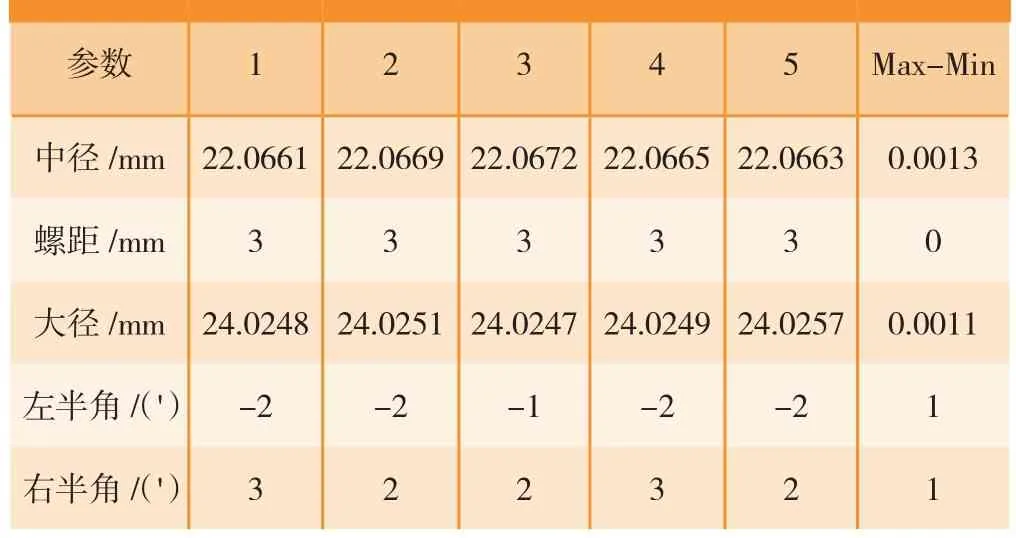
表3 螺纹综合扫描仪稳定性试验结果

再对该仪器做重复性试验，计算其标准偏差，同样满足测量要求，在此不做赘述。

4 结论

利用螺纹综合扫描仪测量螺纹表面轮廓是一种高精度的接触式全参数测量方法。本文通过分析测量系统的几何误差参数，建立了系统的误差传递模型并计算了由几何误差引入的最大误差。通过与其他几种传统方法进行对比试验，并对螺纹综合测量仪进行测量重复性和测量稳定性分别做了试验。结果表明，该螺纹综合扫描仪的测量精度可靠，同时测量速度更快、参数更齐全。

参考文献

[1]孙玉玖，唐英娜，钱丰.螺纹的综合测量和单项测量[J]．计测技术，2007，27(3)：28-30.

SUN Yujiu，TANG Yingna，QIAN Feng．Measurement of single parameter and synthetical of thread [J]．Metrology & Measurement Technology，2007，27(3)：28-30.

[2]何燕侠，刘振宁．浅析螺纹的几种测量方法[J]．汽车实用技术，2016(4)：127-128.

HE Yanxia， LIU Zhenning. The comparison among several measuring methods of thread [J]. Automobile Applied Technology，2016(4)：127-128.

[3]刘浩，党养正．三坐标测量机测量螺纹量规的一种方法[J]．计测技术，2013，33(1)：29-31.

LIU Hao，DANG Yangzheng. Thread gauge measurement with CMM[J]. Metrology & Measurement Technology， 2013， 33(1)：29-31.

[4]杨慧敏，武军．螺纹量规的多参数测量方法研究[J]．江苏现代计量，2011(3)：53-55.

YANG Huimin，WU Jun. Study on multi-parameter measurement method of thread gauge [J]. Jiangsu Present Day Metrology，2011(3)：53-55.

[5]CARMIGNATO S， CHIFFRE L D. A new method for thread calibration on coordinate measuring machines[J]. CIRP Annals-Manufacturing Technology, 2003，52(1)：447-450.

[6]佟岩，李琳. 螺纹多参数检测的发展方向[J].红外与激光工程，2008，37(S1)：227-229.

TONG Yan，LI Lin. Development of thread multi-parameter measurement [J]. Infrared and Laser Engineering，2008，37(S1)：227-229.

[7]刘力岩，郎岩梅．基于轮廓扫描法的螺纹测量功能的实现[J].机械工程师，2009(8)：142-143.

LIU Liyan，LANG Yanmei. Realization of thread measurement function based on contour scanning method [J]. Mechanical Engineer，2009(8)：142-143.

[8]朱贺贺．高精度接触式螺纹测量仪的误差分析与补偿方法研究[D]．南京：南京航空航天大学，2014.

ZHU Hehe. Errors analysis and compensation of high-precision stylus contact measuring instrument of screw thread[D]. Nanjing ： Nanjing University of Aeronautics and Astronautics，2014.

[9]王秀山，杨建国，闫嘉钰. 基于多体系统理论的五轴机床综合误差建模技术[J]. 上海交通大学学报，2008，42(5)：761-769.

WANG Xiushan，YANG Jianguo，YAN Jiayu. Synthesis error modeling of the five-axis machine tools based on multi-body system theory[J]. Journal of Shanghai Jiaotong Uiversity，2008，42(5)：761-769.

[10]刘启东，徐春广. 基于多体系统理论的车铣中心空间误差模型分析[J]. 组合机床与自动化加工技术，2005(5)：55-58.

LIU Qidong，XU Chunguang. Analysis of volumetric error models for lathe-milling center based on multi-body system theory[J].Modular Machine Tool & Automatic Manufacturing Technique，2005(5)：55-58.