载流圆线圈轴线上磁场理论分布与实测对比分析

侯宏涛，侯双霞

(1.郑州工业应用技术学院 基础教学部，河南 郑州 451150；2.河南省机械设计研究院有限公司，河南 郑州 450002)

载流圆线圈轴线上磁场理论分布与实测对比分析

侯宏涛1，侯双霞2

(1.郑州工业应用技术学院 基础教学部，河南 郑州 451150；2.河南省机械设计研究院有限公司，河南 郑州 450002)

为了研究载流圆线圈轴线上磁场的分布特点，根据毕奥-萨伐尔定律和磁场叠加原理，导出载流圆线圈轴线上磁场分布的表达式。然后，通过实验测出载流圆线圈轴线上磁场分布。将实测值与理论值对比，通过对误差进行分析，得出测准载流圆线圈轴线上测场分布的方法。

圆线圈；轴线；磁场分布；误差

讨论圆线圈轴线上磁场的分布在实际应用中十分有意义。通电圆线圈和亥姆霍兹线圈的磁场分布一直是电磁理论的典型问题，目前已有许多学者[1-3]对圆电流线圈和亥姆霍兹线圈的磁场分布分别从理论推导、实验测量以及数值模拟计算3方面做过大量的研究。

笔者在从事大学物理实验教学过程中，发现很多学生对载流圆线圈轴线上磁场分布理论知识理解不到位、实验操作不熟悉等现象。本文从载流圆线圈轴线上磁场分布的理论推导，以及实验所用仪器、实验测量原理、实验数据处理等方面进行了详细的阐述。最后，通过实验实测出载流圆线圈轴线上磁场分布，并将实测值与理论值对比，通过对误差进行分析，得出测准载流圆线圈轴线上测场分布的方法，用此方法进行测量得到的实验值与理论值非常吻合。

1 载流圆线圈轴线上磁场的理论分布

如图1，设真空中有一半径为R的细载流圆导线，其电流为I。通电圆导线上任一电流元Idl到轴线上P点的矢径r之间的夹角θ均为90°，由毕奥-萨伐尔定律知，该电流元在P点激发的磁感应强度dB的大小[4](P177-182)，[5](P130-133)为

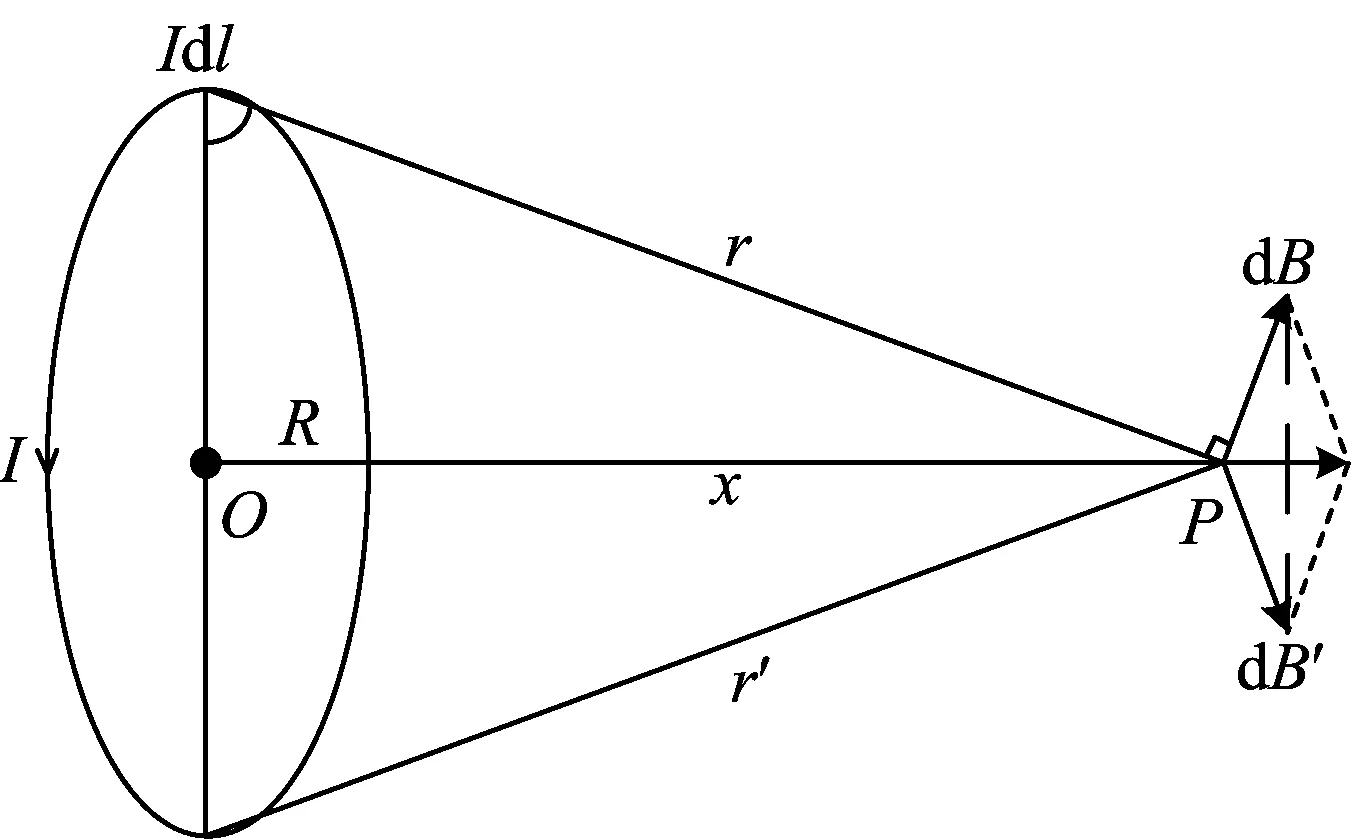
图1 载流圆导线轴线磁场分布

由图知，P点的磁感应强度B沿着轴线方向，大小等于细载流圆导线上所有电流元激发的磁感应强度dB沿轴向方向的分量dB∥的代数和，即

由公式可知，载流圆导线轴线上的磁感应强度随着x的增大逐渐减小，x=0(圆心)处磁感应强度最大。

若一个圆线圈上缠绕N0匝圆导线，此时的载流圆线圈轴线上磁场的大小分布为

式中μ0=4π×10-7H/m,叫做真空的磁导率，N0是载流圆线圈的匝数，R′载流圆线圈的有效半径，x为轴上某一点P到圆线圈中心O′的距离，图2为载流圆线圈轴线上磁场的大小的理论分布。

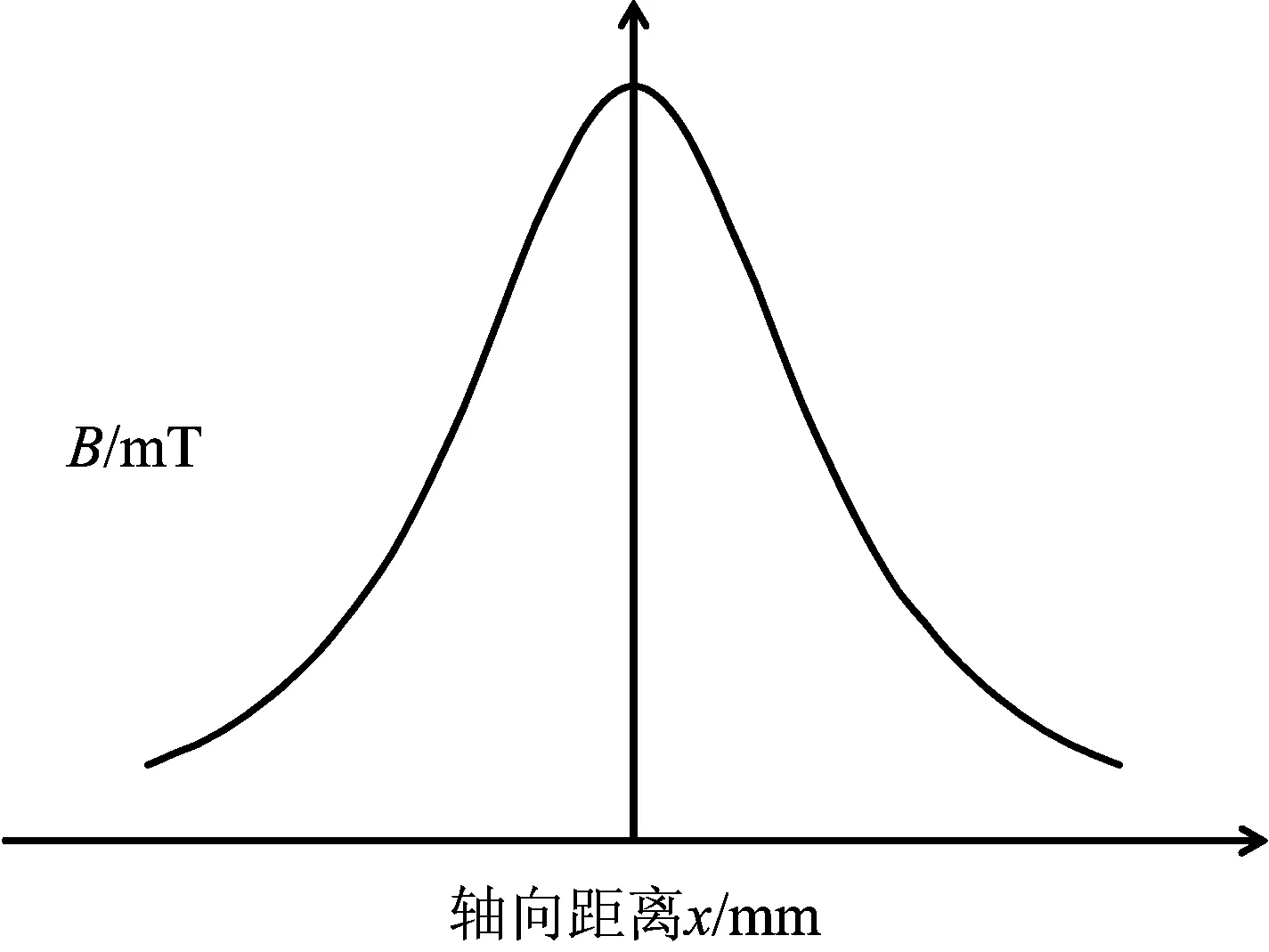
图2 载流圆线圈轴线上磁场的理论分布

2 载流圆线圈轴线上磁场的测量

2.1 实验仪器

(1)DH4501亥姆霍兹线圈磁场实验仪，面板见图3。其中毫伏表用来测量探测线圈的感应电压。

图3 DH4501亥姆霍兹线圈磁场实验仪面板

(2)DH4501亥姆霍兹线圈面板与线圈架分别见图4和图5。

图4 DH4501亥姆霍兹线圈面板

图5 DH4501亥姆霍兹线圈架

亥姆霍兹线圈架主要参数：

二个励磁线圈：线圈有效半径为105mm，单个线圈匝数为400 匝，二线圈中心间距105mm。

移动装置：横向可移动距离260mm，距离分辨率1mm。

探测线圈：匝数1 000，旋转角度360°。

2.2 电磁感应法测量磁场原理

在圆导线中通以频率为f的交流电，线圈将产生交变磁场，如果把一个探测线圈放在这个磁场中，如图6所示。

图6 探测线圈产生感应电动势示意图

探测线圈中将产生的感应电动势，由法拉第电磁感应定律可得，感应电动势的大小为

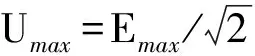
式中，ω=2πf，f为交流电频率，S为探测线圈的面积。

2.3 探测线圈的设计

实验中由于磁场的不均匀性，这就要求探测线圈要尽可能的小。实际的探测线圈又不可能做得很小，否则会影响测量灵敏度。一般设计的探测线圈长度L和外径D有L=2D/3的关系，线圈的内径d与外径D有d≤D/3的关系，尺寸示意如图7所示。

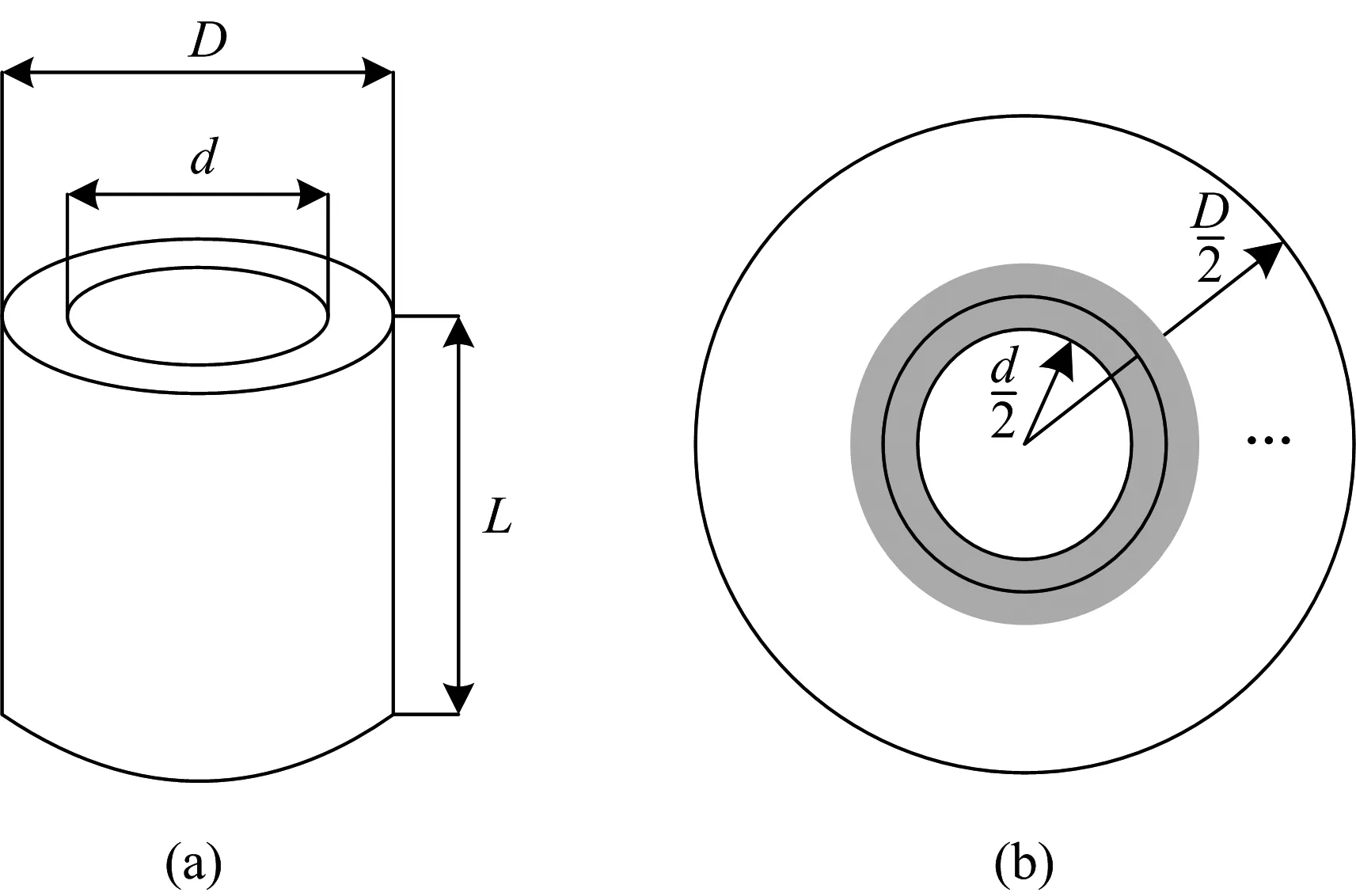
图7 探测线圈及横截面示意图

这样的探测线圈测得的平均磁感应强度可以近似看成是线圈中心点的磁感应强度，经过理论计算得

将不同的频率f代入上式就可得出B值。

2.4 轴线上磁场的测量

调节频率调节电位器，使频率表读数为120 Hz，调节磁场实验仪的电流调节电位器，使励磁电流有效值为I=60 mA，以圆电流线圈中心为坐标原点，每隔10 mm测一个Umax值，测量过程中注意保持励磁电流值不变，并保证探测线圈法线方向与圆电流线圈轴线夹角为0°，将探测线圈从θ=0°转到180°，分别记录0°和180°下Umax值。最后将测量数据记入表1和表2。

表1 0°时载流圆线圈轴线上磁场分布(f=120 Hz，I=60 mA)

表2 180°时载流圆线圈轴线上磁场分布(f=120 Hz，I=60 mA)

3 实测值与理论值对比分析

绘制出表1和表2中载流圆线圈轴线上磁场分布的测量值与理论值曲线，如图8和图9所示。

由图8可以看出，当探测线圈法线方向与圆电流线圈轴线夹角为0°时，实验值均小于理论值，由表1可知，实验值与理论值的最大相对误差为6.5%，误差超过5%，超过实验允许的最大误差。

由图9可以看出，当探测线圈法线方向与圆电流线圈轴线夹角为180°时，实验值均大于理论值，由表2可知，实验值与理论值的最大相对误差为5.6%，误差超过5%，超过实验允许的最大误差。

本实验仪器采用一体化装置，仪器存在系统误差，为了能够更加准确地测出实验值，将探测线圈法线方向与圆电流线圈轴线夹角为0°和180°两种情况下测出的实验值求和取平均值，并将数据记录为表3。

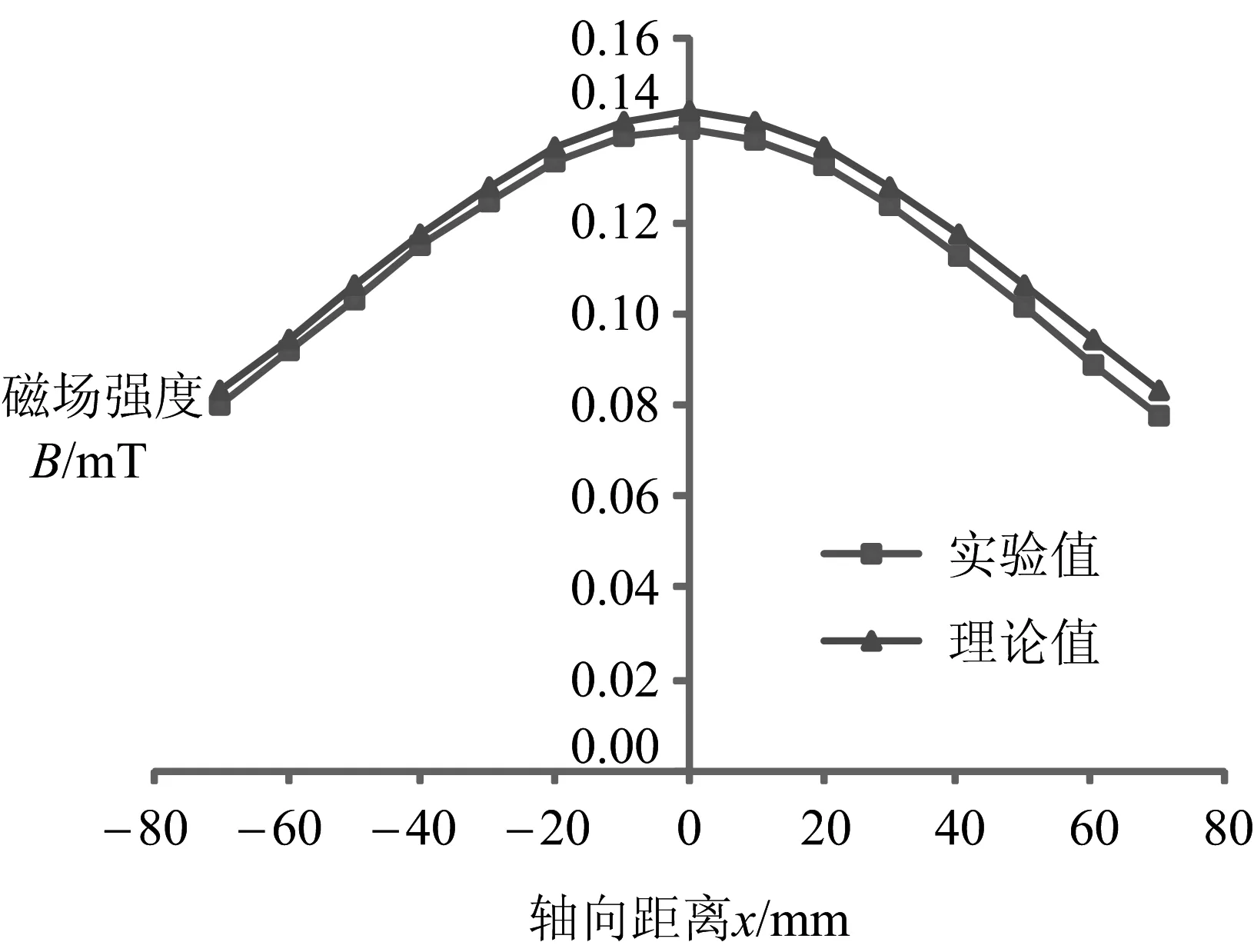
图8 0°时载流圆线圈轴线上磁场分布对比

图9 180°时载流圆线圈轴线上磁场分布对比

轴向距离x/mm-70-60-50-40-30-20-10010203040506070平均值/mT0．0840．0950．1070．1180．1280．1370．1420．1440．1420．1360．1270．1160．1040．0920．081理论值B=μ0N0IR22(R2+X2)3/2/mT0．0830．0940．1060．1170．1280．1360．1420．1440．1420．1360．1280．1170．1060．0940．083相对误差/%1．11．01．00．90．60．50．50．30．00．10．40．91．31．92．5

绘制出表3中载流圆线圈轴线上磁场分布的平均值与理论值曲线，如图10所示。

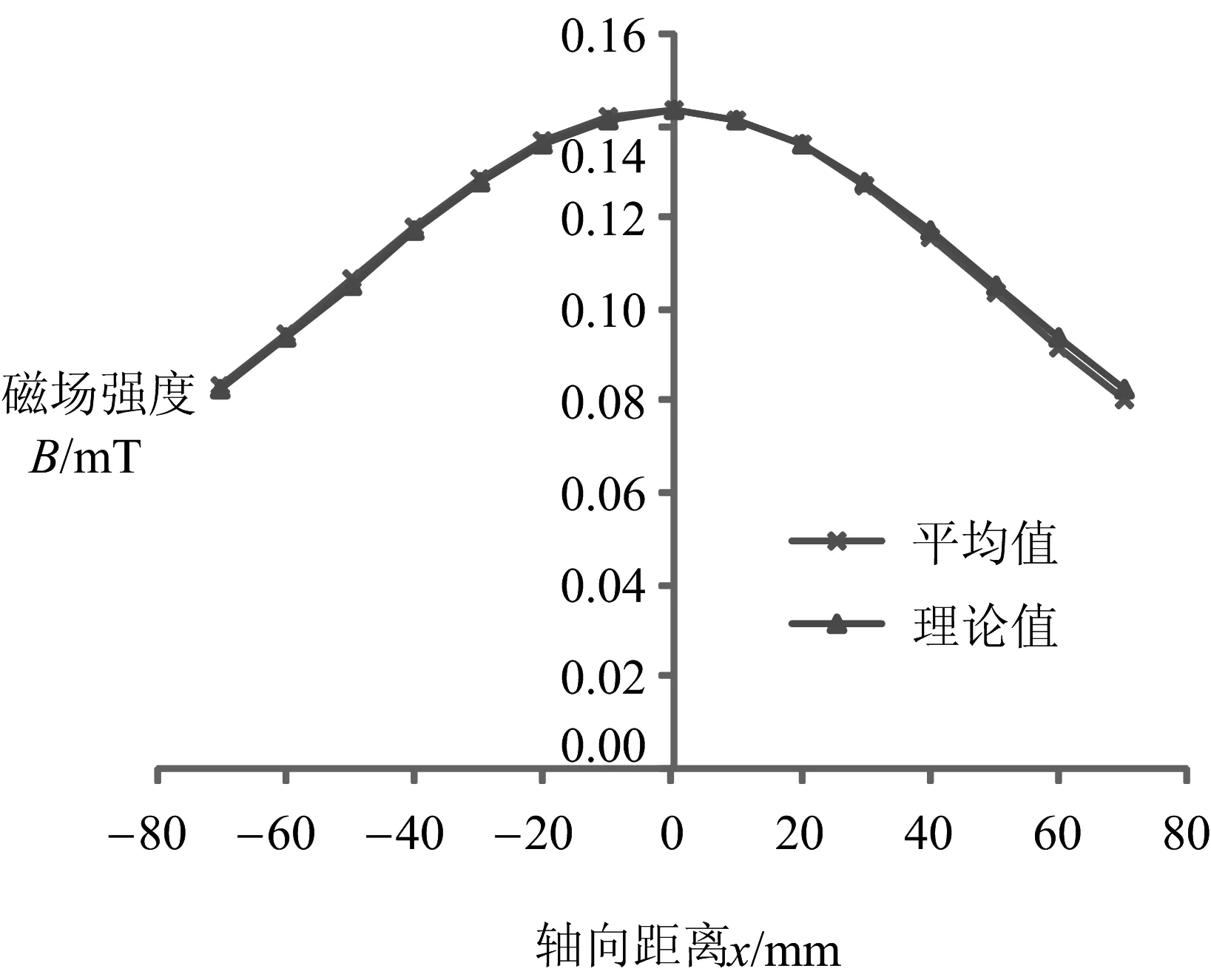
图10 平均值下载流圆线圈轴线上磁场分布对比

由图10可以看出，将探测线圈法线方向与圆电流线圈轴线夹角为0°和180°两种情况下测出的实验值求和取平均值后，此时实验值与理论值吻合的非常好，由表3可知，实验值与理论值的误差均小于5%，最大相对误差为2.5%。

4 结论

通过理论推导和现场实测可以得到如下结论：

(1)理论推导和实验均得出载流圆线圈轴线上磁场的分布，由线圈中心到两端逐渐减小，线圈中心磁场最大。

(2)本实验使用的装置为一体化，使得操作方便，这也使主要实验误差来源于仪器本身，限制了实验可能达到的精度。

(3)探测线圈法线方向与圆电流线圈轴线夹角为0°时，实验值均小于理论值，实验值与理论值的最大相对误差为6.5%。

(4)探测线圈法线方向与圆电流线圈轴线夹角为180°时，实验值均大于理论值，实验值与理论值的最大相对误差为5.6%。

(5)将探测线圈法线方向与圆电流线圈轴线夹角为0°和180°两种情况下测出的实验值求和取平均值后，实验值与理论值吻合的非常好，实验值与理论值的误差均小于5%，最大相对误差为2.5%。

因此，为了能够测出准载流圆线圈轴线上磁场的分布，探测线圈在移动过程中的任意位置，需要分别测出探测线圈法线方向与圆电流线圈轴线夹角为0°和180°两种情况下的实验值，最后再取平均值，可以减小误差，得到的实验数据比较准确。

[1]刘雅洁，朱宁.圆线圈及亥姆霍兹线圈的磁场分布[J].嘉兴学院学报，2004，16(3)：47-50.

[2]张德根，张波.圆电流和亥姆霍兹线圈磁场的数值模拟[J].皖西学院学报，2014，30(2)：39-44.

[3]王青狮，王小伟，邱选兵，等.亥姆霍兹线圈轴线磁场计算机测量实验研究[J].大学物理实验，2010，23(1)：77-85.

[4]梁灿彬，秦光荣，梁竹健，等.电磁学[M].北京：高等教育出版社，2004.

[5]尹国盛，刘学忠.大学物理基础教程[M].北京：机械工业出版社，2016.

[6]刘克涛.多层线圈平均截面积的计算[J].南都学坛(自然科学版)，1992(2)：64-65.

[7]刘克涛，赵桂荣.多层线圈平均截面的另一种计算方法[J].南都学坛(自然科学版)，1993，13(3)：60-61.

A Comparative Analysis of the Theoretical Distribution and Measurementfor Magnetic Field on Circular Current Coil Axis

HOU Hongtao1，HOU Shuangxia2

(1.DepartmentofFundamentalEducation，ZhengzhouUniversityofIndustrialTechnology，Zhengzhou451150，China;2.HenanMechanicalDesignandResearchInstituteCo.Ltd,Zhengzhou450002,China)

In order to study the characteristics of magnetic field distribution on Circular current coil axis, based on the Biot-Savart law and superposition principle of magnetic field, the expression of magnetic field distribution on Circular current coil axis were derived. And then, through experiment we measured the magnetic field distribution on Circular current coil axis. Compared measured values with the theoretical value, through analysis error, to obtain the accurate method of measuring the magnetic field distribution on Circular current coil axis.

circular coil; axis; magnetic field distribution; error

2016-11-19

侯宏涛(1988-)，男，河南洛阳人，助教，硕士研究生，研究方向：大学物理、大学物理实验教学与管理；侯双霞(1985-)，女，河南周口人，硕士，工程师，研究方向：电化学材料的制备、检测，建筑材料成分的分析及烧结砖、瓦的工艺。

O44

A

1009-9735(2017)02-0058-05