平行燃面推移方法在Pro/E软件上的应用*
罗颢文,高凤莲,胡峰,杨敏娟
(西安长峰机电研究所, 陕西 西安 710065)
平行燃面推移方法在Pro/E软件上的应用*
罗颢文,高凤莲,胡峰,杨敏娟
(西安长峰机电研究所, 陕西 西安 710065)
燃面推移的实体造型法与药形结合比较紧密,精度有所保证,可以直观显示不同时刻装药的构型以及面积、体积等相关信息。根据平行层燃烧规律,推导出“点推球,线推管,面平移”的几何推移规律,同时基于Pro/E Wildfire4.0软件的功能应用,介绍了使用Pro/E进行燃面推移的基本假设原则、常用的软件工具以及一般步骤,并进行了实例简介,最终得出结论。
Pro/E Wildfire4.0;燃面推移;实体造型法;平行层燃烧规律;几何推移规律;衍生燃面
0 引言
精确打击是各类武器发展的重要方向,为了满足飞行器外弹道的性能要求,在选定推进剂种类时,主要通过改变推进剂药型,调整燃面变化规律来提供所需推力曲线。因此,精确的燃面变化规律计算是发动机内弹道性能预估以及发动机装药设计品质的基础[1]。同时,如何确定复杂三维药柱的燃面推移规律,为计算模型提供精确的燃面-肉厚数据,也是固体火箭发动机参数辨识技术亟需解决的问题之一[2]。
目前已发展的燃面计算方法主要分为以下几类:解析法、作图法、通用积分法[3]、网格推移法[4]和实体造型法[5]。药柱几何形状的演变过程,是从简单管状药柱演变到贴壁浇注内孔(星形、车轮形等)燃烧药柱,再到具有较高装填特性的翼柱、锥柱等三维药柱[6]。在高性能火箭及导弹需求的牵引下,固体发动机的装药逐渐开始向三维复杂装药和高装填密度方向发展, 传统的燃面计算方法主要针对具有规律性的一维、二维药柱(如圆柱形装药、星空装药等)[7],已很难快捷准确地给出装药燃面变化规律。实体造型法是指利用三维构型分析软件定义装药实心体元素,同时通过“推移”每一燃烧肉厚对应的装药内腔芯模,实心体“减去”芯模就得到对应的装药形状。该方法与药形结构结合比较紧密,具有精度高、形象直观、集成性好等优点[8],同时精度有所保证,可以直观显示不同时刻装药的构型以及面积、体积等相关信息。相比较而言,实体造型法不需要太多的人工计算和数学推导,只需较少的输入,就能得到形象直观、信息完备的输出结果,同时具有良好的继承性和可拓展空间,能设计和计算未来更复杂的三维药柱[9]。
本文结合固体火箭发动机燃面的“平行层燃烧规律”,并基于Pro/E Wildfire4.0软件的功能应用,介绍了通过利用Pro/E三维实体造型软件构造固体发动机装药, 模拟药柱燃面推移过程, 得到药柱燃烧的实时几何体, 从而计算出不同时刻下药柱的几何参数和质量参数的方法。
1 平行层燃烧规律
在19世纪先后由皮奥波特(Piobert)和维也里(Vieille)根据火炮发射中抛出残余药片的形状同原来药片的相似情况,观察并总结了药片燃烧的实践经验,提出了“几何燃烧定律”。其中包括3项基本假设:①整个装药的燃面同时点燃;②装药成份均匀,燃面各点的条件相同;③燃面上的各点都以相同的燃速向装药里面推进。根据这些条件,在燃烧过程中,装药的燃面始终与起始燃面平行,形成“平行层燃烧规律”[10]。
固体火箭发动机装药是以平行层燃烧规律燃烧的, 发动机三维装药上的任何一个燃面都可以看成是组成于该燃面上的点沿其法向进行燃烧推进, 对于装药中任何一点在任何时刻是否燃烧可以通过判断该点距燃面的最短距离来确定[11]。
根据以上燃面变化的基本原理,可以总结出“点推球,线推管,面平移”的几何推移规律。
(1) 点推球
即装药燃面上的所有质点的燃烧规律为,以该质点为球心,以e=rt为半径呈球面状向外推移燃烧,其中e为燃烧肉厚,r为推进剂燃速,t为燃烧时间,见图1。

图1 “点推球”Fig.1 “Points as spheres”
(2) 线推管
即装药燃面上的所有迹线的燃烧规律为,以该迹线为轨迹,以e=rt为半径呈圆管状向外推移燃烧,见图2。

图2 “线推管”Fig.2 “Curves as tubes”
(3) 面平移
如图3a)所示,在t=0时,燃面为Ab(0),结合“点推球”和“线推管”规律,新的燃面是以Ab(0)上各点为球心、以e为半径的所有球面的包迹[3]。故曲面的燃烧规律为曲面向装药内部方向进行“扩张”或“收缩”状的“平移”:直边平移一段距离但长度不变,而圆弧段向装药内部扩张或收缩,即圆心不变, 半径增大或缩小,如图3b)所示。

图3 “面平移”Fig.3 “Surfaces translation”
需要指出的是,以上“点推球,线推管,面平移”的几何推移规律同样适用于“存在于装药内部的燃面”,故亦可拓展应用于有内部缺陷的装药燃面推移等,参考文献[12]中介绍了利用实体造型法进行含裂纹的固体火箭发动机性能分析的例子。
2 Pro/E燃面推移常用工具
Pro/E是基于参数化、全相关、特征设计思想的主流CAD三维设计软件[13],其基于特征、全尺寸约束、尺寸驱动设计修改及全数据相关等特点使得发动机装药设计(尤其是三维复杂药型装药)更加方便, 效率更高, 燃面计算更加准确、直观[14]。
使用Pro/E进行实体造型法燃面计算的基本思想是将整个燃面看作被插曲面, 对被插曲面进行计算插值, 计算出被插曲面插值的数据点, 将每一个点沿其法向推进一个位移, 距离与当地的燃速成正比, 得到该节点在下一个时刻的位置, 由这些点所构造的插值曲面即为新燃面[15]。
Pro/E比较全面的三维构型和参数提取工具,在使用Pro/E软件进行燃面推移时,常用的工具可以分为“与初始燃面建立有关”、“与新燃面状态下装药构型有关”及“与分析参数建立有关”3类。
2.1 与初始燃面建立有关的工具
进行燃面推移时需建立初始的燃面。
可以在初始时就建好完整的装药初始构型,即装药的外形及内孔均完整构建出,再将装药实体上的所有初始燃面选中复制出。
但建议将初始的燃面独立于药柱外型单独进行构建避免出错。构建初始燃面的工具主要即为Pro/E常见的曲面建构工具,例如拉伸、旋转、扫描、混合、扫面混合及可变剖面扫面等。
2.2 与新燃面状态下装药构型有关的工具
在新状态下的燃面需要在初始燃面的基础上进行构建,即通过偏移工具将初始燃面偏移需要的肉厚得到相应的新燃面。但应注意,当部分燃面在推移时,会出现新的“衍生燃面”,在构建“衍生燃面”时应时刻遵守“点推球,线推管,面平移”的原则,如图4所示。

图4 衍生燃面Fig.4 Derived burning areas
2.3 与分析参数建立有关的工具
建立了新状态下的装药构型后,需要将燃面面积以及燃烧肉厚等建立为具体的参数并将其提取出来,才能进行推移和分析计算。燃面特征的参数中必定有相应的代数关系,需要在“关系…”中编写这些参数的代数关系。
常使用“区域”工具进行面积测量并提取面积参数,并使用“分析”特征建立新的局部参数代表所有的局部燃面之和,并编写相应关系式。
可以使用“敏感度分析”工具进行燃面的推移计算,同样也可以用其计算装药质量、质心等其他特性随燃面推移的变化趋势。
3 燃面推移常用步骤
使用Pro/E进行燃面推移的一般主要分为“建立装药外型”、“建立初始燃面元素”、“建立新燃面”、“建立参数化关系”以及“进行敏感度分析计算”5个步骤。
3.1 建立装药外型
首先应将整个装药的外型构建出,注意所构建的实体应包含装药所有的非燃面。
由于绝大多数装药(外型及燃面)具有一定的对称性,可根据实际情况考虑只构建部分装药外型,这能大大简化后续的工作。
3.2 建立初始燃面元素
在装药外型建立后需建立与燃面有关的特征元素。可以将燃面分解为多个简单的几何元素,方便后续的偏移工作,同时也减少出错的几率。
例如图5中a)所示的药型为2段直径不同的圆管内孔、中间使用一段圆锥进行过渡的药型。可直接使用旋转工具将整个燃面进行构建如图5b)所示;但根据“点推球,线推管,面平移”原则,在大圆孔与圆锥相接部位应构建圆弧状的衍生燃面,如图5c)中所示,随着衍生燃面的扩大以及锥段燃面的退化,可能由于锥段燃面消失而出现报错;故可将燃面分解为一个小圆孔的管段和一个由大圆孔段和锥段共同组成的变截面管段以避免该种错误,如图5d)所示。
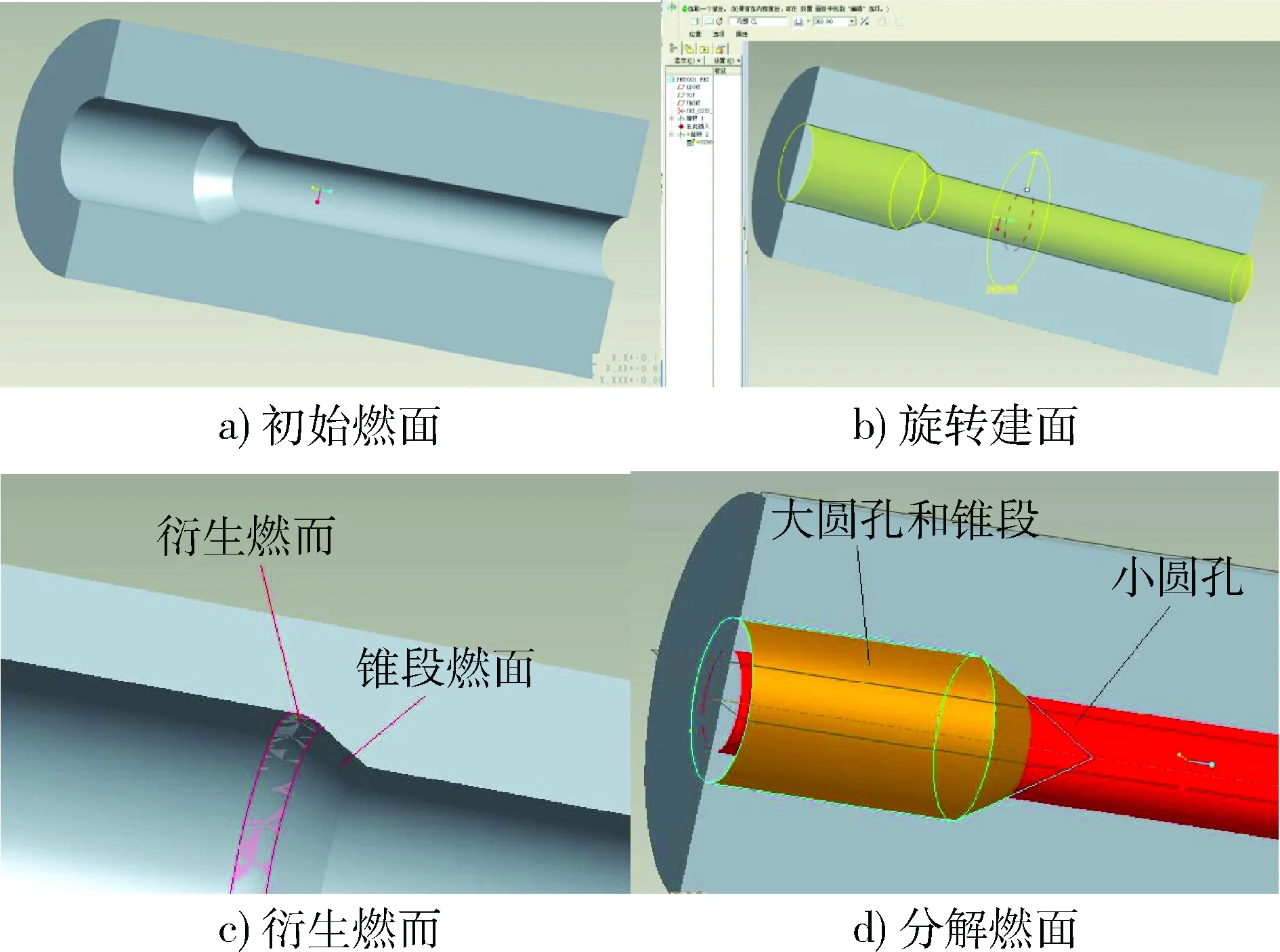
图5 初始燃面的建立Fig.5 Building initial burning areas
有时由于某些局部燃面在推移到一定时候的退化消失或其他原因,软件可能报错,例如某些呈收缩趋势的圆角,如图6。可以考虑在不影响计算精度的前提下将其简化甚至省略。

图6 呈退化消失趋势的燃面Fig.6 Degrading burning areas
有时为了作一些特殊计算,可将一些特殊的燃面进行等效,例如参考文献[16]中介绍了利用多个球形模型进行含弯曲金属丝的端燃药柱燃面计算的例子。
3.3 建立新燃面
新燃面的建立主要依靠初始燃面的偏移,但应当注意结合 “点推球,线推管,面平移”原则判断新产生的衍生燃面。
有的衍生燃面需要在偏移后的燃面上作一定的处理,例如图5c)所示的衍生燃面,可在偏移后的大圆弧和锥段的衔接处进行倒圆角处理,圆角的半径即为燃烧的肉厚,如图7所示。
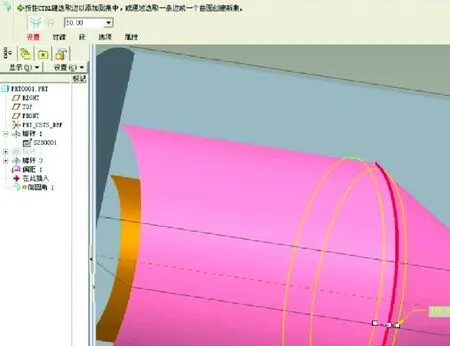
图7 在偏移后的燃面上处理出的衍生燃面Fig.7 Derived burning areas built on offset burning areas
有的衍生燃面则可以考虑采用其他工具来获得,如图5所示的衍生燃面,可以通过扫描工具直接去除材料获得,如图8所示。
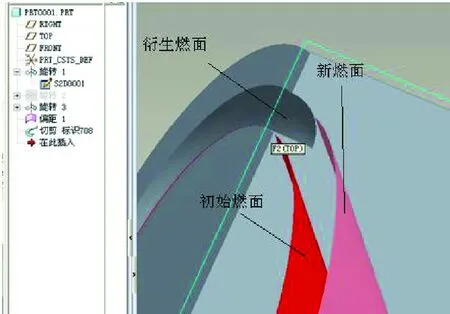
图8 通过去除材料获得的衍生燃面Fig.8 Derived burning areas built by removing material
构建好完整的新燃面后即可以通过实体化工具去除材料获得新燃面状态下的装药构型。
3.4 建立参数化关系
构建好的新燃面状态下装药构型是“静态”的,各特征元素之间相对“独立”没有实质关联,需进一步建立各个特征与某一统一参数之间(通常为燃烧肉厚)的关系。
如2.3中所述,可使用“区域”工具进行面积测量提取出面积参数,并通过 “分析”工具建立一个分析特征,在其中建立新的局部参数并编写相应关系式。
有时装药的非燃面组成比燃面组成更简单,故也可以考虑采用计算总面积与非燃面面积之差求出装药燃面面积的方法。
3.5 进行敏感度分析计算
此时即可利用“敏感度分析”工具进行燃面的推移计算,将“变量选取”选择为最初定义为燃烧肉厚的尺寸或参数(自变量),“变量范围”选择为所需的肉厚变化范围,“出图用的参数”选择为代表所有燃面面积之和的参数(因变量),再选择合适的计算步数使计算的肉厚间隔满足使用需求,即可开始得到燃面面积随肉厚变化的曲线,见图9。也可将因变量选择为装药质量、质心等其他参数,以获得其随肉厚变化的曲线。
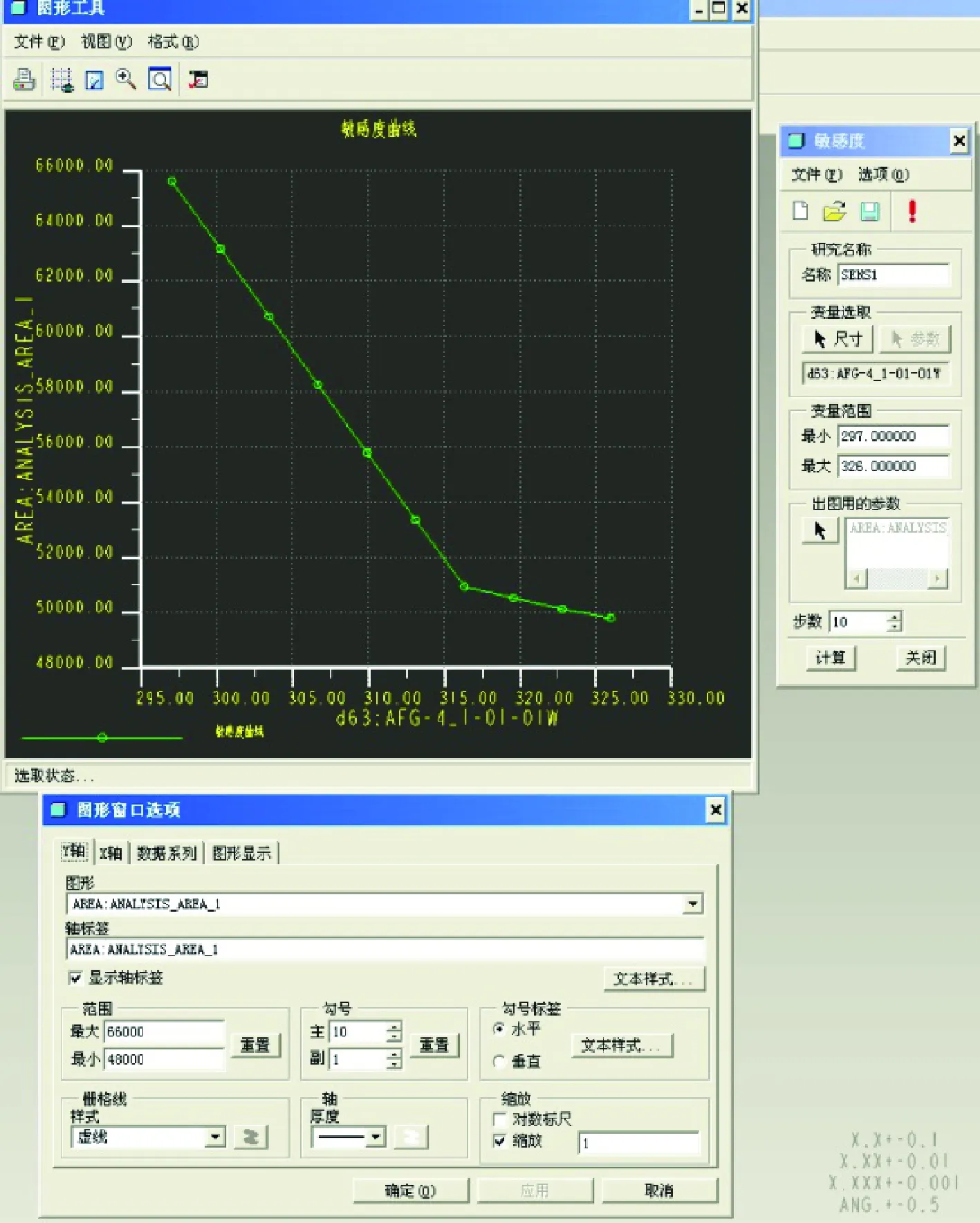
图9 敏感度分析Fig.9 Sensitivity analysis
这里需要指出的是,有时由于药型燃面特点,衍生燃面会出现推移的过程中而不是初始时期,如图10,此时需要考虑分阶段构建燃面及推移肉厚。

图10 推移过程中出现的衍生燃面Fig.10 Derived burning areas appear during developing
4 实例分析
星孔药型药柱是常用的药柱结构之一,其燃面的结构比较复杂,在星角直边消失之前存在多个直纹面,在星尖圆弧半径消失之后的燃面上有多条脊线[17]。
根据3中所介绍的步骤,对一个典型的星孔药型药柱进行推移,主要药型几何参数见表1。
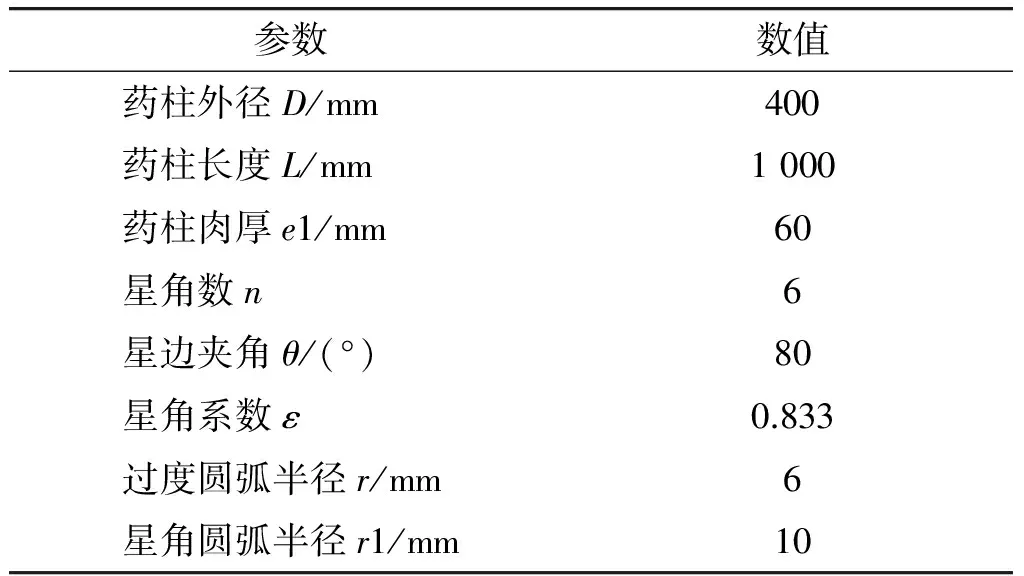
表1 示例药型参数
主要燃面推移计算步骤如下(见图11):
(1) 建立该药柱外型,即为一个直径400 mm、长1 000 mm的圆柱,根据对称性,选择简化计算其1/12部分;
(2) 建立初始燃面,星角底部的圆弧呈退化趋势并会很快消失,故将其简化为普通直边;
(3) 将初始燃面进行一定的偏移,这里没有衍生燃面的产生,故可直接使用实体化工具去除新燃面包络内部的装药部分;
(4) 提取出燃面参数,该药型燃面主要包括星顶圆弧、过度圆弧和星边直段3个部分,提取出各部分的面积参数后再在分析工具中建立局部参数求出各部分之和;
(5) 在敏感度分析工具中,将变量选取为偏移的尺寸量,出图参数选项选为燃面面积之和,选择需要的变量范围(肉厚计算范围)和步数(计算点数据个数),即可进行偏移计算。
最终计算结果见图11g),将(简化了根部圆角和没有简化的)计算结果与使用解析法得出的结果进行对比,简化了星角倒圆的结果与未进行简化的结果最大差距为3.26%,最大误差出现在初始时刻,是由于简化处理的直线段长度比原圆弧长;对方案论证初期,该误差可接受,且在侵蚀性能还不确定情况下,计算初始压强会偏高一些,发动机设计会偏于安全。
若星角圆弧较大或药柱长度较长使简化后的误差大于要求范围,在精确工程设计时,可考虑在星角倒圆消失前后分开建模。未简化星角倒圆的计算结果与解析法计算结果最大差距仅为0.009 7%。

图11 实例演示Fig.11 Example demonstration
同时可以将质心参数提取出,并将敏感度分析工具中出图参数同时选中燃面面积和质心参数,就可以同步进行二者随燃烧肉厚变化的趋势,见图11h)。
5 结束语
根据“平行层燃烧规律”的基本原理,可以推导出遵守“点推球,线推管,面平移”的燃面推移规律,据此使用基于Pro/E的实体造型法,造型方便, 效率更高, 燃面计算更加准确,同时可以直观显示不同时刻装药的构型以及面积、体积等相关信息。
[1] 马长礼.固体火箭发动机MDF燃面计算方法研究[D].长沙:国防科学技术大学,2007. MA Chang-li. Research of MDF Burning Surface Calculation Method for Solid Rocket Motor[D]. Changsha: National University of Defense Technology, 2007.
[2] 魏瀚,鲍福廷,蔡强,等.固体火箭发动机参数辨识软件关键技术研究[J].科学技术与工程,2011,11(36):9016-9020. WEI Han, BAO Fu-ting, CAI Qiang, et al. Research on Enabling Techniques for Identification Software for Solid Rocket Motor Model Parameters[J]. Science Technology and Engineering, 2011,11(36):9016-9020
[3] COATS D E, LEVINE J N, COHEN N S, et al. A Computer Program for the Prediction of Solid Propellant Rocket Motor Performance[R].Vol.ⅠⅡandⅢ, AFRPL-TR-75-36.
[4] BRETON P L, RIBEREAU D, GODFROY F, et al. SRM Performance Analysis by Coupling Bi-Dimensional Surface Burnback and Pressure Field Computation[R]. AIAA98-3968.
[5] 秦飞.固体火箭发动机复杂装药燃面算法研究[D].西安:西北工业大学,2003. QIN Fei. Method Research for Burning Surface Calculation of Solid Rocket Motor with Complicated Grain[D]. Xi’an: Northwestern Polytechnical University, 2003.
[6] 王磊,代义,李宏. 基于Pro/E软件进行固体火箭发动机内弹道计算的方法初探[J].中国新技术新产品,2009(10):8-9. WANG Lei, DAI Yi, LI Hong. A Preliminary Study of Solid Rocket Motor Internal Ballistic Calculation Method Based on Pro/E Software[J]. China New Technologies and New Products, 2009(10):8-9.
[7] 赵新平. 固体火箭发动机装药燃面集成计算方法研究[D]. 南京:南京理工大学,2007. ZHAO Xin-ping. The Research into the Method of Solid Rocket Motor Burning Surface Calculation[D]. Nanjing: Nanjing University of Science and Technology, 2007.
[8] 蔡强,鲍福廷. 基于ACIS几何造型平台的固体火箭发动机装药设计[J].固体火箭技术,2008,31(3):236-238,242. CAI Qiang, BAO Fu-ting. Grain Design of Solid Rocket Motor Based on Acis Geometric Modeling Platform[J]. Journal of Solid Rocket Technology,2008, 31(3): 236-238, 242.
[9] 葛爱学, 夏智勋, 方丁酉. 固体火箭发动机三维药柱燃面计算方法的分析与比较[J].战术导弹技术,1999(3): 34-38. GE Ai-xue, XIA Zhi-xun, FANG Ding-you. Analysis and Comparison of Calculating Methods of 3-D Grain Burning Surface in Solid Rocket Motor[J]. Tactical Missile Technology,1999(3):34-38.
[10] 李宜敏,张中钦,张远君.固体火箭发动机原理[M].北京:北京航空航天大学出版社,1991:167. LI Yi-min,ZHANG Zhong-qin,ZHANG Yuan-jun.Solid Rocket Engine Principle[M].Beijing:Beihang University Press,1991:167.
[11] 熊文波,刘宇,任军学,等. 基于单元法的三维装药通用燃面计算[J].航空学报,2009,30(7):1176-1180. XIONG Wen-bo, LIU Yu, REN Jun-xue, et al. Generalized Burning Surface Calculation of Three Dimensional Propellant Based on Element Method[J]. Acta Aeronautica et Astronautica Sinica, 2009,30(7):1176-1180.
[12] 费阳.含裂纹固体火箭发动机性能分析[D].长沙:国防科学技术大学,2010. FEI Yang. Analysis on the Performance of Solid Rocket Motor with Cracked Propellant Grain[D]. Changsha: National University of Defense Technology, 2010.
[13] 赵建勋,代菊英,黎聪. 基于Pro/E的简单机构运动仿真及应用[J].机械制造与自动化,2012(1):128-130. ZHAO Jian-xun, DAI Ju-ying, LI Cong. Motion Simulation and Application of Simple Mechanism Based on Pro/Engineering[J]. Jiangsu Machine Building & Automation,2012(1):128-130
[14] 马亮,杨德敏,王瑾,等. 基于Pro/E的含金属丝双推力药柱燃面计算方法[J].弹箭与制导学报, 2008,28(2):143-145. MA Liang, YANG De-min, WANG Jin, et al. Burning Area Calculation of Dual Thrust Grain with Metal Wires Based on Pro/E Software[J]. Journal of Projectiles, Rockets,Missiles and Guidance,2008,28(2):143-145.[15] 于胜春,赵汝岩,周红梅,等. 基于Pro/E特征造型技术的固体发动机装药燃面计算[J]. 固体火箭技术,2005,28(2):108-111. YU Sheng-chun, ZHAO Ru-yan, ZHOU Hong-mei, et al. Burning Area Regression Simulation and Calculation of Solid Rocket Motor Grains Based on Pro/E Feature Modeling Technology[J]. Journal of Solid Rocket Technology, 2005,28(2):108-111.
[16] 孙兵. 含金属丝端燃药柱中金属丝弯曲情况下发动机内弹道性能计算分析方法[C]∥中国宇航学会固体火箭推进专业委员会第二十一届年会固体火箭推进技术学术会议,上海,2004,10. SUN Bing. The Internal Ballistic Performance Calculating and Analyzing of End-Burning Grain with Bended Metal Wire[C]∥China Aerospace Society of Professional Committee of the Solid Rocket Propulsion Solid Rocket Propulsion Technology, the 21st Annual Meeting of Academic Conference Proceedings, Shanghai, October, 2004,10.
[17] 陈步学,王凌燕,吴心平. 星孔装药燃面退移图象显示中的特殊问题[J]. 推进技术,1997,18(4):46-50. CHEN Bu-xue, WANG Ling-yan, WU Xin-ping. Special Problems on Graphic Display of Burning Surface Regression of Star Perforation Grains[J]. Journal of Propulsion Technology, 1997,18(4):46-50.
Parallel Burning Area Process Method Application on Pro/E Software
LUO Hao-wen, GAO Feng-lian, HU Feng, YANG Min-juan
(Xi’an Changfeng Institute of Electrical and Mechanical,Shaanxi Xi’an 710065, China)
When used in burning area calculation, solid modeling method is closely combined with grain structure, so that the accuracy can be guaranteed. Besides, the grain structure, area, volume and some other relevant parameters can be intuitively displayed at different time. According to the law of propellant burning in parallel layers, this passage deduces the law of geometrical evolution as “points as spheres, curves as tubes and surfaces translation”, besides, based on the application of Pro/E Wildfire 4.0 software, this passage introduces the basic assumptions and principles, common tools and general steps of burning area calculation using Pro/E software, giving an example, and finally arriving at conclusions.
Pro/E Wildfire 4.0; burning area calculation; solid modeling method; parallel layers burning law; geometrical evolution law; derived burning area
2016-05-08;
2016-07-22 作者简介:罗颢文(1989-),男,四川泸州人。学士,助工,主要从事总体设计工作。
10.3969/j.issn.1009-086x.2017.02.032
V435;V51;TP391.9
A
1009-086X(2017)-02-0202-07
通信地址:710065 陕西西安电子一路8号长峰机电研究所发动机研究中心一室 E-mail:283602682@qq.com

