小推质比条件下Lambert制导方法的快速修正*

杏建军，陈子昂，石凯宇，廖俊

(1. 中南大学 航空航天学院， 湖南 长沙 410083; 2. 北京电子工程总体研究所， 北京 100854)

小推质比条件下Lambert制导方法的快速修正*

杏建军1，陈子昂1，石凯宇2，廖俊1

(1. 中南大学 航空航天学院， 湖南 长沙 410083; 2. 北京电子工程总体研究所， 北京 100854)

针对Lambert速度冲量制导方法小推质比实施误差较大的问题，提出了一种解析的快速修正方法。该方法以Lambert速度冲量制导终端状态为约束条件，采用修正初始制动点的方式修正小推质比实施速度冲量带来的误差。仿真结果表明：该方法可有效修正速度冲量假设小推质比实施的误差，并且具有计算量小、速度快的优点。

Lambert制导；速度冲量；有限推力；小推质比；线性化方法；解析修正

0 引言

在已知飞行器初始和终端位置矢量的条件下，Lambert速度冲量制导方法可以快速设计出连接这2个点的最优转移轨道和速度冲量施加方式[1-2]，并具有固定飞行时间、固定飞行再入角和最小转移能量等多种变化形式，因此被广泛地应用于大气层外的飞行器轨道机动中，如空间交会对接[3-4]、行星探测轨道转移[5-6]、空间卫星拦截[7]、飞行器再入[8]等。

Lambert方法是一种基于二体动力学假设的速度冲量制导方法，在实际实施中具有较大的误差，特别是速度冲量假设。在大气层外，速度冲量制导方法有限推力实施时，会带来重力损失[9]：当飞行器推力较大，推质比达到5～10时，速度冲量假设带来的误差可以忽略；当飞行器推力较小，推质比为0.5～1时，速度冲量假设带来的误差不可忽略。由于重力损失与飞行路径角有关，一般通过数值积分或数值优化的方法修正[10-12]，数值计算的方法具有精度高，适应面广的优点，但也有计算量大的缺点，不适合在星上计算资源比较紧张的任务中使用。

针对Lambert速度冲量制导方法有限小推质比实施误差大，数值修正计算量大的问题，提出了一种解析的修正方法。该方法首先分别将速度冲量与有限推力作用下飞行器飞行轨迹沿一个虚拟的圆轨道进行线性化；其次根据线性化的方程求解2种方式飞行轨迹的解析解；最后通过调整有限推力作用初始点的位置和速度，使得2种方式预测的飞行轨迹在有限推力结束后交会(即以相同飞行时间和速度到达空间同一点)，修正速度冲量有限推力实施的误差。

1 基本思路

速度冲量制导有限推力实施时的误差修正如图1所示：设O点为制导方法计算的速度冲量施加点，黑色实线椭圆为速度冲量作用下飞行器飞行轨迹，黑色点划线圆为以地心到O点的距离r1为半径的虚拟圆轨道，其轨道角动量方向与速度冲量作用下飞行器飞行轨迹一致；O1点为飞行器在有限推力作用下实际的制动点，黑色虚线为飞行器在有限推力作用下的飞行轨迹。为了消除速度冲量制导与有限推力实施之间的误差，要求飞行器在同样的飞行时间，速度冲量飞行轨迹与有限推力飞行轨迹在P点交会，飞行器后续沿着速度冲量飞行轨迹飞行。这样，速度冲量制导的有限推力修正就转换成一个以O1点的位置和速度为设计初值，以P点的位置速度为终端约束的固定时间边值问题。

图1 速度冲量有限推力实施修正示意图Fig.1 Method to correct the error between the finite burn and the impulsive (schematic)

2 数学模型

2.1 坐标系

引入2个坐标系：

(1) 描述飞行器绝对运动的地心赤道惯性坐标系(ECI)：坐标原点在地心，x轴指向春分点，z轴指向地球北极，y轴在赤道平面内，由右手定则确定。

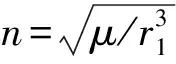
2.2 速度冲量模型

速度冲量飞行轨迹与虚拟圆轨道运动的误差，在虚拟圆轨道RIC坐标系中可表示为(c-w方程)[13-14]

ρ0=(x0,y0,z0)T=(0, 0, 0)T，

(1)

式中：

Av0-(0,nr1,0)T+AΔv，

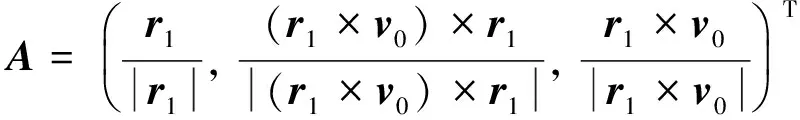
(2)

式(1)是一个线性常微分方程组，有解析解：

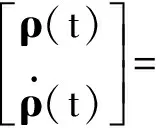
(3)

式中：

2.3 有限推力模型

有限推力作用下，飞行器相对于虚拟圆轨道RIC坐标系中的相对运动方程为[15]

ρ10=(x10,y10,z10)T,

(4)

(5)

式(4)也是一个线性常微分方程组，其解析解为

(6)

式中：

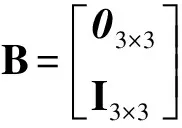
2.4 有限脉冲修正模型

在P点，速度冲量飞行轨迹与有限推力飞行轨迹交会，则

(7)

在式(7)左右各左乘Φ(-t)，则

(8)

又因为Lambert制导方法计算的速度冲量AΔv与有限推力满足如下等式关系

(9)

式中：t为有限推力作用时间。

则有限推力再入点修正为

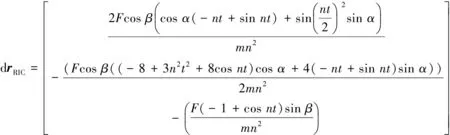
(10)

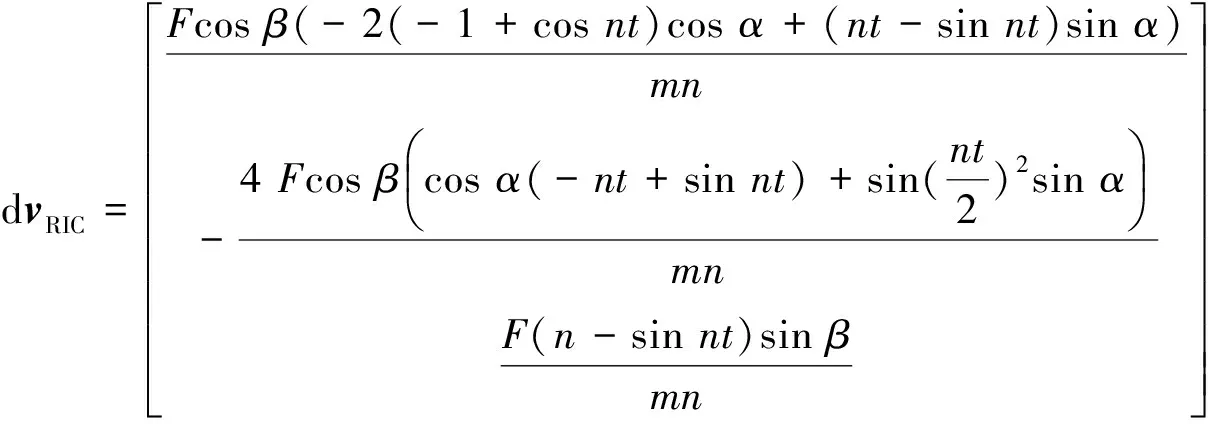
(11)

有限推力制动点在地心惯性坐标系中的位置矢量和速度矢量为

(12)

(13)

3 仿真验证

仿真初始条件：飞行器从381 km的圆轨道返回，制动点在地心惯性坐标系中的位置矢量为(-196.9, -6 296.4 ,-2 449.8) km，速度矢量为(5.972 7, -1.911 3, 4.432 5) km/s，再入大气层的位置矢量为(4 962,-21,4 250) km，再入角为-5°。

3.1 不同推质比下Lambert制导的误差

根据给定的仿真条件，Lambert制导的结果为：在制动点施加的速度冲量为548.88 m/s，制动方向α为120.53°，β为0°,飞行器飞行时间为1 697.20 s。采用不同推质比的发动机进行有限推力实施，在发动机工作期间，制动方向不变，表1给出了仿真结果。

由表1中数据可知，速度冲量大小一定的情况下，推质比越小，飞行器重力损失越大，飞行器轨道机动误差越大。在本算例中，飞行器再入点位置与再入角误差，与飞行器推质比的倒数近似成正比关系，如推质比为20 m/s2时，再入角误差为0.03°，推质比为10 m/s2时，再入角为0.06°，近似满足关系

(14)

当飞行器推质比为1时，有限推力实施的位置误差为百公里量级，飞行器再入角误差接近0.9°。

3.2 有限推力修正后Lambert制导的误差

采用与3.1中同样的仿真条件和Lambert制导结果，用推质比为1的发动机进行有限推力实施，在发动机工作期间，制动方向保持不变。表2给出了不采用有限推力修正和采用本文提出的有限推力修正的仿真结果。

表1 不同推质比下Lambert制导方法有限推力实施的误差

表2 推质比为1时无修正与有修正的误差

由表2中数据可知，采用有限推力修正，再入点为位置精度可从百千米量级提高到20 km量级，再入角误差从0.9°提高到0.15°，二者的制动脉冲完全一致，不会多消耗飞行器的推进剂。

相对于标称制动点的修正参数(地心惯性坐标系)：dr=(-15.312 8，-142.627 2，-64.805 2)km, dv=(-134.98, 158.49, -58.41)m/s。

4 结束语

针对Lambert速度冲量制导小推力实施时误差较大的问题，采用沿虚拟圆轨道线性化的思路，给出了一种解析的修正方法，与数值方法相比，该方法具备计算量小，沿用Lambert制导结果的优点。该方法具有一定的普适性，可用于任意速度冲量制导有限推力实施的误差修正中，也可以用于其他摄动力，包括地球J2项摄动等的修正。

[1] NELSON S L. Alternative Approach to the Solution of Lambert’s Problem[J].Journal of Guidance，Control and Dynamics，1992，15(4)：1003-1009.

[2] SOFAIR I．Application of the Lambert Problem to Inverse-Square Gravity[R]．AD—A451778.

[3] PRUSSING J E, CHIU J H. Optimal Multiple-Impulse Time-Fixed Rendezvous Between Circular Orbits [J]. Journal of Guidance, Control, and Dynamics, 1986, 9(1): 17-22.

[4] 韩潮，谢华伟. 空间交会中多圈Lambert变轨算法研究[J]. 中国空间科学技术, 2004, 24(5): 9-14. HAN Chao, XIE Hua-wei. Research on Algorithm of Loopy Lambert Transfer in Space Rendezvous[J]. Chinese Space Science and Technology, 2004, 24(5): 9-14.[5] 李桢. 载人火星探测任务轨道和总体方案研究[D]. 长沙：国防科技大学，2011. LI Zhen. Study on Trajectory and Overall Scheme Manned Mars Exploration Mission [D]. Changsha:National University of Defense Technology，2011.

[6] 何巍，徐世杰.地一月低能耗转移轨道中途修正问题研究[J]．航天控制，2007，25(5)：22-27. HE Wei，XU Shi-jie. Study on Midcourse Correction of Low Energy Consumption Earth-Moon Transfer Orbit[J].Aerospace Control，2007，25(5)：22-27.

[7] 张鹏宇.空间拦截最优轨道设计[D].哈尔滨：哈尔滨工业大学，2009. ZHANG Peng-yu. Optimal Trajectory Design for Space Interception [D]. Harbin: Harbin Institute of Technology, 2009.

[8] 刘一擎. 天基拦截与对地再入段轨迹优化与制导方法研究[D]. 哈尔滨:哈尔滨工业大学，2015. LIU Yi-qing. Space-Based Interception Trajectory Optimization and Ground-Attacking Reentry Stage Guidance Methods Research [D]. Harbin: Harbin Institute of Technology, 2015.

[9] VLADIMIR A C. Orbital Mechanics[M]. 3rd ed. AIAA, 2002.

[10] 周须峰，唐硕. 固定时间拦截变轨段制导的摄动修正方法[J]. 飞行力学, 2006, 24(4):46-49. ZHOU Xu-feng, TANG Shuo. Disturbed Modify Method of Fixed-Time Interception’s Guidance in Orbit-Change Stage [J]. Flicht Dynamics, 2006, 24(4):46-49.

[11] 李艳艳,任凌.地球同步卫星的小推力离轨最优控制[J]．系统仿真学报，2010，22(1)：96-98． LI Yan-yan，REN Ling．Optimal Low-Thrust Control for Geosynchronous Satellite Deorbit[J]．Journal of System Simulation，2010，22(1)：96-98．

[12] 袁宴波，李东伟．天基对地打击武器最优过渡轨道研究[J]．科学技术与工程，2009，9(6)：1146-1149. YUAN Yan-bo，LI Dong-wei．Transition Orbit Optimization Research of Space-to-Ground Kinetic Weapon[J]．Science Technology and Engineering，2009，9(6)：1146-1149．

[13] SABOL C, BURNS R, MCLAUGHLIN C A. Satellite Formation Flying Design and Evolution [J]. Journal of Spacecraft and Rocked, 2001, 38(2): 270-278.

[14] XING J J, TANG G J, XI X N. Satellite Formation Design and Optimal Station Keeping Considering Nonlinearity and Eccentricity[J]. Journal of Guidance, Control and Dynamics, 2007, 30(5): 1523-1528.

[15] INALHAN G, TILLERSON M, HOW J P. Relative Dynamics and Control of Spacecraft Formation in Eccentric Orbits [J]. Journal of Guidance, Control, and Dynamics, 2002, 25(1): 48-59.

Analytical Method to Correct the Lambert Impulsive Guidance Errors under Small Thrust to Mass Ratio

XING Jian-jun1, CHEN Zi-ang1, SHI Kai-yu2, LIAO Jun1

(1. Central South University, College of Aeronautics and Astronautics, Hunan Changsha 410083, China; 2. Beijing Institute of Electronic System Engineering, Beijing 100854, China)

If the thrust to mass ratio is small, the error between the finite burn transfers and the Lambert impulsive guidance is significant. The general method of solution is to run an integrated trajectory computer program. An analytic method is presented to reduce this error and alleviate on-board computer burden. The terminal state parameters of the Lambert impulsive guidance are used as the terminal constraints of the finite burn transfers. The initial state of the finite burn transfers as the design parameters are selected by the linearized method to meet the terminal constraints and make the same trajectory of the finite burn and impulsive transfers after the finite burn. The numerical simulation illustrates the presented analytical method could effectively correct the error of the velocity impulse assumption, and has the advantages of small computation burden.

Lambert guidance; impulse maneuvers; finite thrust; small thrust to mass ratio; linearized method; analytical correct

2016-09-25；

2016-12-12 基金项目：有 作者简介：杏建军(1975-)，男，甘肃兰州人。副教授，博士，主要研究方向为飞行器动力学建模与仿真，飞行器轨迹优化，飞行器轨道确定与预报；编队卫星动力学与控制。

10.3969/j.issn.1009-086x.2017.02.001

TJ765.3

A

1009-086X(2017)-02-0001-05

通信地址：410083 湖南省长沙市岳麓区中南大学航空航天学院 E-mail：xjj@csu.edu.cn

编者按：“2016年先进导航、制导与控制技术研讨会”成功举行。会议得到了国内从事空天防御的军方、军工单位、科研院所、高校等的积极响应和大力支持，共征集到论文40余篇，经过专家评审选出优秀论文10余篇进行了会议交流。《现代防御技术》特开辟专栏陆续刊登此次会议的优秀论文，供读者参考。