基于井间连通性的产聚浓度预测方法
谢晓庆,赵辉,康晓东,张贤松,谢鹏飞(1. 海洋石油高效开发国家重点实验室,北京 100727;2. 中海油研究总院,北京 100727;. 长江大学石油工程学院,武汉40100)
基于井间连通性的产聚浓度预测方法
谢晓庆1, 2,赵辉3,康晓东1, 2,张贤松1, 2,谢鹏飞3
(1. 海洋石油高效开发国家重点实验室,北京 100727;2. 中海油研究总院,北京 100727;3. 长江大学石油工程学院,武汉430100)
为了准确预测产聚时间、产聚浓度等含聚采出液关键指标,提出了基于井间连通性的产聚浓度预测方法,通过与数值模拟软件计算结果的对比进行了验证,并进行了实例分析。在水驱井间连通性模型的基础上,考虑聚合物的黏度、浓度、吸附量和水相渗透率下降系数等关键参数,建立了聚合物驱生产动态预测模型。与传统数值模拟方法相比,该模型需要求解的压力方程组维数较低,且通过自动历史拟合反演井间传导率和连通体积,提高了计算速度和精度。采用1注4采均质油藏模型,通过与数值模拟软件计算结果的对比验证了模型的可靠性和准确性,并对主要模型参数进行了敏感性分析,发现随着注聚后水相渗透率下降系数、注聚浓度和注入孔隙体积倍数的增加以及注聚时机的提前,驱油效果变好。应用实例分析结果表明,建立的模型能有效预测不同开发方案的产聚浓度变化规律。图10参22
井间连通性;产聚浓度;聚合物驱;计算模型
引用:谢晓庆, 赵辉, 康晓东, 等. 基于井间连通性的产聚浓度预测方法[J]. 石油勘探与开发, 2017, 44(2): 263-269, 308.
XIE Xiaoqing, ZHAO Hui, KANG Xiaodong, et al. Prediction method of produced polymer concentration based on interwell connectivity[J]. Petroleum Exploration and Development, 2017, 44(2): 263-269, 308.
0 引言
海上注聚油田由于平台空间有限,采出液处理难度大,采出液中的含聚油泥会影响油田的正常生产。准确预测含聚油泥的产出量是解决该问题的关键,而含聚油泥产出量与产聚浓度息息相关,因此需要准确预测产聚浓度。通过文献调研发现,由于聚合物产出影响因素多,除了沉积微相、储集层非均质性、储集层连通性等地质静态因素,还有注采井距、井网完善程度、注聚速度等开发动态因素[1-4],所以产聚浓度预测难度大、准确性低,目前还没有成熟的预测方法。
常用的聚合物驱开发动态预测方法主要有矿场实验法、数值模拟法、统计学模型法和类比法[5-9]。矿场实验法主要根据区块的产聚情况,结合地质特征分析窜聚规律,具有区域性,难以推广应用。传统数值模拟方法主要通过历史拟合来反演油藏地质模型,再进行生产动态预测得到各井处的聚合物浓度。该方法考虑因素全面,预测功能强大,但历史拟合工作繁冗、计算量大,且由于拟合修正后的地质参数具有极强的不确定性,难以保证预测结果的准确性。统计学模型法计算简单,但模型过于理想化,计算结果可靠性差。由于陆上油田与海上油田的储集层情况和注聚条件差别较大,也不能简单地类比陆上油田产聚规律。
因此,本文基于已经成熟应用于油田的水驱井间连通性模型[10-15],建立聚合物驱产聚浓度预测模型。对模型进行验证,进行主要参数敏感性分析,并进行应用实例研究。
1 模型建立
本文在赵辉等提出的水驱井间连通性模型[10, 14]的基础上,通过考虑聚合物溶液的黏度、浓度、吸附量和水相渗透率下降系数等来建立聚合物驱模型。基于井间连通性思想,将油藏简化为一系列由井间平均传导率Tijk和连通体积Vijk这两个特征参数表征的连通单元,前者表征单元的流动能力,后者反映单元的物质基础。根据地层条件下物质平衡方程,对于第i井:

对(1)式进行隐式差分离散,获得如下压力求解方程组:

通过(2)式求出各井点压力pi之后,可通过井点间压差与平均传导率算得各井点间流量分布。考虑关停井及转注造成井底液流反转等情况,采用(3)式对井点含水率导数进行计算,再利用插值方法反算井点含水饱和度。
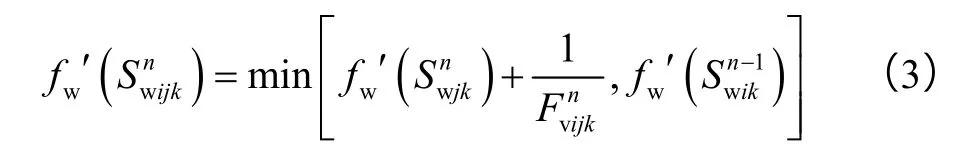
求得井点压力、流量及含水饱和度后,通过浓度的平衡方程求得聚合物浓度分布。聚合物驱涉及油相与含聚合物的水相之间的两相渗流过程,高分子量聚合物的非牛顿流效应和在多孔介质中的吸附/滞留效应影响了相对渗透率。由聚合物驱相对渗透率实验曲线研究[16]可知,相比于水驱,聚合物驱残余油饱和度明显降低,等渗点含水饱和度有所增加,且注聚合物段塞后束缚水饱和度明显增加。
由于井间连通单元内部相对均质,考虑聚合物驱水相特点,以一维线性聚合物驱模型进行聚合物浓度模拟计算。将第i井和第j井间均质连通单元内部划分为m个网格,连通单元内部流量为Qij,且忽略岩石压缩性,孔隙度为φ,网格体积为ΔV。
以第 r网格为对象,聚合物浓度的物质平衡方程为:
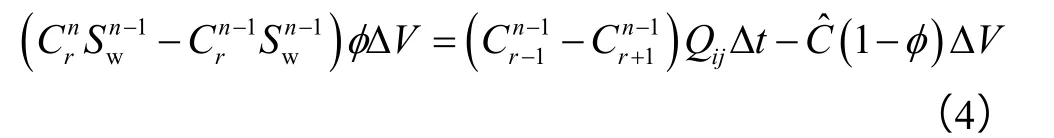
对(4)式进行整理得到聚合物浓度求解表达式:
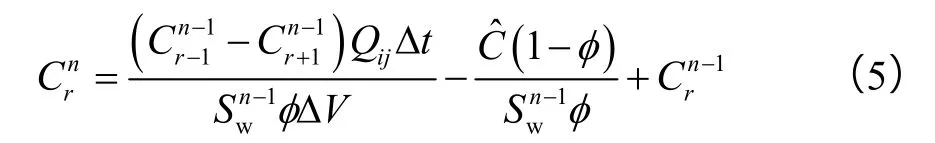
推广到井间连通性模型,以第i井第k层为对象,建立聚合物浓度的物质平衡方程:
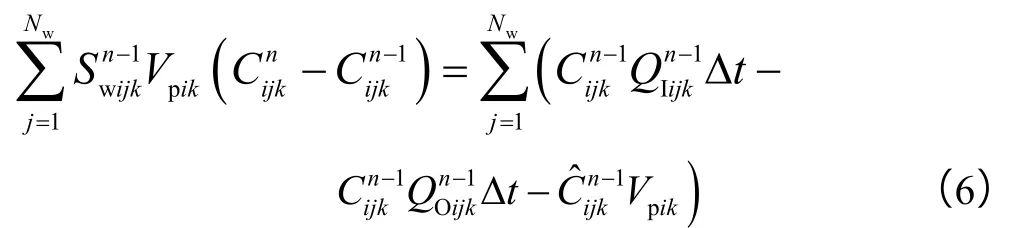
假定聚合物的吸附是瞬间完成的,根据兰格缪尔等温吸附定律,可计算出一定浓度的聚合物在地层中的吸附量[17-20]:
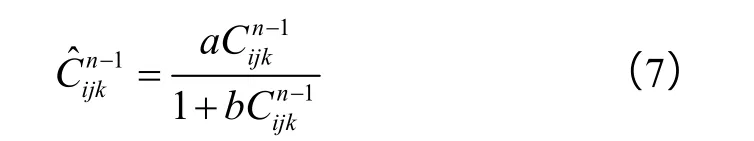
(7)式中 a、b由实验测得。在求出各井点各层的聚合物浓度后,便可求得聚合物溶液的黏度及注聚后水相的渗透率下降系数,进而求得各井点的分流量。

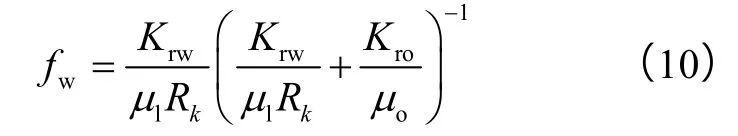
(8)式中α、β、γ的具体数值由实验确定[21]。(9)式中 Rmax为最大渗透率下降系数,其计算较为复杂,可以通过室内实验测定[22]。
相对于传统数值模拟方法,本文建立的聚合物驱模型需要求解的压力方程组维数较低,与井数相等(见(2)式),且含水饱和度追踪是以连通单元为对象、通过半解析方法求解。因此,整体运算量较小,计算快速、稳定,油藏井网越完善,所建模型反映的油水动态与实际情况就越接近。实际计算中,对于注采井网不完善的部分,可人为补充产量为零的虚拟井进行完善。同时,模型计算精确程度取决于井间平均传导率和连通体积这两个参数,因此结合最优化理论,通过对油田生产历史动态的快速拟合,实现模型参数自动反演,提高模型的拟合精度及预测能力,具体过程可参见文献[10]和[15]。本文基于 Windows平台和Fortran语言编制了基于井间连通性的聚合物驱动态预测计算程序。
2 模型验证
借助油藏数值模拟技术对本文建立的模型进行验证,油藏模型为1注4采均质模型。采用Eclipse数值模拟软件进行了生产动态模拟,模拟时间2 500 d,注入量400 m3/d,单井产量100 m3/d,油、水的黏度分别为50 mPa·s和1 mPa·s,在生产410 d单井含水率为92%时开始注聚,注入孔隙体积倍数 0.2,注聚浓度1 000 mg/L,最大渗透率下降系数1.5,α、β、γ分别为1.30、1.05、2.20。运用本文模型对含水率和产聚浓度的数值模拟结果进行了拟合(见图 1、图 2),发现拟合效果良好,相关系数分别达到89.3%和97.0%。注聚后含水率降低,形成“漏斗”(见图1),说明聚合物驱油效果明显。产聚浓度先升高后降低(见图2)。拟合后油井与水井间连通体积和传导率分别为 3.26×104m3和0.94 m3/(d·MPa),油井与油井间连通体积和传导率分别为5.30×104m3和0.71 m3/(d·MPa)。

图1 含水率曲线拟合结果
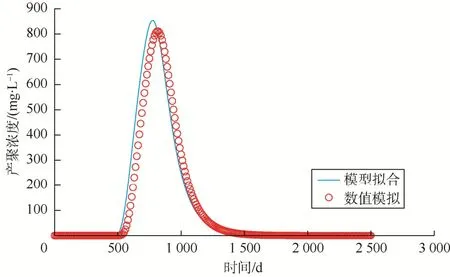
图2 聚合物产出浓度曲线拟合结果
3 模型参数敏感性分析
对模型参数进行敏感性分析,主要研究注聚后水相的渗透率下降系数、注入浓度、注入孔隙体积倍数和注入时机对聚合物驱油效果的影响。在对某一参数进行分析时,只对该参数取不同值,其他参数值均与模型验证时的参数值相同。
3.1 注聚后水相的渗透率下降系数
由于聚合物溶液首先进入高渗透层,造成高渗透层水相渗透率下降,从而扩大了聚合物驱的波及体积。渗透率下降系数越大,见效越早,含水率下降幅度越大、“漏斗”越宽,聚合物驱效果越好。可以通过调整(9)式中Rmax的值来研究渗透率下降系数对聚合物驱油效果的影响规律。采用本文模型计算Rmax分别为1.5、2.0、2.5、3.0和 3.5时的含水率和产聚浓度变化曲线(见图3)。可以看出,注聚后水相的渗透率下降系数越大,含水率下降得越快、“漏斗”越宽,驱油效果越好,而产聚浓度的变化很小。
3.2 注入聚合物浓度
采用本文模型计算注聚浓度分别为1 000、1 200、1 400、1 600和1 800 mg/L时的含水率和产聚浓度变化曲线(见图4)。可以看出,随着注聚浓度的增加,含水率下降幅度增大,原油采收率提高,产聚浓度的峰值显著增大。
3.3 注入孔隙体积倍数
在注聚浓度1 000 mg/L条件下,分别注入0.10、0.15、0.20、0.25和 0.30倍孔隙体积的段塞。由图 5可知,随着注入孔隙体积倍数的增大,含水率下降“漏斗”的宽度变大,产聚浓度的峰值不断增大,且从峰值开始减小的时间后延。
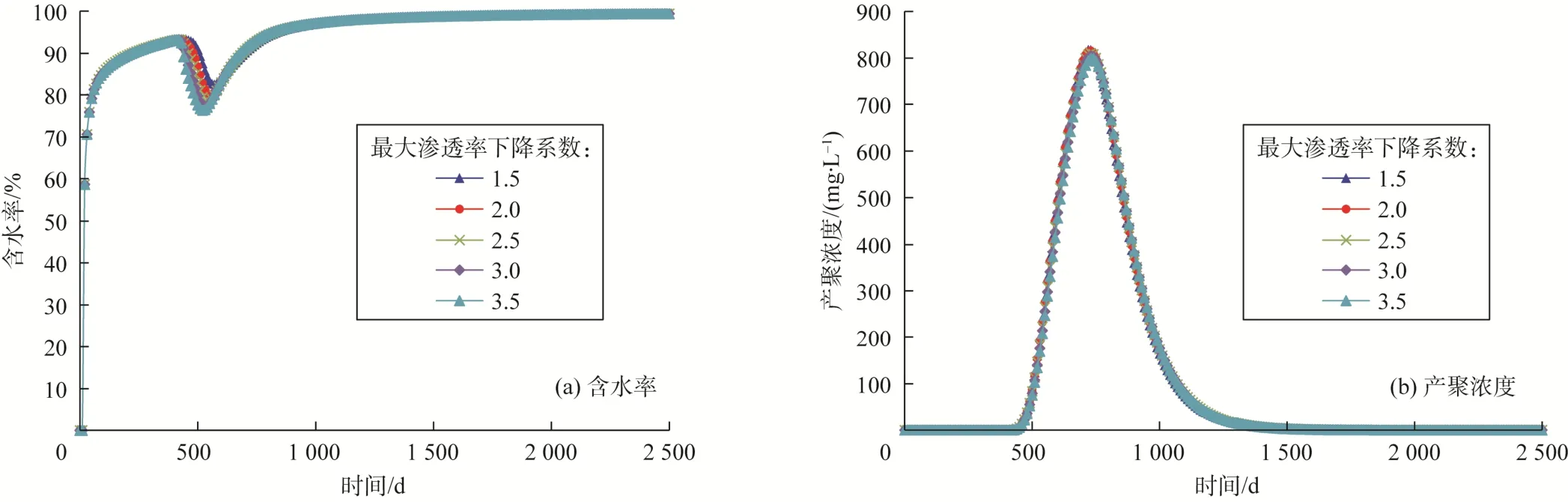
图3 不同渗透率下降系数下的含水率和产聚浓度变化曲线
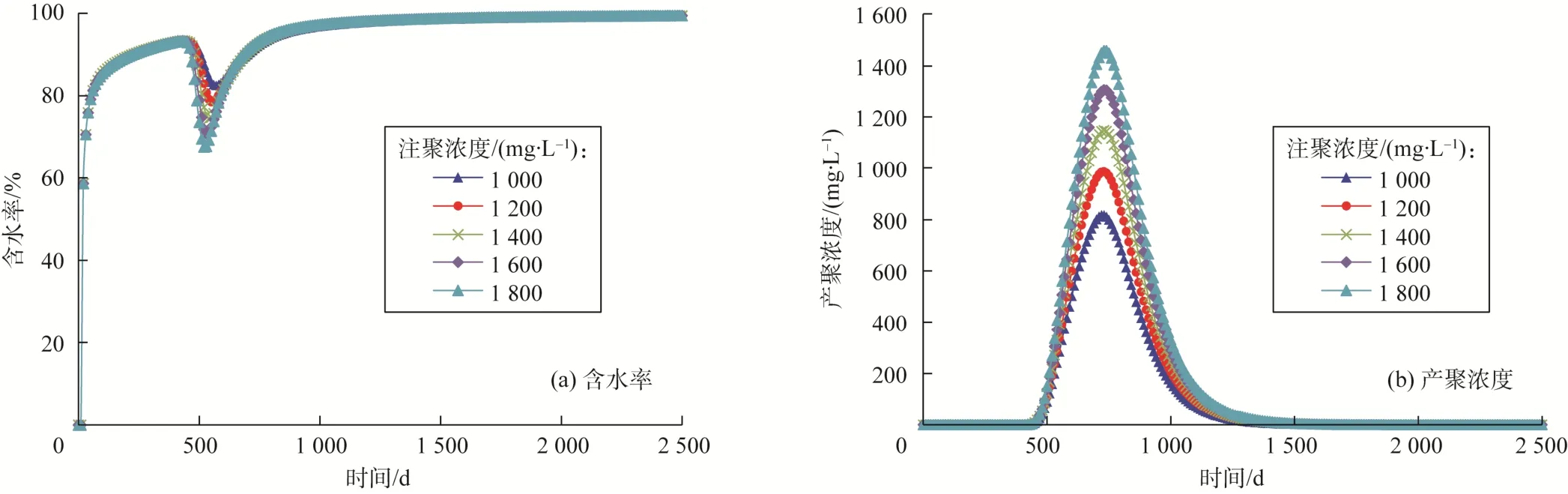
图4 不同注聚浓度下的含水率和产聚浓度变化曲线

图5 不同注入孔隙体积倍数下的含水率和产聚浓度变化曲线
3.4 注入聚合物时机
转聚合物驱的时机越早,驱替效果越好,且能有效地缩短开采时间,节约注水量,提高经济效益。由图 6可知,随着注聚时机的提前,见效、见聚越早,但产聚浓度的峰值变化不大。
4 应用实例
采用编制的程序对实际油田进行模拟计算,通过自动历史拟合,得到连通性模型参数,从而对不同开发方案的产聚浓度进行预测。
4.1 典型区块模型历史拟合
以某海上油田注聚油层组为例,区块连通性模型参数反演结果如图 7所示,该图直观地显示了井间尤其是注聚井与周围井间传导率和连通体积的大小。区块和单井的拟合情况分别如图8和图9所示,可以看出,区块的含水率、累计产油和累计产液等主要参数的拟合相关系数均达到 90%以上,区块和单井的产聚浓度拟合效果较好。
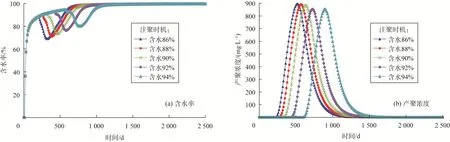
图6 不同注聚时机下的含水率和产聚浓度变化曲线
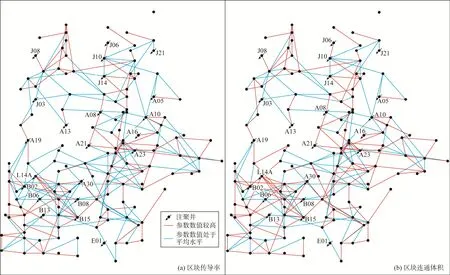
图7 区块传导率及连通体积反演结果
4.2 不同方案产聚浓度预测
由于模型的拟合效果较好,可以用来预测不同开发方案的产聚浓度变化规律。方案1:保持目前注聚井24口不变,注聚到2016年6月30日结束。方案2:保持目前注聚井24口不变,注聚到2019年4月30日结束。方案3:增加注聚井至45口,注聚到2021年12月结束。图10为3个方案的产聚浓度预测曲线,可以看出,产聚浓度先增加后降低,达到一个峰值后快速回落。方案1中注聚停止4个月后产聚浓度达到峰值106 mg/L,方案2中注聚停止5个月后产聚浓度达到峰值152 mg/L,方案 3中注聚停止 5个月后产聚浓度达到峰值 233 mg/L。图10中检测值为现场根据方案1进行生产的实际产聚浓度,与本文方法预测结果具有较好的一致性。
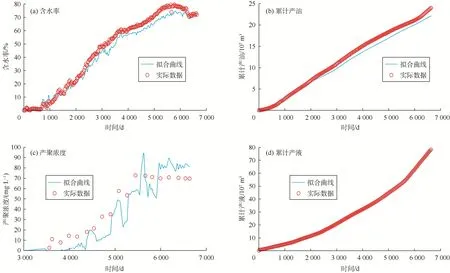
图8 区块拟合情况

图9 单井产聚浓度拟合情况

图10 不同方案的产聚浓度预测结果
5 结论
本文所建立的基于井间连通性的聚合物驱模型,在遵循聚合物驱渗流规律的基础上,能快速计算各项生产动态指标,结合最优化算法,对模型参数进行自动历史拟合,并可对产聚浓度进行快速、准确预测。
通过与数值模拟软件计算结果的对比验证了本文模型的可靠性和准确性。实例分析结果表明,模型拟合效果良好,能有效指导聚合物驱开发方案的制定。
符号注释:
a——吸附能力与b的比值;b——聚合物吸附速度与脱附速度的比值;C——聚合物浓度,kg/m3;Cr——第 r个网格的聚合物浓度,kg/m3;——单位体积固体对聚合物的吸附质量,kg/m3;Cijk——第k层i井与j井间连通单元的聚合物浓度,kg/m3;Ctk——第 k层的综合压缩系数,MPa-1;fw——含水率,f;)——在第k层从第j井追踪到第i井处的含水率导数;)——第j井在第k层的含水率导数;Fvijk——从第j井流向第i井的无因次累计流量;Kro——油相相对渗透率;Krw——水相相对渗透率;Nl——油层数;Nw——注采井数;pi,pj——第i井和第j井泄油区内的平均压力,MPa;qi——第i井流量,注入为正、产出为负,m3/s;Qij——一维线性聚合物驱模型连通单元内部流量,m3/s;QIijk,QOijk——第k层i井与j井间连通单元流入和流出的流量,m3/s;Rk——第 k层注聚后水相的渗透率下降系数;Rmax——最大渗透率下降系数;Swik——第i井在第k层的含水饱和度,f;Sw——含水饱和度,f;Swijk——第k层i井与j井间连通单元的含水饱和度,f;t——时间,s;Δt——时间步长,s;Tijk——第 k层 i井和 j井间的平均传导率,m3/ (s·MPa);Vijk——第 k层 i井与 j井间连通体积,m3;Vpik——第k层第i井的泄油体积,m3;ΔV——一维线性聚合物驱模型网格体积,m3;α,β,γ——方程系数;μl——聚合物溶液黏度,mPa·s;μo——油相黏度,mPa·s;μw——水相黏度,mPa·s;φ——孔隙度,f;ζi,ψi,ωi——中间变量。上标:n——当前时刻,s;n-1——上一时刻,s。下标:i,j——不同井的序号;k——油层序号;r——网格序号。
[1] 胡东, 江厚顺, 杨宁, 等. 孤东油田中二南区 Ng3-5单元聚合物驱油见效见聚规律研究[J]. 江汉石油学院学报, 2003, 5(增刊): 86-87. HU Dong, JIANG Houshun, YANG Ning, et al. Law of polymer breakthrough of polymer displacement in unit Ng3-5of south region in block Zhong’er of Gudong oilfield[J]. Journal of Jianghan Petroleum Institute, 2003, 5(Supp.): 86-87.
[2] 邹玮, 陈玉琨, 楼仁贵, 等. 新疆油田七东1区砾岩油藏聚合物驱见聚特征与影响因素研究[J]. 石油知识, 2015(1): 50-52. ZOU Wei, CHEN Yukun, LOU Rengui, et al. Study on polymer flooding characteristics and influencing factors of conglomerate reservoir in Qidong 1 block of Xinjiang Oilfield[J]. Petroleum Knowledge, 2015(1): 50-52.
[3] 安新明. 萨中油田聚合物驱开发规律研究[D]. 大庆: 大庆石油学院, 2007. AN Xinming. Study on development law of Sazhong oilfield with polymer flooding[D]. Daqing: Daqing Petroleum Institute, 2007.
[4] 陶德硕. 水驱和聚合物驱油藏井间动态连通性定量识别研究[D].青岛: 中国石油大学(华东), 2011. TAO Deshuo. Study on inferring interwell connectivity quantitatively from well signals in waterfloods and polymerfloods[D]. Qingdao: China University of Petroleum (East China), 2011.
[5] 陈福明, 卢金凤, 陈鹏. 聚合物驱开采指标测算方法研究[J]. 大庆石油地质与开发, 1999, 18(2): 33-39. CHEN Fuming, LU Jinfeng, CHEN Peng. Method for calculating production index by polymer flooding[J]. Petroleum Geology & Oilfield Development in Daqing, 1999, 18(2): 33-39.
[6] 赵国忠, 孟曙光, 姜祥成. 聚合物驱含水率的神经网络预测方法[J]. 石油学报, 2004, 25(1): 70-73. ZHAO Guozhong, MENG Shuguang, JIANG Xiangcheng. Neural network method for prediction of water cut in polymer flooding[J]. Acta Petrolei Sinica, 2004, 25(1): 70-73.
[7] 单联涛, 张晓东, 朱桂芳. 基于三层前向神经网络的聚合物驱含水率预测模型[J]. 油气地质与采收率, 2007, 14(5): 56-60. SHAN Liantao, ZHANG Xiaodong, ZHU Guifang. Predicting model of water cut by polymer flooding based on three-layer forward neural network[J]. Petroleum Geology and Recovery Efficiency, 2007, 14(5): 56-60.
[8] 赵辉, 李阳, 曹琳. 聚合物驱含水率变化定量表征模型[J]. 石油勘探与开发, 2010, 37(6): 737-742. ZHAO Hui, LI Yang, CAO Lin. A quantitative mathematic model for polymer flooding water-cut variation[J]. Petroleum Exploration and Development, 2010, 37(6): 737-742.
[9] 刘朝霞, 韩东, 王强. 改进的聚合物驱开发动态预测模型[J]. 油气地质与采收率, 2011, 18(4): 54-58. LIU Zhaoxia, HAN Dong, WANG Qiang. A new forecast model for polymer flooding production performance[J]. Petroleum Geology and Recovery Efficiency, 2011, 18(4): 54-58.
[10] 赵辉, 康志江, 孙海涛, 等. 水驱开发多层油藏井间连通性反演模型[J]. 石油勘探与开发, 2016, 43(1): 99-106. ZHAO Hui, KANG Zhijiang, SUN Haitao, et al. An interwell connectivity inversion model for waterflooded multilayer reservoirs[J]. Petroleum Exploration and Development, 2016, 43(1): 99-106.
[11] 赵辉, 李阳, 高达, 等. 基于系统分析方法的油藏井间动态连通性研究[J]. 石油学报, 2010, 31(4): 633-636. ZHAO Hui, LI Yang, GAO Da, et al. Research on reservoir interwell dynamic connectivity using systematic analysis method[J]. Acta Petrolei Sinica, 2010, 31(4): 633-636.
[12] 赵辉, 姚军, 吕爱民, 等. 利用注采开发数据反演油藏井间动态连通性[J]. 中国石油大学学报(自然科学版), 2010, 34(6): 91-94. ZHAO Hui, YAO Jun, LYU Aimin, et al. Reservoir interwell dynamic connectivity inversion based on injection and production data[J]. Journal of China University of Petroleum (Edition of Natural Science), 2010, 34(6): 91-94.
[13] KANG Zhijiang, ZHAO Hui, ZHANG Hui, et al. Research on applied mechanics with reservoir interwell dynamic connectivity model and inversion method in case of shut-in wells[J]. Applied Mechanics and Materials, 2014, 540: 296-301.
[14] 赵辉, 康志江, 张允, 等. 表征井间地层参数及油水动态的连通性计算方法[J]. 石油学报, 2014, 35(5): 922-927. ZHAO Hui, KANG Zhijiang, ZHANG Yun, et al. An interwell connectivity numerical method for geological parameter characterization and oil-water two-phase dynamic prediction[J]. Acta Petrolei Sinica, 2014, 35(5): 922-927.
[15] ZHAO Hui, LI Gaoming, REYNOLDS A C. Large-scale history matching with quadratic interpolation models[J]. Computational Geosciences, 2013, 17(1): 117-138.
[16] 唐金星, 陈铁龙, 何劲松, 等. 聚合物驱相对渗透率曲线实验研究[J]. 石油学报,1997, 18(1): 83-87. TANG Jinxing, CHEN Tielong, HE Jinsong, et al. An experimental study on relative permeability curves of polymer flooding[J]. Acta Petrolei Sinica, 1997, 18(1): 83-87.
[17] 宋考平, 聂洋, 邵振波, 等. 聚合物驱油藏剩余油饱和度分布预测的φ函数法[J]. 石油学报, 2008, 29(6): 899-902. SONG Kaoping, NIE Yang, SHAO Zhenbo, et al. φ-function method for estimating residual oil saturation distribution in polymer-drive reservoir[J]. Acta Petrolei Sinica, 2008, 29(6): 899-902.
[18] SORBIE K S, PARKER A, CLIFFORD P J. Experimental and theoretical study of polymer flow in porous media[R]. SPE 14231, 1987.
[19] 徐建平, 王连泽, 朱克勤. 聚合物驱油藏浓度分布与变化[J]. 清华大学学报(自然科学版), 2002, 42(4): 455-457. XU Jianping, WANG Lianze, ZHU Keqin. Concentration distribution and variation in a polymer-flooding reservoir[J]. Journal of Tinghua Univ. (Sci. & Tech.), 2002, 42(4): 455-457.
[20] 朱怀江, 罗健辉, 隋新光, 等. 新型聚合物溶液的微观结构研究[J]. 石油学报, 2006, 27(6): 79-83. ZHU Huaijiang, LUO Jianhui, SUI Xinguang, et al. Microstructure of novel polymer solution used for oil displacement[J]. Acta Petrolei Sinica, 2006, 27(6): 79-83.
[21] HAN D K, YANG C Z, ZHANG Z Q, et al. Recent development of enhanced oil recovery in China[J]. Journal of Petroleum Science and Engineering, 1999, 22(1/2/3): 181-188.
[22] ZAITOUN A, KOHLER N. Two-phase flow through porous media: Effect of an adsorbed polymer layer[R]. SPE 18085, 1988.
(编辑 胡苇玮)
Prediction method of produced polymer concentration based on interwell connectivity
XIE Xiaoqing1, 2, ZHAO Hui3, KANG Xiaodong1, 2, ZHANG Xiansong1, 2, XIE Pengfei3
(1. State Key Laboratory of Offshore Oil Exploitation, Beijing 100727, China; 2. CNOOC Research Institute, Beijing 100727, China; 3. College of Petroleum Engineering, Yangtze University, Wuhan 430100, China)
To forecast some key parameters of produced liquid containing polymer, including the time of polymer output, polymer concentration, a polymer concentration prediction method based on interwell connectivity methodology was established, its prediction results were compared with those from numerical simulation software, and it has been used in a case study. On the basis of water flooding interwell connectivity model, a polymer flooding production performance prediction model considering the viscosity, concentration, adsorption and water-phase permeability reduction factor of polymer was built. Compared with the traditional numerical simulation, the pressure equations in this model have lower dimension, and it inverses the interwell conductivity and connected volume through automatic history matching, enhancing calculation speed and precision significantly. The calculation model was used to the history matching of a homogeous reservoir model with 1 injector and 4 producers, and the comparison of its results and the results from numerical simulation software shows the model is reliable and accurate. Moreover, sensitivity analysis of major model parameters reveals that the increase of water-phase permeability reduction factor, injected polymer concentration and pore volume injected and early polymer injection time can improve oil recovery. The real reservoir application shows the model can predict the change of produced polymer concentration of different development schemes accurately.
interwell connectivity; produced polymer concentration; polymer flooding; calculation model
国家科技重大专项“海上稠油化学驱油技术”(2016ZX05025-003);海洋石油高效开发国家重点实验室第三批开放基金“海上油田聚合物驱窜聚动态识别与优化控制研究”(2015-YXKJ-001)
TE319
A
1000-0747(2017)02-0263-07
10.11698/PED.2017.02.11
谢晓庆(1982-),男,河南南阳人,博士,中海油研究总院高级工程师,主要从事油气田开发工程和提高采收率技术方面的研究。地址:北京市朝阳区太阳宫南街6号院海油大厦B座710室,邮政编码:100028。E-mail:xiexq@cnooc.com.cn
联系作者:赵辉(1984-),男,山东乐陵人,博士,长江大学石油工程学院副教授,主要从事油气田开发、油藏工程及优化控制工程方面的研究。地址:湖北省武汉市蔡甸区大学路一号,长江大学石油工程学院,邮政编码:430100。E-mail: zhaohui-712@163.com
2016-08-15
2017-01-16

