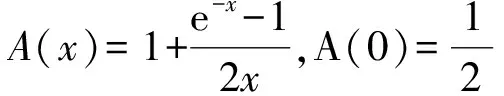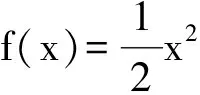一类常微分方程和Volterra积分方程解的存在唯一性
吴 雪 蓉
(南京财经大学 应用数学学院, 江苏 南京 210023)
一类常微分方程和Volterra积分方程解的存在唯一性
吴 雪 蓉
(南京财经大学 应用数学学院, 江苏 南京 210023)
利用Banach压缩映射原理,研究了一类四阶常微分方程和Volterra积分方程解的存在性和唯一性,并且利用MATLAB讨论了此类方程的数值解.
Banach压缩映射原理; 常微分方程; 积分方程; 数值解
在代数方程、微分方程、积分方程、泛函方程等诸多方程问题的研究中,常常会建立与之相关的积分算子T[1-2],把所考虑的方程问题转化为求T的不动点u,即
u=Tu,
不动点理论是泛函分析的主要组成部分,并且有着广泛的应用价值.本文利用Banach压缩映射原理,研究一类常微分方程和Volterra积分方程解的存在性和唯一性.以下我们给出相应的概念定理以及所讨论的方程.
引理1[3](Banach压缩映射原理).设X是完备的度量空间,d是X中的距离,设映射S:X→X满足
d(Sv1,Sv2)≤kd(v1,v2),∀v1,v2∈X,
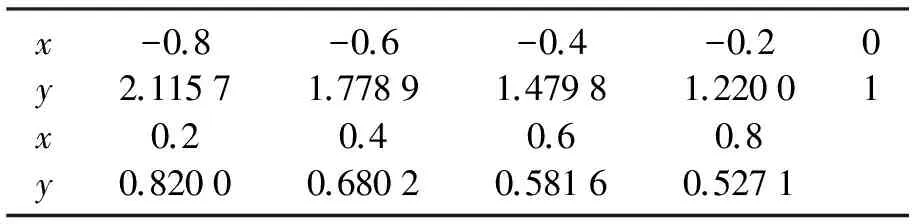
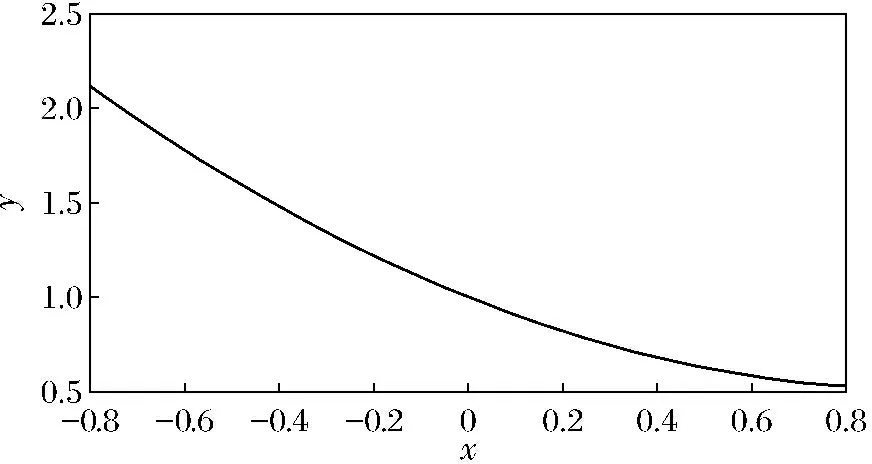
其中 0 讨论下述四阶常微分方程初值问题 (1) 解的存在唯一性. 本文除了研究Banach压缩映射原理在一类常微分方程问题中的应用,还将其应用在第二类Volterra积分方程问题中,积分方程如下: (2) 并且此积分方程的核为 在方程(1)中,总假定: (ⅰ) P(x)在[-r,r]上连续; 于是,得到如下主要结果: 定理1 假设条件(ⅰ)、(ⅱ)成立,则微分方程(1)存在唯一的解. 证明 令F(x)=(y,y′,y″,y(3)), 则F′(x)=(y′,y″,y(3),y(4)).设Φ(x,y0,y1,y2,y3)=(y1,y2,y3,y4)=(y1,y2,y3,Q(x)-P(x)y3),且Γ=(1,-1,1,0),那么方程(1)可转化成如下一阶微分方程: 作积分算子 使得 注意到,如果T存在唯一的不动点,那么方程(1)存在唯一的解,因此,若∀F,G∈C([-r,r],R4), 得到 同理可得 同理可得 因此, 由于 由此可得 故依据Banach压缩映射原理,算子T是一个压缩映射,具有唯一的不动点,因此,微分方程(1)存在唯一的解,定理1得证. 对于积分方程(2),同样可以应用Banach压缩映射原理得到解的存在唯一性,主要结果如下: 定理2 考虑方程(2),则积分方程(2)存在唯一的解. 证明 由于 当0≤t 则M′(y)=-ye-y<0,因此,M(y)在(0,1)上为单调减函数,故M(y) 作积分算子 使得 若对∀φ(x),ψ(x)∈C[-1,1],有 ψ(t)‖∞, 虽然求解微积分方程有各式各样的解析方法,但解析方法只能用来求解一些特殊类型的方程,一般情况下,从一些实际问题中归结出来的方程,都难以求得解析解,此时可以利用MATLAB求其数值解.本节给出了求解上述四阶常微分方程初值问题以及积分方程的数值解法. 例1 对于微分方程(1),取P(x)=x2,Q(x)=2xex,则方程为 (3) 则条件(ⅰ)、条件(ⅱ)成立,依据定理1可知,方程(3)存在唯一的解. 关于高阶微分方程的初值问题,原则上总可以归结为一阶方程组来求解,引进新的变量: 则方程(3)即可化为如下一阶方程组: 满足初值条件y1(0)=1,y2(0)=-1,y3(0)=1,y4(0)=0. 数值结果如表1.图1为方程的近似解的图像. 表1 方程(3)的近似解 图1 方程(3)的近似解图像 Fig.1 The image of approximate solution of equation (3) 例2 用数值积分法[4]来近似求解积分方程 (4) 0≤t≤x≤1, 解 当0≤x 令x=xj(j=1,…,6),得到: 对上式中的定积分用有限和来代替,可得: (5) 式中φj=φ(xj),kjm=k(xj,xm),fj=f(xj). 令 则式(5)可写成Y=KY+F,即(I-K)Y=F,这是一个系数矩阵是下三角的矩阵的线性方程组[5],求解非常方便.下面利用MATLAB编程得到数值结果如表2. 表2 各节点对应的近似解 [1] 郭海杰. 非线性Dirichlet型三点边值问题正解的存在性[J]. 沈阳大学学报(自然科学版), 2016,28(4):340-344. (GUO H J. Existence of positive solutions for nonlinear dirichlet type three point boundary value problems[J]. Journal of Shenyang University(Natural Science), 2016,28(4):340-344.) [2] 马亮亮. 变系数空间分数阶对流扩散方程的有限差分解法[J]. 沈阳大学学报(自然科学版), 2013,25(4):341-344. (MA L L. Finite difference method for fractional convection diffusion equation with variable coefficients[J]. Journal of Shenyang University(Natural Science), 2013,25(4):341-344.) [3] 布莱基斯. 泛函分析:理论和应用[M]. 叶东,周风,译. 北京:清华大学出版社, 2009. (Haim Brezis. Analy fonctionnelle-theorie at applications[M]. YE D,ZHOU F, Translate. Beijing: Tsinghua University Press, 2009.) [4] 沈以淡. 积分方程[M]. 3版. 北京:清华大学出版社, 2012. (SHENG Y D. Integral equations[M]. The third edition. Beijing: Tsinghua University Press, 2012.) [5] 李庆扬,王能超,易大义. 数值分析[M]. 5版. 北京:清华大学出版社, 2015. (LING Q Y, WANG N C, YI D Y. Numerical analysis[M]. The fifth edition. Beijing: Tsinghua University Press, 2015.) 【责任编辑: 肖景魁】 Existence and Uniqueness of Solutions for Ordinary Differential Equations and Volterra Integral Equations WuXuerong (School of Applied Mathematics, Nanjing University of Finance and Economics, Nanjing 210023, China) The existence and uniqueness of solutions for the fourth-orderordinary differential equation and the Volterra integral equation are studied, by using Banach contracting mapping principle. The numerical solutions of these equations are discussed by MATLAB. Banach contracting mapping principle; ordinary differential equation; integral equation; numerical solutions 2016-11-24 吴雪蓉(1992-),女,江苏如皋人,南京财经大学硕士研究生. 2095-5456(2017)02-0168-05 O 175 A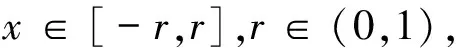
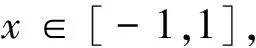
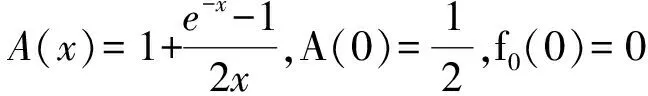
1 解的存在唯一性证明
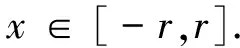
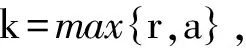
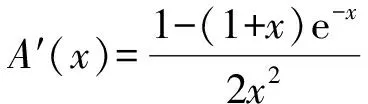
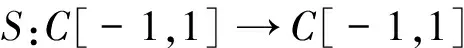
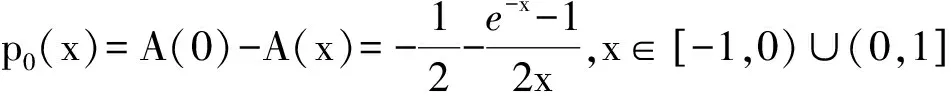
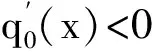
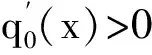
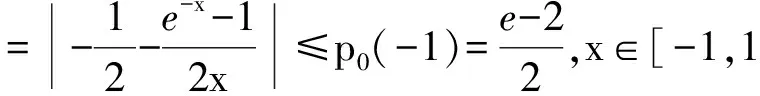
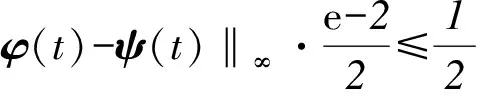
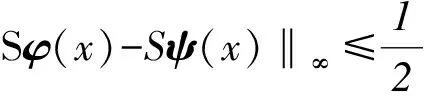
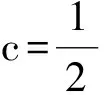
2 具体微分方程和积分方程的数值解