关于M矩阵最小特征值界的不等式

李 艳 艳

(文山学院 数学学院, 云南 文山 663000)



李 艳 艳

(文山学院 数学学院, 云南 文山 663000)

利用变形的Gersgorin圆盘定理和Brauer卵形定理,结合严格对角占优M-矩阵逆矩阵元素新的上、下界估计式,给出了M-矩阵最小特征值的两个新估计式.数值算例说明,新的估计式提高了现有的结果.

M-矩阵;最小特征值;界;圆盘定理

M-矩阵最小特征值的估计是矩阵分析领域中非常重要的研究课题,因为M-矩阵的最小特征值在M-矩阵理论中有着重要应用,例如考察微分方程系统dx/dt=-Ax(t),x(0)=x0>0的解x(t)的l1范数的界问题,其中A是弱链对角占优M-矩阵.

1 相关引理及定义

关于M-矩阵最小特征值的界估计文献[1-8]给出了许多结果.

Shivakumar etal在文献[1]中给出,当A为弱链对角占优M-矩阵时的A的最小特征值(τ(A))的界.

引理1[1]设A=(aij)∈Rn×n是弱链对角占优M-矩阵,A-1=(αij),则

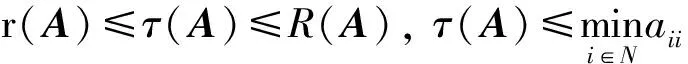
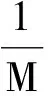
黄廷祝等2010年在文献[2]中,利用非奇异M-矩阵A的迭代矩阵JA给出了τ(A)的新界.

引理2[2]设A=(aij)∈Rn×n是非奇异M-矩阵,A-1=(αij),则

李朝迁,李耀堂2013年在文献[3]中提出了引理2,给出了下面的新结果.

引理3[3]设A=(aij)∈Rn×n是非奇异M-矩阵,A-1=(αij),则

本文继续对该类问题进行研究,给出严格对角占优M-矩阵的最小特征值只与矩阵元素有关的一些新估计式.

下面先给出相关定义

定义1 矩阵A=(aij)∈Rn×n,A≥0表示元素全为非负的 (正)矩阵,称A为非负矩阵(正矩阵).

定义2 记Zn×n={A=(aij)∈Rn×n:aij≤0,i≠j,i,j∈N},若A∈Zn×n,则称A为Z矩阵,简记为A∈Zn×n.如果A=(aij)∈Zn×n是非奇异的,且A-1≥0,则称A为非奇异M-矩阵.

定义3 设矩阵A=(aij),B=(bij)∈Rn×n,用A∘B=(aijbij)表示A和B的对应元素相乘而成的n×n矩阵,称其为A和B的Hadamard积.

引入一些记号

引理4[4]设A=(aij)∈Rn×n,若A是行严格对角占优M-矩阵,则A-1=(αij)满足

引理5[5]若A=(aij)∈Cn×n,x1,x2,…,xn是正实数,则A的所有特征值位于下列区域

引理6[5]若A=(aij)∈Cn×n,x1,x2,…,xn是正实数,则A的所有特征值位于下列区域

2 主要结果

这部分首先给出严格对角占优M-矩阵A的逆矩阵主对角元素的新界,其次给出A的最小特征值的新估计式.

定理1 设A=(aij)∈Rn×n,若A是行严格对角占优M-矩阵,则A-1=(αij)满足

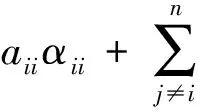
即

同理可证左边成立.

定理2 设A=(aij)∈Rn×n是非奇异的严格对角占优M-矩阵,A-1=(αij),B=(bij)∈Rn×n是非负矩阵,则

证明 因为A是非奇异严格对角占优M-矩阵,则A-1存在且A-1≥0,又因为B是非负矩阵,则A-1∘B是非负矩阵.

(1) 假设A,B是不可约矩阵,则A-1∘B也不可约.

应用引理4,引理5得

则

(2) 当A,B是可约矩阵时,证法与文献[3]类似.

定理3 设A=(aij)∈Rn×n是非奇异的严格对角占优M-矩阵,A-1=(αij),则

证明 当定理2中的B=J(矩阵J的每个元素都是1),得

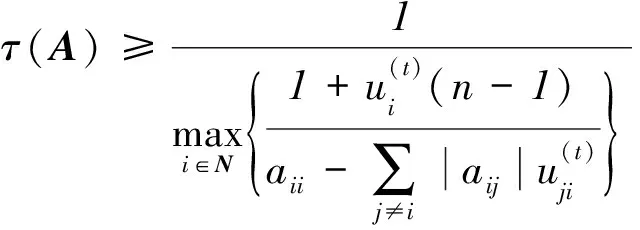
定理4 设A=(aij)∈Rn×n是非奇异的严格对角占优M-矩阵,A-1=(αij),B=(bij)∈Rn×n是非负矩阵,则

ρ(A-1∘B)≤

证明 (1)假设A,B是不可约矩阵,则A-1∘B也不可约.

应用引理4,引理6得

对上述不等式整理得

(2) 当A,B是可约矩阵时,证法与文献[3]类似.

定理5 设A=(aij)∈Rn×n是非奇异的严格对角占优M-矩阵,A-1=(αij),则

证明 类似定理3的证明.

注释:本文所得到的这两个估计式,只与矩阵A的元素有关,计算起来比较方便.

3 数值算例

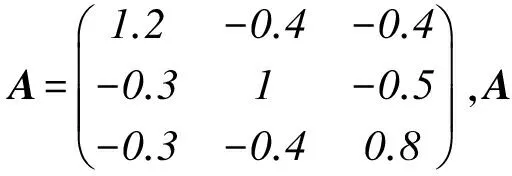
通过该例可以发现,文中所得的估计式提高了文献[3]中的相应结果.

[1] SHIVAKUMAR P N, WILLIAMS J J, YE Q, et al. On two-sided bounds related to weakly diagonally dominant M-matriceswithapplicationtodigitalcircuitdynamics[J].SIAMJournalonMatrixAnalysisandApplications, 1996,17(2):298-312.

[2] TIAN G X, HUANG T Z. Inequalities for the minimum eigenvalue ofM-matrices[J]. Electronic Journal of Linear Algebra, 2010,20(1):291-302.

[3] LI C, LI Y, ZHAO R. New inequalities for the minimum eigenvalue ofM-matrices[J]. Linear and Multilinear Algebra, 2013,61(9):1267-1279.

[4] 赵建兴.M-矩阵最小特征值估计及其相关问题研究[D]. 昆明:云南大学, 2014:8-14. (ZHAO J X. Estimation of minimum eigenvalue ofM-matrix and its related researches[D]. Kunming: Yunnan University, 2014:8-14.)

[5] 陈景良,陈向晖. 特殊矩阵[M]. 北京:清华大学出版社, 2000. (CHEN J L, CHEN X H. Topics matrix[M]. Beijing: Beijing University Press, 2000.)

[6] HORN R A, JOHNSON C R. Topics in matrix analysis[M]. Cambridge: Cambridge University Press, 1995.

[7] 李艳艳,王东政. 严格对角占优M-矩阵最小特征值的新界[J]. 沈阳大学学报(自然科学版), 2015,27(3):255-258. (LI Y Y, WANG D Z. New bounds of minimum eigenvalue of strictly diagonally dominantM-matrix[J]. Journal of Shenyang University(Natural Science), 2015,27(3):255-258.)

[8] 王跃华,王洁英. 关于不等式几种常见证明方法的探究[J]. 沈阳大学学报(自然科学版), 2013,25(5):428-430). (WANG Y H, WANG J Y. Several common methods of proof of inequality[J]. Journal of Shenyang University(Natural Science), 2013,25(5):428-430.)

【责任编辑: 肖景魁】

Inequality on Minimum Eigenvalue Bounds ofM-Matrix

LiYanyan

(School of Mathematics, Wenshan University, Wenshan 663000, China)

Using the deformed Gersgorin disk theorem and the Brauer oval theorem, combining with new upper and lower bounds for the inverse matrix elements of strictly diagonally dominantM-matrices, two new estimators for the minimum eigenvalue ofM-matrix are given. Numerical examples illustrate that the new estimator improves the existing results.

M-matrix; minimum eigenvalue; bound; disk theorem

2016-09-07

云南省科技厅应用基础研究项目(2013FD052); 文山学院科学研究项目(16WSY11).

李艳艳(1982-),女,甘肃庆阳人,文山学院讲师.

2095-5456(2017)02-0164-04

O 151.21

A