负载下轴压加固柱受力性能试验
周 乐, 聂晓梅, 王克尧, 郑 媛
(沈阳大学 建筑工程学院, 辽宁 沈阳 110044)
负载下轴压加固柱受力性能试验
周 乐, 聂晓梅, 王克尧, 郑 媛
(沈阳大学 建筑工程学院, 辽宁 沈阳 110044)
为了进一步研究负载下外包钢筋混凝土法加固钢柱的轴压力学性能,进行了7根加固柱和1根纯钢柱的轴压静载试验.试验主要考虑初始负载大小、混凝土强度及箍筋直径三个参数对构件受力性能的影响.由试验得出加固柱在轴心载荷下的破坏形态、载荷-位移曲线及载荷-应变曲线,分析了加固柱的破坏机理和三个变化参数对其轴压性能的影响,提出了加固柱轴压承载力计算公式.结果表明,加固柱的承载力随配箍率和混凝土强度的提高而明显增加;初始负载越大,钢筋混凝土应变滞后现象越严重,加固柱承载力越低.加固柱轴压承载力的计算时对新增部分材料的强度应进行一定的折减.
加固柱; 轴压性能; 应变滞后; 极限承载力
为改善在役钢结构建筑易腐蚀、防火性能差和易发生局部屈曲等问题,目前工程中主要采用栓焊接并用、外包钢、外包碳纤维、预应力等加固方式对钢结构进行加固.但由于施工条件的限制,这些加固方法存在施工难度大、 适用范围窄、造价偏高等问题,急需新的加固方式来弥补这些加固方法的不足.
文献[1-2]中指出型钢混凝土结构具有承载力高、抗震性能好、应用广泛、施工方便等优点.李惠等[3]通过对5根钢-混组合柱进行了低周往复载荷作用下的轴压试验,首次提出型钢负载下四周包裹钢筋混凝土的设想,分析了型钢的预压,提高组合柱的抗震性能.在此之后,吴波等[4]通过非线性分析法对截面弯矩-曲率进行分析,建立了三折线模型表示此种构件柱截面弯矩-曲率的关系,并确定了相应模型参数.继这以后,长沙理工大学[5-6]在低周往复加载方式下对型钢先负载再外围混凝土的结构,用ANASYS软件进行了大量的模拟,得到负载钢-混组合柱在不同轴压比、型钢负载比下的破坏形态,并分析了轴压比、负载比对构件抗震性能的影响,得出了此构件最适轴压比、负载比的计算公式.
为分析负载下外包钢筋混凝土加固后轴压加固柱的受力机理,研究初始负载混凝土强度及箍筋直径对加固柱承载力的影响,为加固柱轴心受压时承载力设计方法提供参考,本文进行了7根加固柱和1根纯钢柱的轴压一次性破坏试验,并结合有限元模拟和简单叠加法理论推导,提出适合此种钢结构加固法的承载力计算公式.
1 试验概况
1.1 构件设计与制作
试验中设计并制作7根SRHC柱构件和1根纯钢柱对比构件.核心型钢均采用热轧Q235级工字钢,柱高1.2 m.加固柱、纵筋均配置HRB335级钢筋,配置为4φ14,箍筋采用HPB235级钢筋,配置依次为φ6.5@100、φ8@100、φ10@100,混凝土采用C40、C60、C80三种强度等级,加固后构件的截面尺寸均为200 mm×200 mm,构件配筋情况及截面尺寸详见图1,主要参数见表1.参照 GB/T 228—2002 《金属材料室温拉伸试验方法》及文献[7],测得钢材的力学性能如表2所示,表中,L为加固柱截面长度,H为加固柱截面高度,Nl、Nu分别是负载下外包钢筋混凝土加固时钢柱的初始载荷和屈服载荷.

表1 试验设计参数

图1 构件截面尺寸及配筋

钢材类型E/GPaνσS/MPaσb/MPa工字型钢2060.25295.68370ϕ14钢筋2000.3385.32510ϕ6.5箍筋2100.3235375钢垫板2060.25235370
1.2 试验装置及量测方案
试验设备主要分为加载和数据采集设备两个部分.加载设备为沈阳建筑大学结构工程试验室所提供的5 000 kN液压千斤顶和横梁立柱及JSF高精度静态伺服液压控制台组成的加载系统,数据采集设备为鞍山东信测试353993D静态数据采集箱,加载装置及测点布置见图2.
此次试验中构件为二次受力,采用两阶段加载方案[8].第一阶段,对型钢进行加载,施加竖向载荷直至达到设定值后进行钢筋绑扎,再浇注混凝土使之成型.第二阶段,使用可承受5 000 kN的试验机进行实验,将所制作满足要求混凝土加固柱平稳放置在实验设备上,采用匀速分级进行加载[9]:第一步为预加载,对构件进行三次预加载,且每次的预加载值都为1/20Nu,卸载时分两次进行.第二步为正式加载.预加载卸载完成后,间隔10 min,对构件进行正式加载,且加载以破坏载荷的1/10作为增量开始递增,当构件开始出现开裂或即将开裂时,将加载增量由破坏载荷的1/10改为1/20Nu,并继续增加载荷直到构件破坏.

图2 加载装置及测点布置
试验过程中,在构件顶部安装力传感器,测量构件的轴向载荷.试验中针对构件位移的测量采用YDH-100型位移计测量,为了测量构件变形量,在构件两端部、距离上下端部的两1/4截面和中部布置水平位移计,测量其横向变形,在构件的上下两个端部布置两个竖向位移计,以测定构件各试验阶段的竖直变形,对于构件整体竖向位移的测量由压力机竖向位移作为校核,测点布置见图2.
试验中,对于钢结构构件、受力钢筋及混凝土表面相应位置上应变的测量,其中沿工字钢长度1/4、1/2、3/4处的上下翼缘和腹板分别粘贴3个纵向应变片和1个横向应变片;沿构件高度范围内的受力钢筋中部及1/4截面处各布置1个应变片;混凝土邻对侧3个面上,相应于型钢的位置的中部、距离上下端部的两1/4截面的上下400 mm范围内布置应变片,图2为测点示意图.有关数据通过电液伺服试验机和静态数据采集仪自动采集,包括受力,位移和应变情况.
2 主要试验结果及分析
2.1 构件破坏状态
各构件的破坏形态如图3所示,在第一次施加预定大小的轴向载荷时,型钢一直处于弹性阶段.第二次加载初期,加固柱处于弹性阶段,型钢、钢筋和混凝土三者协调工作,变形基本一致,构件变化形态一致.当加载至各构件0.5Nu时,细小裂痕开始在构件上出现,且位于构件中部,持续加载至0.7Nu时,纵向裂缝延伸至构件中部,并伴有响声,此时混凝土及纵筋应变急剧增加,构件中部出现大量纵向裂缝.当载荷达到0.95Nu左右时,裂缝急剧增加,响声连连.继续加载,构件中部混凝土出现脱落情况,对构件强度产生较大影响,随后构件两端发生破坏.持续对构件加载,其承载力逐渐减小,承载力下降至峰值载荷的85%时停止加载[10].
与普通型钢混凝土柱相比,加固柱开始出现较为明显的粘结力下降情况,具体表现为出现滑移.此时裂缝竖向分布于型钢翼缘,特别是在其发生屈服现象后,继续加载不久构件就被破坏.SRHC-6、SRHC-7两构件开裂时间相对晚些,混凝土表面出现大量裂缝后,构件破坏过程相对迟缓,说明箍筋对箍筋以内混凝土及型钢有重要约束作用,箍筋直径的增大提高了发生粘结滑移后的型钢与混凝土结合面的机械咬合力和摩擦阻力.构件SRHC-3经过较短时间、受到较小载荷增量后便发生了破坏,表明第一次受力时,型钢已经承受较大载荷,第二次加载时,型钢承受形变能力有限,从加载到破坏,型钢作用比较明显.实验结束后,将混凝土剖开后观察,混凝土被压碎处型钢出现少许弯曲、钢筋压弯突出,而型钢翼缘内混凝土仍与型钢紧密接触,没有压碎现象.
构件S-8在加载至0.7Nu左右时,型钢翼缘开始屈曲,继续加载至0.8Nu左右时,型钢腹板开始出现屈曲,加载至Nu左右型钢柱最终破坏时,呈现出明显的S型弯曲,继续加载,构件变形继续加大.当载荷下降到0.9Nu左右时,试件彻底失去承载能力.

图3 构件破坏形态
试验所得构件的载荷-位移曲线见图4.试验中做参照的对比件与加固柱有着较为相似的变化趋势,载荷达到极限载荷之前为线性变化,当达到载荷极限后,承载力渐渐降低,构件位移持续增加.与对比构件S-8相比,加固柱承载力均有显著提高,且随初始负载的增大而减小,随混凝土强度和箍筋直径的提高而减小.混凝土强度为68.96 MPa时,构件SRHC-1承载力较对比构件S-8提高1 940 kN;初始负载为0.3Nu时,SRC-4(40.5 MPa)、SRHC-5(80 MPa)、SRHC-6(d=8 mm)、SRHC-7(d=10 mm)分别较构件SRHC-2承载力提高-22.3%、14.7%、7.68%、20.7%;其他条件(如混凝土强度和配箍率)都相同时,构件SRHC-2、SRHC-3较构件SRHC-1对应承载力分别下降11.38%、22.48%.
普通型钢柱在载荷加载至0.9Nu左右前,载荷-位移曲线仍大致呈线性关系[11],本试验加固柱是加固至0.75Nu左右前,其载荷-位移曲线仍大致保持线性关系.构件SRHC-2的位移比构件SRHC-1增大24.48%,构件SRHC-3的轴向位移比构件SRHC-1增大63.4 %,说明构件轴向位移随初始负载的增加而增大,这主要是因为初始负载越大,试验过程中型钢屈服的越早,刚度降低越快,再加上实际工程中柱的端部受力要大于柱的中部,初始负载大的柱中,同一时刻钢筋混凝土承受的轴力比其他柱要大,因为型钢具有延性,在其屈服后的一定时间里仍可以发生一定形变,导致最后破坏时的位移增大; 构件SRHC-4的轴向位移比构件SRHC-2提高20.04%,构件SRHC-5的轴向位移比构件SRHC-2减小23.03%,说明构件轴向位移随混凝土强度的提高而减小,主要是因为同一条件下,混凝土强度越高的构件刚度越大,本试验构件是在负载下进行的,钢筋混凝土会存在应力滞后现象,型钢最先屈服时新增钢筋混凝土还没有得到充分利用,故最后构件破坏时混凝土强度越大的构件,其最终轴向位移越小.已有研究表明,型钢与混凝土之间的粘结度较钢筋与混凝土要小很多,因此负载下钢结构加固时需配置一定的钢筋来保证型钢与混凝土协同工作.由图5可知,配箍直径最大的构件SRHC-7破坏时轴向位移较配箍直径最小构件SRHC-2减小了9.93%,说明配箍直径的增大对构件变形能力没有明显的改善. 由此可以推断实际工程中进行钢结构加固时, 若原型钢负载已经较大, 则应该尽量卸载, 且混凝土强度和箍筋直径应该适当选取, 以免造价过高却达不到预期效果.
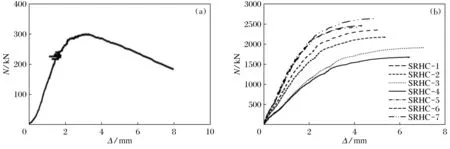
图4 轴向载荷位移曲线
2.3 应变量测
2.3.1 载荷-应变相关曲线
根据图5中载荷-应变曲线可知,加固柱的应变应该分为两个阶段,与原未加固柱相比较,钢筋混凝土承担了一部分载荷,型钢表面的应力分布情况也发生了改变,所受载荷的增量逐渐减小,应变也随之减小.若继续加载,应变曲线回归原趋势,即二次受力构件中存在应力重分布现象.对于不同负载大小的构件,构件破坏时,纵筋、混凝土的破坏应变值随着初始负载的加大而逐渐减小,说明外围钢筋混凝土加固效果随着初始负载的加大而在减小,也说明负载百分比越大,应变超前或者应力滞后现象越严重.对比不同加固混凝土强度等级的应变值可知,初始负载相同时,随着混凝土强度等级的增加,混凝土极限压应变逐渐减小,延性增大;对比不同箍筋直径的构件应变值可知,随着配箍直径的增大,极限压应变逐渐增大.由此可见,适当提高配箍直径可以增大混凝土的延性.

图5 载荷应变曲线
2.3.2 纵筋应变
构件破坏截面处的轴向载荷-纵筋应变曲线如图6所示.构件SRHC-2、SRHC-6、SRHC-7纵筋在所承受的载荷达到极限破坏载荷的0.8~0.85时达到屈服;构件SRHC-2、SRHC-6纵筋在所承受的载荷达到峰值载荷的0.73左右时进入屈服状态;构件SRHC-3破坏截面处的纵向钢筋在所承受的载荷达到峰值载荷的0.93左右时进入屈服状态;构件SRHC-5到破坏时纵筋仍未屈服.由各构件达到极限载荷时的纵筋应变可知,随着初始负载的增大,构件破坏时纵筋的应变越小,纵筋达到屈服时越接近构件破坏时间.构件SRHC-3相较于构件SRHC-1破坏时纵筋应变减小27%,说明初始负载越大,构件达到破坏时新增部分材料利用率越低,从而使构件的最终承载力越低;随着混凝土强度的提高,构件破坏时纵筋的应变越小,纵筋达到屈服时越接近构件破坏时间.构件SRHC-5相较于构件SRHC-2,破坏时纵筋应变减小41%,进而说明混凝土强度对构件最终承载力影响显著;SRHC-7相较于构件SRHC-2、SRHC-6,加载过程中纵筋应变一直滞后,最终破坏时纵筋应变相差不大.

图6 轴向载荷应变曲线
2.3.3 混凝土应变
构件SRHC-1~SRHC-7破坏截面处,混凝土截面的应变随轴向载荷的变化规律如图7所示.根据文献[12]混凝土破坏压应变约为 0. 002时认为混凝土破坏,而SRHC-3、SRHC-5两个构件破坏时,构件破坏截面混凝土表面应变均未达到0.002,故认为这两个柱破坏时,混凝土都没有达到预期强度.SRHC-2、SRHC-3相对于SRHC-1,混凝土应变分别减小2.8%,13.2%.由此可知,初始负载越大,构件破坏时混凝土应变越小,因为型钢的初始负载较大,当再对构件进行加载时,轴向载荷大多数由型钢所承担,导致其变形减弱,而使构件整体的抵御变形的能力减弱,虽然加载时分布在外部钢筋混凝土上的轴向载荷很少,其也很快被压碎;根据SRHC-4、SRHC-2、SRHC-5变化规律,随着混凝土强度的提高,在加固柱破坏时,混凝土发生的应变也就越小;由SRHC-2、SRHC-6、SRHC-7的混凝土应变变化规律可知,箍筋直径越大,构件破坏时混凝土应变越大,SRHC-6、SRHC-7相对于SRHC-2分别提高20.2%和26.68%,这是由于配筋率越大,混凝土越能被充分利用.

图7 轴向载荷应变曲线
2.3.4 型钢应变
根据图8可知,构件达到峰值载荷时,型钢受压承载能力充分发挥.构件SRHC-3柱中,型钢应变一直超前于其他构件,说明初始负载越大,型钢应变越超前;初始负载大小相同的构件,混凝土强度高能延缓型钢应力超前的现象,但是配箍率大小对此现象影响不大.

图8 轴向载荷应变曲线
3 轴压承载力计算
3.1 构件各部分承担的轴力分析
初始负载大小控制在一定范围内时,加固柱的破坏形态类似于零负载下的型钢混凝土柱,且最终破坏时钢筋和型钢均屈服.可参照我国YB9082—2006《钢骨混凝土结构技术规程》[13-14],按叠加法来计算此类加固柱的轴心受压承载力.
(1) 被加固柱的破坏标志
假设进行加固前型钢压应变为εss1,加固后二次加载时,εss1达到型钢的极限压应变εssu时,型钢首先屈服退出工作,新增钢筋混凝土部分可继续承受载荷至破坏.当构件达到能承受的极限受压载荷时,型钢应力达到fssu,而假设钢筋和混凝土的应力分别达到σc、σy,由于存在应变滞后现象,σc和σy可能均达不到各自的极限强度值fc、fy,其值取决于εssu和εss1的差值Δεss=εssu-εss1.Δεss越大,σc和σy就越接近其相应的极限强度值,当Δεss=εssu时,相当于零负载型钢混凝土柱,σc和σy均可达到各自的极限强度值;当Δεss=0时,加固时型钢已达极限破坏状态,钢筋混凝土部分已经基本起不上作用.
(2) 基本假定
① 加固后,新加混凝土与原钢柱为理想情况,符合平截面假定;
② 不考虑混凝土拉应力,混凝土的应力-应变关系采用ACI 规范中的Hognestad假定;
上升段抛物线:εc≤ε0,
(1)
下降段直线:εc>ε0,
(2)
式中:εu为极限压应变,一般取0.003 8.
③ 假定钢筋和型钢都为理想的弹塑性材料.其本构关系表达式如下:
(3)
式中:σs为型钢和钢筋的应力;εs为应力为σs时对应的应变;Es、fy、εy为型钢和钢筋的弹性模量、屈服强度、应力为fy时的应变.
④ 柱长度方向,截面曲率相同,各截面所受轴力相同.
3.2 轴压承载力计算方法
计算加固柱承载力, 可以分别计算型钢、 钢筋混凝土所能承担的轴向力, 然后将二者累加, 即得构件的极限承载力.其中型钢所承担的轴向压力可表示为
(4)
钢筋混凝土所承担的轴向压力为
(5)
因此,加固柱的承载力计算公式为
(6)
式(6)仅适用于初始负载应力较小的轴压加固柱.试验表明,钢柱在加固前,若所承受的载荷未使其进入塑性工作阶段时,完全卸载后再加固,加固后的组合柱仍可按普通型钢混凝土柱进行计算.但在负载状态下加固时,钢筋混凝土应变可能一直滞后于型钢,型钢先受力屈服后,钢筋混凝土很快就破坏,因此计算最终承载力时,需对混凝土和纵向钢筋进行强度折减.
依据Hognestad假定,混凝土达到最大强度前的应力-应变关系为
(7)
为方便地按零负载型钢混凝土柱来计算承载力,对负载下外包混凝土加固柱,参考各国学者对混凝土结构加固试验的研究,将混凝土和钢筋的强度折减系数的计算公式如下.
加固前:
(8)

(9)
式中:N1为加固前型钢一期载荷值;σss1为加固时型钢截面的应力;Ass为型钢的有效净面积;Ess为型钢的弹性模量;β为型钢初始负载应力水平指标;εssu为型钢柱极限压应变;εss1为加固前型钢压应变;fssu为型钢极限抗压强度;ρss为型钢稳定系数.
加固柱破坏后:
(10)
(11)
(12)
(13)
(14)
式中:Nu为加固柱最终极限承载力;φ为加固柱的整体稳定系数;σy为加固柱破坏时钢筋的压应力;As为纵向受压钢筋的截面积;σc为加固柱破坏时混凝土的压应力;Ac为混凝土的净截面积;αy为纵筋强度折减系数,当αy>1时, 取αy=1;αc为混凝土强度折减系数;εc0为混凝土极限抗压应变,一般取εc0=0.002;Ey为纵向钢筋的弹性模量.
图9为αy、αc随β的变化曲线,当β=1时,αy=αc=0,说明型钢已屈服时无需再加固;当β=0时, αy=αc=1,可以按照零负载柱进行计算.
将式(14)、式(12)带入式(10),可得到加固柱的承载力计算公式:
(15)
式中,fy为纵向钢筋抗压屈服强度;fc为混凝土抗压强度标准值.
式中αy和αc的取值是随着β的变化而变化的,相对于原来叠加法中折减系数取定值0.8有了一定准确性的提升.

图9 加固柱αy、αc和β的曲线
3.3 计算值与试验值的比较
将试验数据代入式(15)可以计算出轴心受压承载力,计算值与试验值的比较见表3.
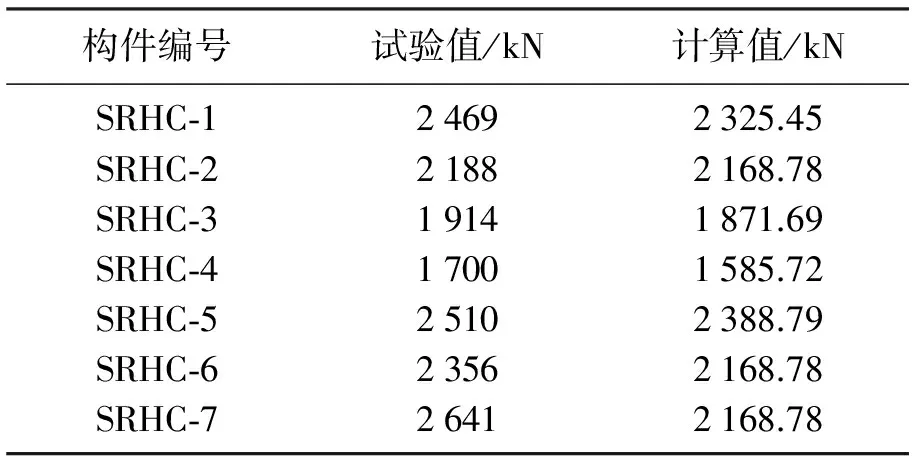
表3 试验值与计算值的比较
由表3可见SRHC-1~SRHC-5五个构件的试验值、理论计算值吻合较好,说明本文所给的加固柱的轴心受压承载力计算公式合理可行.构件SRHC-6、SRHC-7未考虑构件约束作用,因此偏差大.
4 结 论
本文研究了3种混凝土强度、3种初始负载应力大小及3种箍筋直径的加固柱,对其进行受压实验,将实验值与计算值作比较,得出以下结论:
(1) 利用外包钢筋混凝土法加固轴压钢柱构是一种新型的钢结构加固方式,加固后的组合柱与普通型钢混凝土组合结构的受力具有相似之处;加固后钢-混凝土组合柱轴心受压承载力明显提高,稳定性明显增强,各截面大致符合平截面假定;本文计算方法较为实际可行.
(2) 由试验发现,随着初始负载应力的增加,加固后钢-混凝土组合柱的轴心受压承载力降低明显,新增加固材料强度利用率越低,因此,钢结构加固时,应尽量对原结构进行卸载,以使初始负载应力尽量减小,从而使加固后钢-混凝土柱完全能够满足结构或构件的使用要求;加固后钢-混凝土组合柱的承载力随混凝土强度提高而增大,轴向位移减小;随着箍筋直径的增大,构件承载力和新增钢筋混凝土应变逐渐增大,但是对轴向位移影响不明显.
(3) 对实验进行分析可得,加固后的组合结构其结合能力稍差,对于如何加强结构结合能力,提升加固效果,还需进一步研究.
[ 1 ] 陈宗平,应武挡,陈宇良. 型钢再生混凝土柱的正截面极限承载力计算[J]. 混凝土, 2013(10):10-13. (CHEN Z P,YING W D,CHEN Y L. Research on the ultimate bearing capacity calculation of steel reinforced recycled concrete columns[J]. Concrete, 2013(10):10-13.)
[ 2 ] 赵永宏. 型钢混凝土异形框架柱正截面承载力研究[D]. 西安: 西安建筑科技大学, 2007:4. (ZHAO Y H. Study on bearing capacity for SRC special shaped columns[D]. Xi’an: Xi’an University of Architecture and Technology, 2007:4.)
[ 3 ] 李惠,王震宇,吴波. 钢管高强混凝土叠合柱抗震性能与受力机理的试验研究[J]. 地震工程与工程振动, 1999,19(3):27-33. (LI H, WANG Z Y, WU B. Experimental research on mechanism and seismic performance of laminated column with steel tube filled with high-strength concrete[J]. Earthquake Engineering and Engineering Vibration, 1999,19(3):27-33.)
[ 4 ] 李惠,王震宇,吴波. 钢管高强混凝土叠合柱弯矩一曲率关系的合成模型[J]. 计算力学学报, 2000,17(2):184-191. (LI H, WANG Z Y, WU B. Model of moment-curvature relationship of laminated column with high-strength concrete filled steel tube[J]. Chinese Journal of Computational Mechanics, 2000,17(2):184-191.)
[ 5 ] 佘俊. 预压型钢混凝土柱受力性能分析[D]. 长沙:长沙理工大学, 2010:40. (SHE J. Mechanics analysis on steel reinforced concrete columns of precompressed stress[D]. Changsha:Changsha University of Science & Technology, 2010:40.)
[ 6 ] 李国芳. 预压型钢混凝土柱力学性能有限元分析[D]. 长沙:长沙理工大学, 2008:31-40. (LI G F. The finite element analysis on mechanics performance of steel reinforced concrete columns of precompressed stress[D]. Changsha:Changsha University of Science & Technology, 2008:31-40.)
[ 7 ] 王元清,周晖,胡宗文,等. 钢结构厚板力学性能的低温试验研究[J]. 土木建筑与环境工程, 2011,33(5):7-12. (WANG Y Q, Zhou H, HU Z W et al. Experimental analysis of mechanical properties of thick plate in steel structure at low temperature[J]. Journal of Civil Architectural & Environmental Engineering, 2011,33(5):7-12.)
[ 8 ] 许成祥,李忠献,蔡卫东. 考虑二次受力碳纤维布加固短柱的抗震试验[J]. 武汉理工大学学报, 2002,24(7):27-30. (XU C X, LI Z X, CAI W D. Experimental research on seismic behavior of RC short columns strengthened with fiber sheets based on the characteristic of two-stay load[J]. Journal of Wuhan University of Technology, 2002,24(7):27-30.)
[ 9 ] 季强,苏三庆,张心斌. 用外包钢筋混凝土法加固RC柱性能的试验研究[J]. 工业建筑, 2005(s1):945-947. (JI Q, SU S Q, ZHANG X B. An experimental study on behavior of RC columns strengthened with enclosed reinforced concrete[J]. Industrial Construction, 2005(z1):945-947.)
[10] 张曦. 方钢管约束型钢混凝土与钢筋混凝土短柱抗震性能试验研究[D]. 哈尔滨:哈尔滨工业大学, 2009:36-37. (ZHANG X. Experimental research on seismic behavior of square steel tube confined SRC and RC short columns[D]. Harbin: Harbin Institute of Technology, 2009:36-37.)
[11] 李俊华,薛建阳,王新堂,等. 反复载荷下型钢混凝土柱粘结滑移性能试验研究[J]. 工程力学, 2009,30(4):211-218. (LI J H, XUE J M, Wang X T, et al. Experimental study on bond-slip behavior in SRC columns under cyclic reversed loading[J]. Engineering Mechanics, 2009,30(4):211-218.)
[12] 刘靓. 加固轴压混凝土柱的有限元及可靠度分析[D]. 哈尔滨:哈尔滨工业大学, 2013:27-31. (LIU L. Finite element analysis and reliability analysis of reinforced concrete columns under axial compression[D]. Harbin: Harbin Institute of Technology, 2013:27-31.)
[13] 刘祖强,薛建阳,马辉,等. 型钢再生混凝土柱正截面承载力试验及数值模拟[J]. 工程力学, 2005,32(1):81-87. (LIU Z Q, XUE J Y, MA H et al. Testing and numerical simulation of the normal cross-section bearing capacity of steel reinforced recycled concrete columns[J]. Engineering Mechanics, 2005,32(1):81-87.)
[14] CHEN C, LIN N. Analytical model for predicting axial capacity and behavior of concrete encased steel composite stub columns[J]. Journal of Constructional Steel Research, 2006,62(5):424-433.
【责任编辑: 赵 炬】
Axial Compression Behavior of Column While under Load
ZhouLe,NieXiaomei,WangKeyao,ZhengYuan
(School of Architecture and Civil Engineering, Shenyang University, Shenyang 110044, China)
In order to further research the mechanical properties of reinforced columns, experiments of seven reinforced columns and one steel column under monotonic axial compression are carried out. Three related parameters, the initial load size, concrete strength and stirrup diameter, are concerned. The failure patterns, load-displacement curves, and load-strain curves are obtained. The influences of three parameters on axial compression behavior are analyzed. The formula for axial compression load of reinforced column is presented. The results show that the bearing capacity of the column increases significantly with the increase of stirrup ratio and concrete strength. The strain hysteresis of reinforced concrete becomes greater and the load-carrying capacity becomes lower with the increase of initial load. A certain reduction should be done for the new materials in the calculation of axial compression bearing capacity of the reinforced column.
reinforced column; axial compression behavior; strain hysteresis; ultimate bearing capacity
2016-11-17
国家自然科学基金资助项目(51408371); 辽宁省自然科学基金资助项目(2014020098).
周 乐(1978-),女,辽宁营口人,沈阳大学教授,博士,硕士研究生导师.
2095-5456(2017)02-0132-09
TU 375.3
A

