带有机器卸载不延误约束的多吊机调度问题

谢 谢, 郑勇跃

(1. 沈阳大学 装备制造综合自动化重点实验室, 辽宁 沈阳 110044; (2. 辽宁省标准化研究院, 辽宁 沈阳 110004)



带有机器卸载不延误约束的多吊机调度问题

谢 谢1, 郑勇跃2

(1. 沈阳大学 装备制造综合自动化重点实验室, 辽宁 沈阳 110044; (2. 辽宁省标准化研究院, 辽宁 沈阳 110004)

针对钢铁企业冷轧阶段罩式退火过程,考虑了一类带有机器卸载不延误约束的多吊机调度问题.给出了避免吊机碰撞和保证机器卸载不延误的一些可行性质.基于这些性质,提出了一个启发式算法,该算法的计算复杂性与吊机、工件和机器的数目有关.同时,给出了问题的一个下界.分别通过理论分析和计算实验,证明了启发式算法的最坏性能和平均性能.

罩式退火过程; 吊机调度; 强NP难; 启发式算法; 最坏性能分析

钢铁企业的冷轧生产的罩式退火过程是冷轧板卷后道工序生产的常见的模式,经过该过程可以生产出高附加值的产品.每垛板卷预先放在一个固定的炉台上进行两阶段处理.第一阶段为加热,第二阶段为冷却.一台加热机器(加热罩)和一台冷却机器(冷却罩)被移动到这个工件的位置依次进行加热操作和冷却操作.为了方便描述,每垛板卷定义为一个工件.不同于经典的两阶段流水作业的问题,每个工件需要通过两台固定机器,这个过程如图1所示.机器的移动都由上方移动的吊机实施.一旦一台机器(加热罩或冷却罩)被装载到工件上,加工(加热或冷却)立即开始.当加工达到一个预设的值(加热时间或冷却时间),机器必须被立刻卸载以停止进一步的加工.也就是说,第一阶段一旦板卷温度达到设定值,加热罩必须移走以停止加工.类似的,第二阶段一旦板卷温度降低到某设定值,冷却罩必须移走以停止加工.任何机器卸载额外的延迟都会导致工件质量的不足.因此,机器卸载不延误约束对于增加钢铁企业机器利用率、改进生产率能量利用率、降低生产费用非常关键.可以通过有效的生产计划和调度来实现.

图1 罩式退火过程

然而,同一工件两阶段加工之间没有时间限制.当冷却罩从工件上卸载,意味着工件退火过程的结束.由吊机将机器从一个位置移动到另一个位置称为吊机的装载移动.一个装载移动包括从机器的位置提起它,移动到另一个位置后将它放下.实施装载移动的操作后,吊机需要空移动到一个适合的位置实施下一个装载移动.显然,吊机负责将机器从一个工件移动到另一个工件保证对工件进行每阶段的加工.因此,罩式退火系统的生产率大大依赖于有效的吊机调度.

实际生产中罩式退火车间的炉台按列排好,每列具有相同数目的炉台,均匀地位于其中.一个炉台的位置可以独一无二地使用它的列号(x坐标)和行号(y坐标)表示.图2给出了罩式退火车间的俯视图,图中各吊机共用一个相同的跨.一个吊机的桥可以沿着跨到达不同的列,吊钩可以沿着桥移动到每一列中不同的位置.这样的结构使得吊机间不能彼此相互跨越.在任意两个相邻吊机之间有一个最小安全距离的要求以避免两相邻吊机之间可能的碰撞.因此,同一列中的炉台不能由两个或多个吊机同时服务.本文研究的是具有机器卸载不延误约束(固定的加热和冷却时间)和吊机之间不碰撞的多吊机调度问题.这个问题包括分配和调度两种机器以加工工件和调度吊机在工件之间移动工件.目标为最小化车间内最后一个工件的完工时间.

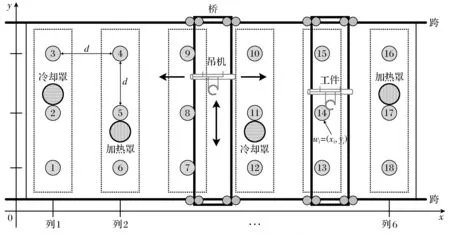
图2 罩式退火车间的俯视图

本文所研究的问题考虑了罩式退火系统中吊机调度和机器分配的组合.已有的有关罩式退火过程中吊机调度的研究主要是决策单吊机调度.然而,Catherine等人[1], Moon和Hrymak[2],Liu等人[3]并没有考虑吊机移动的细节以及调度过程中每个机器的具体位置.由于任何延误时间都会导致产品密度和韧性的改变,本文研究的是机器卸载不延误约束的生产模式.此外,在这个钢铁的退火系统中即使不考虑机器卸载不延误约束,Tang等人[4]研究了单吊机调度问题,Xie和Tang[5]以及谢和李[6]研究了多吊机调度问题,其中,Xie和Tang[5]致力于考虑机器预先分配的问题,然而,并没有对多吊机操作进行理论分析.谢和李[6]并没有考虑机器卸载不延误约束的多吊机调度问题.为避免吊机干涉使用同样的方法鉴别问题的可行性质和最优性质,Xie等人[7]对钢卷仓库内的多吊机调度问题进行了研究,谢和李[8]考虑了运输与倒垛集成的多吊机调度问题.然而现有文章几乎很少考虑本文研究的问题,文献[9-10]考虑了本文所研究问题的简化版本,但他们忽略了吊机沿跨和桥移动时的装载移动和空载移动.此外,他们没有给出问题的数学模型,算法的最坏性能界也仅和吊机工件的数目有关,而和吊机移动时间无关,本文改进了该界.尽管Tang等人[11]的研究和罩式退火过程相关,但主要考虑的是分批问题而不是吊机的调度过程.因此,大部分研究的方法不能直接应用于罩式退火过程中机器卸载不延误的多吊机调度,很有必要研究这类新的吊机调度问题.

1 问题的定义和描述

给定n个需要加工工件的集合Ω={1,2,…,n},每个工件已经放在了固定的炉台上.工件i的位置为wi,这个位置可以由它所在炉台的位置、车间中独一无二的坐标(xi,yi)表示.用R表示车间中列的集合,从左至右沿着x轴依次标号1,2,…, |R|,因此工件的集合可以分成|R|个子集Ω1,Ω2, …,Ω|R|,其中Ωr为列r中的工件集合.令L表示每个列中炉台的个数,如图2所示,以|R|=10和L=3为例的车间俯视图.将处在同一y轴的工件表示为(•,yi),同一x轴的工件表示为(xi,•).相邻两列之间的距离以及同一列中相邻炉台之间的距离为d.定义吊机的位置是它的吊钩向地面投影的位置.如果机器正在加工工件,它的位置就是这个工件的位置.否则,它的位置为与它距离最近的工件的位置.所有的工件、机器和吊机从0时刻可获得.

为了便于参阅,将上文提到的全部符号排列如下,一些需要进一步使用的符号将在需要的时候给予定义.

Ω—需要加工工件的集合;

n—需要加工工件的数量;

wi—工件i的位置,也可以用坐标(xi,yi)表示;

R—车间中列的集合,从左至右延着x轴依次标号1, 2, …, |R|;

Ωr—列r中的工件集合;

L—每个列中炉台的个数;

d—相邻两列之间的距离以及同一列中相邻炉台之间的距离;

M—机器的集合M={1, 2, …,|F|,|F|+1, …,|F|+|C|},包括|F|个相同的加热罩以及|C|个相同的冷却罩;

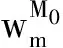
pi1和pi2—每个工件i(i∈Ω)的加热和冷却时间;

H—吊机的集合;

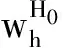
μ—上提时间和下放时间;

v1和v2—吊机沿跨移动和沿跨间移动的速度;

λ1和λ2—吊机沿跨移动和沿跨间空移动的速度,其中(λ1≥v1),(λ2≥v2);

2 可行解的性质

2.1 吊机分配不碰撞约束

根据吊机所在位置以及吊机间安全距离的要求,如果一个工件在车间中某列且距离最左侧位置的距离小于d,则这列中的全部工件仅可由吊机1服务.类似地,如果一个工件在车间中某列且距离最左侧位置的距离小于2d,则这列中的工件仅可由吊机1或2服务.因此令Xi(1≤Xi≤|H|)表示服务于工件i的吊机号(∀i∈Ω),可得到如下性质.

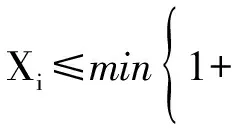
(1)

类似地,根据跨最右侧的位置(xl,·),吊机的分配决策有如下表达:

(2)

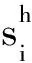
性质2 为避免吊机在相邻两列的冲突,对于任意的r∈R,i∈Ωr,i′,j∈Ωr+1,两吊机h,h+1∈H操作的情况如下:

情况1(见图3a) 可行操作满足以下安全距离的要求:当吊机h完成对列Ωr中工件i的装载操作后,空移动到列Ωr+1中对工件i′操作的时间不早于吊机h+1完成对列Ωr+1中工件j的装载操作.因此,一定有

(3)

情况2(见图3b) 可行操作满足以下安全距离的要求: 当吊机h开始从列Ωr中工件i到列Ωr+1中工件i′装载操作的时间不早于吊机h+1完成对列Ωr+1中工件j的装载操作. 因此, 一定有

(4)

情况3(见图3c) 可行操作满足以下安全距离的要求:当吊机h完成对列Ωr中工件i的装载操作后,空移动到列Ωr+1中对工件i′操作的时间不早于吊机h+1开始对列Ωr+1中工件j的装载操作.因此,一定有

(5)

情况4(见图3d) 可行操作满足以下安全距离的要求:当吊机h开始从列Ωr中工件i到列Ωr+1中工件i′装载操作的时间不早于吊机h+1开始对列Ωr+1中工件j的装载操作.因此,一定有

(6)

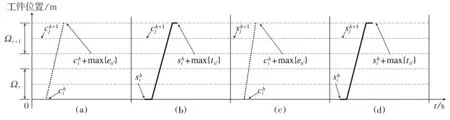
图3 相邻列中避免吊机冲突的说明

性质3 为避免吊机在同列中的冲突,对任意r∈R,i,i′,j∈Ωr相邻吊机h,h+1∈H操作的各情况如下:

情况1(见图4a) 对任意同列中的工件i,i′和j,可行操作满足安全距离的要求,当吊机h+1开始从工件i′到工件i装载的开始时间不早于吊机h从工件j装载的开始时间,一定有

(7)

情况2(见图4b) 对任意同列中的工件i,i′和j,可行操作满足安全距离的要求,当吊机h+1开始从工件i′空移动之后对工件i完成装载移动的时间不早于吊机h从工件j装载的开始时间,一定有

(8)

图4 同列中避免吊机冲突的说明

情况3(见图4c) 对任意同列中的工件i,i′和j,可行操作满足安全距离的要求,当吊机h+1开始从工件i′到工件i装载的开始时间不早于吊机h对工件j完成装载移动的时间,一定有

(9)

情况4(见图4d) 对任意同列中的工件i,i′和j,可行操作满足安全距离的要求,当吊机h+1开始从工件i′空移动之后对工件i完成装载移动的时间不早于吊机h对工件j装载移动的完成时间,一定有

(10)

2.2 机器卸载不延误约束

为了保证机器卸载不延误约束,下面的性质分别针对吊机为同一列和不同列中工件卸载机器的时间要求.

性质4 如果同一列中的两工件i和j同时需要吊机卸载机器,则两个工件某一操作(加热或冷却)的完工时间之差不能少于

(11)

性质5 如果不同列中的两工件i和j同时需要吊机卸载机器,则两个工件某一操作(加热或冷却)的完工时间之差不能少于

(12)

3 启发式算法

根据工件i (i∈Ω)两阶段加工时间的总和pi1+pi2非增排序,形成列表JList;

只要列表JList不空,算法如下进行

{

如果机器可获得且存在未完成退火过程的工件,则为工件分配吊机操作当前可获得的尽可能多的机器;

如果存在一台可获得的吊机,且两个或更多需要吊机同时操作为其装载的工件,则选择可以最早开始加工的工件(选择距离吊机当前距离最近的工件);

如果存在两个或更多需要吊机同时装载或卸载机器,则优先分配给需要卸载的机器以完成加工的工件;

如果如果两个或多个吊机空闲同时可利用,则选择具有最短总距离(如果工件正在加工则总距离为吊机从当前位置到该工件的距离;如果工件正等待机器,则总距离为吊机从当前位置到机器再到工件的距离)的吊机; 否则根据性质1即公式(1)、(2)检验当前分配的吊机编码是否在可行范围内;进一步为避免吊机冲突,根据性质2即公式(3)～公式(6),性质3即公式(7)～公式(10)分别检验相邻两列和同一列中工件在每种情况下的可行性;

如果可行,则构建吊机排序;

否则,交换吊机间的操作,或一台吊机等待直到另一台吊机完成当前操作;

否则为保证机器卸载不延误约束,根据性质4即公式(11)和性质5即公式(12)分别检验同列和不同列的每种可行性;

如果可行,则构建吊机排序;

否则,交换吊机间的操作,或一台吊机等待直到另一台吊机完成当前操作;

否则,一旦相同,选择当前需要最长加工时间的工件;

否则,删除退火完成的工件;

}

结束

工件初始化的排序耗时时间O(nlogn).为避免吊机冲突,检验可行的吊机操作时间为O(n|H|).为保证机器卸载不延误约束,检验可行加热罩和冷却罩的操作最多耗时分别为O(n2|H||F|)和O(n2|H||C|),因此,启发式算法的复杂度为O(n3|H|(|F|+|C|)).

4 最坏情况分析

为了分析算法的最坏性能比,首先提出了下界.由于几个下界之间互相补充,没有一个能代替另一个.进一步采用复合下界的策略,使得到的问题的下界可以更接近最优值.分析了问题启发式的最坏性能,也根据机器数目不同的三种情况得到了三个界.

性质6 问题的下界LB可由下面的三个表达式获得:

其中,LB=max{LB1, LB2, LB3}.

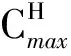
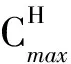
于是有

5 数值计算实验与结果

在这部分中,对所提出的启发式算法进行实验以检验其有效性.这个算法由C语言编程,在Pentium-Ⅳ的PC机上运行,操作系统是WindowsXP,CPU是2.40GHz.根据罩式退火过程的实际生产,测试问题所用到的参数利用以下方式随机产生.

吊机的数目(|H|):2;

工件的数目(n):9=3×3,15=3×5,18=3×6,20=4×5,24=4×6,30=5×6;

加热罩的数目(|F|)和冷却罩的数目(|C|):在[10,30]之间离散平均分布随机生成;

装载移动速度(v=max{v1,v2}),空移动速度(λ=max{λ1,λ2}),提起和下放的时间(μ),在[1,5]之间离散平均分布随机生成,此计算实例中,取v=1,λ=2,μ=1;

两相邻炉台间的距离(d):在[1,10]之间离散平均分布随机生成,此计算实例中,取d=4;由此可计算任意两工件之间装载移动时间tij和空移动时间eij.

工件的加热时间(pi1)和冷却时间(pi2):分别在[1,10]、[1,30]、[1,50]和[1,100]之间离散平均分布随机生成;

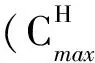
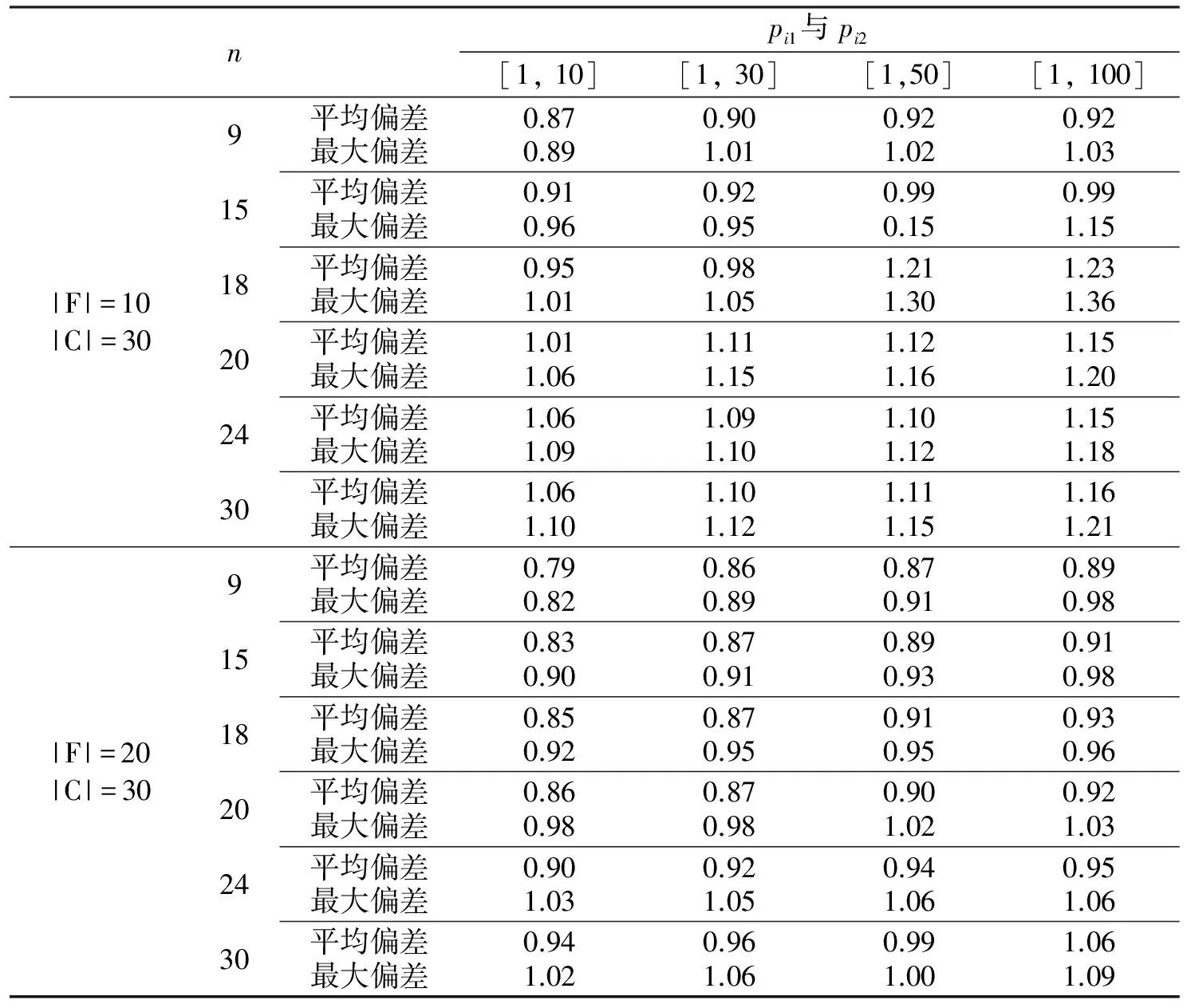
表1 启发式算法性能计算实验结果

数值计算结果表明,当加热罩冷却罩的数量越充足,启发式得到的平均偏差越小,这是因为减少了吊机、工件不必要的等待时间.此外,加热时间和冷却时间越短,便于越早的释放这两类加工机器,使得可利用的机器数量充足,同样启发式得到的偏差也减少.可以解释为加热罩、冷却罩为两类瓶颈设备.因此有效的吊机调度可以优化这两类设备的使用,从而提高生产率和客户满意度.

6 结 论

本文研究一类罩式退火过程中机器卸载不延误的多吊机调度问题.分析了问题的可行性质以避免吊机冲突以及保证了机器卸载的不延误,进一步提出一个启发式算法并进行了最坏情况分析.未来的研究中,将继续考虑钢铁企业其他相 似生产背景中,如罩式退火操作、连续退火操作和热镀锌过程的吊机调度、以及吊机与其他运输工具的联合运输.

[ 1 ] AZZARO-PANTEL C, BERNAL-HARO L, BAUDET P, et al. A two-stage methodology for short-term batch plant scheduling: discrete-event simulation and generic algorithm[J]. Computers & Chemical Engineering, 1998,22(10):1461-1481.

[ 2 ] MOON S, HRYMAK A N. Scheduling of the batch annealing process: deterministic case[J]. Computers & Chemical Engineering, 1999,23(9):1193-1208.

[ 3 ] LIU Q L, WANG W, ZHAN H R, et al. Optimal scheduling method for bell-type batch annealing shop and its application[J]. Control Engineering Practice, 2005,13(10):1315-1325.

[ 4 ] TANG L X, XIE X, LIU J Y. Scheduling of a single crane in batch annealing process[J]. Computers & Operations Research, 2009,36(10):2853-2865.

[ 5 ] XIE X, TANG L X. Crane scheduling in batch annealing process[C]∥Proceedings of the IEEE International Conference on Automation and Logistics, 1-3 Sept, 2008, Qingdao. IEEE, 2008:2020-2025.

[ 6 ] 谢谢,李彦平. 罩式退火过程中的多吊机调度问题[J]. 沈阳大学学报(自然科学版), 2012, 24(1):12-19. (XIE X, LI Y P. Multi-crane scheduling in batch annealing process[J]. Journal of Shenyang University(Natural Science), 2012,24(1):12-19.)

[ 7 ] XIE X, ZHENG Y Y, LI Y P. Multi-crane scheduling in steel coil warehouse[J]. Expert Systems with Applications, 2014,41(6):2874-2885.

[ 8 ] 谢谢,李彦平. 运输与倒垛集成的多吊机调度问题[J]. 沈阳大学学报(自然科学版), 2014, 26(3):210-217. (XIE X, LI Y P. Coordinate transportation and shuffling operations in multi-crane scheduling problem[J]. Journal of Shenyang University(Natural Science), 2014,26(3):210-217.)

[ 9 ] XIE X, KONG X Y, ZHENG Y Y, et al. A heuristic algorithm for solving multi-crane scheduling problem in batch annealing process[J]. Applied Mechanics and Materials, 2014,620:179-182.

[10] XIE X, LI Y P, ZHENG Y Y. Multiple crane scheduling in batch annealing process with no-delay constraints for machine unloading[C]∥IEEE International Conference on Information and Automation, 6-8 June, 2012, Shenyang. IEEE, 2012:597-601.

[11] TANG L X, MENG Y, CHEN Z L, et al. Coil batching to improve productivity and energy utilization in steel production[J]. Manufacturing & Service Operations Management, 2015,18(2):1-18.

【责任编辑: 李 艳】

Multiple Crane Scheduling with No-Delay Constraints for Machine Unloading

XieXie1,ZhengYongyue2

(1.Key Laboratory of Manufacturing Industrial and Integrated Automation, Shenyang University, Shenyang 110044, China; 2 Liaoning Institute of Standardization, Shenyang 110004, China)

Aiming at the problem that arises in the batch annealing process in the cold rolling stage of steel production, a multiple crane scheduling problem with no-delay constraints for machine unloading is studied. Some feasible properties are identified to avoid crane collisions and guarantee machine unloading no-delay constraints. Based on these necessary conditions, a heuristic algorithm with running time in connection with the number of cranes, coils and machines is presented. A lower bound to the problem is also developed. Through the theoretically analysis and computational experiments, the worst case bound and the average performance of the heuristic algorithm are proved.

batch annealing process; crane scheduling; strongly NP-hard; heuristic algorithm; worst case analysis

2016-11-28

国家自然科学基金资助项目(71672117); 辽宁省自然科学基金资助项目(201602526); 辽宁省高等学校杰出青年学者成长计划资助项目(LJQ2014133).

谢 谢(1981-),女,辽宁沈阳人,沈阳大学副教授,博士.

2095-5456(2017)02-0118-07

TP 301.6

A