气枪立体震源等效深度确定方法研究

刘雪芹， 刘怀山， 尉 佳

(中国海洋大学 海底科学与探测技术教育部重点实验室，青岛 266100)

气枪立体震源等效深度确定方法研究

刘雪芹， 刘怀山， 尉 佳

(中国海洋大学 海底科学与探测技术教育部重点实验室，青岛 266100)

目前地震勘探气枪立体震源等效深度确定没有一个标定根据，为了与常规气枪阵列进行对比，需对气枪立体震源等效深度有一个最佳确定方法。基于实际条件下的气枪模拟方法，这里对具有代表性的多种阵列进行了模拟，研究了几何加权法和频率陷波法两种等效深度求取方法，重点分析了频率陷波法的影响因素；然后又结合实际数据进行了实际应用分析，提出了实际生产中的等效深度有效求取方法。

子波模拟； 几何加权； 频率陷波； 等效深度

0 引言

气枪是海上地震勘探重要的人工震源,对于海上高精度地震勘探，震源研究有着极其重要的意义。Chelminski[1]首次发明并测试用于地震勘探的气枪震源，早期气枪震源一般为压力与容量较大的单枪震源；1970年，Ziolkowski[2]，Schulze-Gattermann[3]和Safar[4]对气枪激发物理过程、运行机制进行了相关研究，并发展了模拟气枪远场信号的理论。为克服单枪震源信号的一些缺陷，不同容量单枪组合成的组合震源调谐阵列应运而生，调谐阵列具有宽频，能量大等优势，从此，气枪逐渐成为海洋地震勘探的主要震源[5-7]。

在气枪被引入地震勘探行业之后，许多地球物理学家对其进行研究以建立气枪信号模拟模型。Ziolkowski[2]研究了气枪激发的物理过程，并基于Gilmore理论基础上，运用了Kirwood和Bethe的近似方法，提出预测气枪信号波形的理论，建立了第一个单枪子波模型；Schulze-Gattermann[3]讨论了气枪运作过程，以及气枪本身的存在对气枪压力信号频率的影响，同样也建立了单枪信号的模拟模型；Safar[4]提出了预测子波信号的振幅、气泡周期的公式；Johnson[8]提出一个简化的气枪子波模型，将气泡振荡过程等效于弹簧振子的阻尼振动过程，得到的模拟信号与Ziolkowski模型模拟结果非常接近；Ziolkowski[9]后来推导出了一个气枪子波模拟的算法，可以在已知波场中任意一点压力变化的情况下推出其他任意位置的压力信号；MacGillivray[10]、Li[11]等在Ziolkowski模型的基础上，综合考虑了影响气枪子波波形的各种因素，包括枪口节流、精确的热传递以及气泡上浮等，提出一较为准确的气枪子波模型；王立明[12]则认为由于一般气枪气室的初始压力很大，超出了理想气体状态方程的适用条件，于是引入了范德瓦尔斯气体方程，并综合考虑多种影响因素，得到了更为精确的子波模拟模型。

在海上地震勘探中，震源虚反射的存在一直限制着资料的频带宽度与分辨率，阻碍着高分辨率地下成像的发展。Moldoveanu[13]指出上、下两层震源技术可以用来去除鬼波；Parkes等[14]提出通过将震源置于不同深度交替激发而获得互补的地震资料来实现上下行波场的分离，最终可以修复气枪子波频谱[15]。但是由于交替激发使获得的地震资料反映的位置不同，因此并不能达到理想的条件。还有一种方案就是将两个深度的震源同时激发，然后将其分离并进行反鬼波。但这种方法也会因为上下震源激发的不同步而导致低频分离困难[16]。 Hopperstad等[17]提出了立体延时阵列设计以及气枪阵列时延技术；Cambois等[18]进一步研究了立体震源采集的原则和设计因素，将陆上地震勘探中的延时叠加震源技术应用到海上地震勘探中，将气枪布置在不同的深度进行延时激发。这项技术只需要对现有的枪阵进行很小地改动，最终产生的波场并不是各向同性的，需要进一步的改进。之后改进的海上气枪立体震源有两侧对称的凹形立体枪阵和凸形立体枪阵等[19]。

立体震源已广泛应用于海上数据采集工作，在过去的研究中并没有将立体震源作为一个整体研究其相关参数。立体震源中子阵呈不同深度，不同形状排列。为了便于以后更加系统地描述立体震源，并进行进一步的震源整体性能研究，笔者首先以深度参数角度，基于实际气体条件下范氏方程气枪子波模拟方法，对具有代表性的多种阵列进行了模拟，研究了几何加权法和频率陷波法两种等效深度求取方法，重点分析了陷频频陷法的影响因素；然后又结合实际数据进行了实际应用分析，提出了实际生产中的等效深度有效求取方法。因此，可以将立体震源看成一个整体，对立体枪阵等效深度的参数确定提供了依据。

1 单枪震源各项参数与深度关系

1.1 频率陷波与深度的关系

气枪产生的直达波与震源虚反射都会被水听器接收到，二者有一定的时间延迟Δt，延迟时间与气枪的陈放深度有关。对于沿震源正下方传播的信号来说，其虚反射时间延迟为：

Δt=2h/vc

(1)

其中：h为震源的陈放深度；vc为海水中的声波速度。根据周期与频率的关系，由式(1)可得到式(2)。

f陷频=vc/2h

(2)

其中：f陷频表示气枪震源远场子波频率域陷频点对应的频率值。由式(2)可知，震源深度与陷频之间呈反比关系，该式中除此二者无其他未知参数，因此可以用式(2)作为研究立体震源等效深度的参考工具。

1.2 初泡比与深度的关系

子波的初泡比PBR与枪深D以及气枪容量v在2 000psi工作压力下的近似关系式为式(3)。

(3)

由式(3)可知，初泡比与枪深大体成反比关系，但在式(3)中除深度与初泡比之外，还存在可变参数气枪容量，由于在一个立体枪阵中会存在多种容量的气枪，若众多容量气枪的整体等效容量未知，就无法利用式(3)求取本文要求的等效深度。因此，运用式(3)进行相关的等效深度研究会比较复杂。

1.3 气泡周期与深度的关系

(4)

其中:枪深的单位为m，为常量，与气枪类型有关。

由式(4)可知，气泡周期与枪深大体成反比，但在式(4)中除深度与气泡周期之外，还存在可变参数压力值，运用式(4)进行相关的等效深度研究同样会比较复杂。

2 几何加权等效深度法

几何加权法是从立体几何角度出发来解释立体震源的等效深度。举例说明：一个物体摆在桌面上，物体高度即为它的重心点距离桌面的距离；几个物体摆在桌面上，其整体的高度即为它们共同的重心点距离桌面的距离。故可以从几何学角度来定义立体震源的等效深度。

同理，可以将不同深度的多个震源看做一个整体视之为一个震源，根据震源相干性原理，这一整体震源的容量即为所有震源容量之和，因此，笔者尝试将震源容量作为求取震源等效深度的权重，提出了加权法等效震源计算方法。加权法等效深度的计算方法是依据阵列中每个震源的容量作为权重，将其与对应震源深度相乘，然后叠加取平均，如式(5)所示。

(5)

其中：hi代表每个气枪震源陈放深度；n代表震源个数；vi代表每个气枪震源容量。

几何加权法计算立体震源的等效深度，只需立体震源的子阵深度和容量参数，因此，几何加权法求取的等效深度值是一个不随外界变化而变化的静态值。然而，实际野外采集环境存在多种干扰因素，所有的干扰因素都会影响立体震源的相关参数。因此，几何加权法求取的等效深度会存在一定误差。

3 频率陷波等效深度法

3.1 频率陷波法原理

由于单枪震源深度与初泡比，气泡周期的关系式中存在较多其他未知参数，使等效深度的变化规律复杂化，加大了研究等效深度的难度甚至会影响计算精度。相比之下，深度与陷波频率的关系式比较简化，可以更直接地研究等效深度的影响因素及其相应的变化规律。因此，笔者尝试从深度与陷波点频率的关系入手，研究等效深度的求取方法。

根据远场子波定义，接收远场子波的水听器距离震源十分远，而气枪沉放深度一般远小于这个距离，图1远场子波中直达波与震源虚反射的能量相差不大,因此，远场子波的表达式为式(6)。

sf(τ)=sd(τ)+Γsd(τ-Δτ)

(6)

其中：sd(τ)为直达波信号；sd(τ-Δτ)为震源虚反射。变换到频率域为：

sf(f)=sd(w)(1+Γe-i2πfΔτ)

(7)

其中：f为频率；而1+Γe-i2πfΔτ可视为直达波的滤波因子，或者称为虚反射滤波器设其为F(f)，其中Δτ=2h/vc，则可得式(8)。

(8)

其中：vc为海水中的声波速度；h为气枪阵列的陈放深度。当2πhf/vc=nπhn=(1,2,3...)时子波振幅为零，对应的频率为陷波频率。

图1展示了单枪子波的形成过程，同理立体震源子波也是下行直达波和鬼波叠加而成(图2)，而下行直达波由多个子阵的下行直达波同相叠加而成，上行直达波由子阵的鬼波非同相叠加而成(非同相叠加增大了陷波点的位置从而一定程度上抑制了陷波效应)。频率陷波法就是将该多枪合成子波视为单枪合成子波，利用其陷频点与陈放深度的关系，求取立体震源等效深度。

立体震源远场子波(由上行叠加波和鬼波叠加波组成)第一个正峰值和第一个负峰值之间的时间差为Δt，由此求得陷频为式(9)。

f陷波=1/Δt

(9)

结合式(1)、式(2)和式(9)可得式(10)。

h等效深度=v声速/2f陷波

(10)

3.2 立体震源脸谱分析

由图3可知，立体震源子波是由不同深度的震源子波叠加而成，陈放不同深度的相同能量子阵会产生不同形态的子波。同理，陈放同一深度的不同容量子阵产生子波的形态也不相同。通过比较图3中的子阵子波与立体枪阵子波的子波形态，立体震源子波a、b、c、d较子阵子波第一主峰值较大，第一负峰值偏小，初泡比很大，气泡效应减弱。而单纯分析子波形态，并不能有效分析出子波深度与其他参数关系。

图4为图3中各子波的功率谱。由图4可知，子阵陈放深度越深，其陷频点越小。根据褶积定理，各子阵功率谱相乘即为立体震源合成子波的功率谱，因此根据子波陷频点与深度之间的关系，可得到立体震源子波的等效深度。

图1 单枪远场子波形成过程Fig.1 The forming process of the single gun-far field wavelet(a)；单枪子波形成过程；(b)子波频繁谱分析结果

图2 立体枪阵子波形成过程Fig.2 The forming process of the stereo air gun source

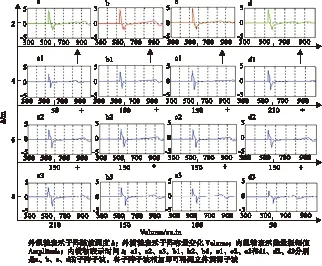
图3 立体震源子波脸谱Fig.3 Stereo source wavelet mask

故可知影响等效深度的主要因素是子波的陷频点，笔者通过研究影响陷波点的因素来，间接研究影响等效深度的因素。

3.3 立体震源陷波点的影响因素分析

3.3.1 内部因素

1)a子波容量。如图5(a)所示，子阵a1与a2的容量与深度值固定不变，a3深度值不变，容量成等比数列变化，而图5(b)中的b1、b2分别是频率陷波法和几何加权法求取的等效深度结果。由图5可知，随着深度8 m子阵容量的增大，几何加权法等效深度逐渐变大，而频率陷波法求取得等效深度值保持不变(约2.03 m),综上可知，频率陷波法等效深度与子阵容量大小无关；而频率陷波法求取得等效深度值一直保持不变(约2.03 m),由此说明，频率陷波法等效深度结果与子阵容量大小无关。

2)b子阵深度。如图6(a)所示，子阵a1和a2深度与容量皆不变，a3容量不变，深度成等差数列变化；图6(b)中b1和b2分别为频率陷波法和几何加权法求取得等效深度值，b2在2 m附近成陷频式上下变化，变化范围较小；b2保持递增趋势，变化范围相对较大。由此说明，陷频法等效深度值随子阵深度变化而变化。

图4 立体震源子波功率谱脸谱Fig.4 Stereo source wavelet power spectrum mask

图5 子阵容量影响因素分析Fig.5 Analysis of volume of sub-array(a)气枪在不同深度下不同容量变化曲线；(b)两种等效深度求取结果

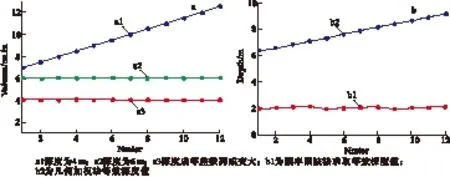
图6 子阵深度影响因素分析Fig.6 Analysis of depth of sub-array(a)子阵压强变化曲线；(b)等效深度结果

3)c子阵内部压强.由图7可知，无论是几何法还是陷频法，两种等效深度都不受子阵内部压强的影响。根据对气枪子波模拟的理论研究，a子阵容量、b子阵深度、c子阵压强为影响子阵性能的主要因素，然而通过对立体震源等效深度影响因素研究发现，影响立体震源等效深度的参数为子阵陈放深度，而子阵能量与子阵压强会影响立体震源子波能量，初泡比以及周期等参数，但无法影响立体震源合成子波陷波频率的位置，从而无法左右立体震源的等效深度。

3.3.2 环境因素

频率陷波法等效深度除了受子阵本身参数的影响之外，其对外部环境变化的敏感度也很高，然而，所有的外因都是通过内因起作用，据上面分析可知，所有能引起子阵深度变化的因素，都会间接的影响频率陷波等效深度。据此笔者给出了环境变量对陷频等效深度的影响分析。

1)a 海水反射系数。受海风，涌浪的影响，上行波的海面反射能量会受到影响，使海面反射系数小于等于“1”(图8)，海水反射系数的变化不会改变子波陷波频率，只会影响子波能量以及气泡周期，故等效深度不受海水反射系数影响。

2)b水听器方位。气枪阵列是利用不同容量气枪实现空间多方式组合，这使得无法将其看做点震源，其信号在水平和垂直方向上的变化很大。因此，水听器位于不同的方向，其接收子波的形态会存在一定差异。如图9所示，对称立体震源在不同方位角接收子波的频谱能量会随方位角变大而减弱。

笔者分别抽取距离立体震源垂直线成0°、30°、60°水听器接收的子波进行分析(图10)，位于不同方向的水听器接收子波的形态会有一定的差异，子波的陷频点随方位变化而变化，求取等效深度也随之变化。因此在实际子波分析时，要选择合适的方位尽量减小方位角误差。

图7 子阵压强影响因素分析Fig.7 Analysis of pressure of sub-array(a)子阵压强变化曲线；(b)等效深度结果

图8 不同海水反射系数R子波与其相应功率谱Fig.8 Different sub-sea wave reflection coefficient R and its corresponding power spectrum(a)子波；(b)功率谱

图9 立体阵列不同方位能量分布图Fig.9 Energy distribution of different azmuths(a)对称立体阵弄30 Hz能量平面图； (b)垂向横切面分布图(方位角90°频率0～50 Hz)能量轴为归一化振幅(DB)

图10 水听器不同方位接收子波与其相应功率谱Fig.10 Wavelet received by different orientations and its corresponding power spectrum(a)子波；(b)功率谱

4 应用效果

布置如图11所示，两侧子阵陈放5 m，中间子阵前部陈放6.5 m，后部陈放8 m，延时激发，各个深度对应的延时分别为5 m: 0 ms，6.5 m: 1 ms，8 m: 2 ms。垂直缆共有32道检波器。整个采集系统(震源+垂直缆)。垂直缆最深达400 m。记录的地震单炮数据的第1道对应沉放最深(400 m)的检波器，则第32道对应最浅的检波器。道间距6.25 m，从第1道至第32道的距离为193.75 m。

针对第26道检波点数据，将相邻10炮所记录的地震信号进行平均，压制随机噪音，获得远场子波(图12)。由图11可以看出，检波器所记录的子波对海面虚反射的压制效果较好。对第26道子波进行模拟，经过波形进行比较发现模拟结果与实测结果相差较大。实测子波有一个负起跳，且气泡脉冲相应对应效果较差；

综上可知，立体震源等效深度只与子阵陈放深度有关，子阵深度排布确立等效深度随之确立；然而在实际环境变化因素增多的情况下结果往往会有所误差，例如气泡在形成之后由于浮力的原因会上浮至海面，因此虚反射的效果会逐渐减弱。海风、涌浪等干扰因素致使海面不再是一个理想平面，会影响子波陈放深度的变化，使其求得结果远离真实。另外，数据实际采集过程中，由于水听器或记录仪器的物理属性，采样率与模拟数据存在差距，这些因素都会导致模拟数据与实际数据的差异。为消除这些外部差异笔者对模拟子波与实际子波同时做滤波，滤波参数为：6 Hz-20 Hz-200 Hz-400 Hz。

如图13所示，经过滤波之后，模拟子波与实际子波拟合效果良好(图13(a))，模拟子波与实际子波功率谱中的陷波点拟合效果良好(图13(b))，因此实际数据可以根据频率陷波法求取其等效深度值。

5 结论与建议

笔者研究了几何加权法和频率陷波法两种立体震源等效深度求取方法，并对其影响因素进行了分析，最后结合实际数据对频率陷波等效深度求取方法进行了完善，得到以下结论及建议：

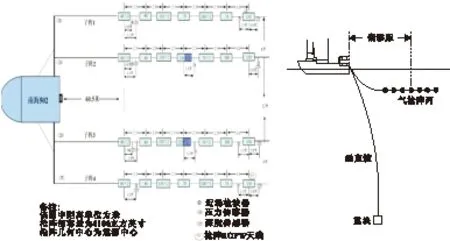
图11 南海502震源船阵列平面布置图和垂直缆布设图Fig.11 Vertical cable layout South China Sea 502 boat source array layout the unit of distance in graph is : m; the total volume of air gun array is:4100 cu.in(a)平面布置图；(b)垂直缆布设图

图12 第26道平均数据与模拟子波对比Fig.12 Section 26 average data and simulation sub-wave versus

1)几何加权法等效深度是基于几何角度求取的静态深度，其不会随外界环境变化而受到任何影响。

而频率陷波法是基于子波频谱特征原理，根据子波陷频特征获取深度信息，频率陷波法更具有依据性和可靠性。

2)在实际野外采集条件下，风浪、潮汐、船只等外界水环境的动态干扰会带来声波场的扰动，子波陷波点频率与理论数据会有所差异，陷频法能有效地反映环境变化，能更准确地反映等效深度。

3)立体震源子波相应参数研究能从整体角度出发研究立体震源相关机制，有助于更好的从整体角度压制虚反射，从而得到高分辨率的宽频带子波。

4)利用单枪子波参数关系式进行立体震源子波研究，可以在实际生产中提供便利，但也存在局限性，因此，建立一套能直接对立体震源子波进行研究的影响参数及其相关表达式是必要的。

图13 滤波后第26道平均数据与模拟子波对比Fig.13 The average actual wavelet of 26th trace and analog wavelet comparison(a) 为模拟子波与实际子波；(b) 分别为前两者的功率谱

[1] 陈浩林, 全海燕, 於国平,等. 气枪震源理论与技术综述(上)[J]. 物探设备, 2008, 18(4):211-217. CHEN H L,QUAN H Y,YU G P,et al.The theory of air gun and technology summary(volumeone)[J].Geophysical equipment,2008,18(4):211-217.(In Chinese)

[2] ZIOLKOWSKI A. A Method for Calculating the Output Pressure Waveform from an Air Gun[J]. Geophysical Journal of the Royal Astronomical Society, 1970, 21(2): 137-161.

[3] SCHULZE-GATTERMANN R. Physical aspects of the “airpulser” as a seismic energy source[J]. Geophysical Prospecting, 1972, 20: 155-192.

[4] SAFAR M H. The radiation of acoustic waves from an air-gun: Theory and experiment[J]. Geophysical Prospecting, 1976, 28:700-715.

[5] GILES B F, JOHNSTON R C. System approach to air gun array design[J]. Geophysical Prospecting, 1973, 21:77-101.

[6] NOOTEBOOM J J. Signature and amplitude of linear air gun arrays[J]. Geophysical Prospecting, 1978, 26: 194-201.

[7] BRANDSAETER H, FARESTVEIT A, URSIN B. A new high-resolution or deep penetration air gun array[J]. Geophysics, 1979, 44:865-879.

[8] JOHNSON D T. Understanding air-gun bubble behavior[J]. Geophysics, 1994, 59(11): 1729-1734.

[9] ZIOLKOWSKI A. Measurement of air-gun bubble oscillations[J]. Geophysics, 1998, 63(6):2009-2024.

[10]MACGILLIVRAY A O. An acoustic modeling study of seismic airgun survey noise in Queen Charlotte Basin: [D]. Victoria: University of Victoria, 2006.

[11]LI G F, CAO M Q, CHEN H L, et al. Modeling air gun signatures in marine seismic exploration considering multiple physical factors[J]. Applied Geophysics, 2010, 7(2): 158-165.

[12]王立明.范氏气体下气枪激发子波信号模拟研究: [D]. 西安: 长安大学, 2010. WANG L M. Simulation of sub-wave signal in gas Fan excitation: [D]. X′ian: Chang'an University, 2010.(In Chinese)

[13]MOLDOVEANU N. Vertical source array in marine seismic exploration[C]. 70th Annual International Meeting, SEG, Expanded Abstracts, 2000:53-56.

[14]PARKES G, HEGNA S. The principle of using complementary acquisition components to achieve broadband seismic[C]. 82nd Annual International Meeting, SEG, Expanded Abstracts, 2012: 1-5.

[15]EGAN M, GEORGE K, KASSEH E, et al. Full deghosting of OBC data with over/under source acquisition[C]. 77th Annual International Meeting, SEG, Expanded Abstracts, 2007:31-35.

[16]ABMA R, ZHANG Q, AROGUNMATI A, et al. An Overview of BP’s Marine Independent Simultaneous Source field trials[J]. 82nd Annual International Meeting, SEG, Expanded Abstracts, 2012: 1-5.

[17]HOPPERSTAD J, LAWS R, KRAGH E. Fundamental principles of isotropic marine source design[J]. 70th Annual International Conference and Exhibition, EAGE, Extended Abstracts, 2008:25.

[18]CAMBOIS G, LONG A, PARKES G, et al. Multi-level airgun array: a simple and effective way to enhance the low frequency content of marine seismic data[C]. SEG Technical Program Expanded Abstracts, 2009: 152-156.

[19]林松. 深水环境地震波激发技术研究[D]. 武汉: 中国地质大学, 2010. LIN L.Deep water seismic wave excitation technique[D]. Wuhan:Chinese Geology University,2010.(In Chinese)

The equivalent depth definition method of stereo air gun array

LIU Xueqin, LIU Huaisha, WEI Jia

(Key Lab of Submarine Geosciences and Prospecting Techniques, Ministry of Education,Ocean University of China,Qingdao 266100,China)

There is no evidence based on defining the equivalent depth of stereo air gun array. In order to have a comparison with the conventional air gun array, an optimal method for determining the equivalent depth of stereo air gun array is required. Based on the technology of air gun simulation under practical conditions. This paper gives some representative simulations of stereo air gun array and proposed two equivalent depth definition methods: geometric weighting equivalent depth method(GWEDM) and notch frequency equivalent depth method(NFEDM). In addition, the influence factors affecting the NFEDM is found, such as: the depth of air gun sub-array and the direction of hydrophone. By a detailed analysis of actual data, a effective equivalent depth definition method in practical production is present.

stereo air gun array; GWEDM; NFEDM; equivalent depth

2016-02-26 改回日期：2016-04-11

国家自然科学基金(41176077，41230318，41204088);国家863 项目(2013AA092501);国土资源部海洋油气资源与环境地质重点实验室开放基金(MRE201303)

刘雪芹(1989-)，女，博士，主要从事地震勘探资料处理与解释方法研究工作，E-mail：1226535203@qq.com。

刘怀山(1962-)，男，教授，主要从事海洋探测数据的采集与处理工作，E-mail：lhs@ouc.edu.cn。

1001-1749(2017)01-0081-09

P 631.4

A

10.3969/j.issn.1001-1749.2017.01.12