例析极限思想在高中数学解题中的应用
汪仁林
陕西省咸阳市乾县杨汉中学 (713300)
例析极限思想在高中数学解题中的应用
汪仁林
陕西省咸阳市乾县杨汉中学 (713300)
极限思想是高中数学中重要的数学思想,它使人们能够从有限认识无限,从近似认识精确,从量变认识质变.虽然目前高中教材没有给出极限的严格定义,但无论是教材内容还是习题解答都大量地应用着极限思想.极限作为一种运算在高中数学中的要求较低,一般只要理解即可,然而高中学习极限思想一方面能锻炼学生的思维能力,提高解题水平,另一方面为以后高等数学的学习做铺垫.本文对极限思想在高中数学解题中的应用作些探讨.
1.教学中如何引导学生掌握简单的极限运算

①若x→a时,f(x)→0且g(x)→0,则

②若x→a时,f(x)→∞且g(x)→∞,则




2.极限思想应用实例剖析

(1)求点M轨迹C的方程;
(2)若过点D(2,0)的直线l与(1 )中的轨迹C交于不同的两点E,F(E在D,F之间),试求ΔODE与ΔODF面积之比的取值范围(O为坐标原点).

图1
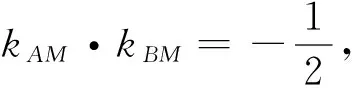


评析:此题第(2)问一般思路是:设直线方程,将面积之比转化为E,F两点纵坐标之比或横坐标的表达式,将直线方程与椭圆方程联立,利用韦达定理和“设而不求”的思想,最终转化为函数求值域,运算量很大,看似简单,容易入手,学生最终完成需要较强的观察能力、化归转化思想且对学生的运算能力有较高的要求.比较可知,用极限思想非常简便,其实这种思路的获得途径也是很直接的,将比值的范围转化为分别求分子分母的最值,用极限思想求解.说明在平时做题时不能仅凭经验,只要认真审题,把未知问题化归转化为我们熟悉的问题,从多角度思考,就能少走弯路,起到事半功倍的效果!

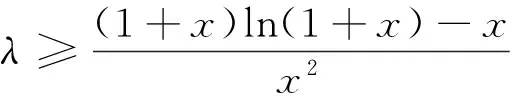
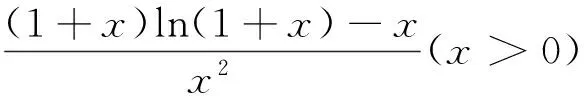
因为φ′(x)=


评析:对比考题标准答案可知,此种解法的优越感不言而喻.考题标准解答技巧性强,略显突兀,学生普遍反映能看懂但想不到,而且将问题转化为含参数的函数求最值,分类目标不明确,较难处理. 本解法的优点是:分类讨论目标非常明确,思路清晰;将问题转化为不含参数的函数求最值,非常方便;通过分离参数、构造函数、二次求导,再借助洛比达法则使问题轻松获解,容易理解和掌握. 可操作性强,深受学生青睐!
通过以上的分析,我们能够感受到极限思想对有些问题的解决是不可或缺的.同时,极限思想的合理且有效应用也能反映出学生在个性化处理中的不同理解,以及他们所反映出来的不同层次、不同深度的理性思维水平.所以中学数学教学应该在培养极限思想、掌握极限方法等方面做一些研究,这样就更有利于高校选拔,更有利于学生的成长并影响着其未来的发展.
[1]赵文涛,汪仁林.洛比达法则该不该教?——对一道高考题的困惑[J].中学数学研究(江西),2014(06).
*本文是陕西省教育科学规划课题《高中生数学“懂而不会”的成因和对策研究》(课题批准号:XDKT3071)阶段研究成果.

