星载大功率复杂微波部件微放电效应数值模拟

李韵，崔万照，张洪太，殷新社，王洪广，张剑锋，贺永宁

1.西安交通大学 电子信息工程学院, 西安 710049 2.中国空间技术研究院 西安分院 空间微波技术重点实验室, 西安 710100 3.东南大学 毫米波国家重点实验室,南京 210096

星载大功率复杂微波部件微放电效应数值模拟

李韵1,2，崔万照2，*，张洪太2，殷新社2，王洪广1，张剑锋3，贺永宁1

1.西安交通大学 电子信息工程学院, 西安 710049 2.中国空间技术研究院 西安分院 空间微波技术重点实验室, 西安 710100 3.东南大学 毫米波国家重点实验室,南京 210096

随着航天器有效载荷技术向高功率、小型化持续发展，复杂结构微波部件微放电数值模拟与阈值分析成为影响微放电分析的基础瓶颈问题。基于电磁时域有限差分计算方法与粒子模拟技术，结合二次电子发射模拟，提出了微放电电磁粒子联合仿真方法，数值模型中考虑了真实电子间的库仑力以及电子运动产生的电荷和电流变化对电磁场的影响，解决了复杂结构微波部件微放电三维数值模拟技术难题。实现了在统一的三维空间网格与时间步进行电磁场值演变计算、电子运动状态变化推进计算与二次电子产额与能量分布计算，基于得到的二次电子数目随时间变化趋势实现了微放电阈值预判，通过微放电电子随时间演化获得了微放电过程具体物理图像及放电位置，并与实际器件微放电实验进行了对比验证。结果表明，所提出的三维电磁粒子数值模拟方法可对大功率微波部件微放电效应的物理过程与具体放电位置进行三维描述，预测的阈值与微放电实验测量值吻合良好，误差小于1.2 dB，验证了该方法的有效性与准确性，对于深入研究微放电效应微观物理机制、提高大功率微波部件微放电设计与分析水平具有重要意义。

空间；大功率；微放电；数值模拟；无源器件

随着航天器有效载荷技术的发展，系统工作功率越来越大，使得空间发生微放电的可能性大大增加，微放电效应成为影响空间大功率微波部件可靠性的基础性关键问题[1-5]，国内外针对大功率微波部件进行的微放电研究也日趋活跃，主要研究机构有欧洲航天局(ESA)、瑞士Chalmers理工大学、西班牙Valencia大学、俄罗斯科学院应用物理所(IAP)、通用物理所(IGP)和美国Michigan大学。传统的微放电阈值预测往往依赖于平行平板近似和蒙特卡洛运动模型[4-6]。基于平行平板近似的微放电敏感曲线由ESA提出[6]，是空间工业中常用的微放电余量设计的标准方法。由该曲线得到的预测结果对于平板无谐振结构而言是可信的。但当微波部件结构更为复杂，尤其是存在谐振时，使用该曲线进行微放电设计存在较大误差。

空间大功率微波部件微放电效应三维数值模拟方法相比较于基于平行平板近似与蒙特卡洛运动模型的解析数值模拟方法，具有直观分析微放电完整物理过程、可采集微放电效应电子运动物理图像进行放电区域分析以及微放电阈值功率预测精度更高等优势，但微放电效应基础机理的复杂性以及空间自由电子运动的随机性导致要建立数值模型难度巨大，该方面研究在长期以来几乎近于空白。目前，空间大功率微波部件的微放电分析主要基于解析方法[7-11]，微放电阈值功率主要通过进行反复实验确定，实验周期长，研制经费高。

作为一种基于第一性原理的数值计算方法，粒子模拟(Particle In Cell, PIC)技术常用于等离子体物理中的电子轨迹追踪[12-15]。结合电磁计算理论与二次电子发射理论，可利用PIC技术对微放电效应初始化及形成过程中电子运动状态的演变进行追踪，探讨空间大功率微波部件微放电效应的三维数值模拟方法。但是在公开的文献中鲜少有该方面的文献报道[14,16]。

本文提出以自由电子作为研究对象，进行空间大功率微波部件微放电效应的三维电磁粒子数值模拟方法研究，旨在填补空间大功率微波部件微放电效应三维数值模拟这一技术空白。相比较于现有的微放电数值模拟方法，如ESA提出的基于平行平板近似与蒙特卡洛运动模型的微放电敏感曲线而言，本方法对微放电形成过程的微观物理机理以及实际微波部件的电磁场分布计算所做近似更少，基于第一性原理进行迭代运算模拟了电子的真实运动状态，更符合物理实际。同时，对于特定金属材料的二次电子发射特性模型采取了开源设计，可在进一步的研究中加入拟合具体加工工艺下具有特定表面形貌的金属材料的二次电子发射特性理论模型，从而提高实际空间大功率微波部件微放电设计余量精确度，具有应用意义。

1 微放电三维电磁粒子数值模拟 方法

微放电效应是一种复杂的非线性作用过程，源自于由金属材料的二次电子发射导致的二次电子谐振倍增。由于微波部件实际电磁场分布的复杂性，完全采用解析方法研究微放电效应对物理实际近似较多，误差较大。为了实现对大功率微波部件微放电效应初始化及形成过程的数值模拟，选取自由电子作为研究对象，通过建立电子初始化分布、电子与电磁场耦合作用以及二次电子发射等物理过程的算法模型，基于第一性原理模拟完整的微放电过程，最终根据电子数目及运动状态的变化预测微放电阈值。基于第一性原理，只要定义了电子与场的初始条件，并给出电子运动与电磁场演变的基本物理规律(例如麦克斯韦方程与洛伦兹运动方程)的合适表达，电子将保持运动直到满足运算结束的条件或者总的计算时间结束。特定结构中的电磁场分布通过时域有限差分方法(Finite Difference Time Domain Method, FDTD)在离散网格中求解麦克斯韦差分方程得到[17-19]。同时，电子运动的演变通过在时域求解相对洛伦兹运动方程的差分形式得到。由电子运动产生的电荷和电流被插值加入离散网格各节点上的麦克斯韦方程的源项，通过在每一个时间步重新计算更新电磁场量，计入空间电荷效应，模拟电子与电磁场耦合作用的实际物理过程。

1.1 电子与场的初始化

作为整个数值模拟的基础，首先建立微波部件的三维模型和模拟真空工作环境的微放电数值模拟区域，根据工作频率与微波部件微小结构将三维模型与数值模拟区域剖分成多个直六面体网格。粒子模拟方法采用宏粒子或粒子云模型[20]代表体积约为德拜球大小的空间内的实际电子，是目前国际上在航天器微波部件与空间电子相互作用研究领域先进的数值模拟方法，对于揭示复杂的物理过程、发现新的物理规律有着非常重要的作用。采用宏粒子(粒子)作为初始电子与二次电子的三维模型，粒子的体积忽略不计，电量及质量由包含的电子数目N决定，为N倍电子电量和质量。

对电子在微波部件内真空区域自由运动的物理实际进行模拟，提出初始粒子空间分布模型。在数值模拟初始设置阶段，将粒子随机分布在所建立的微放电数值模拟区域中。为保证模拟结果的准确性，初始粒子空间分布密度不宜过低。初始粒子的动力学能量的取值范围设置为0～10 eV较为符合物理实际，发射相位的取值范围为0°～180°(0°表示垂直于微波部件的金属表面)。固定网格节点上的电磁场值初始设置为零。在电磁波传输进入微波部件的端口处的网格中定义载波信号，激励起一定工作模式的电磁场，并在微波部件中传输。

1.2 电子与场耦合作用的三维自洽理论模型

在直六面体网格中建立电子与场耦合作用的三维自洽理论模型，电磁场值在直六面体网格中的空间与时间分布格式采用Yee网格形式。基于Yee网格[17]求解时域离散的Maxwell方程组，可得到网格节点上电磁场值随时间与空间演变的数值解。在模拟的起始阶段，电子随机分布在Yee网格中，在电磁场力的驱动下运动，电子动力学(主要参数为运动速度v与运动位移r)满足相对洛伦兹力方程。为了在网格中同时推进电磁场演变与粒子运动，将Maxwell方程在nΔt时刻、(iΔx,jΔy,kΔz)位置处进行离散，将相对洛伦兹力方程同样在nΔt时刻离散，离散形式为

(1)

(2)

式中：E，B为电场强度和磁感应强度；n为第n个时间步；q为电子电量；m为电子质量；Δt为时间步长；Δx,Δy,Δz分别为x,y,z方向的空间离散步长。

如图1所示，粒子p处的电磁场值通过对网格节点上的电磁场值进行插值得到。

Vicente等人提出的矩形波导结构微波部件微放电数值分析方法[21]与Semenov等人提出的同轴线微放电数值模拟方法[7]均不考虑电磁场与电子的耦合作用，在得到微波部件电磁场分布后推进电子运动进行微放电数值模拟。然而，粒子在微波部件内部真空环境中真实运动时，粒子与粒子之间存在库仑斥力，粒子运动在空间中引起电荷变化和电流变化。将电磁场对粒子的作用力以及粒子运动对电磁场分布产生的影响定义为电磁粒子自洽作用，在相同的网格中耦合了Maxwell方程与相对洛伦兹力方程的基础上，将粒子运动产生的电荷与电流变化插值到粒子所在网格的网格节点上，更新Maxwell方程源项，在网格中建立粒子与电磁场耦合作用的三维自洽理论模型。

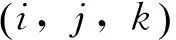
(3)

式中：l=1,2，分别表示起点和终点处电荷对于网格节点处电磁场分布产生的电荷变化量。根据电流连续性方程

(4)

可得到各网格线上产生的电流变化量。如图2所示，x1,x2,x3分别表示与网格节点相邻的3条网格线方向的分量，以与ΔQ(i,j,k)相邻的三条网格线上的电流变化量为例，分别为

(5)

式中：

(6)

电子间的库仑斥力通过电子带电量的大小体现，电荷线性插值分配计入了电子所带电荷对空间电磁场分布产生的影响，间接计入电子间的互作用力。

1.3 二次电子发射模型

当电子与金属碰撞时，若碰撞能量与角度满足一定条件，将从金属中激发出二次电子。早期的微放电理论研究中，采用二次电子发射模型可对相应金属材料的二次电子发射特性进行描述，并基于实验数据推导了二次电子发射特性经验公式[4]。

在微放电效应形成过程中，电子由电磁场力驱动在微波部件内部的真空环境中运动，最终与微波部件金属表面发生碰撞。每次撞击产生的二次电子的运动状态随时间变化的趋势决定了是否发生微放电电子雪崩效应。本数值模拟方法采用经验公式[4]描述金属材料的二次电子发射特性(SecondaryEmissionYield,SEY)，模拟微放电效应建立过程中电子与金属材料作用的物理过程。同时，对金属材料的二次电子发射模型采取开源设计，考虑在进一步的研究中加入拟合具体加工工艺下具有特定表面形貌的金属材料的二次电子发射特性理论模型，提高实际微波部件微放电设计中阈值的数值模拟精度。对于Vaughan模型而言，取决于碰撞能量Ei=mv2/2与碰撞角度θ(0°代表垂直碰撞)，二次电子发射系数δ通过Vaughan提出的经验公式计算得到：

(7)

(8)

式中：w=Ei/Emax,当w<1时k=0.62，当w>1时k=0.25；ks为金属材料的表面粗糙度；δmax0和Emax0为由金属材料决定的垂直入射情况下的二次电子发射参数。采用Vaughan模型，对于典型金属银而言，当电子垂直入射时(θ=0°)，其二次电子发射系数曲线如图3所示，其中二次电子发射系数是入射能量的函数。

1.4 微放电阈值功率

经过一定时间步的迭代计算，记录一定输入功率水平下粒子数目随时间的变化趋势。若微放电效应得以建立，则粒子在金属表面之间来回反复碰撞且每次碰撞后平均出射的电子总数总是大于入射电子总数，发生微放电电子雪崩效应，粒子在金属表面之间以相对谐振的形式运动，其数目呈指数增长[4]。若未能建立起微放电效应，则粒子数目随着数值模拟时间步的推进将逐渐减少。因此，本数值模拟方法中将导致粒子相对稳态，即粒子数目在一定时间内围绕一定数值上下波动的输入功率，定义为微放电阈值功率。该三维数值模拟方法提供了微波部件中微放电效应初始化及形成过程的直观物理图像，通过观察微放电效应建立以后粒子的空间分布可预测放电位置。

由于微波部件的输入功率可以通过改变输入载波信号加以改变，通过对不同功率水平下电子数目随时间的演变趋势进行比较，预测微放电放电阈值功率。

2 数值模拟方法的有效性与结果 讨论

2.1 数值模拟结果与讨论

采用典型微波部件——5阶矩形波导阻抗变换器验证所讨论的大功率微波部件微放电效应数值模拟方法。为便于加工，采用5阶波导变换器的对称结构作为研究对象，工作中心频率f为3.85 GHz，金属材料为银，银的二次电子发射特性如图3所示，采用标准WR229波导作为输入输出波导端口，波导变换器的横向尺寸为58.17 mm，每一阶的纵向尺寸分别为29.08 mm,19 mm,12 mm,3 mm,1 mm，电磁波传输的主模为TE10模，每个粒子包含的电子数为100。

对大功率空间微波部件微放电效应进行数值模拟，主要包括空间中自由电子分布建模、微波部件实际电磁场分布计算、电子运动动力学建模、电子与电磁场自洽作用建模、电子与金属材料表面碰撞时二次电子发射特性建模以及微放电阈值功率预测。对于波导阻抗变换器而言，在电子与场的初始化阶段，粒子在空间网格中随机分布，每3个网格选择1个网格设置粒子，粒子在网格中的位置随机，粒子的动力学能量设定为5 eV，发射相位在0°～180°之间随机选择，电磁场初始值为零，输入载波信号为幅度为A0、频率为3.85 GHz、相位为0的时域余弦信号。

采用电磁粒子三维自洽理论模型模拟粒子与电磁场的自洽耦合作用，在每个时间步内迭代更新电磁场值与粒子运动参数，随时间步推进电磁场演变与粒子运动。当粒子与阻抗变换器的金属表面发生碰撞时，根据粒子碰撞能量与速度方向，采用二次电子发射模型，得到二次粒子产额以及二次粒子能量与相位分布。

改变输入功率，即改变相应的输入载波信号幅度A0进行多次微放电效应数值模拟，记录粒子数目随时间的变化趋势如图4所示。当输入功率低于1 450 W时，经历数个周期的相位选择后，粒子数目将持续衰减，不能建立起微放电效应。与此相反，当输入功率足够大时，粒子数目呈指数增长，将发生电子雪崩效应，最终导致微波部件中的微放电击穿。而当输入功率为1 450 W左右时，粒子数目随时间在一定数量范围内波动变化，达到相对平衡状态。因此，预测该阻抗变换器的微放电阈值功率为1 450 W。

Vaughan与Hatch等在早期的微放电理论研究中指出，要最终导致微放电效应，只有当发射二次电子时电磁场相位在一定范围内，二次电子能够通过金属表面之间的间距，并获得加速，以较高能量与金属表面碰撞并再次撞击出二次电子，且二次电子平均产额大于1，导致电子数目随时间变化越来越多，引发电子雪崩效应[4-5]。通过三维数值模拟，当输入功率高于1 450 W的放电阈值，设置为1 700 W时，可以观察到，初始粒子在阻抗变换器内部真空环境中均匀随机分布，随着数值模拟时间步的推进，部分区域处粒子逐渐减少，仅在阻抗变换器最窄间隙处中间位置(图5中红色区域)出现区域性粒子聚集现象，其物理图像如图5所示，并随着时间步的继续推进粒子数目逐渐增加，呈指数增长，在金属缝隙间以类似谐振的形式运动，验证了微放电形成过程中的相位聚焦效应与微放电效应建立以后的二次电子谐振倍增。

2.2 实验验证

进一步对微放电阈值功率预测的有效性与准确度进行验证。如图6所示是阻抗变换器的拓扑图。阻抗变换器经加工后涂覆银在真空腔中进行微放电实验，实验持续半小时以上，实验结束后观察到在阻抗变换段最窄间距处出现淡黄色痕迹，为电子不断撞击所致。将采用三维自洽数值模拟方法预测的阈值与实验得到的阈值进行比较，结果如表1所示。预测结果与实验结果吻合良好，有效验证了本数值模拟方法。进一步，采用三维自洽数值模拟方法对可能发生放电的位置进行了预测，即图5中红色区域，在微放电实验中同样得到了验证。

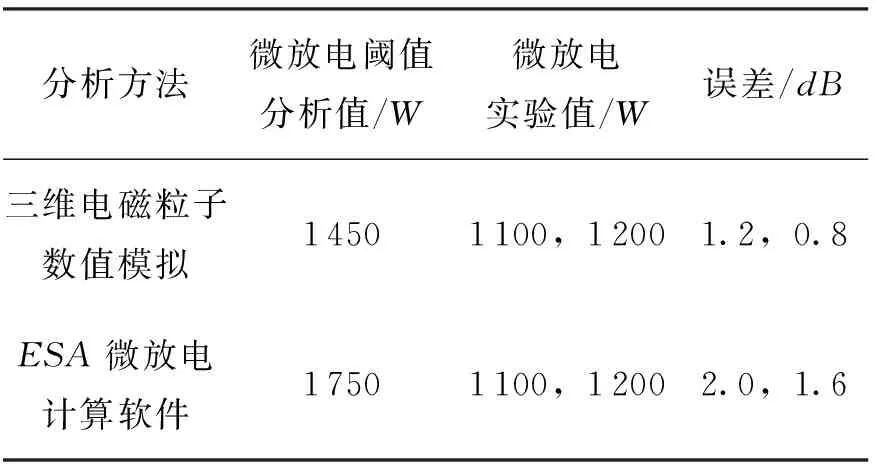
表1 阻抗变换器的微放电阈值

3 结束语

针对空间大功率微波部件的高微放电风险，本文克服了传统近似分析方法无法模拟微放电物理过程、阈值预测精度有限的技术难题，提出了一种实际微波部件微放电三维电磁粒子数值模拟与微放电阈值功率预测方法。结合时域有限差分电磁计算方法与粒子模拟技术，推导了微放电电子在电磁场作用下运动并与电磁场耦合作用的三维自洽理论模型，对微放电形成过程中的电子运动学进行模拟，模拟了微放电初始及形成过程中电子运动状态随时间的变化，基于第一性原理进行时域迭代数值计算，最终实现微波部件微放电效应三维模拟。采用5阶波导阻抗变换器的对称结构作为研究对象，进行微放电三维数值模拟以及微放电实验，获得微放电阈值功率预测值与实验值。数值模拟记录了所有二次电子运动状态随时间的变化趋势，三维显示了微放电效应形成过程的物理图像，为微放电微观机理研究提供了有效依据。结果表明，要在微波部件中激发起微放电效应，根据微波部件物理结构的不同，电磁场必须满足一定的相位、频率条件，输入功率必须高于一定的阈值功率，即满足微放电效应初始化条件。而在微放电形成过程中，可观察到电子经历二次电子发射、相位选择、相位聚焦、二次电子谐振倍增等物理过程，在微波部件金属表面的局部区域引发放电现象。预测的阈值与由数值模拟获得的微放电阈值功率预测值与实验值吻合良好，验证了该方法的有效性与准确性，对于深入研究空间大功率微波部件微放电效应微观机理，提高国内空间工业微放电设计水平具有重要意义。后续工作将围绕二次电子发射数值模型准确建模与算法持续改进展开。

References)

[1] 乌江，白婧婧，沈宾，等. 航天器抗内带电介质改性方法[J].中国空间科学技术，2010, 30(2): 49-54.

WU J, BAI J J, SHEN B, et al. Formation mechanism of anti-deep-charged modification for space dielectric[J]. Chinese Space Science and Technology, 2010, 30(2): 49-54(in Chinese).

[2] IGLESIAS D G, PÉREZ A M, ANZA S, et al. Multipactor in a coaxial line under the presence of an axial DC magnetic field[J]. IEEE Electron Device Letters, 2012, 33(5):727-729.

[3] CHANG C, ZHU M, VERBONCOEUR J,et al. Enhanced window breakdown dynamics in a nanosecond microwave tail pulse[J]. Appl.Phys.Lett., 2014, 104:253504.

[4] VAUGHAN J R M. Multipactor[J]. IEEE Trans. Electron Devices,1988, ED-35: 1172.

[5] HATCH A, WILLIAMS H. The secondary electron resonance mechanism of low-pressure high-frequency gas breakdown[J]. IEEE Journal of Applied Physics., 1954, 25: 417-423.

[6] ESA-ESTEC. Space engineering: multipacting design and test, ECSS-20-01A[R].The Netherlands:ESA Publication Division, 2003.

[7] SEMENOV V E, ZhAROVA N, UDILJAK R. Multipactor in a coaxial transmission line II Particle-in-cell simulations[J]. Physics of Plasmas,2007, 14: 033509.

[8] RASCH J, SEMENOV V E, RAKOVA E, et al. Simulations of multipactor breakdown between two cylinders[J]. IEEE Transactions on Plasma Science, 2011, 39(9):1786-1794.

[9] SAZONTOV A, ANDERSON D, VDOCICHEVA N, et al.Simulations of multipactor zones taking into account realistic properties of secondary emission[C]//Proceeding of 4th International Workshop on MULCOPIM, 2003.

[10] AVIVIERE T, ANTONIO P, MING Y, et al. Multipactor breakdown simulation code[C]//Proceeding of 7th International Workshop on MULCOPIM, 2011.

[11] CHANG C, HUANG H J, LIU G Z, et al. The effect of grooved surface on dielectric multipactor[J]. Journal of Applied Physics, 2009, 105:123305.

[12] HOCKNEY R W, EASTWOOD J W. Computer simulation using particles[M]. New York: McGraw-Hill, 1981.

[13] EASTWOOD J W. The virtual particle electromagnetic particle-in-cell method[J]. Computer Physics Communications, 1991, 64: 252-266.

[14] GOPLEN B, LUDEKING L, SMITHE D, et al. User configurable MAGIC for electromagnetic PIC calculations[J]. Computer Physics Communications,1995, 87:54-86.

[15] LEMKE R W, GENONI T C, SPENCER T A. Three-dimensional particle-in-cell simulation study of a relativistic magnetron[J]. Physics of Plasmas, 1999, 6:603-613.

[15] LI Y,CUI W Z,WANG H G, Simulation investigation of multipactor in metal components for space application with an improved secondary emission model[J]. Physics of Plasma,2015，22:053108.

[16] YEE K S. Numerical solution of initial boundary value

problems involving Maxwell′s equations in isotropic media[J]. IEEE Transaction on Antennas and Propagation, 1966, AP-14:302-307.

[17] TAFLOVE A, HAGNESS S C. Computational electrodynamics: the finite-difference time-domain method[M]. 2nd ed. Norwood: Artech House, 2000.

[18] YOU J W,WANG H G,ZHANG J F.Highly efficient and adaptive numerical scheme to analyze multipactor in waveguide devices[J]. IEEE Transactions on Electron Devices,2014(10).

[19] HOCKNEY R W, EASTWOOD J W. Computer simulation using particles[M]. New York: McGraw-Hill, 1981.

[20] VICENTE C, MATTES M, WOLK D, et al. Multipactor breakdown prediction in rectangular waveguide based components[C]//Proc.IEEE MTT-S Int. Microw.Symp.Dig., 2005: 1055-1058.

(编辑：高珍)

A novel simulation method of multipactor in complex component for satellite application

LI Yun1,2，CUI Wanzhao2,*,ZHANG Hongtai2，YIN Xinshe2，WANG Hongguang1，ZHANG Jianfeng3，HE Yongning1

1.KeyLaboratoryofPhysicalElectronicsandDevicesoftheMinistryofEducation,Xi′anJiaotongUniversity,Xi′an710049,China2.ScienceandTechnologyonSpaceMicrowaveLaboratory,ChinaAcademyofSpaceTechnology(Xi′an)Xi′an710100,China3.StateKeyLaboratoryofMillimeterWaves,SoutheastUniversity,Nanjing210096,China

With the development of high power and miniaturization in satellite payload, accurate simulation and threshold analysis for multipactor incomplex component becomes bottleneck problem. Based on the particle-in-cell technology and the secondary electron emission theory, a three-dimensional simulation method for multipactor was presented. The numerical algorithm was self-consistent since the interaction between electromagnetic fields and particles was properly modeled. The generation of multipactor is visualized,so that a deep insight into the physical mechanisms of this effect was gained. In order to validate the method, multipaction in the impedance transformer was studied. By analyzing the evolution of the electron numbers obtained by our method, multipactor thresholds of these components were estimated and the most sensitive positions where multipactor occurs were visualized.The results show good agreement with the experimental results and the simulation error is less than 1.2 dB.

space；high power；multipactor；numerical simulation；passive component

10.16708/j.cnki.1000-758X.2017.0040

2016-08-31；

2017-01-17；录用日期：2017-03-17；

时间：2017-03-21 15:37:13

http://kns.cnki.net/kcms/detail/11.1859.V.20170321.1537.006.html

国家自然科学重点基金(U1537211)；空间微波技术重点实验室基金重点项目(9140C530101150C53011)

李韵(1986-)，女，博士研究生，genliyun@126.com，研究方向为空间微波大功率特殊效应

*通讯作者：崔万照(1975-)，男，研究员，cuiwanzhao@126.com,研究方向为空间大功率微波技术

李韵，崔万照，张洪太，等.星载大功率复杂微波部件微放电效应数值模拟[J].中国空间科学技术, 2017,37(2)：3-80.LIY,CUIWZ,ZHANGHT,etal.Anovelsimulationmethodofmultipactorincomplexcomponentforsatelliteapplication[J].ChineseSpaceScienceandTechnology, 2017,37(2)：73-80(inChinese).

V419+.2

A

http://zgkj.cast.cn