电子束撞击介质表面引发的带电现象分析

王丹，贺永宁,*，李韵,2

1.西安交通大学 电子与信息工程学院，西安 710049 2.中国空间技术研究院 西安分院 空间微波技术重点实验室，西安 710100

电子束撞击介质表面引发的带电现象分析

王丹1，贺永宁1,*，李韵1,2

1.西安交通大学 电子与信息工程学院，西安 710049 2.中国空间技术研究院 西安分院 空间微波技术重点实验室，西安 710100

现有关于介质微波部件微放电的相关研究多从谐振条件及出射电子产额方面出发分析微放电发生原因及其抑制方法，而很少分析航天器表面电位对于微放电发生的影响。文章对碰撞电子与介质表面相互作用后二次电子发射特性进行综合分析；重点研究了不同介质表面初始电位情况下，恒定能量的电子束流持续轰击介质表面时介质表面电位及电子束流碰撞能量的变化趋势；并对稳定后的电子束流碰撞能量和介质表面电位进行了理论计算,计算结果表明系统平衡状态时的表面电位受初始电子能量及第二临界能量影响有明显改变。此外，文章探究了单一能量及连续能量入射介质表面时表面带电对于二次电子发射的影响，研究表明：带有电位φ的表面会使临界能量发生偏移量为-eφ的相对偏移；对于连续能量的入射电子束，介质表面带电会很大程度上改变入射电子束的能量范围，从而影响微放电发生的风险。

航天器表面带电；二次电子发射；碰撞能量；表面电位；微放电

微放电效应，即二次电子倍增效应是真空环境中工作的大功率微波部件性能退化或失效的一个重要机制，受到了航天微波设备、高能粒子加速器及真空电子器件领域广泛的关注[1-5]。微放电效应是指微波部件在1×10-3Pa或更低压强条件下，传输大功率微波信号时发生的谐振放电现象[5-7]。其主要发生机理是：电子在微波部件传输的射频电场中被加速而获得能量，获得能量的电子在撞击材料表面时，如果同时满足谐振条件[8]和二次电子产额大于1，就会产生二次电子倍增现象[9]。依据微放电发生时电子运动轨迹与结构几何边界的关系，划分为双边微放电和单边微放电[10]。大功率微波器件内发生的微放电是双边微放电的典型例子，而高功率微波源射频窗口介质表面发生微放电则是单边微放电的典型例子。

随着中国航天技术的快速发展，导航卫星、通信卫星、遥感卫星等卫星电子系统中微波器件越来越朝着大功率、小型化方向发展，微波开关、输出滤波器、输出多工器、开关矩阵、天线馈源等易于发生微放电[11]，一旦发生微放电问题，轻则引起通信系统噪声电平抬高，输出功率下降，进而损坏微波部件表面，缩短微波部件寿命；重则造成微波传输系统驻波比增大，信道阻塞，导致微波部件永久性失效，甚至某个通信信道或者整个微波传输系统彻底失效，因此提高大功率微波器件的微放电阈值尤为重要[12]。

国外针对抑制微放电效应的需求始于20世纪中期，包括开展空间大功率微波部件微放电效应的理论分析、模拟仿真、抗微放电部件设计等方面的研究[10]。关于微放电的仿真工作，欧洲航天局已经开发出了基于时域有限差分法和粒子轨迹追踪的仿真模块的仿真软件。Sazontov等结合仿真和试验，研究了微放电敏感区域与二次电子发射系数峰值(δmax)及初始电子速率分布的依赖关系，该研究表明较大的δmax会导致微放电敏感区域交叠，且随着速率增加，该区域会进一步扩大交叠[13]。此外，还有部分关于微放电效应的研究工作探索了通过破坏谐振条件[14]或抑制二次电子产额[15]而达到抑制微放电的目的。

对于介质填充的大功率微波器件，所填充介质的表面存在发生单边微放电的风险[16-19]，满足谐振频率和二次电子产额大于1是导致介质单边微放电的根本原因[20-21]。因此，从微观层面分析电子与介质的相互作用过程有助于从根本上提高大功率微波器件的微放电阈值。本文通过综合分析单能电子束入射情况下介质表面带电行为，详细研究了在不同条件下的介质表面充放电过程及该系统的最终平衡状态，并阐释了介质表面带电对电子倍增现象是否发生的影响规律。本文工作对从介质表面带电出发研究微放电效应提供了理论基础，对今后探索新的介质表面微放电抑制方法具有一定的理论指导价值。

1 介质表面二次电子发射特性分析

电子束与介质表面作用时，需要考虑诸多因素的影响，如电子束能量、介质表面电势、环境因素等。本节讨论中忽略环境因素的影响，在只考虑入射电子束能量及介质表面初始电势的情况下，探究电子束与介质表面持续作用时，出射电子通量与入射电子通量之间的关系。在此过程中考虑能量恒定的电子束流持续轰击介质表面，并假定电子束是平行的且不会产生能量的扩散。设初始电子的能量为Ep，碰撞时电子能量为Ei，介质表面初始电位为φi，e为元电荷，对于电子，其电荷量为-e。电子与介质表面相互作用时，以上几个参数存在如下关系：

(1)

式(1)表明了电子束的碰撞能量与初始能量及介质表面初始电位的关系。电子与介质表面相互作用后，会有3种情况：出射背散射电子、出射二次电子、被材料表面吸收，具体示意如图1所示。

设δ和η分别为二次电子发射系数和背散射电子发射系数，则介质表面总二次电子产额(TotalsecondaryElectronYield,TEY)可以表示为δ+η。在数学中，对电子速度v积分可得到电流密度(即电子通量)，在该物理过程中，初始电子通量Jin可描述如下：

(2)

式中：f(v)为粒子的速度分布公式，处于平衡状态时，等离子体速度服从麦克斯韦分布：

(3)

式中：n为粒子密度；m为粒子质量；k为玻尔兹曼常数；T为空间中环境温度。实际测试中，容易测得电子能量E而非电子速度v，因此可以通过表达式：

(4)

使用能量代换速度，则关于粒子速度的麦克斯韦分布方程可以表示如下：

(5)

能量代换后的入射电流密度表达式可表达如下：

(6)

对于出射电流，考虑二次电子流和背散射电子流，设δ(E)和η(E)分别为二次电子系数和背散射电子系数关于电子入射能量的函数，则二次电子通量Jse和背散射电子通量Jel可分别表示为：

(7)

(8)

忽略光电流、环境束流等微小影响，总的出射电子通量为：

(9)

若令电子的入射通量和出射通量相等，即可得到电流平衡方程：

(10)

带入速度的分布公式及电子发射系数公式，可得到该方程的解为空间环境温度T*，该解表明对于处于空间环境中的航天器，存在一个临界温度T*，使得航天器表面达到电流平衡状态。

如果考虑航天器具有初始电位φ，则粒子的能量受航天器表面电位影响，其速度分布将由f(E)变为f(E+eφ)，如此电流平衡方程也随之改变。对于麦克斯韦分布，其分布函数具有可分解特性，即存在一个与粒子能量无关的量：

(11)

使得：

(12)

由于式(11)、(12)中的因子g(eφ)只与表面电位有关，因此在表面带电的电流平衡方程中可以消去g(eφ)，消去后得到表面带电时的电流平衡方程与式(10)相同，该结果表明：在服从麦克斯韦分布的电子模型中，航天器表面电位对电流平衡无影响。

典型的介质表面二次电子发射(SecondaryElectronEmission,SEE)特性曲线如图2所示。该曲线上有两个δ(E)+η(E)=1的点，对应入射能量分别为E1(低能区临界点，即第一临界能量)和E2(高能区临界点，即第二临界能量)，该两点均满足电子的入射与出射数量相等，如图2所示，δ(E)+η(E)=1对应的两个临界点E1和E2将其划分为3个区域。当E11，即出射电子通量大于入射电子通量，表明相比于过低或过高的入射能量，中等能量的入射电子可以激发出较多的二次电子；当EiE2时，δ(E)+η(E)<1，即出射的电子通量小于入射电子通量，表明过低或者过高的入射能量都将降低介质表面的电子发射几率。

2 电子束撞击介质表面引发的带电

由于介质具有较高的绝缘性能，当电子束与介质表面相互作用时，介质表面产生的电荷不能以电流的形式流走，因此会在介质表面产生电荷的积累，积累的电荷会感应出对应强度的电场，从而影响后续入射电子束的能量及轨迹。

实际介质材料在微观原子量级时其表面较为粗糙，所积累的电荷及出射的电子受微观形貌影响较大；此外实际介质材料不可能完全绝缘，在电荷积累的过程中，会有很小一部分以微弱漏电流的方式流走。为简化电子与介质表面相互作用过程，考虑一种较为理想的介质，设其表面光滑且不会产生电荷泄漏，当电子束碰撞介质表面时，将有二次电子和背散射电子出射。设φf表示系统达到稳态后的最终电位，Ef表示系统达到稳态后入射电子的最终碰撞能量。下面分别考虑初始介质表面未带电、带负电和带正电(即φi=0，φi<0和φi>0)3种情况下，3种能量恒定的电子束流(即E1E2)分别持续轰击介质表面，当系统达到平衡时φf和Ef的计算分析过程。

2.1 电子束撞击未带电表面(φi=0)

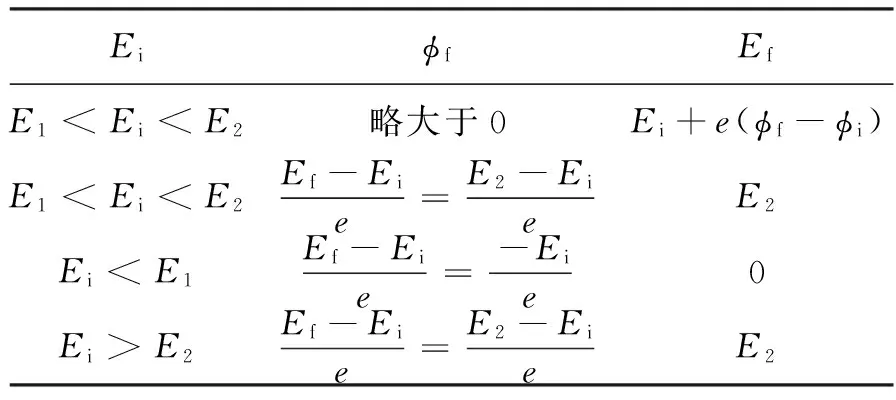
介质表面不带电时系统平衡状态分析如表1所示。

(1)碰撞能量大于第一临界能且小于第二临界能

情形1-1：当E1

(2)碰撞能量小于第一临界能

情形1-2：当Ei

(3)碰撞能量大于第二临界能

情形1-3：当Ei>E2时，出射电子通量亦小于入射电子通量，表面同样会产生电子的积累，积累的电子使得介质表面充电至负电位。充电至负电位的介质表面将会削弱入射电子的能量，使得束碰撞能量逐渐减小并逼近于E2。当介质表面的负电位持续增加到某一特定值使得束最终能量等于E2时，入射电子通量等于出射电子通量，此时该过程达到平衡，介质表面最终电位为使得束最终能量为E2的某一特定负值。

表1 介质表面不带电时系统平衡状态分析

2.2 电子束撞击初始带负电表面(φi<0)

介质表面带负电时系统平衡状态分析如表2所示。

(1)碰撞能量大于第一临界能且小于第二临界能

情形2-1：当E1

情形2-2：当E1

(2)碰撞能量小于第一临界能

情形2-3：当Ei

(3)碰撞能量大于第二临界能

情形2-4：当Ei>E2时，入射电子通量大于出射电子通量。当电子束持续轰击介质表面时，介质表面电子积聚，使得表面充电至更高的负电位，进而使得束碰撞能量减小。该过程将一直持续，直到最终电子束碰撞能量Ei减小到与E2相等，此时二次电子发射系数等于1，入射电子通量等于出射电子通量，表面的电位将不再改变。此种情形下，Ei=E2，最终电位是使得Ei=E2的某个特定值。

表2 介质表面带负电时系统平衡状态分析

2.3 电子束撞击初始带正电表面(φi<0)

介质表面带正电时系统平衡状态分析如表3所示。

(1)碰撞能大于第一临界能量且小于第二临界能

情形3-1：当E1

情形3-2：如果当E1

(2)碰撞能量小于第一临界能

情形3-3：当Ei

(3)碰撞能量大于第二临界能

情形3-4：当Ei>E2时，出射电子通量同样不能补偿入射电子通量，结果电子积累在表面，使得表面电位下降，束碰撞能量逐渐降低。直至束碰撞能量等于E2时，该过程达到平衡，此时最终的表面电位为使得束最终能量Ei=E2的某个特定值。

情形3-5：如果Ei>E2，且介质表面电位略微大于几个正伏特，出射电子通量大于入射电子通量，而大部分二次电子的能量很小，受正表面的束缚，不会发生逃逸，如果下降的束能量达到E2，而表面电位仍然略大于几个正伏特，则该过程会一直持续下去，直到表面电位低于几个正伏特，接近于零，即平衡状态，在该平衡状态时，二次电子能够逃逸。

表3 介质表面带正电时系统平衡状态分析

2.4 电子束撞击介质表面情况综述

从第2.1、2.2和2.3节的分析中可以看出，不同的表面带电情况及初始入射能量都将可能导致介质表面不同的充电行为。如图3所示，图中箭头形象地描述了12种初始情况下，单一能量电子束与介质表面持续作用后，系统的最终稳定状态。

图3所示的充电行为表明，临界能量E1、E2对于充电平衡状态均有明显的影响，但这两个临界点对于该系统而言却有不同的性质。对于E1，无论初始碰撞能量和初始表面电位如何变化，稳定时候的束碰撞能量都不会稳定在E1。综合分析介质表面的充电行为可以看出最终系统的稳定状态可分为3种：1)表面电势达到使得最终束碰撞能量为0的某一特定值，这种情况表示表面没有电子入射，故也不再存在电子出射和电荷积累；2)表面电势最终稳定在略大于0的状态(可近似为0)，这种情况下电子会从表面出射，但由于出射能量很小，会被表面微小的正电势吸引而无法逃逸，形成一种被“束缚”在介质表面的状态；3)表面电势达到使得最终束碰撞能为E2的某一特定负值，负的表面电势会对出射电子加速使其更容易发生逃逸，此时电子的入射量与出射量相同，系统达到平衡状态，不会再发生充放电行为。

3 介质表面带电对微放电发生的 影响

从第2节的分析中可以看出，当介质表面发生充放电行为时，不同的表面初始电位和碰撞能量都会影响系统最终的平衡状态。此外临界能量E1、E2对于系统平衡也表现出不同的影响，图3中显示高能端临界能量E2会较多地影响系统的最终束碰撞能量；而作为低能端判定电子出射产额的临界能量E1，在图3中未表现出对于系统平衡态有明显影响，但对于微放电效应来说，E1则是低能区判定电子是否满足倍增条件的关键量。

以介质填充微波部件为例对介质表面带电的微放电影响进行定性分析。图4给出了介质填充微波部件的典型结构示意。相比于双边金属极板结构，该结构除射频电场Erf以外，还存在由于介质表面电荷积累感应出的直流电场Edc。两个电场同时对位于两极板之间的带电粒子产生作用力。相比于单电场而言，在双电场的作用下粒子(包括初始电子和二次电子)的能量及运动轨迹不仅仅受到电磁波的作用，同时受到表面带电静电场作用，因此表面带电必然影响介质表面的微放电发生阈值。

3.1 单一能量电子束入射介质表面

材料表面的二次电子发射系数是除谐振条件以外，衡量微放电效应能否发生的关键指标。只有碰撞表面的入射电子束产生大于1的二次电子发射系数，才可能在谐振条件下产生倍增。在此认为入射介质表面的电子束能量单一，分别考虑低能和高能电子入射情况下，表面电位对于介质表面二次电子发射系数的影响规律。

(1)表面电位对E1的影响

当电子的入射能量较低时，低能区中使得二次电子发射系数为1的临界能量E1的大小决定了微放电发生阈值条件。如前文中公式(1)所述，电子与介质表面相互作用时，电子初始能量、碰撞能量、电荷量及初始表面电位存在特定的一次函数关系：Ei=Ep+eφi。若假设电子初始能量与第一临界能量相等(即：Ep=E1)，分别考虑初始介质表面带负电和带正电(即φi<0和φi>0)两种情况下碰撞能量Ei的大小：

1)若φi<0，Ei=Ep+eφi

2)若φi>0，Ei=Ep+eφi>Ep，Ei>E1，非平衡态，δ(E)+η(E)>1。

(2)表面电位对E2的影响

类似的分析也可以应用于表面电位对E2的影响规律。当电子以较高的能量入射介质表面时，决定微放电发生阈值条件的则是高能端临界能量E2。此时电子初始能量、碰撞能量、电荷量及初始表面电位存在关系：Ei=Ep+eφi。若假设电子初始能量与第二临界能量相等(Ep=E2)，分别考虑初始介质表面带负电和带正电(φi<0和φi>0)两种情况下碰撞能量Ei的大小：

1)若φi<0，Ei=Ep+eφi1；

2)若φi>0，Ei=Ep+eφi>Ep，Ei>E2，非平衡态，δ(E)+η(E)<1。

前述关于表面电势对于E1和E2的影响分析均为瞬态分析，即为电子束刚开始入射的一瞬间的表面状态。如果电子束持续轰击介质表面，则如第2节中所述，最终系统会达到一个使得出射电子数量与入射电子数量相同的平衡状态。其次，考虑到二次电子发射过程中，出射的电子能量大多集中在低能区域，高能区的二次电子数量很少，如若因为表面正电势的吸引而使得出射的二次电子再次撞击介质表面，其能量也不会有太大程度的改变，因此在上述分析中关于低能区临界能量E1的变化分析更具有代表性。

3.2 连续能量电子束入射介质表面

以上考虑均基于电子束能量单一情况，然而在实际的空间环境中，空间粒子束流的能量时刻变化，因此空间带电束流与介质表面作用的结果往往是以上多个状态的叠加，包括对介质表面电位、E1、E2和最终电子束碰撞能量的影响。值得注意的是，虽然表面电位会影响临界能量E1和E2的大小，但是使得二次电子发射系数大于1的能量范围不会改变。此处设二次电子发射系数大于1的能量区域宽度为ΔE，则ΔE与E1和E2之间存在如下关系：

(13)

当介质表面带负电时(φi<0)，E1和E2均被抬高了eφi，由于增加量相等，故ΔE的值不会发生变化。当介质表面带正电时也可以通过类似分析得到相同的结论。以上结论表明当表面带电时，ΔE不会发生变化，但是由于表面电位引发能量偏移，故会使ΔE区域内所对应的SEE曲线值发生改变，这种改变对于微放电的发生也存在一定的影响。

若入射电子束的能量为连续能量，则表面带电对于微放电发生的影响与单能电子束入射介质表面时存在明显差异。此处假设入射电子束的能量连续且其数量在能量上下限之间服从均匀分布，并设Em和En分别为能量区域的上下限。根据电子出射的物理意义和数学上积分的几何意义可知，对图1中曲线在某特定能量区域内进行积分，可以得到该能量区域内的总电子发射系数，总电子发射系数除以该能量带宽度即可得到该能量区域内的平均电子发射系数，根据之前的分析可知，能量带宽度不随表面电位的变化而变化，因此平均电子发射系数与积分得到的总电子发射系数呈现正比例关系。在此对Em和En区域内的SEE曲线进行积分，可以得到能量均匀分布于该区间时的总二次电子发射系数，此处设区间(Em,En)的积分结果(即总电子发射系数)为N，平均电子发射系数为n，则N与n存在如下关系：

(14)

(1)负表面电位的影响

(15)

为便于分析，定义图5中峰值所对应的能量值为Emax，且考虑到如果n*<1，则不存在发生微放电的风险，故以下讨论中均不考虑使得n*<1的情况：

1)若En

3)若EmNn、NmNn，则电子发射系数增加，微放电发生风险增加；反之则微放电发生风险降低。

(2)正表面电位的影响

(16)

此时也存在3种情况，(以下讨论中也不考虑使得n*<1的情况)：

2)若Em>Emax，则Nm>Nn，根据公式(16)可知N*

3)若EmNn、Nm

以上关于介质表面带电时，连续能量电子束轰击介质表面的分析结果表明：介质表面带电会很大程度上改变入射电子束的能量范围，从而影响微放电的发生。在此过程中，平均电子发射系数n*为衡量是否具备微放电发生条件和微放电发生风险提高或降低的重要指标。

4 结束语

本文综合分析了恒定能量的电子束流持续轰击不同初始电位介质表面时，介质表面电位及电子束流碰撞能量的变化趋势；通过分析及计算，得出了系统平衡后的电子束流碰撞能量和介质表面电位的理论计算结果；并以介质填充微波部件为例剖析了单一能量及连续能量电子束入射介质时，表面带电对于临界能量和微放电发生的影响。理论分析过程表明：

1)表面电位对于电子束轰击介质表面时的电流平衡状态没有影响；过高或过低的电子碰撞能量都会导致较小的二次电子产额；较大的二次电子产额一般发生在中间能量区域(E1

2)不同的介质表面初始电位和电子束碰撞能量都会较为明显地影响系统的最终平衡状态，且系统平衡状态受E2影响显著。

3)介质表面带电会使电子束的入射能量发生偏移，引起介质表面的电子发射系数的改变，进而影响微放电发生的风险。

本文综述分析了介质表面的带电现象及其对微放电发生风险的影响，而介质表面二次电子发射及其在电磁场中运动和倍增瞬态过程的准确分析还有待于今后继续开展相关研究工作。

References)

[1] KISHEK R A, LAU Y Y, ANG L K, et al. Multipactor discharge on metals and dielectrics: historical review and recent theories[J]. Physics of Plasmas, 1998, 5(5):2120-2126.

[2] SEMENOV V E, RASCH J, RAKOVA E, et al. General study of multipactor between curved metal surfaces [J]. IEEE Transactions on Plasma Science, 2014, 42(42):721-728.

[3] ARREGUI I, TEBERIO F, ARNEDO I, et al. High-power low-pass harmonic filters with higher-order, and non-mode suppression: design method and multipactor characterization[J]. IEEE Transactions on Microwave Theory & Techniques, 2013, 61(61):4376-4386.

[4] ANZA S, VICENTE C, GIL J, et al. Prediction of multipactor breakdown for multicarrier applications: the quasi-stationary method[J]. IEEE Transactions on Microwave Theory & Techniques, 2012, 60(7):2093-2105.

[5] KISHEK R A, LAU Y Y. Multipactor discharge on a dielectric[J]. Physical Review Letters, 1998, 80(1):3198-3200.

[6] VAUGHAN J R M. Multipactor[J]. Electron Devices IEEE Transactions on, 1988, 35(7):1172-1180.

[7] 崔万照, 杨晶, 张娜. 空间金属材料的二次电子发射系数测量研究[J]. 空间电子技术, 2013, 10(2):75-78.

CUI W Z, YANG J, ZHANG N. Testing method of the secondary electron emission yield of space metal materials[J]. Space Electronic Technology, 2013,10(2):75-78(in Chinese).

[8] RASCH J, JOHANSSON J F. Non-resonant multipactor—a statistical model[J]. Physics of Plasmas, 2012, 19(12):1-33.

[9] 曹桂明, 聂莹, 王积勤. 微波部件微放电效应综述[J]. 宇航计测技术, 2005, 25(4):36-40.

CAO G M, NIE Y, WANG J Q. Multipactor on microwave components[J]. Journal of Astronautic Metrology & Measurement, 2005,25(4):36-40(in Chinese).

[10] 张娜, 崔万照, 胡天存, 等. 微放电效应研究进展[J]. 空间电子技术, 2011(1):38-43.

ZHANG N, CUI W Z, HU T C. Advances in Research on Multipactor[J]. Space Electronic Technology, 2011(1):38-43(in Chinese).

[11] 王德甫. 微波部件微放电特性与抑制的研究[D]. 哈尔滨：哈尔滨工业大学, 2010:3-4.

WANG D F. Research on the characteristic and suppression of multipactor in microwave device[D]. Harbin: Harbin Institute of Technology, 2010:3-4(in Chinese).

[12] 陈建荣, 吴须大. 星载设备中的微放电现象分析[J]. 空间电子技术, 1999(1):19-23.

[13] SAZONTOV A, BUYANOVA M, SEMENOV V, et al. Effect of emission velocity spread of secondary electrons in two-sided multipactor[J]. Physics of Plasmas, 2005, 12(5):1133-101.

[14] SEVIOUR R. The role of elastic and inelastic electron reflection in multipactor discharges[J]. Electron Devices IEEE Transactions on, 2005, 52(8):1927-1930.

[15] SEMENOV V E, RAKOVA E I, ANDERSON D, et al. Importance of reflection of low-energy electrons on multipactor susceptibility diagrams for narrow gaps[J]. Plasma Science IEEE Transactions on, 2009, 37(9):1774-1781.

[16] SEMENOV V, NECHAVE V, RAKOVA E, et al. Multiphase regimes of single-surface multipactor[J]. Physics of Plasmas, 2005, 12(7):073508-073508-6.

[17] CHANG C, VERBONCOEUR J, TANTAWI S, et al. The effects of magnetic field on single-surface resonant multipactor[J]. Journal of Applied Physics, 2011,110(110):063304-063304-5.

[18] CHANG C, LIU G Z, TANG C X, et al. Suppression of high-power microwave dielectric multipactor by resonant magnetic field[J]. Applied Physics Letters, 2010, 96(11):111502-111502-3.

[19] 韩晨, 周东方, 余道杰,等. 混合场介质表面单边次级电子倍增效应统计[J]. 强激光与粒子束, 2014, 26(8):179-184.

CHEN H, ZHOU D F, YU D J, et al. Statistical prediction of dielectric single-surface multipactor discharge under mixed field[J]. High Power Laser & Particle Beams, 2014,26(8):179-184(in Chinese).

[20] DIAZ N, CASRANEDA S, RIPALDA J M, et al. Materials of low secondary electron emission to prevent the multipactor effect in high-power RF devices in space[C]. 6th Spacecraft Charging Technology. AFRL Science Center ,Hanscom AFB,MA,USA,November 2-6,1998.

[21] POPOVIC S, VUSKOVIC L, SAMOLOV A, et al. Secondary electron emission and multipactor discharges[C].The Second International Conference on Radiation and Dosimetry in Various Fields of Research,RAD 2014,Nis,Serbia,May 27-30,2014.

(编辑：车晓玲)

Surface charging analysis induced by electron beam impact dielectric

WANG Dan1，HE Yongning1,*，LI Yun1,2

1.SchoolofElectronicandInformationEngineering,Xi′anJiaotongUniversity,Xi′an710049,China2.NationalKeyLaboratoryofScienceandTechnologyonSpaceMicrowave，ChinaAcademyofSpaceTechnology(Xi′an)，Xi′an710100，China

For existing multipactor occurred in dielectric microwave components, more attention is paid to multipactor source and suppression from the aspect of resonance and emitted electron yield, while the study about influence of surface potential on multipactor is rarely reported. Secondary electron emission characteristics were analyzed. Final surface potential and electron impact energy were emphatically studied when electron beam with constant energy sostenuto impacted the dielectric surface with various initial surface potential. Surface potential and electron impact energy were calculated when the system became stable.Calculated data indicates that steady state of the system is remarkably influenced by primary energy and the second critical energy. The influence of surface potential on secondary electron emission was systematically studied when electrons with single and continuous energy impacted the dielectric surface. An -eφenergyshiftingofcriticalenergyisrevealedwhensurfacepotentialisφ.Forelectronbeamwithcontinuousincidentenergy,impactenergyrangeisdramaticllyeffectedbysurfacepotentialofthedielectric,andtheriskofmultipactorisfurtherinfluenced.

spacecraft surface charging；secondary electron emission；impact energy；surface potential；multipactor

10.16708/j.cnki.1000-758X.2017.0031

2016-08-31；

2017-03-02；录用日期：2017-03-17；

时间：2017-03-21 15:59:38

http://kns.cnki.net/kcms/detail/11.1859.V.20170321.1559.012.html

国家自然科学基金(U1537211)

王丹(1992—)，男，博士研究生，469599697@qq.com，研究方向为材料表面处理及二次电子发射

*通讯作者：贺永宁(1971—)，女，教授，yongning@mail.xjtu.edu.cn，研究方向为ZnO宽禁带半导体、微波无源器件和电路

王丹,贺永宁,李韵.电子束撞击介质表面引发的带电现象分析[J].中国空间科学技术,2017，37(2):1-10.

WANGD,HEYN,LIY.Surfacecharginganalysisinducedbyelectronbeamimpactdielectric[J].ChineseSpaceScienceandTechnology, 2017,37(2): 1-10 (inChinese).

TN

A

http://zgkj.cast.cn