山西省城镇居民消费和支出分析预测

王艳丽，朱家明

（安徽财经大学 经济学院，安徽 蚌埠 233030）

山西省城镇居民消费和支出分析预测

王艳丽，朱家明

（安徽财经大学 经济学院，安徽 蚌埠 233030）

本文以山西省为例，分别搜集山西省1995-2014年间人均消费支出和人均可支配收入的数据.首先用散点图判断收支间具有的的相关关系，再通过EViews软件建立模型并进行分析检验，进而对山西省城镇居民消费和支出情况作出预测.

EViews；回归；JB检验

0 引言

自改革开放以来，山西省经济增长不断加快，居民消费和支出也在不断提高.城镇居民的消费和支出是体现经济状况的重要指标之一，有助于衡量当地经济持续发展能力并体现居民生活水平优劣.

浙江师范大学的郑红宾、陈雄（2011）运用E-views软件对浙江金华城镇居民的消费与支出进行分析预测，但所选取的地区具有偶然性，不够全面.咸宁学院的陈敏、周志朋（2008）同样利用EViews建立回归方程并分析预测，但其对于预测结果的分析不够清晰.

综上，现有研究缺乏针对区域性居民消费和支出的全面分析.

本文以山西省为例，分别搜集山西省1995—2014年间人均消费支出(Y)和人均可支配收入(X)的数据.首先用散点图判断收支间具有的的相关关系，再通过EViews软件建立模型并进行分析检验，进而对山西省城镇居民消费和支出情况作出预测.

1 数据的收集

笔者所收集的数据如表1所示，就表1看来，自1995到2014年间，山西省城镇居民人均消费支出和人均可支配收入都在不断提升，其中人均消费支出上涨了4.54倍，人均可支配收入上涨了6.29倍.在这20年间，收入上涨的倍数大于消费且两者间的比值不断增加，由1995年的1.25上升到2014年的1.64.

综上可知，这20年来山西省城镇居民的经济状况得到不断改善.

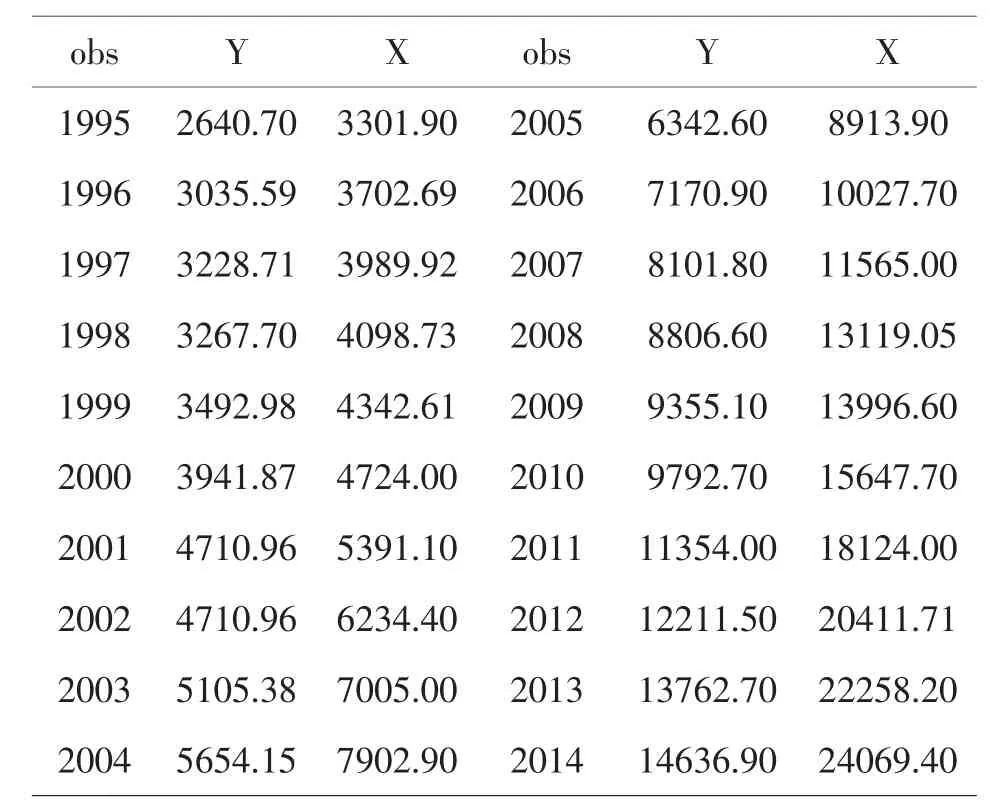
表1 1995—2014年山西省城镇居民人均消费支出与人均可支配收入

2 模型的建立

2.1 绘制散点图

根据表1中的数据，在EViews软件中绘制Y与X间的散点图，得到如图1所示结果.

由图1可知，在1995—2014这20年间，Y与X间呈一元线性关系，可建立模型形式：

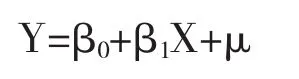
式中：μ——随机扰动项

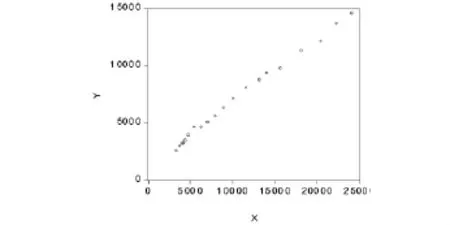
图1 Y与X散点图

在EViews软件中，一元线性方程的建立主要通过最小二乘法实现，但最小二乘法的运用具有四个假设前提.其中最小二乘法对模型中随机扰动项μ的要求是μ符合正态分布.在判断μ是否符合正态分布时，我们无法直接观测到μ，因此需要通过对残差μ进行分析来检验μ.

2.2 JB检验

JB检验是通过JB统计量进行正态性检验的方法.JB统计量全称为Jarque-Bera统计量，是根据残差ei对大样本是否符合正态分布进行检验的数学方法.

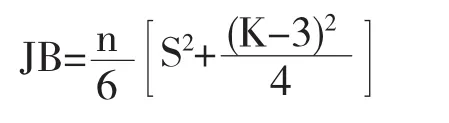
式中：n——样本容量

当大样本为正态分布时，JB检验量服从如下卡方分布：

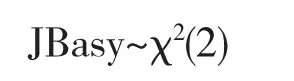
式中：asy——渐进的

综上可知，如果被测样本符合正态分布，则S=0，K=3，JB=0；若被测样本不符合正态分布，则JB的值将不断增大.给定显著性水平α=0.05，查表可知χ2(2)=5.99147.通过对表1中数据的一般统计特征（表2）的计算，得到JB检验量的值，进而判断是否符合正态分布，能否用最小二乘法进行计算，如果计算值超过5.99147，拒绝原假设即不符合正态分布假设，反之样本则为正态分布.

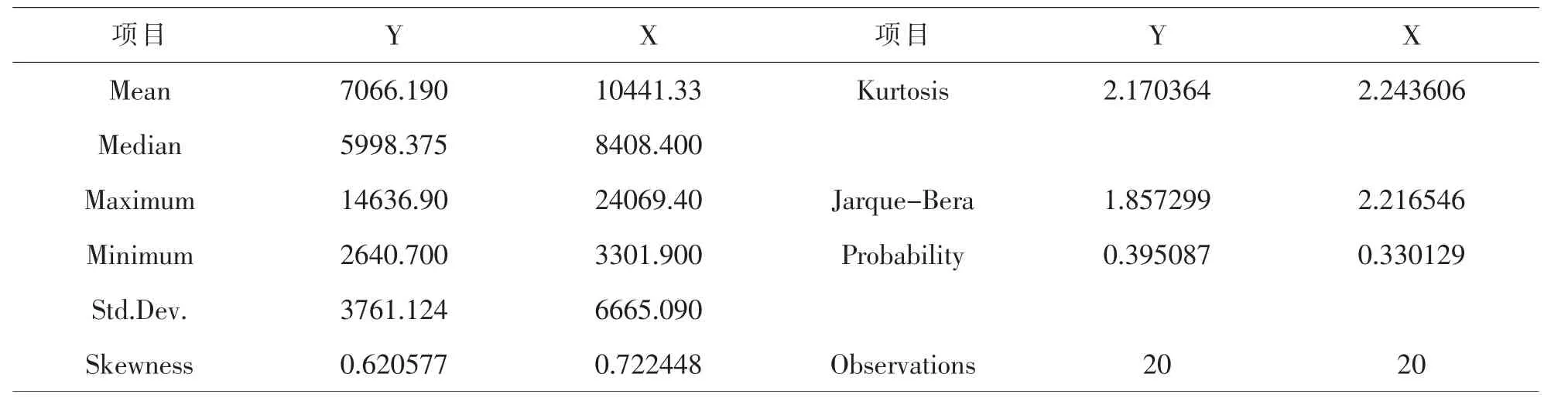
表2 数据的一般统计特征

由表2计算可知，S=0.0001，K=0.6502，JB=4.6013< 5.99147，所以该数据符合正态分布，可以用最小二乘法进行计算.

2.3 一元线性回归

经过上述分析，可以用建立一元回归方程的形式表示Y与X间的关系，用EViews回归所得结果如表3：

表3 一元回归结果

该一元回归方程拟合程度较高，各回归参数显著，方程总体显著性较好，说明该方程可以用来表示山西省城镇居民人均消费支出与人均可支配收入间的关系.

3 模型的预测

首先通过EViews做出被解释变量拟合值与真实值偏差的模型预测图，拟合值记做YF，如图2所示；再做出该模型的拟合和残差图，如图3所示.可以看出偏差百分比接近0，说明该模型预测精度较高.

利用表1中的数据可知2010—2014年间人均可支配收入（X）的平均年增长率为11.37%，仍以此增长可计算出2015—2019年间的人均可支配收入为26806.09,29853.94,33248.34,37028.67,41238.83，运用EViews推测出人均消费支出如表3所示.通过表3可知之后5年预测消费支出分别为16277.42，17993.06，19903.76，22031.71，24401.61.

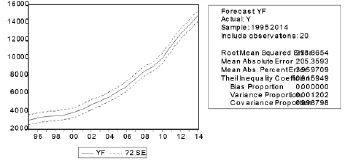
图2 模型预测图

图3 模型的拟合图与残差图

表3 2015—2019消费支出预测

4 结论与建议

随着经济社会的不断发展，城镇居民的经济状况不断改善，其购买力也在不断提升，通过收入预测未来消费支出水平对于把握经济动态发展，调整宏观调控政策具有重大意义.笔者通过EViews软件绘制山西省人均消费支出与人均可支配收入间的散点图，显示二者间存在一元线性相关关系.进而建立相关模型，并对模型进行检验，可通过一个已知量求出另一个未知量，也可用该模型预测未来数据.

由方程Y=1188.274+0.5629X可以看出，X与Y之间呈一元正相关关系，即Y随着X的增加而增加，收入X每变动1个单位，消费Y相应的变动0.5629个单位，即收入中的56.29%将用于支出.其中1188.274可以看做1995—2014年间人均每年的自发性消费.

收入中超过半数将用于消费，约为56.29%，在拉动GDP的同时也体现出城镇居民对生活的追求.但若能通过一定方式刺激消费，将收入中的更多用于支出，将有利于经济的迅速恢复.比如调整税收政策，加大转移支付；开发创新领域，吸引消费者；适当降低信贷要求，给低收入者更多机会等.

〔1〕陈启蕊.基于EViews软件的云南省城镇居民消费和支出分析预测[J].玉溪师范学院学报,2013 (12):36-40.

〔2〕郑红宾,陈雄.基于EViews软件对金华城镇居民的消费和支出进行分析预测[J].枣庄学院学报, 2011(05):84-88.

〔3〕刘猛,王桂荣,王慧军.河北省农村居民生活消费支出倾向分析[J].安徽农业科学,2010(03):1478-1481.

〔4〕陈敏,周志明.基于EViews软件对某地区的消费和支出进行分析预测 [J].咸宁学院学报,2008 (06):8-11.

〔5〕李路.我国政府消费支出与经济增长关系的实证分析[D].西南财经大学,2009.

〔6〕余晓春.1978—2005年中国居民消费支出结构研究[D].湖南师范大学,2007.

〔7〕马立平.居民消费的定量研究[D].首都经济贸易大学,2006.

F126.1

A

1673-260X（2017）04-0072-03

2017-01-11

国家自然科学基金资助项目（11301001）

朱家明（1973-），男，安徽泗县人，副教授，硕士，安徽财经大学数学建模实验室主任，研究方向：应用数学与数学建模