地铁杂散电流动态分布模型研究*

张栋梁 刘 娟 谢业华 黄 开 刘 振

(中国矿业大学电气与动力工程学院,221116,徐州//第一作者,副教授)

地铁杂散电流动态分布模型研究*

张栋梁 刘 娟 谢业华 黄 开 刘 振

(中国矿业大学电气与动力工程学院,221116,徐州//第一作者,副教授)

分析单边供电与双边供电下的杂散电流静态分布模型。根据列车的速度、位置、取流大小等随时间发生变化的情况,以轨道-排流网-埋地金属-大地结构的杂散电流静态模型和牵引计算为基础,设计双边供电方式下基于时间-位置-取流变化的杂散电流动态分布模型,并对模型进行计算求解,实现三维仿真。分析杂散电流和轨电位在不同工况下的动态分布规律,得出特定位置杂散电流和轨电位随时间的动态分布。

地铁; 直流牵引; 杂散电流; 动态分布模型

Author′s address School of Electrical and Power Engineering, China University of Mining and Technology,221116,Xuzhou,China

目前,我国城市轨道交通系统采用750 V和1 500 V两种电压等级,列车利用车厢上方受电弓与牵引网接触获得电能,从列车流出的电流通过走行轨回流至牵引变电所与负母排相连。由于钢轨内阻的存在以及轨地之间不能做到完全绝缘,轨地之间存在压降,列车运行过程中总会有部分电流经走行轨流入大地,再经大地流回钢轨至牵引变电所,或经过大地直接回流至牵引变电所。这部分泄漏到大地的电流称为杂散电流,也称为迷流[1-2]。

1 地铁供电系统运行方式

牵引变电所对接触网的供电方式有单边、双边和越区供电三种[3]。单边供电是指供电臂只从一端的变电所取得电流的供电方式,即一座牵引变电所独立为列车供电。双边供电是指供电臂从相邻的两个变电所取得电流,即两端相邻的变电所同时给列车供电。越区供电是指当某一牵引变电所因故障不能正常供电时,相邻牵引变电所通过本身的供电臂,再经分区所的开关设备给故障牵引变电所供电臂临时供电的方式。

单边供电和双边供电为正常的供电方式,而越区供电是一种非正常供电方式(也称事故供电方式)。在城市轨道交通系统中,在相同供电距离的情况下,双边供电较单边供电具有明显优势,单边供电的电压损失、杂散电流危害程度均是双边供电的3～4倍。因此,列车在正线行驶期间,一般都釆用双边供电方式。单边供电方式只在车场、试车线路等特殊地段采用。

2 杂散电流动态分布模型

2.1 静态模型

杂散电流动态分布模型的建立是以静态模型为基础的,因此需首先分析两种正常供电方式下杂散电流的静态分布模型[4-6]。

为建立杂散电流静态模型,作如下假设:

(1) 轨道的纵向电阻分布是均匀的;

(2) 轨道对排流网的过渡电阻和土壤电阻分布是均匀的;

(3) 排流网电阻分布是均匀的;

(4) 排流网对埋地金属的过渡电阻分布是均匀的;

(5) 埋地金属结构电阻分布是均匀的;

(6) 接触网自身阻抗忽略不计;

(7) 不考虑大地纵向电阻的影响。

目前,单边供电方式下杂散电流静态分布模型的建立主要基于轨道-大地电阻、轨道-埋地金属-大地电阻、轨道-排流网-埋地金属-大地电阻(见图1)等3种结构。图1中,Rg为轨道的纵向电阻;Rj为轨道对大地的过渡电阻;Rp为排流网的纵向电阻;Rj1为排流网对埋地金属的过渡电阻;Rs为埋地金属的纵向电阻;Rj2为埋地金属对地的过渡电阻;i为轨道x处的电流;ip(x)为列车位置x处排流网的电流;is(x)为埋地金属结构在列车位置x处的泄漏电流;I是两牵引所为列车提供电流的总和;x是列车位置距离牵引变电所的里程。

图1 轨道-排流网-埋地金属-大地的电阻网络

双边供电方式看作是两个单边供电方式的叠加。因此,静态模型的分析均可参考单边供电方式。本文在轨道-排流网-埋地金属-大地电阻结构的基础上建立双边供电的模型,同时假设两牵引变电所之间的母线电压相等,得出两个牵引变电所之间的杂散电流分布规律。

双边供电方式下,I1代表列车从牵引变电所1取电流;I2代表列车从牵引变电所2取电流,且I=I1+I2;L1为列车到牵引变电所1的距离,L2为列车到牵引变电所2的距离,且L1+L2=L。以列车为分界点将两牵引变电所划为0～L1区段和L1～L2区段。由此可得如下关系:I1=I·L2/L,I2=I·L1/L。

2.2 双边供电动态模型

本文建立的双边供电杂散电流动态模型是基于时间-位置-取流变化的。由图2所示列车取流情况可以看出,列车距离牵引变电所的位置不同,供电臂取流不同。此外,不同工况下,列车从牵引变电所取流大小、列车位置、列车加速度、列车速度等是随时间不断变化的。依据这些变化对已建立的杂散电流模型的条件进行修改,可使静态模型转化为动态模型。

图2 列车取流情况

双边供电杂散电流动态分析流程图如图3所示。先导入基本数据,其中牵引计算结果I(t)、s(t)设为已知量,以时间t为步长,每次读取当前时刻的取流电流值I和位置s,根据建立的轨道-排流网-埋地金属-大地电阻结构下的杂散电流分布模型,对列车运行两侧区间分别独立设置边界条件和运算求解微分方程,并保存修改结果,进入到下一次循环,直到达到区间的总运行时间T结束。

建立轨道-排流网-埋地金属-大地结构的杂散电流静态分布模型,在此基础上,通过编程建立基于时间-位置-取流变化的动态分布模型。

3 基于时间-位置-取流的动态模型仿真分析

在进行杂散电流动态分布模型仿真分析时,各参数的取值范围如下:

(1) 列车取流范围:500～3 000 A;

(2) 列车行驶区间距离:1～3 km;

(3) 各层之间过渡电阻取值范围:1～15 Ω·km;

(4) 钢轨纵向电阻:0.000 1～0.1 Ω/km;

(5) 排流网的纵向电阻:0.000 1～1 Ω/km;

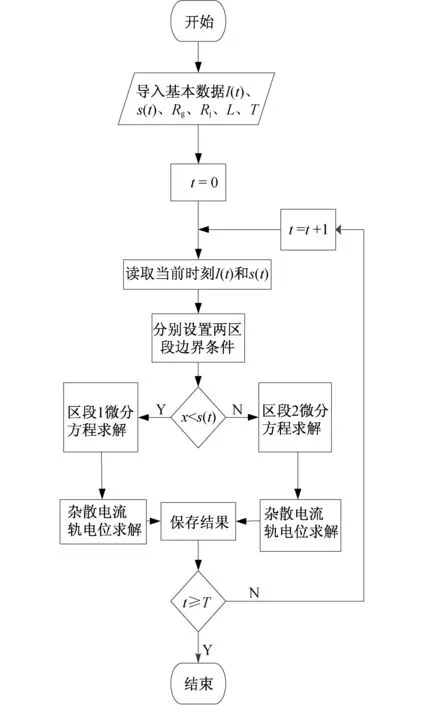
图3 双边供电杂散电流动态模型计算流程图

(6) 埋地金属结构纵向电阻:0.01～1 Ω/m。

列车的实际运行工况是在两个牵引变电所之间进行加速、匀速(惰行)以及制动减速。本文在传统的杂散电流静态模型的基础上,引入列车牵引计算的概念,根据模拟的列车运行工况(最快运行策略)和已建立的基于时间-位置-取流的动态模型,进行复杂运行工况下连续的杂散电流规律的分析。

设Rg=0.026 Ω/km,Rp=0.001 Ω/km,Rs=0.01 Ω/km,Rj=15 Ω·km,Rj1=Rj2=3 Ω·km,L=3 km,牵引电压UD=1 500 V。I根据列车不同运行工况而变化。

图4、5、6分别为根据动态模型仿真得出的轨电位、走行轨回流电流、杂散电流分布三维图,可以看出,三维图可具体形象地展示列车在区间内运行时,某时刻不同位置或某位置不同时刻相关电气量的变化情况。

由图4可知,列车运行的前140 s为加速和匀速运行过程,列车由加速阶段进入匀速惰行阶段的过程中轨电位逐渐升高并达到峰值,但此时列车取流并不是最大值。因为峰值时刻列车所处位置在1.35 km左右,距离两侧牵引所相对较远。图4中类似磁滞回线的色带周边部分相当于列车向两牵引所分别回流过程中轨电位过零点附近的变化情况。此处轨电位最低。另外,在列车起动初期及列车制动进站末期,轨电位幅值也较小。在140～160 s列车减速制动阶段,制动初期轨电位较高,这是因为列车制动将能量反馈回电网,有较大的冲击电流而引起轨电位过高。列车在实际运行过程中,应避免频繁的制动和加速,这有助于减小轨电位。

图4 轨地电位分布图

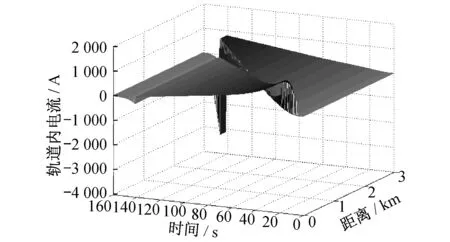
图5 走行轨回流分布图

由图5可知,轨道内电流与列车取流规律相符,说明大部分电流通过钢轨回流。钢轨内电流流量可间接反应列车取流的情况,在列车起动初期需提供较大的加速度以进入匀速运行阶段,此时轨道内电流较大,随着时间的推移,轨道内近起点处电流逐渐减小,近终点处电流逐渐增大。在进入制动阶段后,轨道内逆向电流相对制动前电流大得多(仿真中未考虑能量回馈吸收)。

图6 杂散电流分布图

图6中,两个波峰之间的部分是列车行驶位置杂散电流的呈现,其杂散电流较小,接近零值。这是因为列车处于起动初期、制动停车末期时取流较小,且存在部分杂散电流经钢轨回流的情况。图6中深色区域杂散电流的泄漏最为严重。列车运行140 s后进入制动阶段,图6中①区域表示列车制动状态的杂散电流情况,在制动阶段有较大的电流向电网回流,能量回馈吸收装置能减小列车在制动时的回流电流,有助于抑制电化学腐蚀。

区别于静态模型只能反映某一时刻杂散电流和轨电位的分布情况,动态模型可用于分析特定位置杂散电流和轨电位随时间的变化。图7和图8分别为列车在区间100 m、750 m、1 500 m、2 250 m、2 900 m等特定位置处轨电位和杂散电流随时间的变化情况。在加速和匀速运行阶段,轨电位随着列车距两变电所距离的增加而变大,呈单峰曲线变化规律,轨电位在列车位置处达到最大;杂散电流呈双峰形规律变化,在列车位置处最小。在制动阶段,由于列车制动后电流反向,轨电位较前一阶段方向取负,变化规律一致;杂散电流在此阶段方向取负,并逐渐减小。

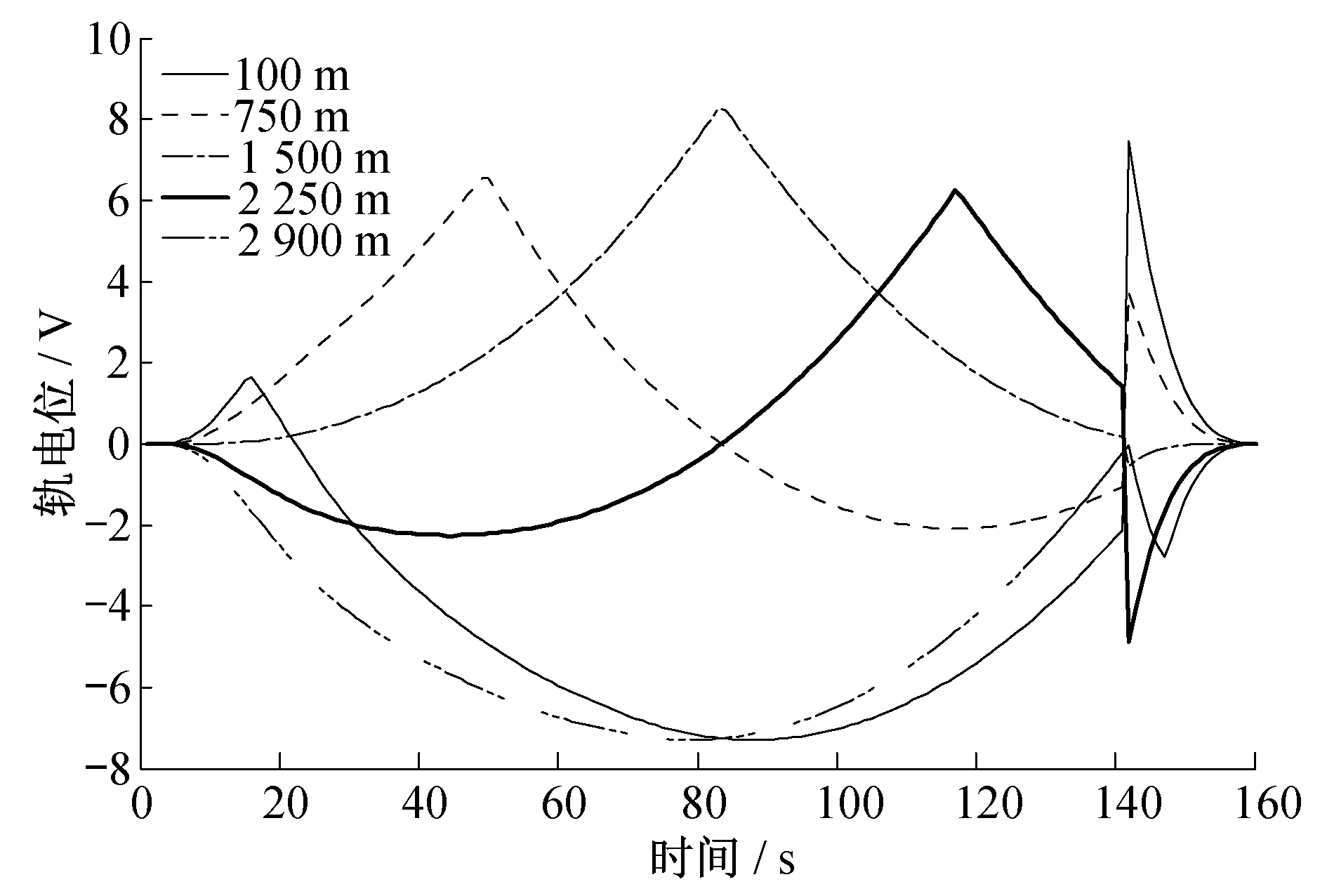
图7 特定位置轨电位分布图

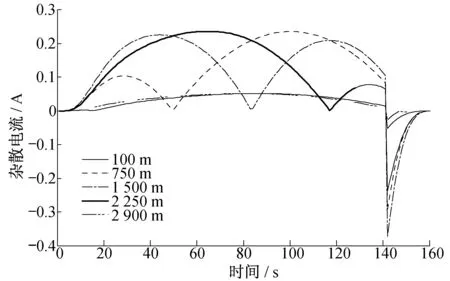
图8 特定位置杂散电流分布

此外,列车在区间内运行的动态仿真,对杂散电流监测环节中的传感器设置具有指导作用,可以根据杂散电流的分布规律以及现场实际情况确定传感器埋设位置。

4 结语

本文构建了单边供电和双边供电方式下轨道-排流网-埋地金属-大地结构静态模型。以静态模型和牵引计算为基础,设计了基于时间-位置-取流变化的动态模型。借助动态模型完成了杂散电流三维分布规律的仿真,得到列车在任一位置时,杂散电流随时间的动态分布。分析杂散电流的动态分布规律,可为下一步的安全防护作出指示。

[1] 申宁,李群湛,刘炜.不均匀过渡电阻下地铁杂散电流分析[J].都市快轨交通,2010(6):37-45.

[2] 李威.地铁杂散电流腐蚀监测及防护技术[M].徐州:中国矿业大学出版社,2004:8-16.

[3] 张福生.牵引供电系统[M].北京:北京交通大学出版社,2013:20-22.

[4] 苏晓舟,顾保南,孙世超.2013年中国城市轨道交通运营线路统计和分析[J].城市轨道交通研究,2014(1):1-6.

[5] 刘燕,王京梅,赵丽.地铁杂散电流分布的数学模型[J].工程数学学报,2009,26(4):571-576.

[6] 朱晓敏,徐振华.基于单质点模型的城市轨道交通列车动力学仿真[J].铁道学报,2011(6):55-60.

[7] 秦峰,朱祥连,奚杰,等.城市轨道交通设施杂散电流的防护[J].机电工程,2013(1):102-107.

Evaluation and Analysis of Dynamic Stray Current in DC Metro System

ZHANG Dongliang, LIU Juan, XIE Yehua, HUANG Kai,LIU Zhen

The static distribution model of stray current under the circumstance of single side feeding and single locomotive is analyzed.According to the changes in locomotive′s speed,position and streams over time,by using the static model of “track-drainage net-buried metal-earth structure” and traction calculation,the dynamic stray current distribution model is designed and calculated based on “time-positionflow” changes,in order to realize a 3D dynamic simulation.By analyzing the dynamic distribution of stray current and rail potential under different conditions,the dynamic stray current and rail potential distribution on specific spot with time is obtained.

metro; DC transit system; stray current; dynamic distribution model

*国家自然科学基金项目(51147011)

U223.6+2

10.16037/j.1007-869x.2017.04.014

2015-05-29)