电控单体泵高速电磁阀多目标优化分析

张建宇， 范立云， 袁航

(1.中国船舶重工集团公司第七一三研究所 第六研究室，河南 郑州 450052； 2.哈尔滨工程大学 动力与能源工程学院，黑龙江 哈尔滨 150001)



电控单体泵高速电磁阀多目标优化分析

张建宇1， 范立云2， 袁航1

(1.中国船舶重工集团公司第七一三研究所 第六研究室，河南 郑州 450052； 2.哈尔滨工程大学 动力与能源工程学院，黑龙江 哈尔滨 150001)

针对高速电磁阀的延迟响应会引起喷油定时失准以及循环喷油量的精度变差，进而导致柴油机排放超标及油耗增加等问题，本文开展了电磁阀结构多目标优化与分析，最终可以达到电磁阀延迟响应最小化的目的。本文应用AMESim软件建立电控单体泵仿真模型，经过实验验证了模型准确性。通过实验设计的方法对影响电磁阀响应延迟的关键参数进行预测。得出关键影响参数：衔铁残余气隙、弹簧预紧力、锥阀半锥角、阀杆直径及锥阀直径。应用多目标多学科优化平台modeFRONTIER，采用NSGA-Ⅱ遗传算法，以电控单体泵高速电磁阀开启、关闭响应延迟时间作为目标建立多目标优化模型。优化结果显示：关闭延迟时间减小了6%，开启延迟时间减小了17.7%，喷油压力峰值增大0.62 MPa，有利于进一步提高循环喷油量控制的精确程度。

电控单体泵；高速电磁阀；多目标优化；AMESim；响应延迟；modeFRONTIER；柴油机；排放；喷油量

电控单体泵是一种能够满足当前柴油机排放法规和经济性要求的新型燃油喷射系统，可实现较高的喷油压力及良好的燃料雾化[1]。高速电磁阀(简称电磁阀)是电控单体泵的核心组件之一，它的响应速度决定了喷油压力的建立与喷射后油压卸载速度等特性，从而会影响到喷油系统的喷油定时、循环喷油量等关键特性[2]。电磁阀较大的响应延迟会引起喷油定时失准和循环喷油量的精度变差，从而导致柴油机排放超标及油耗增大。为进一步提高喷油控制的精确性，需要对影响电磁阀响应的关键特性参数进行优化设计，以减小电磁阀的响应延迟时间。

目前，国内在电磁阀的铁芯材质、驱动电路设计等方面进行了较多的实验研究和优化设计。张奇等对电控柴油机的电磁阀驱动电路进行了分析，通过有限元软件Ansys对电磁阀进行有限元建模，模拟了电磁阀关闭动态响应过程，并对驱动电路进行优化设计，降低了电磁阀闭合响应时间[3]。张廷羽等通过Ansys分析电磁阀的电磁部分，利用AMESim建立了电磁阀整体仿真模型，对影响电磁阀的各个因素进行了计算和分析，并提出了适合电磁阀铁心材质、线圈等优化设计的方案[4]。李铁栓等采用模拟退火算法，结合电磁阀Ansys有限元仿真模型，通过多目标优化平台modeFrontier对高压共轨电磁阀的开启、关闭延迟时间进行优化设计，降低了电磁阀的开启和关闭延迟时间[5]。

以上所述对电磁阀的优化设计皆把电磁阀作为独立系统进行优化设计，本文把电磁阀作为电控单体泵系统中的一部分进行电磁阀延迟响应时间优化，并分析优化后对电控单体泵系统喷射特性的影响。本文在AMESim环境下建立电控单体泵仿真模型，并结合试验数据对模型的准确性进行验证。应用实验设计方法，对电控单体泵电磁阀部分各特性参与电磁阀响应延迟时间的相关性进行深入分析，得到电磁阀响应的关键影响参数。进而利用多目标优化平台modeFRONTIER与AMESim进行联合仿真，对电磁阀响应时间的关键影响参数进行优化，以获得电磁阀与电信号的开启和关闭延迟最小响应时间。

1 电磁阀结构组成及工作原理

1.1 电磁阀工作原理

电控单体泵及电磁阀的结构如图1所示，主要包括电磁阀控制部分和柱塞加压部分：柱塞加压部分包括柱塞、柱塞套和柱塞弹簧；电磁阀控制部分主要包括电磁铁、衔铁、控制阀杆、衔铁复位弹簧、出油堵头等零部件。通电后，电磁铁吸合衔铁，拉动控制阀杆，关闭密封锥面，切断燃油回路，从而在泵腔内建立起燃油喷射所需的高压；断电后，复位弹簧迫使衔铁推动控制阀杆复位，开启密封锥面，卸载高压燃油，停止燃油喷射。该方式实现了对燃油喷射过程的数字控制，改变了传统喷油泵复杂的机械控制方式，通过调节控制阀杆的闭合时间和闭合时刻，可实现对循环喷油量和喷油定时的灵活控制。

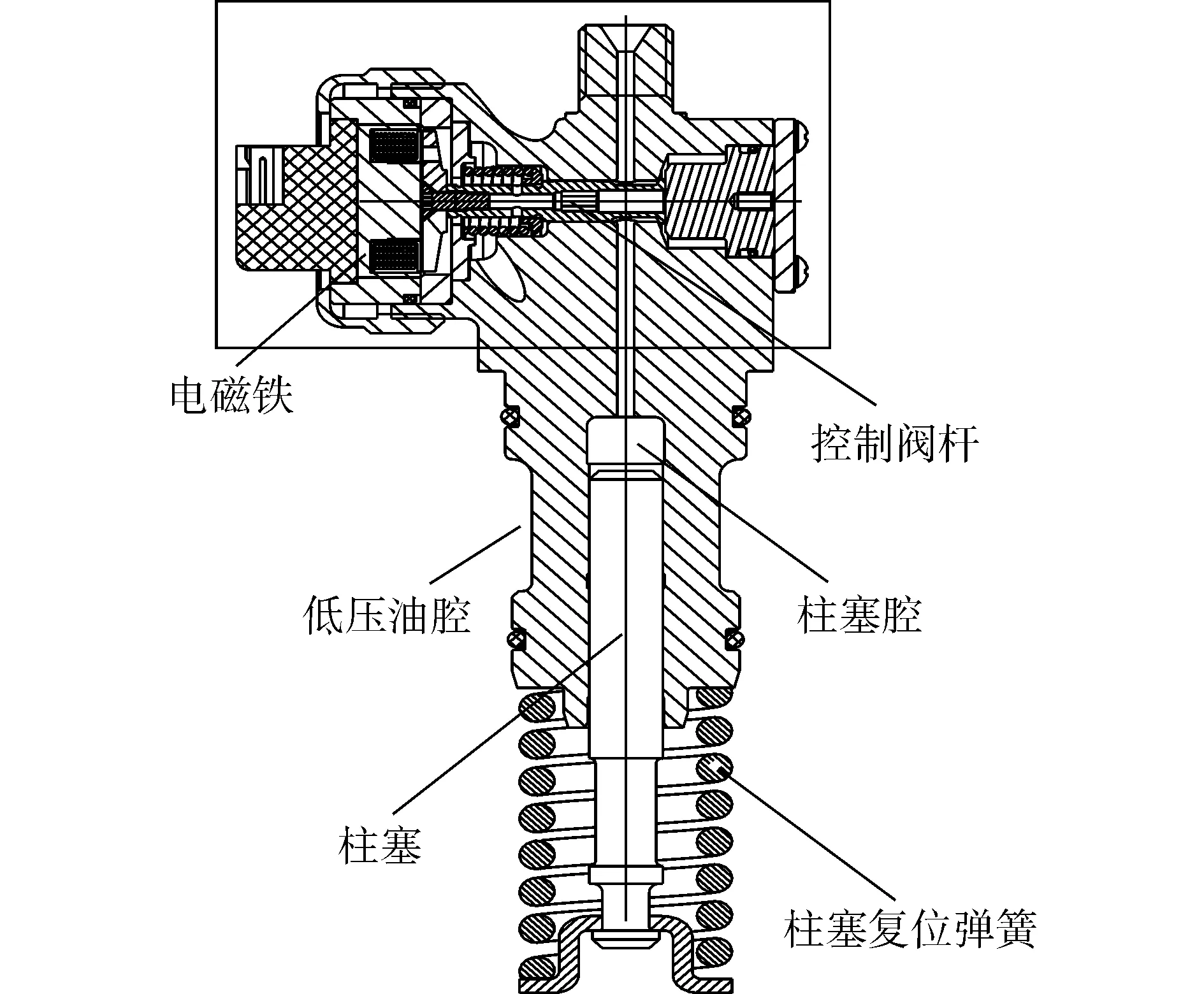
(a)电控单体泵结构

(b)电磁阀结构图1 电控单体泵、电磁阀结结构图Fig.1 Structure of EUP and solenoid valve

1.2 电磁阀响应延迟特性

在电磁阀关闭和开启阶段，由于电流作用时间、磁滞现象、阀杆动作延迟、阀杆运动过程等因素导致衔铁相对于控制电流(信号)存在滞后所产生的延迟时间。在电磁阀开启阶段由于较高压力的燃油迅速泄压，在燃油流经处会产生局部压降现象，使得燃油会对锥阀产生与开启方向相反的液动力，从而导致开启延迟时间增加。

根据衔铁受电磁力作用过程，可以将电磁阀的运动过程分为3个阶段(如图2所示)：

1) 关闭延迟阶段A：线圈通电起始时间到衔铁完全吸合时间即电磁阀到达最大升程时间。

2) 关闭阶段C。衔铁被吸合后，与电磁铁间隙较小，电磁力一直大于弹簧力，电磁阀保持完全关闭状态。

3) 开启延迟阶段B。电磁阀断电时间到衔铁复位即电磁阀完全打开时间。

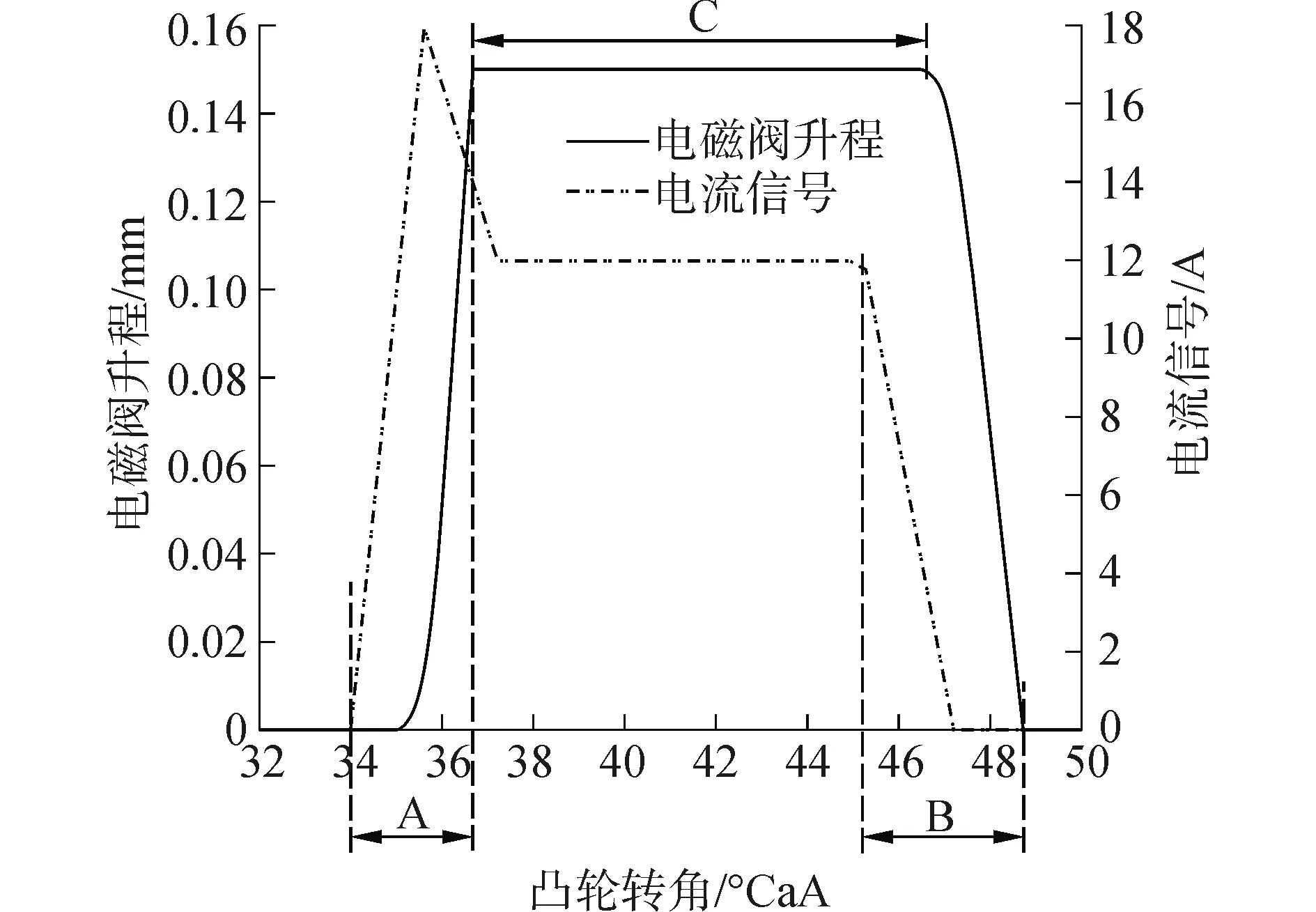
图2 电磁阀响应延迟特性Fig.2 Response delay characteristic of solenoid valve

2 仿真模型

电控单体泵系统是集电场、磁场、机械运动和流场于一体的复杂系统，各物理场通过各自的控制方程及相互作用变量耦合在一起，每个场的参数都会直接或间接的影响最终的喷射特性。单纯的实验研究难以实现对系统喷射特性的深入分析，需采用数值仿真的方法，以揭示影响喷射特性的本质规律。因此，本文在AMESim环境中建立了数值模型，如图3所示。

为验证模型的准确性，图4中(a)是凸轮转速为900 r/min，循环喷油量为150 mm3时，在相同控制电流下，喷油规律的实验和仿真结果对比曲线。

(a)电控单体泵仿真模型

(b)电磁阀仿真模型图3 电控单体泵及电磁阀仿真模型Fig.3 Simulation model of EUP and solenoid valve

图4(b)是在不同凸轮转速下，满足实验和仿真相同循环喷油量(某种机型外特性下循环喷油量)的前提下，泵端压力和嘴端压力的实验和仿真结果。可见仿真模型能够准确的预测泵端压力、嘴端压力和喷油规律，由图中可知系统在喷油过程中的燃油喷射持续期和喷油提前角是一致的，喷油时序也是一致的，而且在任何转速下泵端压力和嘴端压力都能得到很好的预测，最大偏差为7%，因此该模型能够准确预测系统的喷射特性参数[6]。

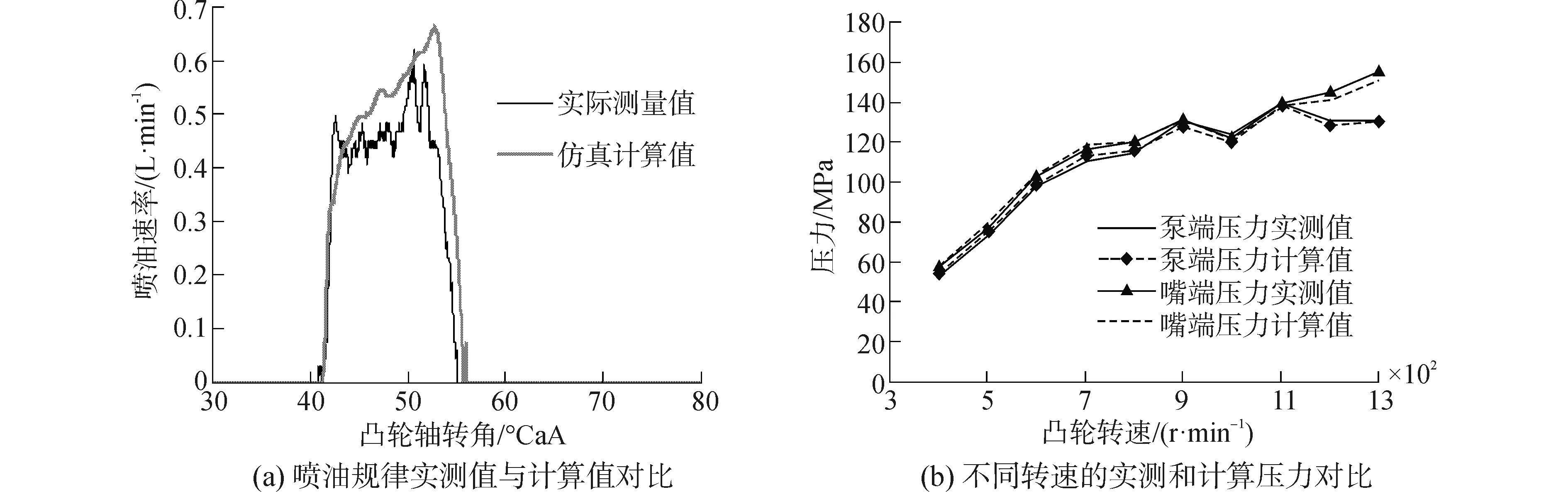
图4 实验与仿真计算对比Fig.4 Comparison between experiment and simulation

3 电磁阀响应延迟时间相关性预测

电磁阀部分的特性参数会影响电磁阀的响应延迟特性，为筛选关键因素，在保持控制策略及电磁阀固有物性参数如升程、质量和材质不变的前提下，选取了如表1所示的影响参数对电磁阀响应延迟经行了相关性预测分析，其中表1中参数基准值是实际测量值，取值范围是在不影响电控单体泵及电磁阀等各部分正常工作所允许的波动范围。

表1 电磁阀特性参数及取值范围

Table 1 Characteristic parameters and range of electromagnetic valve

参数基准值取值范围弹簧预紧力/N7050～90阻尼/(N·(m·s-1)-1)500～120锥阀半锥角/(°)6856～80衔铁残余气隙/mm0.120.08～0.15阀杆直径/mm5.55～6锥阀直径/mm7.67.5～8.2阀杆孔径/mm76.3～7.3电磁阀容积腔/mm30.410.3～0.5弹簧刚度/(N·m-1)100008000～12000

相关性分析是考察两个变量之间线性关系的一种分析方法，即，当一个变量发生变化时，另一变量随之如何变化，此时需要通过计算相关系数来做深入的定量考察。相关性分析需要从两方面来考察两变量间的线性关系，一是相关的强度，二是相关的方向。

设两变量有如下两组观测值：X：x1，x2，…，xn；Y：y1，y2，…，yn，则

(1)

式中：r即为变量X与Y的相关系数，r的取值范围为-1≤r≤1。相关系数的绝对值大小(即|r|)表示两变量直间的线性相关强度，相关系数r的正负表示相关的方向，r为正数，表示两变量间为正相关；r为负数，表示两变量间为负相关。

典型工况(凸轮转速为900 r/min，喷油脉宽为8°CaA凸轮轴转角)下，应用试验设计的思想，在MODDE环境下采取面中央合成设计(central composite face， CCF)的响应面(response surface modeling， RSM)方法，将各影响因素作为自变量，将电磁阀响应延迟时间作为响应变量，对各特性参数与电磁阀开启和关闭延迟时间的相关性进行了分析。

如图5所示，特性参数对电磁阀关闭延迟时间都是正相关的，说明关闭延迟时间随特性参数增大而增加；弹簧预紧力、残余气隙为、阻尼、锥阀直径相关系数分别为0.55、0.50、0.42、0.33，表明这些参数会对关闭延迟时间影响较大。而对于开启延迟时间，阻尼、阀杆直径、弹簧刚度、电磁阀容积腔是正相关的，说明开启延迟时间随这些特性参数增大而增加；其余是负相关，说明开启延迟时间随这些特性参数增大而减小。其中弹簧预紧力、锥阀半锥角、阻尼、阀杆直径相关系数分别为-0.67、-0.5、0.38、0.33，表明该些参数会对开启延迟时间影响较大；电磁阀容积腔、弹簧刚度与关闭延迟时间的相关系数分别为0.039、0.036，对开启延迟时间相关系数分别为0.018、0.014，表明它们对电磁阀响应影响微弱。其中阻尼是由于燃油的粘滞性、流动性及机械偶件之间相互摩擦所导致，即使对电磁阀响应延迟影响较大，但在优化设计中无法将其设计到最小。综上所述，本文选取优化的关键特性参数：衔铁残余气隙、弹簧预紧力、锥阀半锥角、阀杆直径及锥阀直径。

注：D1为阀杆孔径，D2为锥阀直径，D3为阀杆直径，d为阻尼，Y为柱塞弹簧预紧力，J为锥阀半锥角，R为衔铁残余气隙，S为柱塞弹簧刚度，V为电磁阀容积腔图5 各因素与电磁阀延迟响应相关性Fig.5 Correlation between the factors and the delay response

4 电磁阀响应延迟多目标优化

4.1 NSGA-II遗传算法

NSGA-II[5，7-11]是一种精英策略非支配排序遗传算法，在NSGA的基础上加上了精英策略、密度值估计策略和快速非支配排序策略。其优点是：计算复杂性从O(mN3)降至O(Mn2)，其中，m表示目标函数的数目、N表示种群中个体的数目；具有最优保留机制并且不需要确定一个共享参数；提高了算法的收敛性。NSGA-II算法得到的非劣解分布均匀，收敛性好，已经成为进化多目标优化领域的基准算法之一。

NSGA-II算法流程如图6[12]所示。

图6 NSGA-II算法流程图Fig.6 Flow chart of NSGA-II algorithm

4.2 多目标优化数学模型

本文优化目标为开启延迟时间fopen(x)和关闭延迟时间fclose(x)两个函数值最小时对应的x值，优化的关键特性参数：锥阀直径D1、阀杆直径D2、弹簧预紧力Y、锥阀半锥角J、衔铁残余气隙R，则电磁阀响应延迟的优化目标函数用数学描述为

Minimizefopen(x)

Minimizefclose(x)

根据设计中对各参数的选取范围，确定了各关键特性参数的约束条件：7.5≤D1≤8.2；5≤D2≤6；50≤Y≤90；56≤J≤80；0.08≤R≤0.15，fi(x)为第i(i=1，2，…，n)个目标函数，其中x为关键特性参数，x=(D1，D2，Y，J，R)T。

最终优化目标的解：取得出解集中离原点距离最近的点为最优集，即

(2)

式中：x0=(D10，D20，Y0，J0，R0)T为多目标优化结果。

4.3 多目标优化模型

图7所示为多目标优化平台modeFRONTIER与AMESim联合仿真模型，首先实验设计随机产生输入变量的相互组合，即赋予遗传算法初始值，经过AMESim计算得出输出变量的值，优化算法再根据目标函数的要求进行选择优化参数的变异和交换等操作，从而达到优化目的。本研究共有5个输入变量，电控单体泵在典型工况下进行仿真，将开启、关闭延迟时间作为输出变量，并将开启、关闭延迟时间最小作为最终优化目标。

4.4 多目标优化结果分析

图8(a)所示为电磁阀响应延迟时间多目标优化解集，从中选取符合电磁阀开启、关闭延迟时间都最小的Pareto最优解集前沿，如图8(b)所示，在Pareto前沿上选取满足优化目标的点，点A为优化前电磁阀响应延迟时间点，点C为关闭延迟最小点，点D为开启延迟最小点，但这两个点的参数配置均只能实现对单个目标的优化，为了同时实现对电磁阀开启和关闭延迟时间优化的目标，应用式(2)计算出d最小值的x0点，即点B作为最终优化结果点。

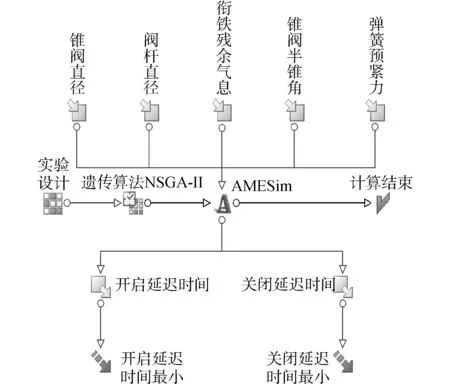
图7 电控单体泵多目标优化模型Fig.7 Multi-objective optimization model of EUP

从优化结果中可看出，表2给出了优化前后设计参数对比值，表3所示为优化前后电磁阀关闭延迟时间和开启延迟时间。优化后，关闭延迟时间减小了6%，开启延迟时间减小了17.7%，循环喷油量减小了1.50 mm3，喷油压力峰值增加

0.63 MPa。说明经过电磁阀延迟响应多目标优化，随着电磁阀响应的加快，喷油压力有所增加，对循环喷油量的控制也更加精确，可进一步改善电控单体泵的喷射特性。

图9给出了电磁阀优化前后电磁阀升程的对比，从图8(b)中可以看出，优化后的电磁阀开启时间提前了0.621°CaA凸轮轴转角即0.115 ms，电磁阀关闭时间早于优化前0.162°CaA凸轮轴转角即0.03 ms，响应速度快于优化前。

表2 优化前后参数对比

Table 2 Comparison of parameters before and after optimization

参数优化前优化后锥阀直径/mm7.608.20阀杆直径/mm5.505.55衔铁残余气隙/mm0.120.08锥阀半锥角/(°)68.0080.00弹簧预紧力/N70.0088.00

表3 优化前后结果对比

Table 3 Comparison of results before and after optimization

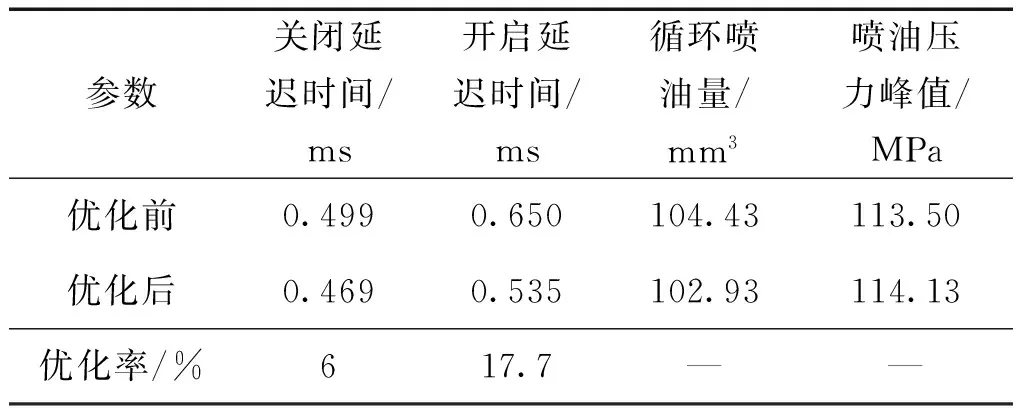
参数关闭延迟时间/ms开启延迟时间/ms循环喷油量/mm3喷油压力峰值/MPa优化前0.4990.650104.43113.50优化后0.4690.535102.93114.13优化率/%617.7——

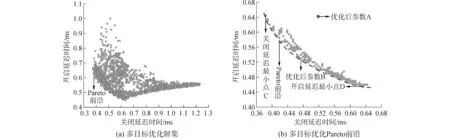
图8 多目标优化结果Fig.8 Multi-objective optimization results

优化前后电控单体泵的喷油压力及喷油速率对比如图10和图11所示，由于优化后，电磁阀关闭延迟时间减小，关闭时间提前，从而导致喷油时刻提前，优化后的喷油压力及喷油速率在同一凸轮转角时高于优化前。当喷油压力和喷油速率到达最大值后，由于电磁阀开启延迟时间减小，开启时间提前，燃油泄压速度加快，从而喷油压力和喷油速率迅速降低，更有利于循环喷油量的精确控制。

图9 优化前后电磁阀升程对比Fig.9 Comparison of solenoid valve lift before and after optimization

图10 优化前后喷油压力对比Fig.10 Comparison of injection pressure before and after optimization

图11 优化前后喷油速率对比Fig.11 Comparison of fuel injection rate before and after optimization

5 结论

1)应用实验设计方法，通过对电磁阀延迟响应因素的相关性分析，得出电磁阀延迟响应关键因素：衔铁残余气隙、弹簧预紧力、锥阀半锥角、锥阀直径、阀杆直径及其阻尼。

2)采用多目标优化算法NSGA-II对电控单体泵电磁阀响应特性进行了优化，优化结果表明：关闭延迟时间减小了6%，关闭时间提前，喷油压力及喷油速率在同一凸轮转角时高于优化前。

3)经过优化后，开启延迟时间减小了17.7%。开启时间提前，燃油泄压速度加快，喷油压力和喷油速率迅速降低，更有利于循环喷油量的精确控制。

[1]MULEMANE A， HAN Joongsub， LU Paihsiu， et al. Modeling dynamic behavior of diesel fuel injection systems[C]//SAE Paper， 2004-01-0536， 2004.

[2]FAN L Y， MA X Z， TIAN B Q， et al. Quantitative analysis on cycle fuel injection quantity fluctuation of diesel engine electronic in-line pump system[C]//SAE Paper， 2010-01-0875， 2010.

[3]张奇，张科勋，李建秋，等. 电控柴油机电磁阀驱动电路优化设计[J]. 内燃机工程， 2005， 26(2): 1-4.

ZHANG Qi， ZHANG Kexun， LI Jianqiu， et al. Optimization design of solenoid drive circuit for electronically controlled diesel engine [J]. Chinese internal combustion engine engineering， 2005， 26(2): 1-4.

[4]张廷羽，张国贤. 高速开关电磁阀的性能分析及优化研究[J]. 机床与液压， 2006 (9): 139-142.

ZHANG Tingyu， ZHANG Guoxian. Performance analysis and optimization of high speed solenoid valve [J]. Machine tool & hydraulics， 2006 (9): 139-142.

[5]范立云， 田丙奇， 马修真，等. 电控单体泵喷射特性关键影响因素研究[J]. 农业机械学报， 2011， (09): 20-26.

FAN Liyun， TIAN Bingqi， MA Xiuzhen， et al. Key influence factors investigation on the electronic unit pump injection characteristics[J]. Transactions of the Chinese society of agricultural machinery， 2011(9): 20-26.

[6]DEB K， PBATAP A， AGARWAL S. A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J]. IEEE transactions on evolutionary computation， 2002， 6(2): 182-197.

[7]JIANG Wenying， LIN Yan， CHEN Ming， et al. An ant colony optimization-genetic algorithm approach for ship pipe route design[J]. International shipbuilding progress， 2014 (3/4).

[8]GIAGKIOZIS I， FLEMING P J. Methods for multi-objective optimization: an analysis[J]. Information sciences， 2015.

[9]SUI Haiteng， NIU Wentie， NIU Yaxiao， et al. Pipe-assembly approach for ships using modified NSGA-Ⅱ algorithm[J]. Computer aided drafting， design and manufacturing， 2016(2): 34-42.

[10]LIU H， GU F. A improved NSGA-II algorithm based on sub-regional search[C]//Evolutionary computation 2011， “CEC”11. New Orleans， USA， 2011.

[11]DEB K， AGRAWAL S， PRATAP A， et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II[C]//Parallel problem solving from nature. Berlin， Germany: Springer-Verlag， 2000: 849-858.

[12]杜海峰.基于DE和NSGA-II的进化多目标优化算法及应用[D]． 西安：西安电子科技大学， 2012.

DU Haifeng. Evolutionary multi-objective optimization algorithm and its application based on DE and NSGA-II[D]． Xi′an: Xidian University， 2012.

[13]DHANALAKSHMI S， KANNAN S， MAHADEVAN K， et al. Application of modified NSGA-II algorithm to combined economic and emission dispatch problem[J]. International journal of electrical power and energy systems， 2011， 33(4): 992-1002.

[14]LI An′da， HE Zhen， ZHANG Yang. Bi-objective variable selection for key quality characteristics selection based on a modified NSGA-II and the ideal point method[J]. Computers in industry， 2016， 82: 95-103.

[15]NAJMEH A， SEYED M M， RAJA A R G， et al. Application of the NSGA-II algorithm to a multi-period inventory-redundancy allocation problem in a series-parallel system[J]. Reliability engineering and system safety， 2016，160: 1-10.

[16]VO-DUY T， DUONG-GIA D， HO-HUU V， et al. Multi-objective optimization of laminated composite beam structures using NSGA-II algorithm[J]. Composite structures， 2017，168: 498-509.

[17]LIANG Xiaozhen， YAN Guangrong， CHU Hongzen. A research on optimization of cutting parameters based on NSGA-II[J]. Advanced materials research， 2014， 936: 1687-1693.

[18]LI Hongtao， NIU Wentie， FU Shengli， et al. Multiobjective optimization of steering mechanism for rotary steering system using modified NSGA-II and fuzzy set theory[J]. Mathematical problems in engineering， 2015(1): 1-13.

Multi-objective optimization analysis of a high speed solenoid valve for an electronic unit pump

ZHANG Jianyu1，FAN Liyun2，YUAN Hang1

(1.The Sixth Department， 713 Research Institute of China Shipbuilding Industry Corporation， Zhengzhou 450052， China; 2.Department of Power and Energy Engineering， Harbin Engineering University， Harbin 150001， China)

Delayed response in high-speed solenoid valves will cause fuel injection timing misalignment and lower accuracy of cyclic fuel injection quantity. This problem results in an increase in fuel consumption and diesel engine exhaust emissions. This paper demonstrates， through multi-objective analysis and optimization of the electromagnetic valve structure， that minimizing the response delay of the valve is achievable. This paper establishes a simulation model of the electronic unit pump using AMESim software. It is proved by the experiment model accuracy. The key parameters influencing the solenoid valve response delay are predicted by the method of experimental design. The key parameters are residual air gap， spring preload， half angle of the poppet valve， the diameter of the valve rod， and the diameter of the poppet valve. Used the modeFRONTIER multi-objective multidisciplinary optimization application platform and the NSGA-Ⅱ genetic algorithm， the opening and closing response delay time as a target of multi-objective optimization， the model of electronic unit pump high-speed solenoid valve is set up. The optimized results indicate the delay time of closing the solenoid valve is reduced by 6%， the delay time of opening the solenoid valve is reduced by 17.7%， and the injection pressure peak is increased by 0.62 MPa， which improve the accuracy of the cyclic fuel injection quantity.

electronic unit pump; high-speed solenoid valve; multi-objective optimization; AMESim; response delay; modeFRONTIER; diesel engine; emission; fuel injection quantity

2016-04-26.

日期：2017-03-17.

张建宇(1987-)， 男， 助理工程师; 范立云(1981-)，男，教授，博士生导师.

张建宇， E-mail:zhjyu321@126.com.

10.11990/jheu.201604065

TK423

A

1006-7043(2017)04-0561-08

张建宇，范立云，袁航.电控单体泵高速电磁阀多目标优化分析[J]. 哈尔滨工程大学学报， 2017， 38(4): 561-568.

ZHANG Jianyu，FAN Liyun，YUAN Hang.Multi-objective optimization analysis of a high speed solenoid valve for an electronic unit pump[J].Journal of Harbin Engineering University， 2017， 38(4): 561-568.

网络出版地址：http://kns.cnki.net/kcms/detail/23.1390.u.20170317.0858.012.html