中考中扇环问题分析

董月红

中考中扇环问题分析

董月红

在两个同心圆中，任作两条半径，它们与圆相交，形成的四边形我们称为扇环，如图1阴影部分.近年来，扇环问题频频出现在中考中.有面积问题，弧长问题等，这类中考题大多以现实生活为背景，经常与解直角三角形、方程（组）综合在一起.对于求阴影面积的有关考题，常用的方法有：直接应用公式法，和差法，割补法等.

图1

例1（2005·山西）图2是一纸杯，它的母线AC和EF延长后形成的立体图形是圆锥.该圆锥的侧面展开图是扇形OAB.经测量，纸杯上开口圆的直径为6cm，下底面直径为4cm，母线长EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积.（图形计算结果用π表示）

图2

即扇形OAB的圆心角是45°.

∵R=24，∴R-8=16.

∴S扇形OCD=

S扇形OAB=

S纸杯侧面积=72π-32π=40π.

S纸杯底面积=π×22=4π，从而S纸杯表面积=44π.

【评析】对由多部分构成的面积问题，需先明确要计算哪一部分的面积，它可通过哪些图形进行分割或拼凑而得到.

例2（2016·黄石）如图3所示，正方形ABCD对角线AC所在直线上有一点O，OA= AC=2，将正方形绕O点顺时针旋转60°，在旋转过程中，正方形扫过的面积是.

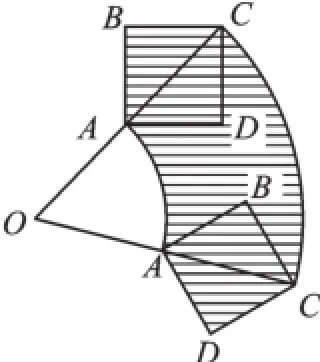
图3

【分析】如图3，正方形绕O点顺时针旋转60°，所扫过的图形是扇环的面积再加上正方形ABCD的面积.

解：∵OA=AC=2，

∴AB=BC=CD=AD=2，OC=4，

S阴影=

故答案为：2π+2.

【点评】此题考查了扇形的面积公式、旋转的性质以及勾股定理，能够把不规则图形的面积转换为规则图形的面积是解答此题的关键.

例3（2015·宜宾）如图4，以点O为圆心的20个同心圆，它们的半径从小到大依次是1、2、3、4、……、20，阴影部分是由第1个圆和第2个圆，第3个圆和第4个圆，……，第19个圆和第20个圆形成的所有圆环，则阴影部分的面积为（）.

A.231πB.210πC.190πD.171π

【分析】根据题意求出各个圆环的面积，进而求出它们的和.

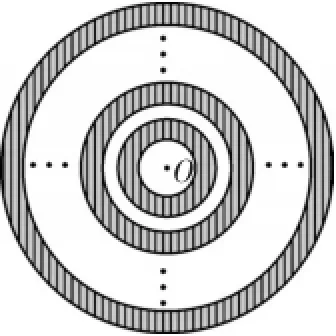
图4

解：由题意知，阴影部分的面积为π（22-12）+π（42-32）+π（62-52）+…+π（202-192）=π（3+7+ 11+15+…+39）=π·5（3+39）=210π，选B.

【点评】本题考查了平方差公式，求自然数和等知识.

例4（2016·福田二模）如图5，⊙O的半径为︵2，AB，CD是互相垂直的两条直径，点P是上一点，过点P作PM⊥AB于点M，PN⊥CD于点N，点Q是MN的中点，当点P从点A沿转动到点D处时，线段PQ扫过的面积为.

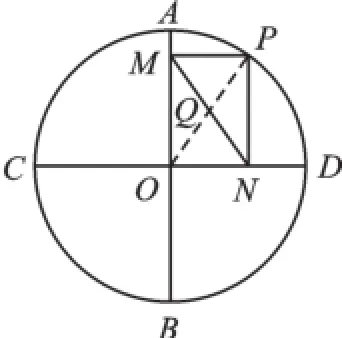
图5

【分析】矩形的对角线相等且互相平分，即MN=OP=2，OQ=1，点P从点A沿︵转动到点D处时，转动的圆心角为90°，线段PQ扫过的面积是圆心角为90°的扇环.解：连接OP，由矩形性质知：OP=MN，且它们相交于中点Q，则当点P从点A沿︵转动到点D处时，转动的图形是90°扇环.线段PQ扫过的面积为

【评析】解题的关键是要明确点Q运动的路线是以O为圆心，以1为半径，圆心角为90°的扇形；点P运动的路线是以O为圆心，以2为半径，圆心角等于90°的扇形.所以线段PQ运动的路线是以O为圆心的扇环.

例5（2015·乐山）如图6，已知A（2 3，2）、B（2 3，1），将△AOB绕着点O逆时针旋转，使点A旋转到点A′（-2，2 3）的位置，则图中阴影部分的面积为.

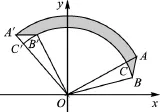
图6

【分析】设以O为圆心，以OB为半径的圆交OA于C，交OA′于C′，则曲边形ABC的面积等于曲边形A′B′C′的面积，所以阴影部分的面积等于扇环的面积..

∵由A（2 3，2）旋转到点A′（-2，2 3），

∴∠A′OA=∠B′OB=90°，根据旋转的性质可得，S曲边形ABC=S曲边形A′B′C′，∴阴影部分的面积等

【评析】利用分割法将不规则的图形转化成规则的图形，由条件A、A′的坐标求出∠AOA′的度数为90°是解决问题的关键.

（作者单位：江苏省丰县初级中学）