基于改进MTGS的资源管控预案评估指标赋权算法

段艳红， 丁建江， 许红波， 周 芬

(1. 空军预警学院空天预警实验室， 湖北 武汉 430019； 2. 95333部队， 湖南 长沙 410114)

基于改进MTGS的资源管控预案评估指标赋权算法

段艳红1,2， 丁建江1， 许红波1， 周 芬1

(1. 空军预警学院空天预警实验室， 湖北 武汉 430019； 2. 95333部队， 湖南 长沙 410114)

针对决策者确定评估指标权重存在主观偏好这一问题,提出了基于灰靶贡献度排序和田口施密特正交(Mahalanobis-Taguchi Gram-Schmidt,MTGS)的指标赋权算法。该算法在MTGS系统方法中结合灰色系统技术，直接从评估指标数据入手，并通过计算指标灰靶贡献度得出了指标重要性排序结果；依据排序结果,构造了新的评估指标矩阵，有效地避免了人为因素对指标权重结果的影响。最后，以某传感器组网系统的体系抗干扰资源管控预案评估为例，通过与熵值客观赋权算法的结果进行对比验证了该算法的可靠性。

灰靶贡献度； 传感器组网； 资源管控预案评估； 田口施密特正交； 指标赋权算法

在传感器组网资源管控预案评估中，指标权重分配一直是影响评估结果可信度的难点问题。若要确定各因素对评估结果影响程度的权重，则需考虑指标本身的特性价值、决策者的主观偏好和评估方法的选择等多种因素。当前，确定评估指标权重的研究成果主要分为2类。一类研究成果是主观定权算法，DOYLE等[1]提出了专家对指标重要度进行百分制打分的分值分配方法(Point Allocation Method，PAM)。KOK等[2]通过引入比率标度，提出了一种由专家对指标相对重要程度进行判断的两两比较方法(Pairwise Comparisons Method，PCM)，该方法的经典运用是美国SAATY教授[3]提出的层次分析法(Analytic Hierarchy Process，AHP)。为了避免专家在进行打分或两两比较时的感知差异，产生了另一种通过专家按指标相对重要性排序的秩排序方法(Rank Ordering Method，ROM)[4]，该方法又分为秩分布(Rank Order Distribution，ROD)算法[5]和秩心(Rank Order Centroid，ROC)算法[6]等。这些主观定权算法可能由于人为主观因素，往往会造成评估结果的偏差。另一类研究成果是客观定权算法，具有代表性的是熵值客观权重算法(Entropy Objective Weights Algorithm，EOWA)[7]和离差最大化算法[8]。由此可见：确定评估指标权重多采用传统的定性算法，定量研究相对较少。然而，由于确定评估指标权重所依赖信息的“隐蔽性”和“关联性”导致确定评估指标权重的“灰色性”，采用上述传统的定性算法衡量指标重要性易受人为因素干扰，无法满足科学性和客观性要求，其应用范围受到一定的限制，而且无法评估指标的关联性。因此，笔者提出一种改进田口施密特正交(Mahalanobis-Taguchi Gram-Schmidt，MTGS)系统的指标赋权算法，并以某传感器组网系统的体系抗干扰资源管控预案评估为例，验证该算法的有效性。

1 算法基本原理

综合评估的主要目的是根据多个指标对备选预案的优劣比较结果进行排序,为此，各指标权重的确定需考虑指标数值属性的差异和相对重要性，因此需借助模式识别技术来准确地反映多个指标数值组成的不同备选预案的差异程度。TAGUCHI等[9]提出的系统方法为解决该问题提供了很好的借鉴，但该方法在对指标相对重要性进行排序时依然无法避免人为主观因素的影响。为了解决这一问题，王正新等[10]对灰色系统理论[11]中的灰靶技术进行了改进：首先，灰靶技术采用最能反映各个不同预案综合效果的性能数据指标，通过灰靶构成与各个不同预案所对应的数据模式，标准模式是灰靶的靶心，远离靶心的模式称之为靶界，向下远离者称之为下靶界，向上远离者称之为上靶界；其次，由灰靶变换得到各指标的灰靶贡献度值，依据该值大小，可得指标相对重要性比较结果；最后，与MTGS系统相结合，实现对指标权重的计算。基于改进MTGS的指标赋权法基本原理如图1所示。

图1 基于改进MTGS的指标赋权法基本原理

2 算法模型

在评估多个备选预案时，将参与评估的某一预案作为预案评估比较这一命题的灰模式，设为ωk，k∈{1,2,…,m}，其中，k为预案的序数，m为所选预案的数量；设ω(i)为指标序列向量，i∈{1，2，…，n}，其中，i为指标的序数，n为所选指标的数量。基于改进MTGS的指标赋权算法流程如图2所示。

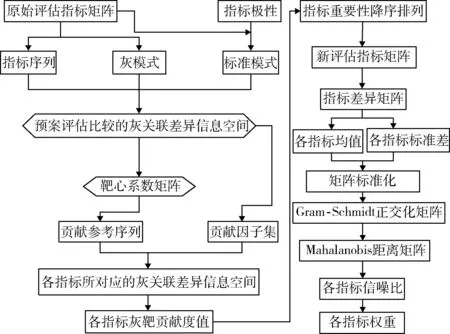
图2 基于改进MTGS的指标赋权算法流程

2.1 评估指标体系

假设现有m个待评估的不同预案组成备选评估集，有n个评估因素组成预案评估指标集，则可构造评估指标矩阵：

X=[xki]m×n。

(1)

式中：xki为第k个预案在第i个评估指标的值。

结合文献[12-13],笔者建立了预案评估指标体系，预案评估指标极性及含义如表1所示，该评估指标体系可以根据需要适当地进行调整和扩充。

表1 预案评估指标极性及含义

2.2 基于灰靶贡献度的指标重要性排序模型

根据建立的预案评估指标体系，基于灰靶贡献度的指标重要性排序模型建立步骤如下：

1)确定标准模式。设ω0为标准模式向量，ωk(i)为第k(k=1,2,…,m)个预案的第i个评估指标数值，ω0(i)为第i个评估指标的标准模式值。对于第i个指标序列向量ω(i)，不同的指标存在极大值极性、极小值极性和适中值极性。在确定标准模式时：

若ω(i)存在极大值极性，则ω0(i)=max(ωk(i));

若ω(i)存在极小值极性，则ω0(i)=min(ωk(i));

若ω(i)存在适中值极性，则ω0(i)=avg(ωk(i))。

2)确定预案评估比较的灰关联差异信息空间δPR。若Ψ为灰靶变换，由于不同的指标序列存在不同的极性，传统的灰靶变换难以完全满足指标极性多样性的要求，因此笔者采用改进型灰靶变换Ψ[14]，则有

Ψωk(i)=

(2)

如果Ψω0=x0，且x0={x0(1),x0(2),…,x0(n)}={ω0(1),ω0(2),…,ω0(n)}，则称x0为标准靶心，简称靶心。

则可确定预案评估比较的灰关联差异信息空间为

δPR=(δ,τ,δ0k(max),δ0k(min))。

(3)

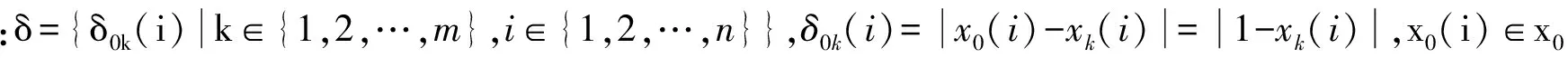
3)确定单一指标的靶心系数。为了解决灰靶贡献度的不确定性，需要合理选取贡献参考序列和确定贡献因子集。为此，需要确定指标的靶心系数。设γ(x0(i),xk(i))为第i个评估指标的靶心系数，其计算方法为

(4)

4)确定贡献参考序列和贡献因子集。为了解决因灰靶贡献度的不确定性而导致的指标重要性排序不合理问题，确定贡献参考序列和贡献因子集[15]分别如下：

(5)

Φωi(k)=1-δ0k(i)。

(6)

5)确定各指标所对应的灰关联差异信息空间。根据灰靶理论，各指标所对应的灰关联差异信息空间可表示为

ΩIR=(Ω,τ,Ω0i(max),Ω0i(min))，

(7)

6)确定单一指标的灰靶贡献度值。由于单一指标的灰靶贡献度值由单一指标的贡献系数的平均和得到，为此，需要确定单一指标的贡献系数。设η(x0(k),xi(k))为第i个评估指标的贡献系数，其计算方法为

(8)

则单一指标的灰靶贡献度值为

(9)

2.3 改进的MTGS指标赋权计算模型

改进的MTGS指标赋权计算模型建立步骤如下：

1)确定新的评估指标矩阵。按单一指标灰靶贡献度值由大到小的顺序，对指标重要性进行降序排列，得到G1,G2,…,Gn，变序后的新评估指标矩阵记为

(10)

2)确定指标差异矩阵。由变序后的新评估指标矩阵确定指标差异矩阵，记为

(11)

3)确定各指标均值和标准差。根据指标差异矩阵，可以确定各指标均值为

(12)

由指标差异矩阵和均值可得标准差为

(13)

4)新评估指标矩阵标准化。由各指标均值和标准差可确定标准化后的新评估指标矩阵为

(14)

5)新评估指标矩阵Gram-Schmidt正交化。为了消除各指标间的信息交叠，对矩阵E中各列向量进行Gram-Schmidt正交化[16]，其迭代公式为

(15)

正交化后由βi构成的矩阵记为

B=[βki]m×n，

(16)

式中：βki为B中第k个预案在第i个评估指标对应的元素。

6)确定正交化矩阵的Mahalanobis距离dki。正交化矩阵的Mahalanobis距离公式[9]为

(17)

式中： μ=(μ1,μ2,…,μn)T，为B中各列向量βi均值构成的向量；Σ-1表示对正交化矩阵中元素之间的协方差矩阵求逆运算。

7)确定各指标的信噪比。指标的信噪比用于度量该指标的稳健性程度，以此衡量各指标的权重。评估指标矩阵经过正交化处理后，其各指标的信噪比为

(18)

8)确定各指标的权重。各指标的信噪比经过归一化后即为各指标所对应的权重，其计算公式为

(19)

3 算法应用示例

以某传感器组网系统抗复杂电子干扰资源管控为例，对其资源管控的4个不同预案(即k=1,2,3,4)进行算法验证，以确定8个评估指标(i=1,2,…,8)的权重分配情况。结合实例和预案比较的评估指标体系，首先由专家定性分析并打分得出各评估指标数值，如表2所示，再运用算法模型进行赋权仿真计算。

应用MATLAB R2009b软件对该算法进行仿真计算，由式(3)可得预案评估比较的灰关联差异信息空间δPR(i)。各指标在不同预案上的灰关联差异信息值δ0k(i)如表3所示，从该表中可科学地反映出8个评估指标在4个不同预案上的灰关联差异信息值大小。

依据表3的灰关联差异信息值δ0k(i),可得δ0k(max)和δ0k(min)的值，再由式(4)可得靶心系数γ(x0(i),xk(i))，其计算结果如表4所示。

限于篇幅，以下只给出部分步骤的仿真结果。由式(9)可得各指标灰靶贡献度值，依据该值大小可得指标重要性排序，结果如表5所示。按照各指标重要性排序结果对原始评估指标矩阵的列向量重新进行调整，形成新的评估指标矩阵，再进入MTGS系统进行仿真。图3为预案评估指标的Mahalanobis距离分布。

表2 预案评估指标数值

表3 各指标在不同预案上的灰关联差异信息值δ0k(i)

表4 预案评估指标靶心系数计算值

表5 各指标灰靶贡献度和重要性排序

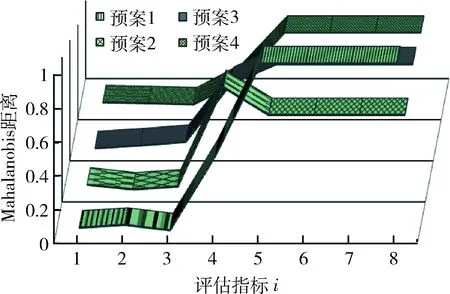
图3 预案评估指标的Mahalanobis距离分布

通过MTGS系统仿真，得到各指标信噪比和权重，结果如表6所示。可以看出：指标信噪比的大小决定了权重的大小，符合客观实际，弥补了传统主观定性分析方法造成的指标权重分配差异的不足。

为了验证本文算法的可靠性，利用经典的EOWA法[7]对本文实例进行仿真，EOWA法与本文算法仿真结果对比如图4所示。可以看出：本文算法与EOWA法的权重分配仿真结果基本一致，说明本文算法是可靠的。

表6 各指标信噪比和权重

图4 EOWA法与本文算法仿真结果对比

4 结论

笔者基于灰靶贡献度排序提出了一种改进的MTGS指标赋权算法，以某传感器组网系统的体系抗干扰资源管控预案评估为例进行了仿真计算，并与经典的EOWA法仿真计算结果进行了对比，结果表明：该算法是可靠的。该算法适用于管控预案评估指标权重计算，具有客观性和可操作性等优点，可解决预案评估中指标权重计算难的问题。下一步，该算法将用于资源管控预案工程化中的预案评估研究，为预案工程化应用提供参考依据。

[1] DOYLE J R,GREEN R H,BOTTOMLEY P A.Judging relative importance:direct rating and point allocation are not equivalent[J].Organizational behavior and human decision processes,1997,70(1):55-72.

[2] KOK M,LOOTSMA F A.Pairwise comparison methods in multiple objective programming[J].European journal of operational research,1985,22:46-55.

[3] SAATY T L.The analytical hierarchy process[M].New York:McGraw Hill,1980:49-52.

[4] JIA J,FISCHER G W,DYER J S.Attribute weighting methods

and decision quality in the presence of response error:a simulation study[J].Journal of behavioral decision making,1998,11(2):89-105.

[5] ROBERTS R,GOODWIN P.Weight approximations in multi-attribute decision models[J].Journal of multi-criteria decision analysis,2003,11(6):291-303.

[6] BARRON F H,BARRETT B E.Decision quality using ranked a-ttributes weights[J].Management Science,1996,42(11):1515-1523.

[7] 徐达,李闯,焦庆龙,等.基于主客观组合赋权的装甲装备维修性综合评价[J].装甲兵工程学院学报,2014,28(6):18-22.

[8] 李俊生,梁伟,刘雪梅,等.基于离差最大化的导弹中段目标威胁度评估[J].系统工程理论与实践,2007,27(5):164-167.

[9] TAGUCHI G,JUGULUM R.The Mahalanobis-Taguchi strategy:a pattern technology system[M].New York:John Wiley & Sons,2002:47-58.

[10] 王正新,党耀国,杨虎.改进的多目标灰靶决策方法[J].系统工程与电子技术,2009,31(11):2634-2636.

[11] 邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002:139-150.

[12] 李磊,王富章.基于改进多准则妥协解排序(VIKOR)法的铁路应急预案评估研究[J].中国安全科学学报,2012,22(8):29-36.

[13] 陈永光，李修和，沈阳.组网雷达作战能力分析与评估[M].北京:国防工业出版社,2006:40-56.

[14] 宋捷,党耀国,王正新,等.正负靶心灰靶决策模型[J].系统工程理论与实践,2010,30(10):1822-1827.

[15] 杨志良,薄玉成,白云,等.灰靶贡献度技术的改进与应用[J].火炮发射与控制学报,2006(3):23-26.

[16] YUEN S M,GERLACH K.Convergence properties of Gram-Schmidt and RLS adaptive algorithms[J].IEEE transactions on aerospace and electronic system,1990,19(7):44-56.

(责任编辑: 尚彩娟)

Evaluation Index Weight Algorithm of Resource Control Plan Based on Improved Mahalanobis-Taguchi Gram-Schmidt

DUAN Yan-hong1,2， DING Jian-jiang1， XU Hong-bo1， ZHOU Fen1

(1. Laboratory of Aerospace Early Warning, Air Force Early Warning Academy, Wuhan 430019, China; 2. Troop No.95333 of PLA, Changsha 410114, China)

Aiming at the problem that decision-maker has subjective misjudgment in determining evaluation index weight, a new index weight algorithm based on grey target contribution degree ranking and Mahalanobis-Taguchi Gram-Schmidt (MTGS) is proposed. The algorithm is combined with grey system technique in MTGS, makes a good use of the evaluation index data directly, and works out the index importance ranking result by calculating grey target contribution degree of each index. Then, according to the results of ranking, a new evaluation index matrix is constructed, and can effectively avoid human influence factors on the result of index weight. In the end, taking the system of systems anti-jamming resource control plan evaluation of a sensor networking system as an example, the reliability of the algorithm is ve-rified by comparing with the entropy objective weight algorithm.

grey target contribution degree; sensor networking; resource control plan evaluation; Mahalanobis-Taguchi Gram-Schmidt (MTGS); index weight algorithm

1672-1497(2017)02-0101-06

2016-09-18

国家自然科学基金青年科学基金资助项目(61401503)

段艳红(1982-)，男，博士研究生。

0159

A

10.3969/j.issn.1672-1497.2017.02.021