Direction of Arrivals Estimation for Correlated Broadband Radio Signals by MVDR Algorithm Using Wavelet

Ying Liu , Chi Xie Yourun Zhang

1 School of Energy Science and Engineering, University of Electronic Science and Technology of China, Chengdu, 611731, China

2 Department of Mechanical Engineering, Jincheng College of Sichuan University, Chengdu, 611731, China

3 School of Microelectronics and Solid-State Electronics, University of Electronic Science and Technology of China,Chengdu, 611731, China

* The corresponding author, email: yingliu56@hotmail.com

I. INTRODUCTION

With the high development of a smart antenna system, the physical characteristics of the network are also asked to be better processing the radio signals [1]. Independent component analysis is one of the techniques commonly used for the separation of sources from their mixtures which received from different directions, while it has a basic requirement that the number of mixtures available must be at least equal to the number of source signals. In [2],Bo fill et al. used a potential function method to estimate the mixing matrix and a geometry shortest path algorithm to achieve separation.When the sources are not sparse in the time domain, some algorithms for achieving the sparse in the transform domain are proposed,such as Fast Fourier Transforms. By utilizing sparsely in the time-frequency domain, many algorithms have been proposed for blind source separation of under determined instantaneous mixtures. In [3], degenerate un-mixing estimation technique was developed to solve the under determined source separation in the time-frequency domain, and Yilmaz and Rickard improved the estimation performance of sources by smoothing. If the source signals overlap to some degree in time-frequency domain a, the ratio of mixtures method [4] can be used to estimate the mixing matrix and source signals. However, these algorithms involve hyper parameters estimation process which requires high computational load. In fact, the modeling of complex communication/radar signals remains a difficult task. Hence, a single frequency Fourier transform is not suitable for signal analysis, instead, the time-frequency wavelet distribution is used.

The high resolution DOAs has been consid-erably interested by people too, and using the optimum pattern synthesis method has become very popular. There were several estimation methods available in the literature and the well known existing methods include subspace based method such as multiple signal classification(MUSIC) [5], estimation of signal parameters via rotational invariant techniques(ESPRIT) [6]. The minimum variance distortionless response (MVDR) spectrum estimator which provides an estimate of the power density spectrum over space field, and does not need to know the subspace rank like the MUSIC algorithm [7]. However, in the multipath radio environments, the performances of these methods are rapidly degraded because of the highly correlated relation. In [8],the DOAs is treat as a multi-calss classification statistics problem utilizing the support vector machine,which need solving the quadratic programming to get the support vector in DOAs estimation. In [9], the Toeplitz matrix is proposed by squaring the array covariance matrices, but the rank of it is only related to the DOAs of the signals and is not subjected to the signal coherence. So the subarray cross coherent was considered in [10], which yields a more stable estimation of the covariance matrix, whereas the angular resolution is enhanced by the spatial smoothing (SS). SS technique presents a satisfactory solution for the problem of narrowband correlated sources. A forward/backward spatial smoothing technique was adopted in [11,12], which can process more signals than the forward-only scheme. However, the number of resolved signals is limited to the number of array elements, and if the source signals do not overlap in the TF domain, high accuracy estimation could be obtained. But,in the practical field of communication signal processing, the assumption is rather restrictive and difficult to satisfy.

In this paper, the authors proposed the DOAs algorithm to cope with the correlated signals in wireless radio communication.

In this paper, the DOA estimation and SS problem are considered, and we propose a novel under-determined separation and DOA estimation algorithm in the TF domain under the assumption that the number of sources is less than that of sensors in each TF partition domain. The number of the signals needs not to be known as a prior and can be obtained along with the DOA estimation process. And the proposed algorithm provides a better performance in separating source signals than subspace method.

II. MVDR DIRECTION MODEL FOR NARROWBAND RADIO SIGNAL

Suppose N narrowband source signals impinge on M sensors, the complex envelops of the signals received by the array can be expressed by,

However, under the signals correlation condition, the R matrix is singular covariance matrix, and the optimal solution w can’t be obtained. In order to find signals correlated relation, the received signal covariance matrix introduced in [13] is:

The w is considered a bank of filter, at the output of MVDR algorithm filters, one wants to minimize the contribution of the signal subspace only the filter has the orthogonal relation character between the signal subspace and noise subspace. Nonetheless in practice,because of the limited sample data, the orthogonal relation can’t be precisely obtained,so the spectral peaks in MVDR algorithm will be peak position offset phenomenon or “false peak” phenomenon.

III. PROPOSED DIRECTION MODEL FOR BROADBAND RADIO SIGNAL

Space L2(R) can be orthogonal decomposed into a series of wavelet subspace sequences. And the decomposition of the signal x(t) into the orthogonal wavelet transformation is shown,

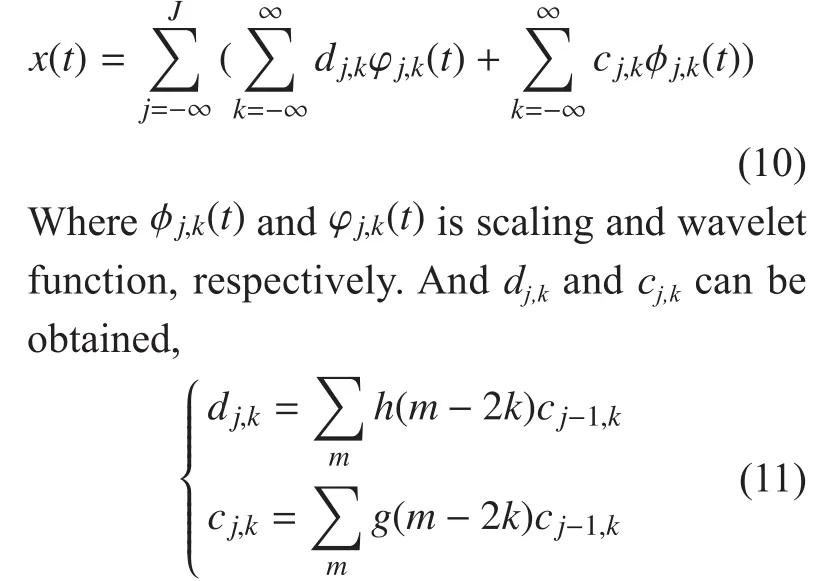
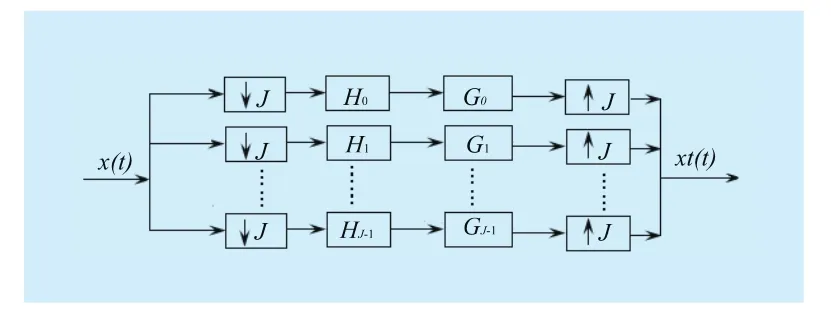
Fig. 1 The structure of J channel of wavelet filter banks

The scale factor and wavelet coefficients in j scale space can be obtained by weighted sum of wavelet filters h(k) and scale filters g(k) in j-1 scale space. The expansion coefficients cj,kis showing the “pro file” of the signal x(t), and the expansion coefficients dj,kis showing the“detail” of the signal x(t), and dj,kis wavelet coefficients. A block diagram of the wavelet filter banks is shown in Figure 1. In practice,the synthesis and analysis filter banks are implemented in discrete time, but we have also chosen to present them in terms of continuous time filters, because as this formulation can serve our discussion better.

Discrete orthogonal compactly supported by wavelets and the size is equal to or less than N, where N is an integer. J is the number of channel. H is a low pass filter with impulse response {hk} (-N/J≤k≤N/J) and G is a high pass filter with impulse response {gk} (-N/J≤k≤N/J). The impulse response of filer G is related to the impulse response of filter H by gk=(-1)1-kh1-k. The H and G are satisfied the PR (perfect reconstruction) condition. With the help of this decomposition, a very good time resolution is available at the high frequency, and a good frequency resolution can be also obtained at the low frequency. Because the scaling coefficients and wavelet coefficients of the j scale space can be gotten by weighted sum of filters h(k)and g(k) which has the 2k tap length under the j-1 scale space. Jthlevel wavelet decomposition corresponding matrix is shown in (12). (J is the decomposition levels)

The wavelet decomposition matrix can be expressed as following：

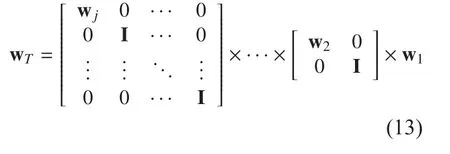
The signal is decomposed into the low-frequency component and high frequency components by the wavelet filter h(k) and scale filter g(k). In severe multipath propagation situation, the covariance matrix of every frequency has singular characteristic within received broadband signal, which is hard to effectively solve the source number and arrival angles information in the correlated signal subspace or the correlated noise subspace. After the wavelet transform, thechanged into the sparse matrix, and it has the orthogonal characteristic, where ‘a·b’ denotes element multiplication of a and b. Theis full rank of (9) as the new no singular covariance matrix in (6) to get the array weight vector. So, the correlated between the signals can be reduced and the speed of adaptive signal processing can be also improved greatly. The wideband signal is easily influenced by the mutipath and interference signal.

The preprocessed is needed to determine the frequency position of the desired signal and reduce the mutipath and interference influences. Therefore, the steps to implement the proposed algorithm can be described as follows.

IV. EXTENSION FOR CORRELATED SIGNALS

The performance of all algorithms gets severely degraded in the presence of correlated signals. The presence of constraints in the formulation allows the possibility of detecting signals and recursively forcing zeros in the spectrum, thus allowing several correlated signals to be detected. The first step of the recursion consists of running the above presented wavelet MVDR algorithm itself in order to detect as many signals as possible. Then, SS technique can be straightforwardly applied to the wavelet methods presented here. The signal bandwidth is divided into 2N groups by the wavelet packet, and each little group includes a number of frequencies, in which the number of frequency is J0. Then, the MVDR algorithm is designed to get the spatial spectrum of each frequency sub-band. Finally, we do the arithmetic average for the spatial spectrum in each group, and do the geometric mean for all groups to get the final spatial spectrum.

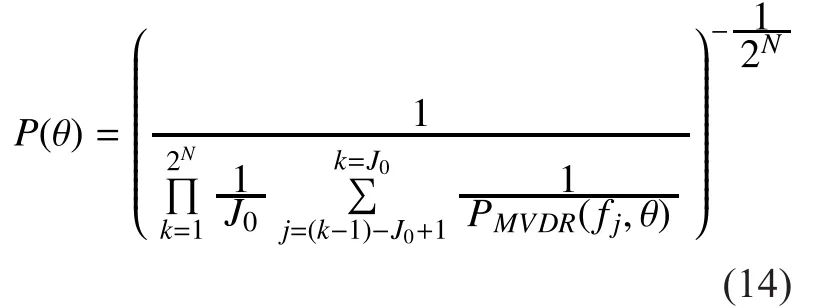
PMVDR(fj,θ) is the spectrum for the jthfre-quency of the MVDR algorithm. The spectrum peak with the number K can be obtained,when the wavelet MVDR algorithm is done inside the angle scanning of the array antenna system. This method consists of dividing the array into subarrays and performing the algorithm in each one of the subarrays, then averaging the estimated spectra. This method has its advantage. On the one hand, the SS methods reduce the spatial resolution of the estimation, and the number of subarrays needed to produce full rank autocorrelation matrices depends on the number of coherences in the signals. On the other hand, this method takes advantage of the same autocorrelation matrix,which can be rank de ficient in the presence of coherences. Then, the location of each peak has corresponded with the DOAs to the broadband radio signals, and DOAs value for the broadband signal can be obtained,

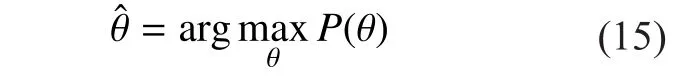
Based on the wavelet algorithm, the wavelet MVDR algorithm can improve greatly the ability of solving the correlation problem by using the frequency domain smoothing.According to the principle of multiresolution wavelet transformation, the array received signal is the superposition of multiresolution.After doing the wavelet transformation for the received signal, the different resolution of the signal can be observed by the multiresolution decomposition. Therefore, the signal can be defined by the multiscale of the wavelet, and the wavelet multiresolution analysis can improve the signal DOAs estimation resolution.

V. CONVERGENCE ANALYSIS

VI. SIMULATION EXPERIMENTS

The support length of Daubechies and Symmlets wavelets are shorter than the Coiflets wavelet, which have better concentrated of the wavelet decomposition energy, and less of the spectrum leakage, which reduced the DOAs estimation error. So several examples are presented using Symmlets wavelets to illustrate the performance of the proposed algorithms in following experiment. In the first experiment,there is a uniform linear array antenna system with 20 array elements, and the spacing be-tween the array elements is half wavelength of the maximum center frequency of the signals;the maximum frequency is 200kHz, and the lowest frequency is 20kHz; the reference frequency point is the frequency center, and the snapshot number on each frequency is 50. The corresponding DOAs are -400,-200,100,400,600, the AWGN noise is SNR=5dB. Assume these received signals have same power, the-400is the main signal, and others are the interference. The detail of behavior of standard MVDR, FFT MVDR and proposed algorithm approaches around the DOAs of interest is showed in Figure 2. In Fig. 2, because the proposed algorithm can filter out the large power interference signal, the power at the user -400is more than others users.

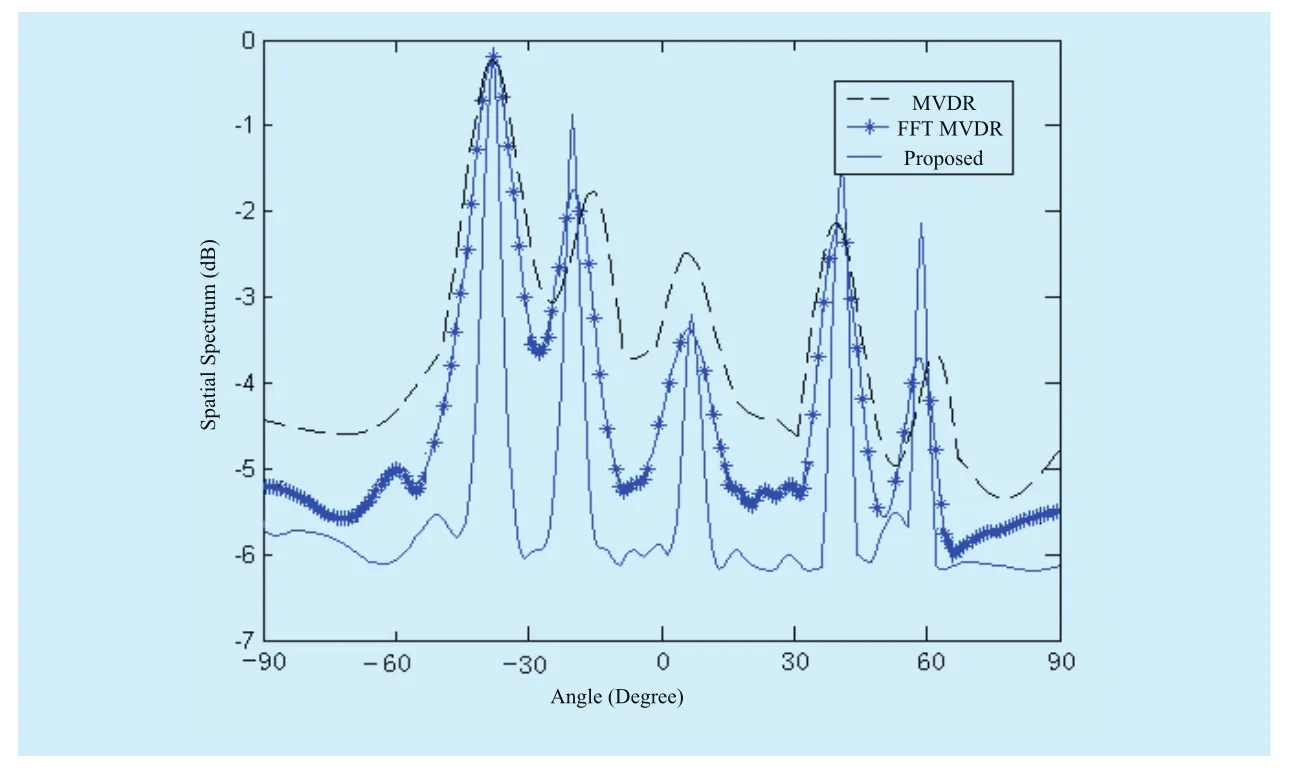
Fig. 2 Comparison DOAs estimation of MVDR, FFT MVDR and proposed algorithms

Fig. 3 Comparison DOAs estimation with three correlated signals in Gaussian noise

In the second experiment, the array situation and broadband signal bandwidth and power are same as the first experiment. The main characteristic of multipath signals is correlation. This simulates a multipath situation where the incident angles for broadband signal are correlation among -100,-140,-180. The signals corrupted by the Gaussian noise that SNR=5dB. We use the wavelet transformation with three decomposition lays. The interest DOAs of proposed algorithm, FFT MVDR,and traditional MVDR detail behaviors are showed in Figure 3. The proposed algorithm and FFT MVDR are able to detect both correlated signals, while the proposed algorithm achieves the best performance with a gain of several decibels between the peaks.

The computational costs in terms of the number of multiplications needed for computing thematrix with 20 array elements are listed in table 1, which gives a comparison between the proposed algorithm and the MVDR method. In table 1, the MVDR is much simpler than the proposed algorithm.With the proposed algorithm, a small number of J weights can be selected for updating,leading to a reduced number of multiplications in the computation. It is worth noting that the total number of multiplications may indicate a computational load, but not necessarily the hardware complexity. A small number of multiplications per iteration would be favorable for a low hardware complexity in practical implementation.

The simulations are accomplished on the personal computer whose CPU configuration and RAM are offered by AMD APU E-350 1.6 GHz and 2 GB DDR3, respectively. It can be concluded from Table 2 that the eigenvalue decomposition time of proposed algorithm is less than the MVDR. However, the simulation time of MVDR is less than that of proposed algorithm, because more number of iteration in proposed algorithm showed in Table 1.

In Figure 4 the convergence property of the proposed algorithm is studied. All three lines are under the same condition and different val-ues of SNR. Thedecreases as the number of iterations increases, and it converges faster as the SNR becomes higher, which are conceptually satisfying.

The performance of direction arrival algorithm is always evaluated by the root mean square error (RMSE) value. Finally, the simulation conditions are the same with the above simulation experiment, but the experiment frequency is improved from 0.5GHz to 2GHz.Figure 5 showed the DOAs behavior of FFT MVDR and proposed algorithm.

In Figure 5 the RMSE value in proposed algorithm is much smaller than the FFT MVDR algorithms. When the frequency is increased,the computer simulation time is increased significantly. The increased frequency range is conducive to the direction of arrivals estimation for source signals which in different frequency bands. However, the angular spacing between the sources would appear much closer, which, in turn, will make separation a much more difficult task for the different angle signal sources at the same frequency. But the proposed algorithm has the best resolution compared with the FFT MVDR algorithm, because the wavelet algorithm has a better signal resolution in high frequency. And at the higher frequencies, the main lobe direction points are better, and the side lobe patterns are lower than before, because of the array aperture principle.

VII. CONCLUSION

In this paper, we have proposed the DOAs algorithm to cope with the correlated signals in wireless radio communication. The proposed algorithm estimates each frequency DOAs,and the weighted average is obtained finally.The proposed algorithm can effectively reduce the estimation error at the low SNR situation and can quickly estimate the direction of arrival for the correlated signals comparing the classical MVDR algorithm. The new covariance matrix made by the proposed algorithm can improve the matrix rank value distribution to full rank, where the signal direction can be effectively estimated because of the fullyorthogonal between the signal subspace and the noise subspace. And use of the proposed framework improves the robustness against Gaussian and non-Gaussian noise sources.We can apply the new proposal in linear array with three or four elements. But the number of sources should not exceed the number of sensors too much. When the number of elements reduced, the sources closely spaced are increased. Under this extremely situation, it is more and more difficult for RMSE value to be satisfied, and the effectively DOAs is influenced by the SINR too. The main drawback of the presented algorithm is needed the large number of coefficients which increases the computational burden. Nevertheless, the covariance matrix that is done the optimization problem is always small, and thus, the increase of computation burden is can be accepted.

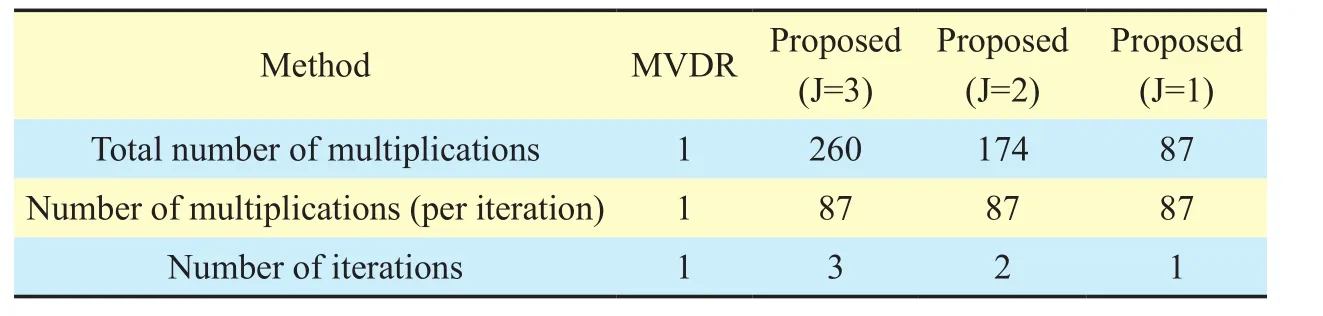
Table I Computational cost

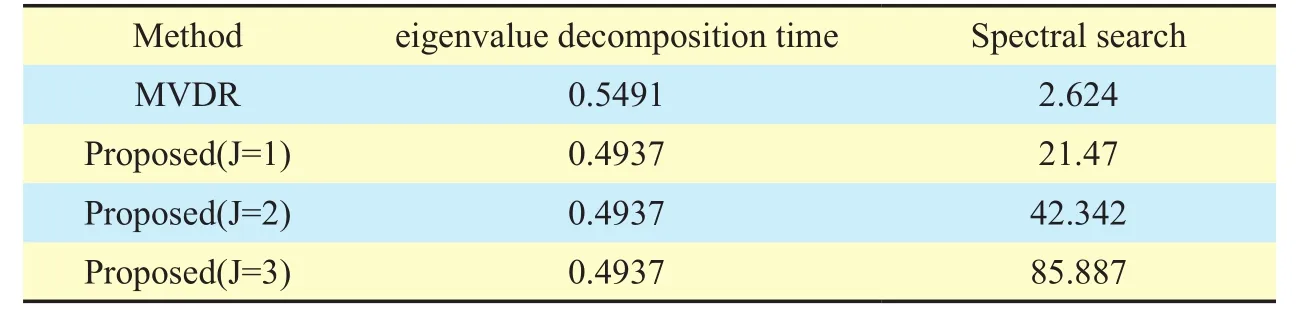
Table II Comparison of simulation time (s)

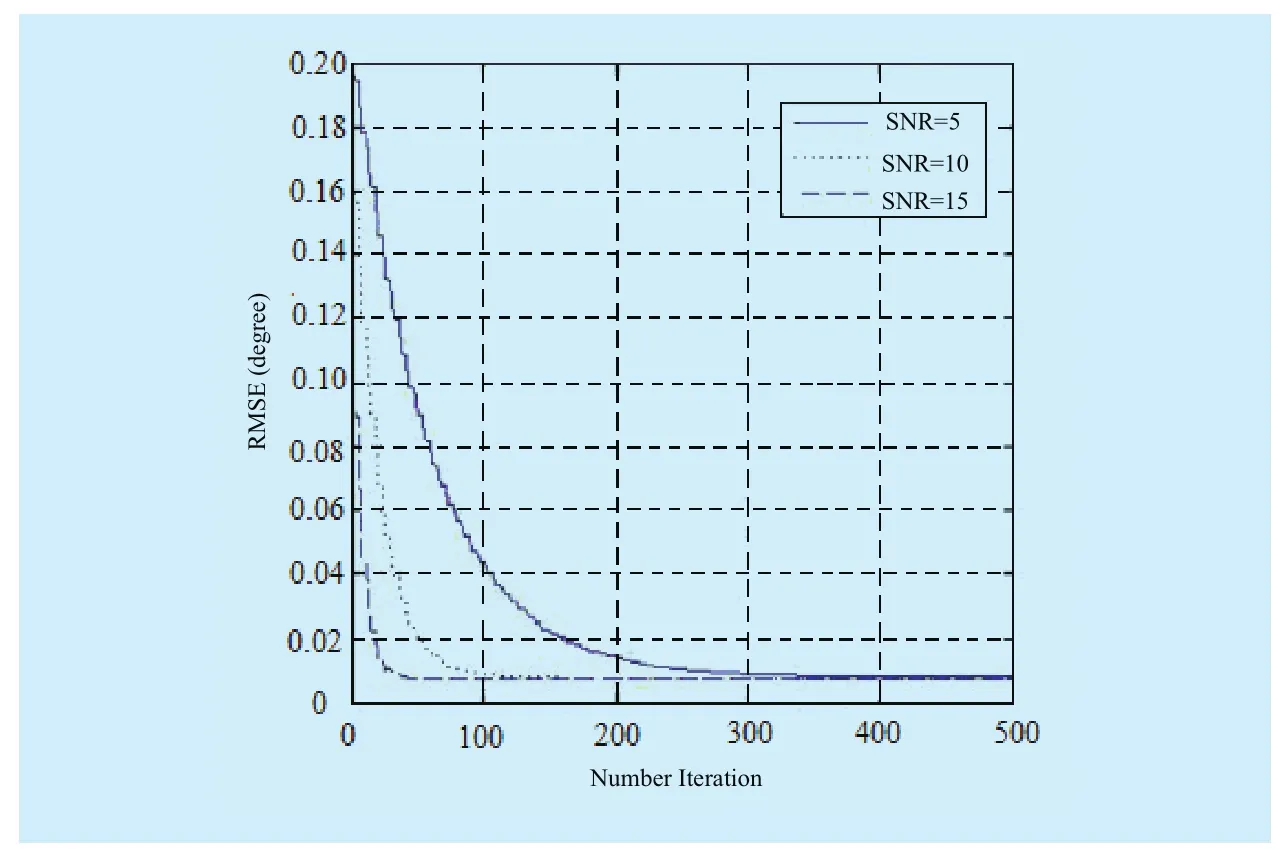
Fig. 4 Convergence property of the proposed algorithm

Fig. 5 Curves of RMSE Comparison in GHz

This work was supported by the Chinese Natural Science Foundation 61401075 and Central University Business Fee ZYGX2015J106.

Reference

[1] Bin Cao, Jia Yu, Ye Wang, Qinyu Zhang, “Enabling polarisation filtering in wireless communications: models, algorithms and characteristics”,IET Communications, vol.7,no.3,pp 247-254,May,2013.

[2] Pau Bofill, Michael Zibulevsky, “Underdetermined blind source separation using sparse representation”,Signal Processing, vol.81, no.11,pp 2353-2362, November, 2001.

[3] O. Yilmaz, S. Rickard, “Blind separation of speech mixtures via time-frequency masking”,IEEE Trans. On Signal Processing, vol.52, no. 7,pp 1830-1847, June, 2004.

[4] F. Abrard, Y. Decille, “A time-frequency blind signal separation method applicable to underdetermined mixtures of dependent sources”,Signal Processing, vol.85, no.7, pp 1389-1403,July, 2005.

[5] R. Schmidt, “Multiple emitter location and signal parameter estimation”,IEEE Trans. on Antenna Propagation, vol.34, no. 2, pp 276-280,January, 1986.

[6] R. Roy, T. Kailath, “Esprit-estimation of signal parameters via rotational invariance techniques”,IEEE Trans. on Acoustic Speech Signal Processing,vol.37, no.7, pp 984-995, August, 1989.

[7] P. Vallet,X. Mestre, P. Loubaton, “Performance analysis of an improved MUSIC DoA estimator”,IEEE Trans. on Signal Processing, vol.63, no. 23,pp 6407-6420, August, 2015.

[8] Pengfei Li, Min Zhang, “ Research on direction of arrival estimation based SVM”,Systems Engineering and Electronics, vol.31, no. 11, pp 2571-2574, November, 2009.

[9] Y. S. Yoon, L M Kaplan, J. H. McClellan, “TOPS:new DOA estimator for wideband signals”,IEEE Trans. on Signal Processing, part1 , vol.54, no. 6,pp 1977-1989, June, 2006.

[10] Bin Liao, S.C. Chan, “A cumulant-based approach for direction finding in the presence of mutual coupling”,Signal Processing, vol.104, no.6, pp 197-202, November, 2014.

[11] J. Dai, Z. Ye, “Spatial smoothing for direction of arrival estimation of coherent signals in the presence of unknown mutual coupling”,IET Signal Processing, vol.5, no. 4, pp 418-425, July,2011.

[12] Zhoug fuye, Xu Xu, “DOA estimation by exploiting the symmetric configuration of uniform linear array”,IEEE Trans. on Antennas and propagation, vol.55, no. 12, pp 3716-3720, December,2007.

[13] Li Jian, P. Stoica, “Efficient mixed-spectrum estimation with applications to target feature extraction”,IEEE Trans. on Signal Processing,vol.44, no. 2, pp 281-295, August, 1996.