Efficient XML Query and Update Processing Using A Novel Prime-Based Middle Fraction Labeling Scheme

Zunyue Qin , Yong Tang, Feiyi Tang, Jing Xiao, Changqin Huang, Hongzhi Xu

1 Department of Computer Science, SunYat-sen University, Guangzhou 510006, China

2 School of Computer Science, South China Normal University, Guangzhou 510631, China

3 College of Engineering and Science, Victoria University, VIC, 3011, Australia

4 School of software, Jishou University, Zhangjiajie 427000, China

I. INTRODUCTION

XML is a de facto standard for data exchange on the Internet, XML data management presents several new features in the cloud computing environment[1,2,3,4,5,6,7], and the XML data have been widely used in configuration languages[8,9]. In addition,uncertainty management of XML data has become a research focus, with high-performance computing of LCA[10,11,12,13] at the core. Whether in XML data processing in the cloud computing environment or in management of uncertain XML data, efficient query is always the basis to process XML data.Structural index of XML can be set up to further improve query efficiency, the structural index of sequential XML documents includes node index[14,15,16,17,18,19], sequential index[20,21], and graph index[22,23,24,25].Node index is used to complete twig query[26]; if the sequential index is used in twig query, but false positives and omission may occur[27].

Node index is achieved by encoding the nodes of XML documents. Common labeling schemes include region and prefix. Region labeling[18] uses the inclusion relation among node encodings to determine the structural and sequential relations between any two nodes, while prefix labeling[16] uses the prefix-matching relation between node encodings to determine the structural and sequential relations between any two nodes. The two labeling schemes have their own advantages and disadvantages. For example, region labeling adopts numbers to denote node encoding,so its length is fixed; prefix labeling adopts strings to denote node encoding, so its length enlarges as the depth and fan-out of the XML document increase. However, when new nodes are inserted, the two labeling schemes both require the second encoding of other nodes,which leads to lower updating efficiency.

In this article, a labeling method is proposed to separate the structural information from the sequential information of the XML document.

Therefore, a new labeling scheme called Prime-Based Middle Fraction labeling scheme(PMFLS) is designed in this study. PMFLS has the following advantages: first, the labeling length of PMFLS is fixed and irrelevant to the depth and fan-out of sequential XML document; second, numbers are used to present the encoding of nodes, obtaining the path information of the node is also easy using the proposed scheme, and thus, queries can be processed more efficiently; third, when new nodes are inserted in the sequential XML document, relabeling or recalculation of other nodes is entirely avoided and no complicated computing is required to guarantee high effi-ciency of updates.

The main contributions of the study are as follows: (1) the problems of different labeling schemes in supporting query and update are analyzed, and the labeling method that separates structural information in the hierarchical structure model from sequential information is proposed; (2) PMFLS is proposed according to the new labeling method, and algorithms are designed to realize PMFLS; (3) PMFLS can effectively handle the structure relation query of the sequential XML document and the update computing, and can occupy a reliable and very small space.

The rest of this paper is organized as follows: in Section 2, the characteristics, advantages, and disadvantages of labeling schemes such as region, prefix and binary labeling are introduced; in Section 3, the labeling method that separates structural information in hierarchical structure from sequential information between nodes is proposed, PMFLS is then proposed and implemented; we present our experimental study on labeling size, query performance, and update performance in Section 4; and conclude the paper in Section 5.

II. RELATED WORK

The node index determines the specific position of a node in the XML document tree by giving a encoding to each node, which is the most widely applied in the XML structural index. The most common node index includes region and prefix labeling.

2.1 Prefix labeling scheme

The Dewey labeling [16] is a typical prefix scheme, this scheme uses a digital vector to denote the path from the root to a specific node in the XML tree, determining the relation between nodes is easy through prefix matching. Figure 1 shows the XML tree using the Dewey scheme.

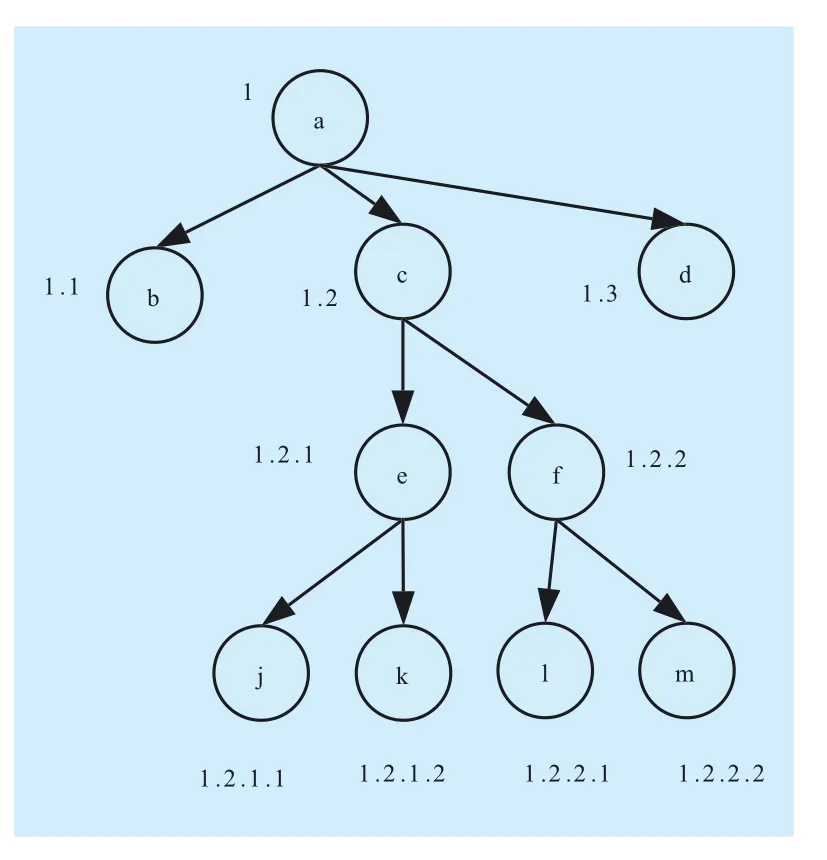
Fig. 1 Dewey scheme

The prime-based labeling[17] is also a prefix scheme. In prime-based labeling, the encoding of each node is represented by the product of the parent’s value and a prime number, and the structural relation between nodes can be determined by the divisibility. Figure 2 shows the XML tree using a prime-based scheme.

O’Neil et al. [15] proposed a labeling scheme similar to that by Dewey, namely, the ORDPATH scheme. In this scheme, an odd number is adopted to denote the encoding of nodes during initialization and an even number is used when new nodes are inserted.

2.2 Region labeling scheme

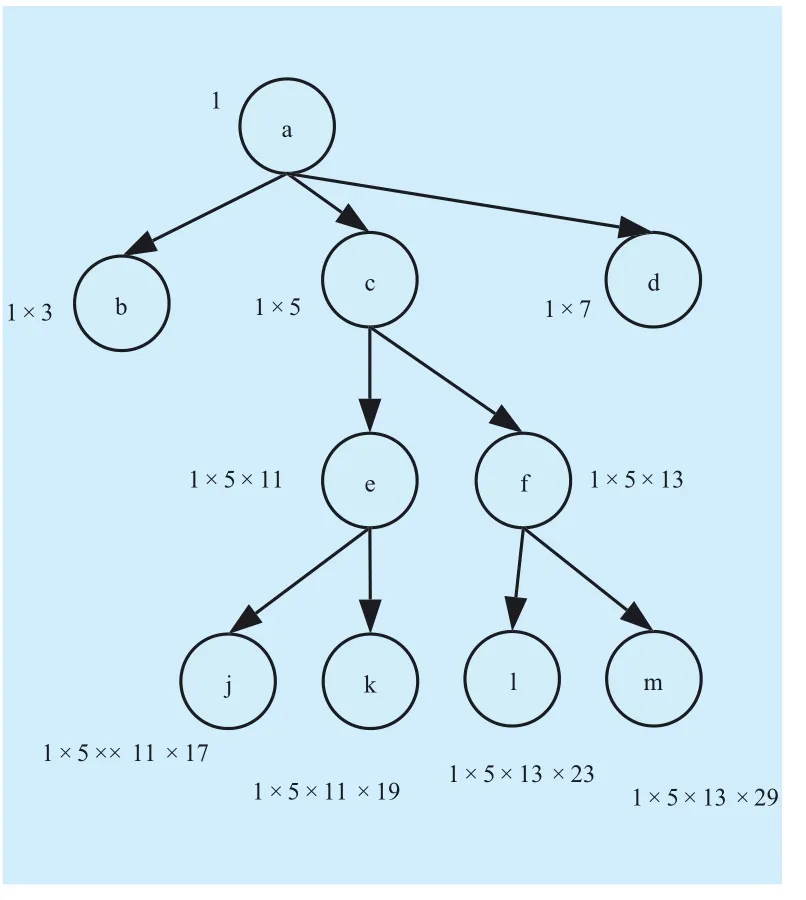
Fig. 2 Prime-based scheme

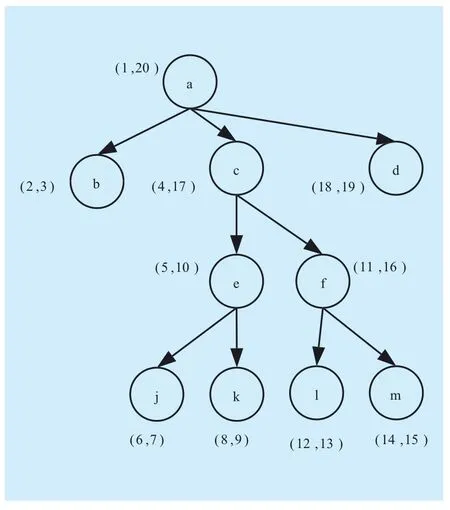
Fig. 3 Region scheme

Zhang et al.[18] have proposed the region labeling scheme, in which two-tuples (Begin,End) are allocated to each node of the XML tree, “Begin” is the serial number when the node is accessed for the first time and “End”is the serial number when the node is accessed for the second time. If the region of node v contains the region of the other node u, then v is the ancestor of u. By comparing the values, the labeling scheme is able to determine the structural and sequential relations among nodes rapidly. However, modifying the encoding of other nodes is required when new nodes are inserted, which leads to low updating efficiency. Figure 3 shows the region labeling.Li & Moon[14] have proposed another region scheme, in which two-tuples (order, size)are allocated to each node of the XML tree.“Order” is the serial number of the preorder traversal of the XML tree, and “size” is the number of descendant nodes. By using the redundancy of “size,” the labeling scheme can provide a partial solution to the problem that new nodes are inserted instead of the second encoding of other nodes.

2.3 Motivation

To support the updates of insertion effectively, the proposed labeling scheme extends region and pre fix labeling to a certain extent,but problems still exist. QED[28] is a prefix scheme, each node adopts the quaternary encoding method. Although QED solves the problem of inserting updates, its query efficiency is also positively correlated to depth similar to that of Dewey scheme. ORDPATH[15] and DDE[29] are also extensions of prefix scheme and solve the updating-related problem, however, similar to that of QED, its query efficiency is very low. LLS [30] integrates the advantages of region and prefix labeling, the scheme is able to determine the relation between nodes within constant time, and the encoding length is fixed, however, the encoding of some nodes still needs to be modified when updates are inserted, thus, its updating efficiency will be improved further. Ko & Lee[31]improved CDBS[32] and proposed IBSL.Among all kinds of labeling schemes based on binary string, they can completely avoid the second encoding of other nodes when new nodes are inserted. Nevertheless, the labeling space increases very rapidly, therefore, in turn,the rapid growth of labeling space also has a negative effect on query performance.

The quality of a labeling scheme is determined by the following three factors: 1)whether the labeling supports query effectively; 2) the stability of labeling space when the depth and fan-out of XML document undergo dynamic changes; and 3) whether the scheme supports the update computing of XML document effectively without the relabeling other nodes.

Given that region labeling uses number to represent the encoding of node and the length is fixed, only the complexity of constant time is required when the relation between nodes is computed, this feature is the basis of efficient node index and can be extended to prefix scheme. Therefore, we propose PMFLS in which number is used to encode nodes and the labeling length is irrelevant to the depth and fan-out of the XML tree, and the novel scheme is able to determine the ancestor–descendant relation and the parent–child relation between nodes within constant time. Finally, PMFLS completely meets the requirement that new nodes are inserted without the relabeling other nodes.

2.4 Cause analysis

Dewey is a typical prefix scheme, the scheme is able to compute the ancestor–descendant and parent–child relation between nodes as well as the sequential relation between nodes.Region scheme is able to compute the ancestor–descendant and the sequential relation between nodes, to compute the parent–child relation between nodes, hierarchical information is added and the encoding of each node is a triple (Begin, End, Level). Relabeling other nodes is required after a new node is inserted during Dewey and region scheme, because the encoding of nodes contains the structural and sequential information. Figure 4 shows that new node x is inserted between b and c,relabeling c ,d and their descendant need to relabel, because each encoding expresses the structural and sequential information of nodes in Dewey and region scheme. For example,the encoding of c is 1.2, where “2” is the ancestor information of low-level nodes such as e and f, and also the sequential information of the second level (the following-sibling of d and the preceding-sibling of b), therefore,when x is inserted, the encoding of x is 1.2 and the encoding of c is changed to 1.3, since“2” that node c uses to express structural information is changed to “3”, the encoding of its descendant nodes must be changed (i.e.,the encoding of nodes such as e and f shall be changed); moreover, the sequential information is changed from “2” to “3”, as a result, the sequential information of node d is changed to“4”, if d has some descendant nodes, then the encoding of these descendant nodes shall also be changed. The dashed line in figure 4(Corresponding to figure1) indicates the scope of updating after new nodes are inserted.

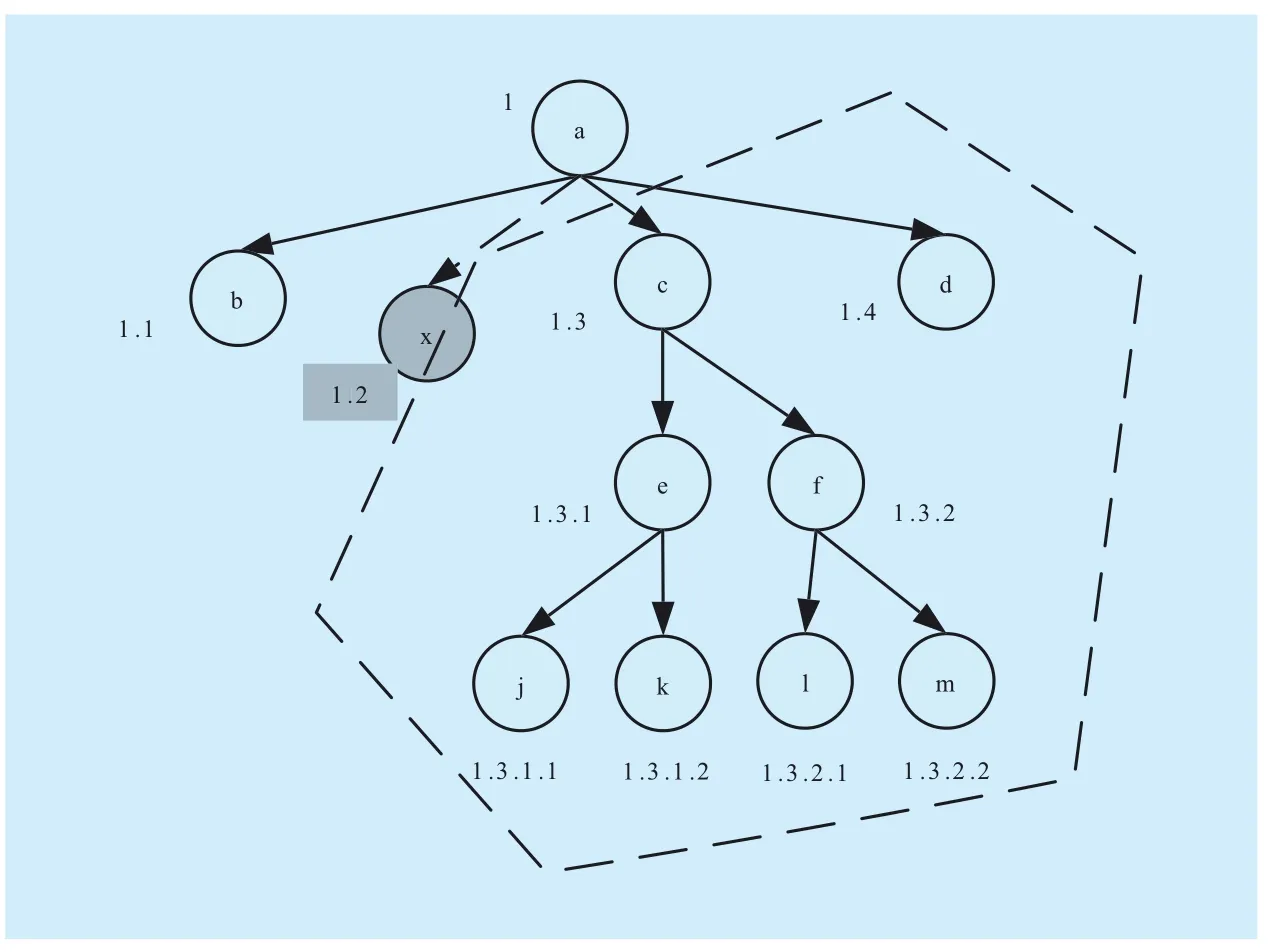
Fig. 4 Scope of updating for Dewey

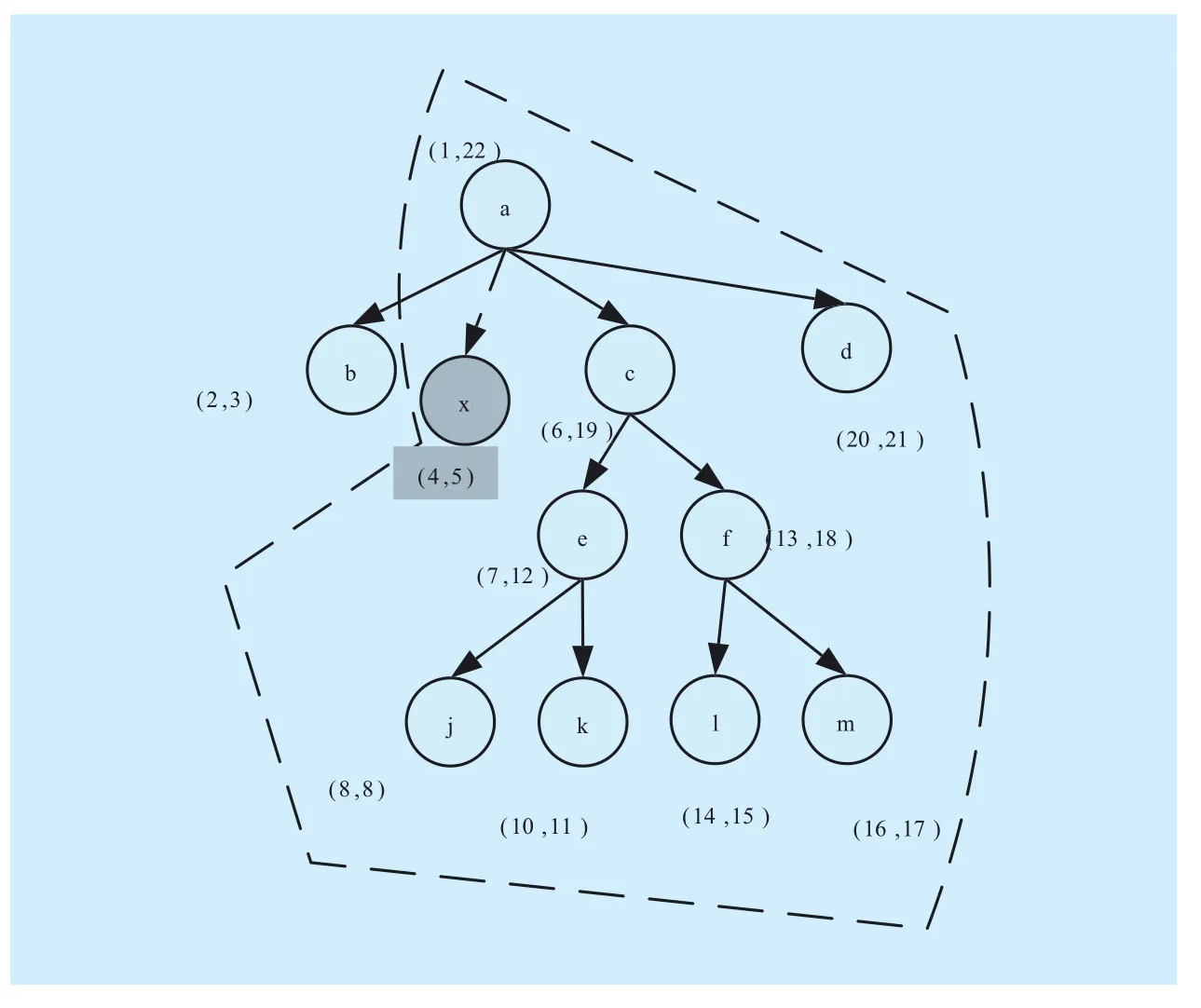
Fig. 5 Scope of updating for region

The same problems exist in region scheme,as shown in figure 5. Node x is inserted in figure 5, the serial number for the first access of x is 4. The serial numbers for the first access of nodes after x are all changed accordingly. “Begin” represents the serial number of preorder, but its value also contains structural information based on the judgment rule of structural relation (Begin(v)＜Begin(u), and End(v)＞End(u)), therefore, after x is inserted,the value of “Begin” in the encoding of other nodes is changed accordingly. Similarly, the value of “End” is also changed. The number of nodes requiring the relabeling in region scheme is more than that in Dewey. The dashed line in figure 5(Corresponding to figure 3) shows the scope of nodes whose encoding has to be changed.

The quality of a labeling scheme is determined by the following three factors: 1) whether the labeling supports query effectively; 2) the stability of labeling space when the depth and fan-out of XML document undergo dynamic changes; and 3) whether the scheme supports the update computing of XML document effectively without the need for relabeling.

In accordance with the aforementioned updates problems and the advantages of prefix and region scheme, a new method that expresses the structural information and sequential information of the XML document is separately proposed. In this way, when the structural information changes, the sequential information is uninfluenced and vice versa,moreover, the insertion updates are completely supported and the labeling length remains fixed.

III. PMFLS LABELING SCHEME

3.1 PMFLS

Based on the method that expresses the sequential information and structural information of sequential XML document separately,we propose the notion of “middle fraction” to meet the requirement that the sequential information remains orderly and the recalculation or relabeling of other nodes is unnecessary when a new node is inserted. To improve the updating efficiency, we also suggest the other notion “product of unique prime numbers” to meet the requirement that the path information of the node is saved to improve the query efficiency, and the structural information of other nodes are not adjusted when a new node is inserted.

De finition 1middle fraction. For the fractions x=a/b and y = c/d (a, b, c, d ＞0), the middle fraction of x and y is z = (a + c)/(b +d).

Property 1if the fractions x=a/b and y=c/d(a, b, c, d ＞0), x＜y, and the middle fraction is z, then x＜z＜y.

Proof: (1) Prove x＜z, i.e. a/b＜(a+c)/(b+d).Since a/b＜c/d and ad＜bc, it is inferred that ad+ab＜bc+ab, i.e. a(d+b)＜b(a+c), by changing the formula, we get a/b＜(a+c)/(d+b); (2)similarly, we can prove z＜y. Based on (1) and(2), we get x＜z＜y.

Example 1: if x=1/3 and y=1/2, then the middle fraction z=2/5, 1/3＜2/5＜1/2.

Definition 2product of unique prime numbers. The product of several different prime numbers is called the product of unique prime numbers.

Example 2: 2×3×11 is the product of unique prime numbers, while 3×3×11 is not.

Definition 3sequence of minimum middle fraction. The sequence of middle fraction generated by initial values 0/1 and 1/0 is called the sequence of minimum middle fraction.

Example 3: a part of the sequence of middle fraction generated on the basis of Definition 3 is 0/1, 1/3, 1/2, 2/3, 1/1, 3/2, 2/1, 3/1, 1/0,and the middle fraction grows very slowly.The test result shows that the maximum of denominator was 2,584 when 131,073 middle fractions were generated.

As mentioned, the sequential information and structural information of the XML document are expressed separately, the middle fraction is used to express the sequential information, by virtue of the uniqueness of the product of unique prime numbers and the uniqueness of factorization, the product of unique prime numbers is used to express the structural information.

Definition 4PMFLS. With respect to the sequential XML document tree T, based on the method that expresses structural information and sequential information separately,the PMFLS encoding of node v is a triple(parent StructInfo, self Prime, middleFraction), in which parentStructInfo represents the structural information of the parent node of a certain node, and parentStructInfo(v)=parent-StructInfo (parent(v))×selfPrime(parent(v));selfPrime is a prime number, if the node is not a leaf node, then the prime number is different from the prime number of other nodes, if the node is a leaf node, then the prime number is 2; middleFraction represents the sequential information, and a middleFraction is generated on the basis of Definition 3.

Example 4: Based on Definition 4, figure 6 shows the PMFLS of the sequential XML document tree. In the figure, we try to compute the encoding of node b. As defined, parentstructInfo(b)= parentStructInfo(parent (b))×-selfPrime(parent(b)), and thus, the structural information of node b is 1, given that node b is a leaf node, selfPrime(b)=2, middleFraction(b)=1/3, and PMFLS(b)=(1,2,1/3). For node f, parentStructInfo(f) =parentStructInfo(parent(f))×selfPrime(parent(f))=1×5=5,selfPrime(f)=13, and middleFraction(b) =3/2,hence, PMFLS(f)=(5,13,3/2). For node k, parentStructInfo(k)=1×5×11, given that k is a leaf node, selfPrime(k)=2, middleFraction(k)=4/3,and PMFLS(k)=(55,2,4/3).

Figure 6 also shows that nodes e and f have the same parentStructInfo, and thus, they are siblings. Given that middleFraction(e)＜middleFraction(f), e is the preceding sibling of f. For node k and e, parentStructInfo(k)=parentStructInfo(e)×selfPrime(e), thus, e is the parent of k. For nodes c and k, parentStructInfo(k) mod parentStructInfo(c)×selfPrime(c)=0,therefore, c is the ancestor of k.

3.2 Main algorithms

When the sequential XML document is queried, computing the ancestor–descendant and parent–child relation between nodes as well as the sequential relation among nodes is necessary. PMFLS supports the computation of these relations.

Algorithm 1 can compute the structural relation between any two nodes including the ancestor–descendant relation and parent–child relation. The basic principle of Algorithm 1 is as follows: for nodes u and v, parentStructInfo(u)＜parentStructInfo(v),if parentStructInfo(v) mod (parent StructInfo(u)×selfPrime(u))=0, then u is the ancestor of v; if parentStruct-Info(u) × selfPrime(u)= parentStructInfo(v),then u is the parent of v; if selfPrime(u) u is an even number, which means that the node is a leaf node.

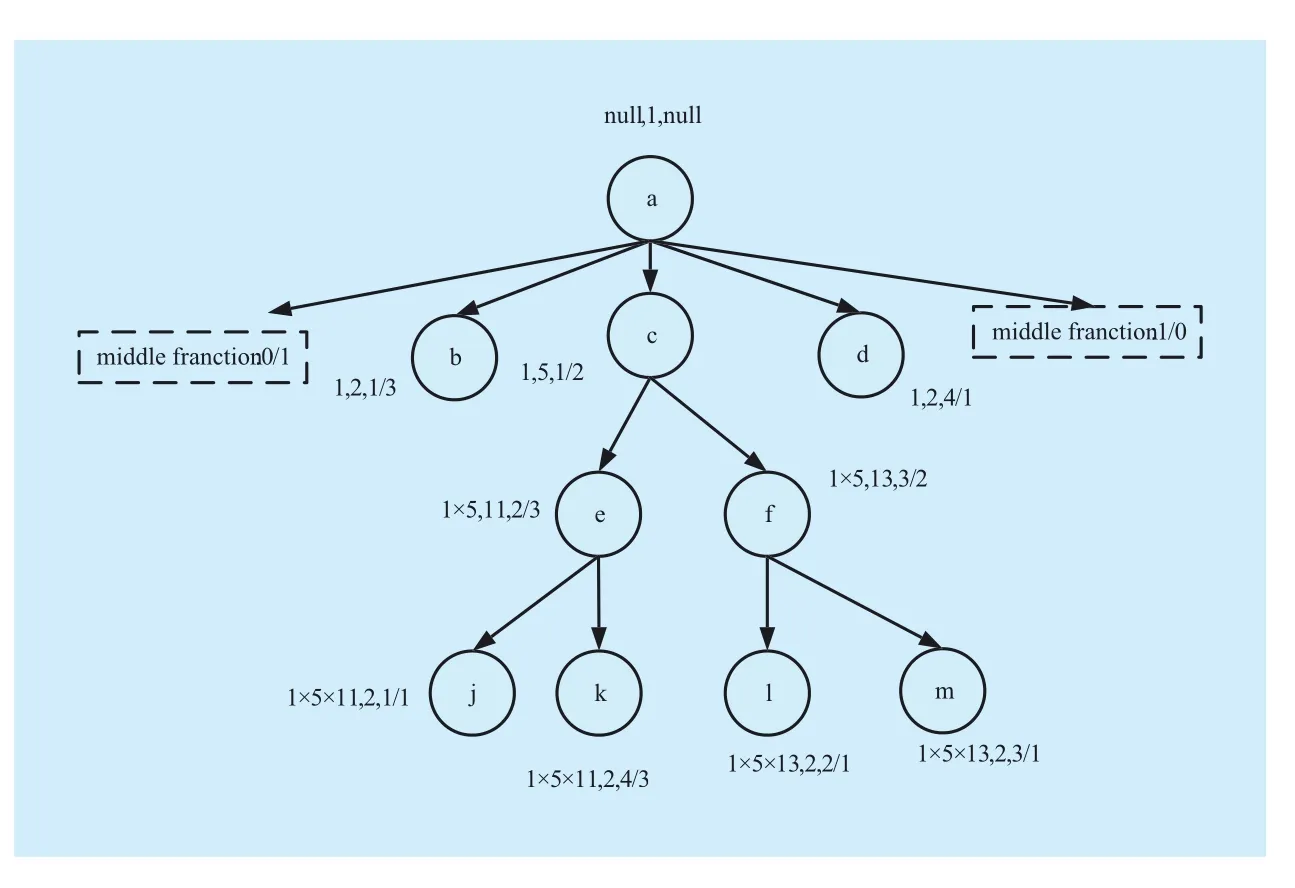
Fig. 6 PMFLS

Example 5: nodes c and k in figure 6, parentStructInfo(k)=55(1×5×11), parentStruct-Info(c)× selfPrime(c)=5(1×5), and 55 mod 5=0, c is the ancestor of k; for nodes e and k,parentStructInfo(e)=5, selfPrime(e)=11, and parentStructInfo(e)×selfPrime(e)=55, thus, e is the parent of k; for nodes d and k, parent-StructInfo(d)＜parentStructInfo(k) and self-Prime(d) is an even number, which indicates that d is a leaf node, thus, d is not the ancestor of k.

Algorithm 1 struct Relation(u,v)

Algorithm 2 sibling Relation(u,v)

Algorithm 3 insertNode(p,u,v);//insert a new node x between u and v, p is parent of x

Algorithm 2 is able to compute the sibling relation between any two nodes. The basic principle of Algorithm 2 is as follows: for nodes u and v, if u and v are siblings and middleFraction(u)＜ middleFraction(v), then u is the preceding sibling of v; otherwise, u is the following sibling of v.

Example 6: Nodes e and f in figure 6, given that parentStructInfo of e and f are both 5, and middleFranction are 2/3 and 3/2, 2/3/< 3/2, e is the preceding sibling of f; for nodes k and m, their parentStructInfo are different; thus, k and m are not siblings.

It is very easy to compute the sequential relation between any two nodes. The basic principle is as follows: for nodes u and v, if middleFraction(u)＜middleFranction(v), then u is the preceding of v, otherwise ,u is the following of v.

Example 7: in figure 6, regarding nodes e and m, middleFranction(e)＜middle-Franction(m), as a result e is the preceding of m.

PMFLS is used to label the sequential XML document tree, new nodes can be inserted at any location, furthermore, the relabeling and recalculation of other nodes are unnecessary and the sequential relation between nodes can be maintained. Algorithm 3 is able to insert new nodes at any location without the relabeling and recalculation of other nodes.

Example 8: figure 7 shows two different conditions in which new nodes are inserted.(1) According to algorithm 3, when inserting x1, c is parent x1, x1 is between k and f, thus middleFraction(x1) =7/5 (=middleFraction(k)+ middleFraction(f)), parentStructInfo(x1)=5(=parentStructInfo(c)×selfPrime(c)), self-Prime(x1)==2; (2) a new node x2 is inserted under the leaf node m, According to algorithm 3, selfPrime(m) = 17, parentStructInfo(x2)=1×5×13×17(=parentStructInfo(m)×self-Prime(m)), middleFraction(x2) =7/2 (=middleFraction(m) + middleFraction(d)), self-Prime(x2)=2.

IV. PERFORMANCE EVALUATION

To examine the performance of PMFLS, its labeling space, query performance and code update are tested. The proposed PMFLS is compared with the representative labeling schemes that support updating, such as DDE,IBSL, and QED-Dewey.

All experiments are conducted on a computer with Intel Pentium 2.8 GHz CPU, 4G memory, and Windows 7 operating system.JDK6.0 is used to implement the PMFLS of the XML document. The datasets and their properties are presented in Table 1.

4.1 Static performance

DDE, IBSL, QED-Dewey and PMFLS are applied to initialize the labeling of four datasets in Table 1, their static performance is tested.

4.1.1 Time for initialization

Figure 8(a) shows the comparison of time to initialize the encoding of four different labeling schemes. For datasets D1, D2, and D3, PMFLS presents the best performance in initialization time. The reason is that IBSL and QED-Dewey need to generate all sequences of encoding value before initializing nodes, and the generated encoding value is then used to encode all other nodes. By contrast, PMFLS uses prime numbers to directly encode without any additional computation, and its sequential information is express by middleFranction,to simplify the labeling operation. For dataset D4, PMFLS has a time performance that is close to that of DDE and superior to that of IBSL and QED-Dewey, the reason is that large numbers are required to store parentStructInfo in the case of many internal nodes, and thus,the labeling performance is reduced.

4.1.2 Labeling length

Figure 8(b) shows the labeling size when the fan-out and depth of the four encoding schemes reach their maximum. The results show that PMFLS’s size is more stable. On the contrary, the labeling length of the other three schemes increase with the growth of fanout and depth. The reason is that DDE and QED-Dewey use prefix to store the path information and the encoding of each node contains the information of ancestors, as a result,larger depth leads to more ancestors and longer labeling length. IBSL is a binary labeling scheme, although it improves the storage ratio effectively, its labeling length increases with the growth of depth because of the application of prefix.

4.1.3 Query performance

We queried four relations of sequential XML document, i.e., whether two nodes have an ancestor–descendant (referred to as AD hereafter) relation, whether two nodes have a parent–child (PC) relation, whether two nodes have a sibling (Sibling) relation, and the sequence in which nodes occur in document(Doc). Dataset D1 was used to test the four relations mentioned. The query statement is shown in Table 2, and the test result is shownin Figure 8(c). As shown in the figure, PMFLS presents the best time performance in the AD,PC, Sibling and Doc relations. PMFLS uses numerical value to express structural information, For PMFLS, computing the four relations mentioned is irrelevant to the depth of nodes and its labeling length is small. On the contrary, the other four schemes have larger labeling length and is proportional to the depth of nodes when computing the four relations,thus, the query performance of PMFLS has a significant advantage.

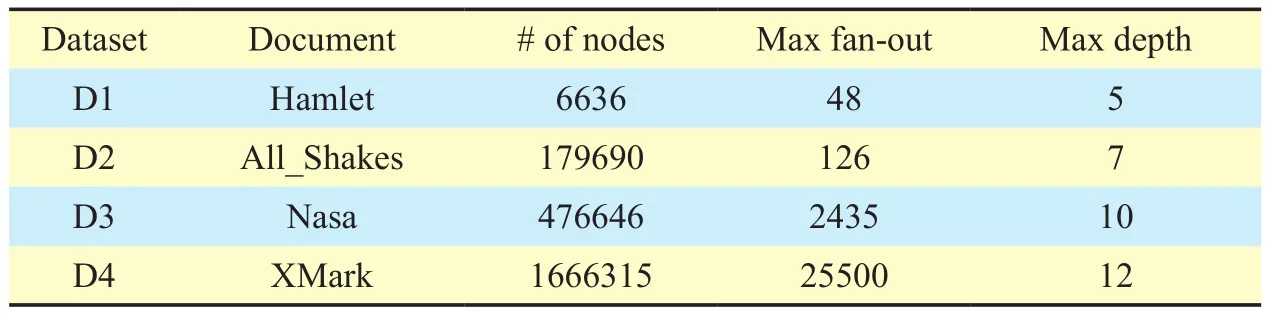
Table I Test datasets

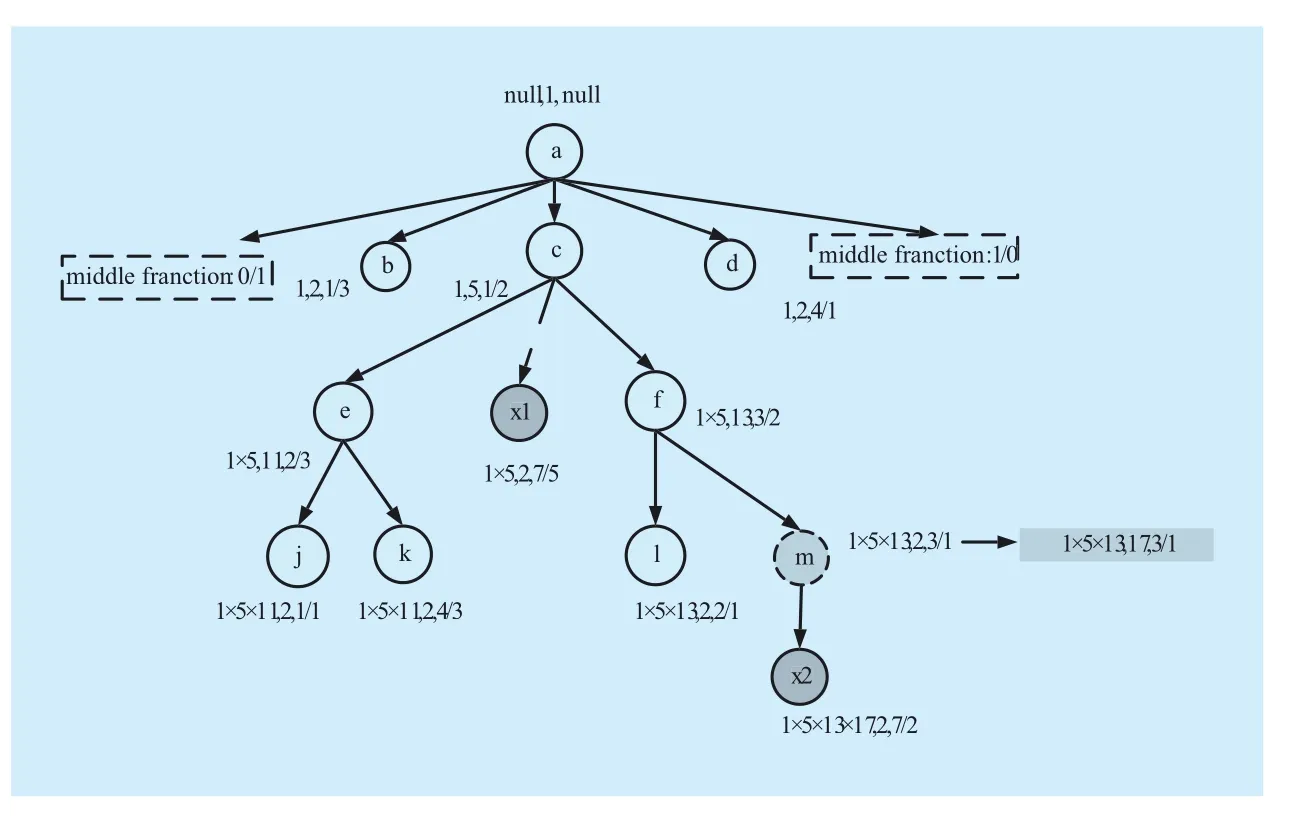
Fig. 7 New nodes inserted at different locations

Table II Test queries on Dataset D4

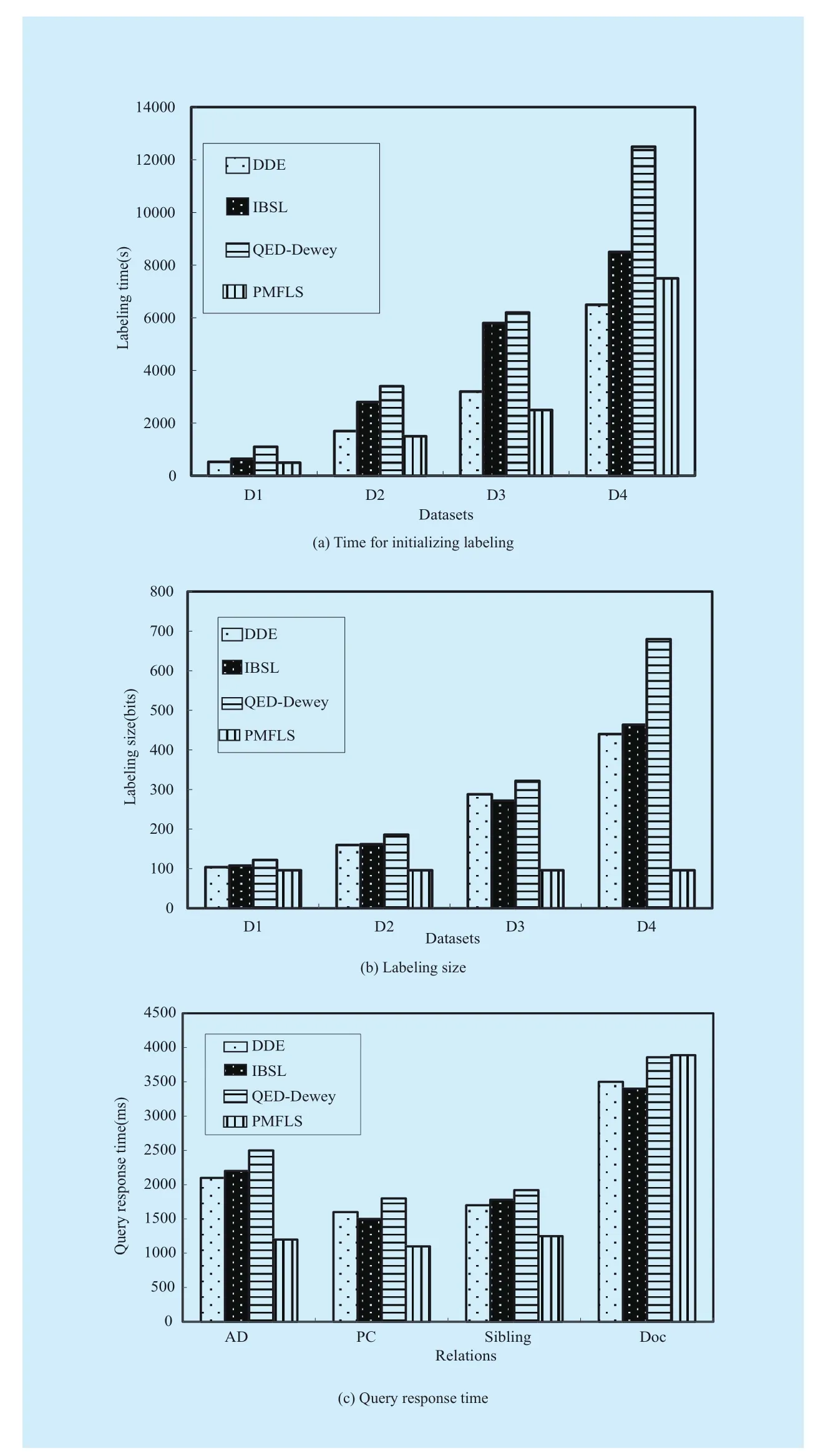
Fig. 8 Static performance study on labeling schemes

4.2 Dynamic performance

To examine the dynamic performance of the labeling schemes accurately, uniform insertion and skewed insertion were tested. Uniform insertion refers to the process in which 2n–1 nodes are inserted uniformly between two adjacent nodes. Skewed insertion refers to the process in which n nodes are inserted in some fixed location continuously.

4.2.1 Uniform insertion

To test the performance of inserting new nodes uniformly, we inserted 2n–1 nodes uniformly between play/act [1] /scene [1] /speech [1] and speech [2] of dataset D1.

Example 9: When n=1, a new node x1 is inserted between speech [1] and speech [2];when n=2, 2 new nodes x2 and x3 are inserted to form speech [1], x2, x1, x3, and speech [2];when n=3, 4 new nodes x4, x5, x6, and x7 are inserted to form speech [1], x2, x2, x5, x1, x6,x3, x7, speech [2], and so on.

● Labeling length

Figure 9(a) shows the updating when n=1,2, 3, …, 15. On the condition that the number of inserted nodes <128, the average length of inserted new nodes in DDE, IBSL, and QED-Dewey is smaller than that in PMFLS.However, as the number of inserted nodes increases, the average length of the inserted new nodes in PMFLS is smaller than that in the other three schemes. The reason is that the labeling length of PMFLS is a fixed value,whereas the labeling length of the other three schemes increases with the growth of fan-out. QED-Dewey uses quaternary numeral system that reduces the storage ratio, and thus, QED-Dewey has the maximum labeling length.

● Updating time

When new nodes are inserted, existing encodings are scanned to determine where nodes are inserted in all of the four schemes,as a result, the time complexity is the same,figure9(b) shows the updating time of the four schemes. As shown in the figure 9(b), PMFLS presents the best performance in inserting updates, query operation is required to determine where a new node is inserted, PMFLS has the best query performance and the relabeling of other nodes is unnecessary. The updating performance of IBSL is better than that of DDE and QED-Dewey, the reason is that its labeling length when nodes are inserted uniformly is smaller than that of the other two schemes,which leads to better time in query positioning.

● Query performance

After 4096 nodes are inserted uniformly between play/act [1] /scene [1] /speech [1] and speech [2] (n=12), the AD, PC, Sibling, and Doc relations among all inserted nodes were computed, figure 9(c) shows the time required by four encoding schemes. Regarding the query of AD, PC, Sibling and Doc relations,PMFLS is significantly advantageous. The reason is that the constant time for computing the relations is irrelevant to depth, fan-out,and labeling length, whereas that of the other three schemes is related to depth and labeling length.

4.2.2 Skewed insertion

In the case of skewed insertion, n(=100, 500,1000, 2000, 4000) nodes are inserted continuously after the fixed location play/act [1] /scene [1] /speech [1].

● labeling length

Figure 10(a) shows the average labeling length after n nodes are inserted. As the number of inserted nodes increases, the length of QED-Dewey grows rapidly, the reason is that its labeling length increases by O(n); the length of IBSL increases by half of that of QED-Dewey; and DDE’s labeling length increases more slowly.

● Updating time

Figure 10(b) shows the comparison of updating time when n nodes are inserted continuously. In the case of dynamic updating,given that the labeling length of QED-Dewey and IBSL grows rapidly and the time for computing new codes is related to labeling length,the two schemes have very low updating efficiency. DDE changes the property of prefix labeling and the original left and right vector labeling are decomposed to compute new encodings, as a result, the updating efficiency of DDE is also very low. PMFLS is able to compute new encodings directly using left and right, but such computing is irrelevant to the depth and labeling length of left and right, as a result, the updating efficiency of PMFLS is higher.

● Query performance

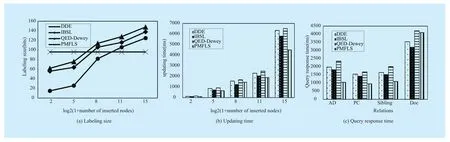
Fig. 9 Performance study on uniform insertions

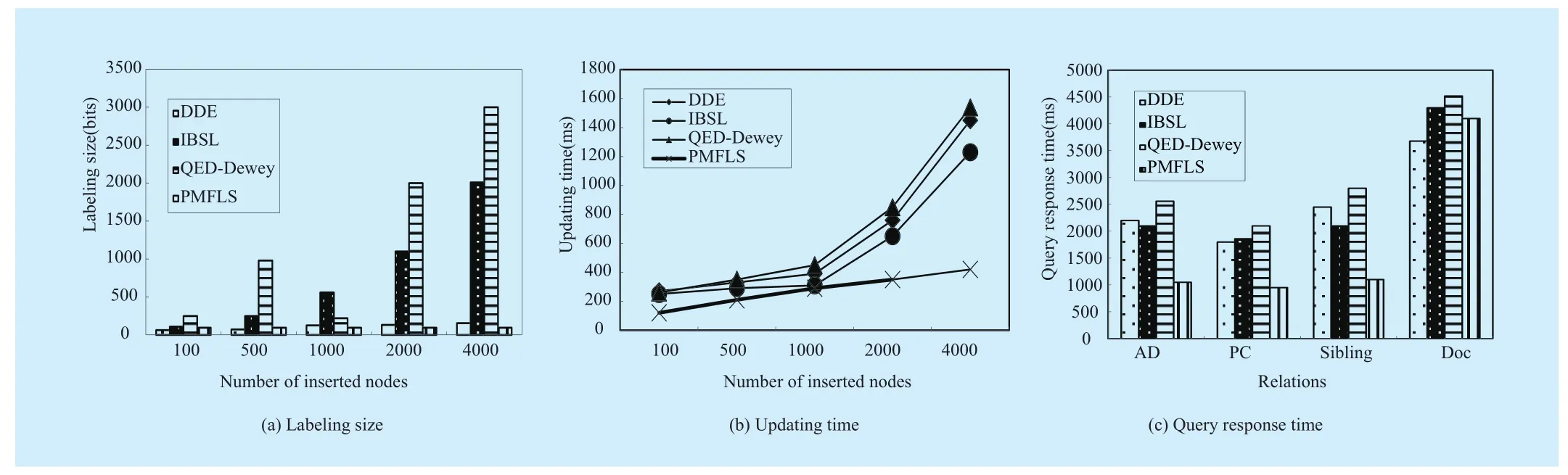
Fig. 10 Performance study on skewed insertions

A total of 4000 new nodes are inserted continuously after play/act [1] /scene [1] /speech[1], and the four query relations are tested.Figure 10 (c) shows the comparison of the time used by all labeling schemes. The figure shows that PMFLS performs extremely well when computing the AD, PC, Sibling and Doc relations, because its labeling length is fixed and irrelevant to depth during computation.But the labeling length of QED-Dewey and IBLS is very large and is related to depth and labeling length. DDE performs better than QED-Dewey and IBLS because of a smaller labeling length.

V. CONCLUSIONS

The advantages and disadvantages of prefix and region schemes were analyzed, the labeling method that separates the structural information from the sequential information of the XML document was proposed. Then a new labeling scheme of the XML document tree called PMFLS was designed. This scheme expresses the structural information and sequential information of the XML document separately. The structural relation and sequential relation are stored using integers, and the structural information among nodes can be determined rapidly within the time O(1) according to Algorithms 1 and 2, thus, the query performance is improved. Besides, middle fraction was used to represent the sequential relation. The proposed PMFLS is able to insert new nodes at any location and does not require the relabeling and recalculation of other nodes, accordingly, the updating efficiency of PMFLS is significantly improved. The proposed labeling scheme has a fixed length of storage, which ensures that the labeling length does not increase when new nodes are inserted frequently.

Further research may focus on how to design more effective structural encoding and sequential encoding with using the method that expresses structural information and sequential information separately, or on how to apply single encoding to include structural information and sequential information simultaneously as well as to complete the computation related to insertion of updates.

This work is supported by the National Science Foundation of China (Grant No.61272067, 61370229), the National Key Technology R&D Program of China (Grant No. 2012BAH27F05, 2013BAH72B01), the National High Technology R&D Program of China (Grant No. 2013AA01A212), and the S&T Projects of Guangdong Province (Grant No. 2016B010109008, 2014B010117007,2015A030401087, 2015B010109003,2015B010110002).

[1] Guo, L., Wang, J., & Du, H. “XML privacy protec-tion model based on cloud storage”.Computer Standards & Interfaces, Vol.36, No.3, pp. 454-464, March, 2014.

[2] Baqasah, A., Pardede, E., & Rahayu, W. “Maintaining schema versions compatibility in cloud applications collaborative framework”.World Wide Web-internet & Web Information Systems,Vol.18, No.6, pp. 1541-1577. November, 2015.

[3] Bi, X., Wang, G., Zhao, X., Zhang, Z., & Chen, S.“Distributed XML Twig Query Processing Using MapReduce”.Asia-Pacificweb Conference,Vol.9313, pp.203-214, November, 2015.

[4] Poon, H. T., & Miri, A. “Computation and Search over Encrypted XML Documents”.IEEE International Congress on Big Data, pp. 631-634, June,2015.

[5] Hsu, W. C., Liao, I. E., & Shih, H. C. “A cloud computing implementation of XML indexing method using Hadoop”.Asian Conference on Intelligent Information and Database Systems,Vol.7198, pp.256-265, March , 2012.

[6] Hsu, W. C., Shih, H. C., & Liao, I. E. “A scalable XML indexing method using MapReduce. Innovative Computing Technology”.Fourth International Conference on Innovative Computing Technology, pp.81-86, August, 2014.

[7] Diao E. “Task Partition Technology of pXCube Cloud Model”.China Communications, Vol.8,No.6, pp.93-99, October, 2011.

[8] Meller N; Liu YC; Collins TL; Bonnefoy-Bérard N;Baier G; Isakov N; Altman A. “XML to annotations mapping definition with patterns”.Computer Science & Information Systems, Vol.11,No.4, pp.1455-1477, October, 2014.

[9] Bou S, Amagasa T, Kitagawa H. “Path-based keyword search over XML streams”.International Journal of Web Information Systems, Vol.11,No.3, pp. 347-369, April, 2015.

[10] Bao Z, Zeng Y, Ling T W, et al. “A general framework to resolve the MisMatch problem in XML keyword search”.VLDB Journal, Vol.24, No.4,pp.1-26, August, 2015.

[11] Liu, X., Chen, L., Wan, C., Liu, D., & Xiong, N. “Exploiting structures in keyword queries for effective xml search”.Information Sciences, Vol.240,No.11, pp.56-71, August, 2013.

[12] Zhou, R., Liu, C., Li, J., & Yu, J. X. “ELCA evaluation for keyword search on probabilistic xml data”.World Wide Web-internet & Web Information Systems, Vol.16, No.2, pp. 171-193,March, 2013.

[13] Li, J., Liu, C., Zhou, R., & Yu, J. X. “Quasi-SLCA based keyword query processing over probabilistic xml data”.IEEE Transactions on Knowledge& Data Engineering, Vol.26, No.4, pp.957-969.April, 2014.

[14] Li, Q., & Moon, B. “Indexing and Querying XML Data for Regular Path Expressions”.In Proceedings of the 27th VLDB Conference, pp.361—370,September, 2001.

[15] O’Neil, P., O’Neil, E., Pal, S., Cseri, I., Schaller, G.,& Westbury, N. “Ordpaths: insert-friendly xml node labels”.SIGMOD 2004, pp.903-908, June,2004.

[16] Tatarinov, I., Viglas, S. D., Beyer, K., Shanmugasundaram, J., Shekita, E., & Zhang, C. “Storing and querying ordered XML using a relational database system”.SIGMOD 2002, pp.204-215,June, 2002.

[17] Wu, X., Lee, M. L., & Hsu, W. “A Prime Number Labeling Scheme for Dynamic Ordered XML Trees. International Conference on Data Engineering”.ICDE 2004, pp.66-78, April, 2004.

[18] Zhang, C., Naughton, J., Dewitt, D., Luo, Q.,& Lohman, G. “On supporting containment queries in relational database management systems”.ACM Sigmod Record, Vol.30, No.2,pp.781-785, June, 2001.

[19] Bruno, N., Koudas, N., & Srivastava, D. “Holistic twig joins: optimal XML pattern matching”.SIGMOD 2002, pp.310-321, June, 2002.

[20] Wang, H., Park, S., Fan, W., & Yu, P. S. “ViST: A Dynamic Index Method for Querying XML Data by Tree Structures”.SIGMOD 2003, pp.110-121,June, 2003.

[21] Rao, P., & Moon, B. “PRIX: indexing and querying XML using prufer sequences”.International Conference on Data Engineering(ICDE 2004),pp.288-299. March, 2004

[22] Chen, Q., Lim, A., & Ong, K. W. “D(k)-index: an adaptive structural summary for graph-structured data”.SIGMOD 2003, pp.134-144, June,2003.

[23] Goldman, R. , & Widom, J. “Dataguides: enabling querying formulation and optimization in semistructured database”.VLDB 1997, pp.436-445, July 1997.

[24] Kaushik, R., Bohannon, P., Naughton, J. F., &Korth, H. F. “Covering indexes for branching path queries”.SIGMOD 2002, pp.133-144, June,2002.

[25] Wang, W., Jiang, H., Wang, H., Lin, X., Lu, H., &Li, J. “Efficient processing of xml path queries using the disk-based F&B index”.VLDB 2005,pp.145-156, August, 2005.

[26] Bruno N, Koudas N, Srivastava D. “Holistic twig joins: optimal XML pattern matching”.SIGMOD 2002, pp.310-321, June, 2002.

[27] Mohammad, S. A, Martin, P. “Index structures for xml databases”. Advanced Applications and Structures in XML processing: Label Streams,Semantics Utilization and Data Query Technologies, pp.98-124, March, 2011.

[28] Li, C., & Ling, T. W. “QED: A novel quaternary encoding to completely avoid re-labeling in XML updates”.Proceedings of the 14th(2005)ACM international conference on Information and knowledge management,pp.501-508, October, 2005.

[29] Xu, L., Ling, T. W., Wu, H., & Bao, Z. (2009). “DDE:from dewey to a fully dynamic XML labeling scheme”.SIGMOD 2009, pp.719-730, June,2009.

[30] Mohammad, S., & Martin, P. “LLS: level-based labeling scheme for XML databases”.Conference of the Centre for Advanced Studies on Collaborative Research, pp.115-127, November,2010.

[31] Ko, H. K., & Lee, S. K. “A binary string approach for updates in dynamic ordered xml data”.IEEE Transactions on Knowledge & Data Engineering,Vol.22, No.4, 602-607, April, 2010.

[32] Li, C., Ling, T. W., & Hu, M. “Efficient Processing of Updates in Dynamic XML Data”.International Conference on Data Engineering(ICDE 2006),pp.13-13, April, 2006.