Transmission Capacity Analysis for Linear VANET under Physical Model

Xinxin He , Hang Zhang, Weisen Shi, Tao Luo, Norman C. Beaulieu

Beijing Laboratory of Advanced Information Networks, Beijing Key Laboratory of Network System Architecture and Convergence, Beijing University of Posts and Telecommunications, Beijing 100876, China

I. INTRODUCTION

Vehicular ad hoc networks (VANETs) have attracted increasing attention from governments, the academia and industries because of the emergence of intelligent transport systems(ITSs). Different paradigms for information communication propose different types of vehicle infrastructure integration, including vehicle-to-infrastructure (V2I) communication, vehicle-to-vehicle (V2V) communication and a hybrid mix of both V2I and V2V [1].VANETs assume that all or a subset of all vehicles are equipped with radio devices, treat driving vehicles as moving wireless nodes and moving routers, and form a wide range of wireless mobile networks that take advantage of brief communication amongst vehicles.

Several projects and standards have been successfully deployed for VANETs. In 2003,the Federal Communications Commission of the US set an allocation of 75 MHz between 5.850 and 5.925 GHz for dedicated shortrange communication (DSRC) to meet the wireless communication demand, and the wireless communication capabilities defined by the standard are within a 1 km range in typical highway scenarios [2]. Several national collaboration projects, such as the European DRIVE-C2X and the Japanese Internet-ITS,have also been implemented. In 2004,IEEE802.11p [3] (also referred to as wireless access in vehicular environments, WAVE)was standardised to the physical layer (PHY)and medium access control (MAC) layer of VANETs for communication. This standard inherits many properties of IEEE 802.11 but defines enhancements to 802.11 for adaptability to the vehicular environment. The upper layers are standardised by the IEEE 1609 protocol family [4], in which 1609.2 addresses security services for management messages and applications, while 1609.3 focuses on issues of transport and network layers and defines a WAVE short message protocol for safety applications.

In this paper, the authors built our model on the basis of a highway scenario, and the proposed model mimics the CSMA/CA used in IEEE802.11p from the perspective of geometric relationship between simultaneous transmitters.

The applications in VANETs deliver functions and services mainly in three areas: traffic safety, consumer convenience and traffic operation. The most important area comprises the safety applications, in which periodic messages (e.g. location, speed, traffic and alert messages) may be exchanged to help drivers navigate and adjust their vehicles to avoid dangerous situations [5–7]. Transport efficiency and information/ entertainment applications are directly used by the users.These applications include enabling of voice communication amongst vehicles, analysis of exemplarily enhanced route guidance and navigation, and green light optimal speed advisory. Traffic congestion inevitably occurs during road emergencies. Hence, the frequent use of the aforementioned applications for communication or entertainment continues to increase.However, network capacity is limited, and not all messages can be delivered effectively.Therefore, the research on VANET capacity is crucial.

Gupta and Kumar [8] initially investigated the network capacity of wireless ad hoc networks and proposed two possible models,namely, the protocol model and the physical model, for the successful reception of transmission. Many other studies have been conducted to improve the capacity of wireless ad hoc networks under the protocol model or physical model. In the present work, we investigate the network capacity of VANETs under the PHY model. However, unlike common ad hoc wireless networks, VANETs have certain fundamental characteristics that make their network capacity research considerably challenging. For instance, in studies on ad hoc wireless networks, the nodes are distributed on the plane or in a 2D observation window,while in VANET research, the nodes are distributed along roads or highways. In addition,most of the MAC protocols considered in the studies on ad hoc wireless networks are based on ALOHA, which is too basic to model the enhanced distributed channel access (EDCA)equipped by 802.11p VANETs. In the present study, we build a 1D line model to discuss the capacity of VANETs in a highway environment. Considering that the effect of EDCA on VANETs is almost the same as that of carrier sense multiple access with collision avoidance(CSMA/CA) [9], we set our transmission scheme to mimic CSMA/CA and describe it from the perspective of the geometric relationship amongst simultaneous transmitters. The aggregate interferences from all simultaneous transmitters are also considered to discuss transmission and outage probabilities. The contributions of this study are threefold. Firstly, we intuitively describe the clear channel assessment (CCA) mechanism in CSMA/CA and then analyse the attempted transmission probability of each road segment, as well as the maximum intensity of active transmitters,including their theoretical values. Secondly, given that achieving an exact calculation seems infeasible, we derive bounds for outage probability and the upper bound of the transmission capacity of the networks under Rayleigh fading. Finally, we use the MATLAB simulator to implement the model and validate our theoretical results.

The remainder of this paper is organised as follows. Section 2 reviews previous works about transmission capacity in both ad hoc networks and VANETs. Section 3 introduces the system model. Section 4 presents the intuition of the main results. Section 5 provides the theoretical analysis about VANET transmission capacity. Section 6 presents the simulations and analytical results, and Section 7 concludes the paper.

II. RELATED WORK

Outstanding results on wireless ad hoc network capacity, which is an important issue in network information theory, have been presented. Gupta and Kumar [8] proposed that a typical time-slotted protocol with adjacent neighbour communication can achieve a sum network throughput which scales asOn the basis of stochastic geometry theory, Baccelli et al. [11] showed that transport capacity, defined as the number of bit-metres occupying a unit area for a network of nodes, is proportional towhere λ is the density of transmitting nodes. Weber et al.[12–13] defined transmission capacity as the product between the maximum density of successful transmissions and the corresponding data rate with a constraint on outage probability. They also discussed transmission capacity with channel fading and proved that channel fading can significantly reduce transmission capacity in the absence of channel-state information. Other recent works [14–16] have improved these transmission capacity theories in different scenarios and environments. However, almost all MAC protocols investigated are based on TDMA or ALOHA, which are not capable of realistically modelling MAC protocols equipped with 802.11p VANETs. In addition, existing studies have only proposed asymptotic descriptions of network capacity related to the number of nodes in a network.In ad hoc network research, the topology and behaviour of nodes are always described as a 2D Poisson process in a plane; this approach cannot be directly applied in VANET research.Given that the vehicles (nodes) in VANETs are distributed along roads or highways, the topologies are modelled as lines or grids.

Considering that the vehicles in VANETs must move along roads or highways and their common transmission range is longer than the road or highway width, the model can be built as a 1D linear road or a grid plain to discuss a realistic network capacity for VANETs. Several works have been conducted on the basis of such models [17–20]. In [17], the network geometry of urban vehicular networks was described as a scalable grid, and the asymptotic throughput capacity performance was intuitively analysed. In [18], the network throughput capacity in a downtown grid scenario was proposed aswhen nodes were uniformly distributed along roads. However,in these two works, the asymptotic theoretical results were derived by utilising the scaling laws under a protocol model that cannot compute the exact transmission capacity in terms of system parameters for general cases. A few papers have presented physical models for VANET transmission capacity analysis [19–21]. In [19], the authors obtained the transmission capacity of a linear VANET on the basis of stochastic geometry. Slotted ALOHA was used as the access scheme, and the transmitters were assumed to form a Poisson process.In [20], the authors proposed both the lower and upper bounds of transmission capacity for highway VANETs with the CSMA/CA access scheme. However, both bounds were only asymptotic values, and the PHY layer model was unrealistic. For instance, the effect of interferences from all simultaneous transmitters and small-scale fading was ignored; such effect may significantly influence transmission capacity. In [21], network capacity was defined as the number of simultaneous transmitters in a linear VANET. The authors evaluated the spatial reuse of a VANET using the CSMA/CA scheme and proved that the maximal number of simultaneous transmitters converges to the upper bound. Nevertheless, the value of the upper bound was simply estimated via simulations. Similar to that in [20], interference was considered only from two neighbour nodes, and path-loss was considered without small-scale fading. Therefore, the estimation of VANET capacity was not adequately valid.

III. SYSTEM MODEL

3.1 Scenario model

Our model (Fig. 1) is built on the basis of a highway scenario with sufficiently great length. We assume that each vehicle is equipped with an 802.11p/1609.4 IEEE compliant radio transceiver. Through this radio interface, vehicles can communicate with one another without affecting roadside infrastructure. In the IEEE 802.11p standard, the transmission range of a vehicle is approximately 500 m to 1,000 m, which is longer than the highway width. Therefore, we simplify the 2D strip-shaped network area into a 1D straight line. In this scenario, all vehicles move independently along the straight line. We consider the concurrent existence of unicast flows in the network and the spatial closeness of the source and destination vehicles of eachunicast flow.

All transmitting vehicles are assumed to share a same transmission data-rate R and a same transmission powerand each transmitter is equipped with a dedicated receiver within its transmission range. The propagation channel is modeled as a product of the largescale path-loss and small-scale Rayleigh fading given by

where d denotes the spread distance,denotes the path-loss exponent, and H denotes the channel power gain which is exponentially distributed.

3.2 Communication model

According to different priorities, application messages are categorised into four different queues in the 802.11p EDCA mechanism,and each queue fulfils a classical CSMA/CA mechanism with different parameters [9]. For simplicity, data packets can be assumed to have the same priority and length as those in transmission capacity research. Thus, for our work, the task of modelling EDCA becomes the task of modelling the traditional CSMA/CA.

In the CSMA/CA protocol, a candidate node senses the channel before sending messages. The messages are transferred immediately when a free signal is tested. Whether the channel is busy is evaluated by a system called clear channel assessment (CCA), which is embedded in CSMA/CA. Several types of CCA modes can be used to decide channel states.This study considers CCA mode 1, in which CCA should report a busy medium upon detecting total energy above the energy detection threshold. Given the limitation of CCA, the minimum distance between every two transmitters must be exceeded to guarantee proper transmission. Thus, CCA limits the number of simultaneous transmitters in the space and the number of frames sent per second.

3.3 Definitions of outage probability and transmission capacity

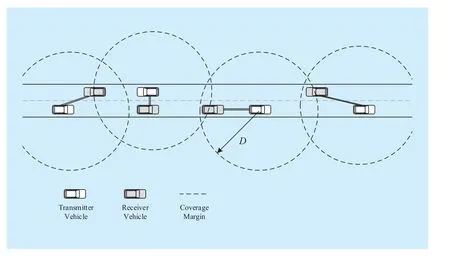
Fig. 1 Basic highway scenario

IV. INTUITIVE ANALYSIS

In this section, we present the key intuition of the main result of this study. As mentioned above, the CSMA/CA protocol limits the number of simultaneous transmitters that can be used to calculate the maximal number or density of simultaneous transmitters over a linear road. We consider an extreme case, in which the distribution of transmitters should satisfy two special attributes. Firstly, all transmitters are assumed to be in the positions where the total received power of interferences is no more than the threshold. Secondly, the total power of interferences in any position between any two neighbour transmitters is higher than. This attribute guarantees that no other transmitter can be added between any two existing neighbour transmitters. In addition, any existing transmitter can no longer find other desirable positions with low total interferences.This specific distribution comprises maximal simultaneous transmitters over the linear road.

The minimal distance between two consecutive transmitters is denoted asand in order to simplify the calculation, the smallscale fading of the propagation channel is ignored in this intuitive analysis. Under uniform distribution, the total interference power I detected by anyone of simultaneous transmitters is given by

where Kmdenotes the maximal value of K.As the sum of harmonic series is hard for calculating in (5), we use an attribute of convex function to derive a closed-form expression:

This upper bound limits the maximal value of transmission capacity. It is worth noting that this transmission capacity is not only determined by its maximal density of simultaneous transmitters but also by the outage probability.In next section, we will analyze and derive the outage probability of the transmission and the concrete and precise expression of VANET transmission capacity considering both largescale path-loss and small-scale Rayleigh fading.

V. NETWORK TRANSMISSION CAPACITY ANALYSIS

For VANET, the analysis of its transmission capacity is important both in theory and application. In this section, on the basis of the intuitive analysis aforementioned, we first propose a transmission scheme mimics the CSMA/CA,and derive the attempted transmission probability of each road segment and the maximum intensity of active transmitters. After that, we derive the outage probability and transmission capacity of the network under Rayleigh fading.

5.1 Active transmission scheme

As shown in Fig. 2, we consider an infinite line-like highway layout and divide the line intoequal road segments of lengthwhere d is the average distance between each transmission group. We assume that a pair of vehicles can communicate only when they are on the same road segment at the same time slot. With all vehicles using the single-channel transceiver,a maximum of one transmission can occur on each road segment at each time slot.

As the proposed model mimics the CCA mode 1 mechanism of CSMA/CA, the sum of the signals from all the other simultaneous transmitters is considered to detect if the medium is idle or busy. A vehicle is allowed to transmit when the total measured interference is no

5.2 Maximum intensity of active transmitters

In this work we treat the road as in finite and ignore the endpoints’ impacts. We assume the reference transmission group is on segmentas shown in Fig. 2. With the length of the line is sufficiently great, it can be supposed that there are bothsimultaneous active transmitters on each side of the reference node on highlighted green segments. Without loss of generality,

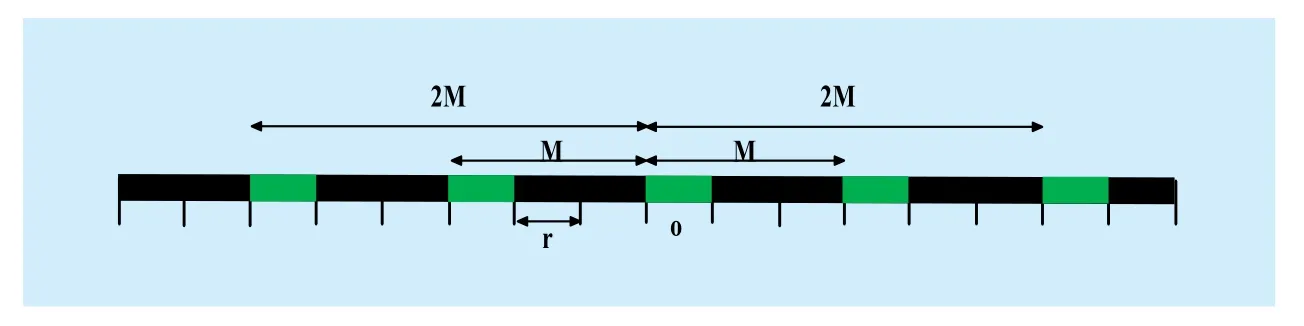
Fig. 2 A line-like highway layout

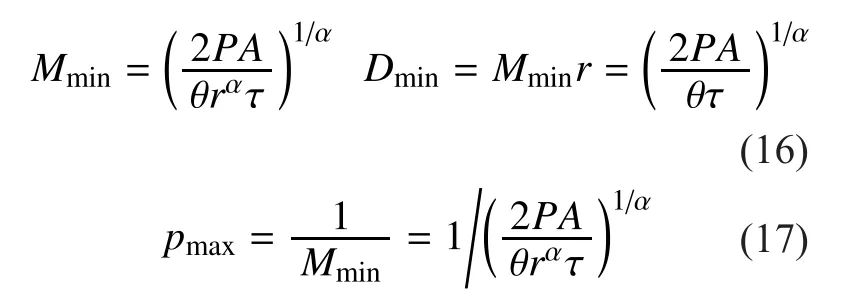
Theorem 1.The maximum density of simultaneous active transmitters over the line is given by

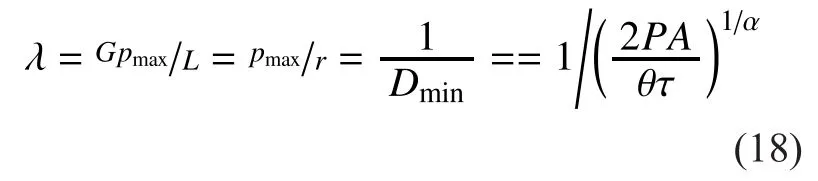
5.3 Transmission capacity analysis under rayleigh fading

VI. SIMULATION RESULTS

In validating our upper bound of network transmission capacity, we use the MATLAB simulator to build a highway environment.The highway is modelled as a line with a distance of 4 km, and vehicle distribution and data transmission mechanisms are simulated in 802.11p. All vehicles in these simulations transmit frames to a neighbour with a constant bit rate; the moving pattern of all potential transmitting vehicles is described as the classic car-following model [23] which claims that the mean distance X between any two neighbour vehicles on a linear road follows a log-normal distribution parameterized byand

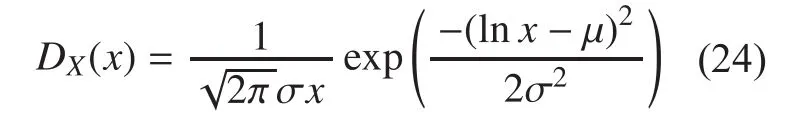
The car-following model is mainly used to simulate the realistic behaviour of vehicles in VANETs. The instantaneous distribution of all transmitters in any timeslot is obtained from the model. We only calculate the transmission that occurs in the 2 km portion of the central part of the road to eliminate the effects of less-interfered transmitters located near the endpoints of the linear road. Although transmitters out of this range still transmit data and influence the transmitters in the central part, their transmitted data are not involved in total throughputs. The capacity is computed as the average spatial density of successful transmissions in the networks. The intensity of transmitters is computed as the total number of simultaneous transmitters at a given time during the simulation.

Fig. 3 shows the simulation results of the average transmission capacity over the 4 kmlong central part of the road and the two upper bounds proposed in this study and in [21].The dash-dotted curve with an error bar and the circle-dotted curve depict the average and maximal values of transmission capacity under Rayleigh fading as well as the relationship between them and the distance of neighbor vehicles, respectively. In this study, we set

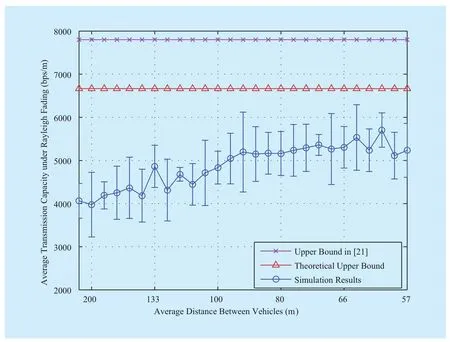
Fig. 3 Average transmission capacity and upper bound under Rayleigh fading

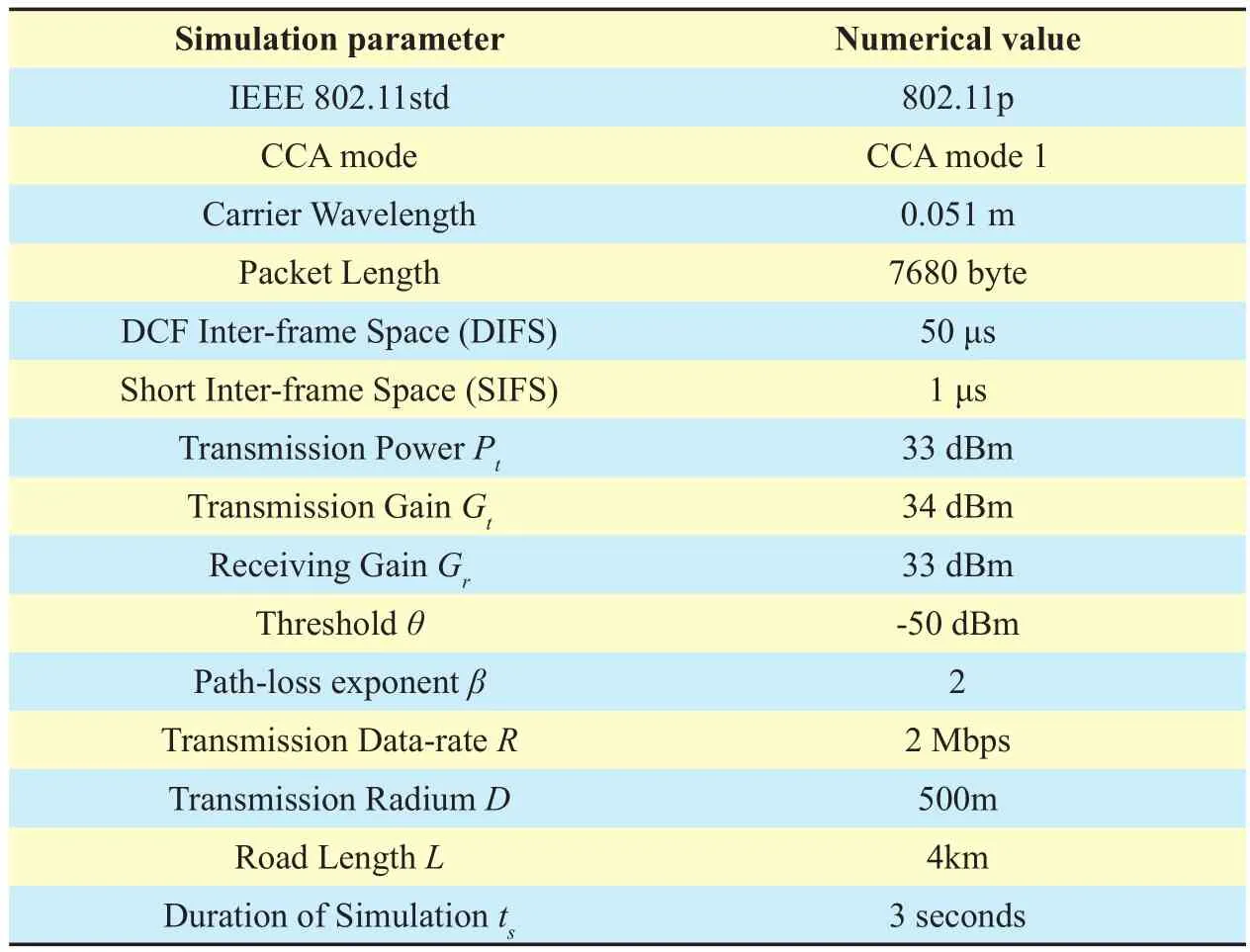
Table I Simulation parameters

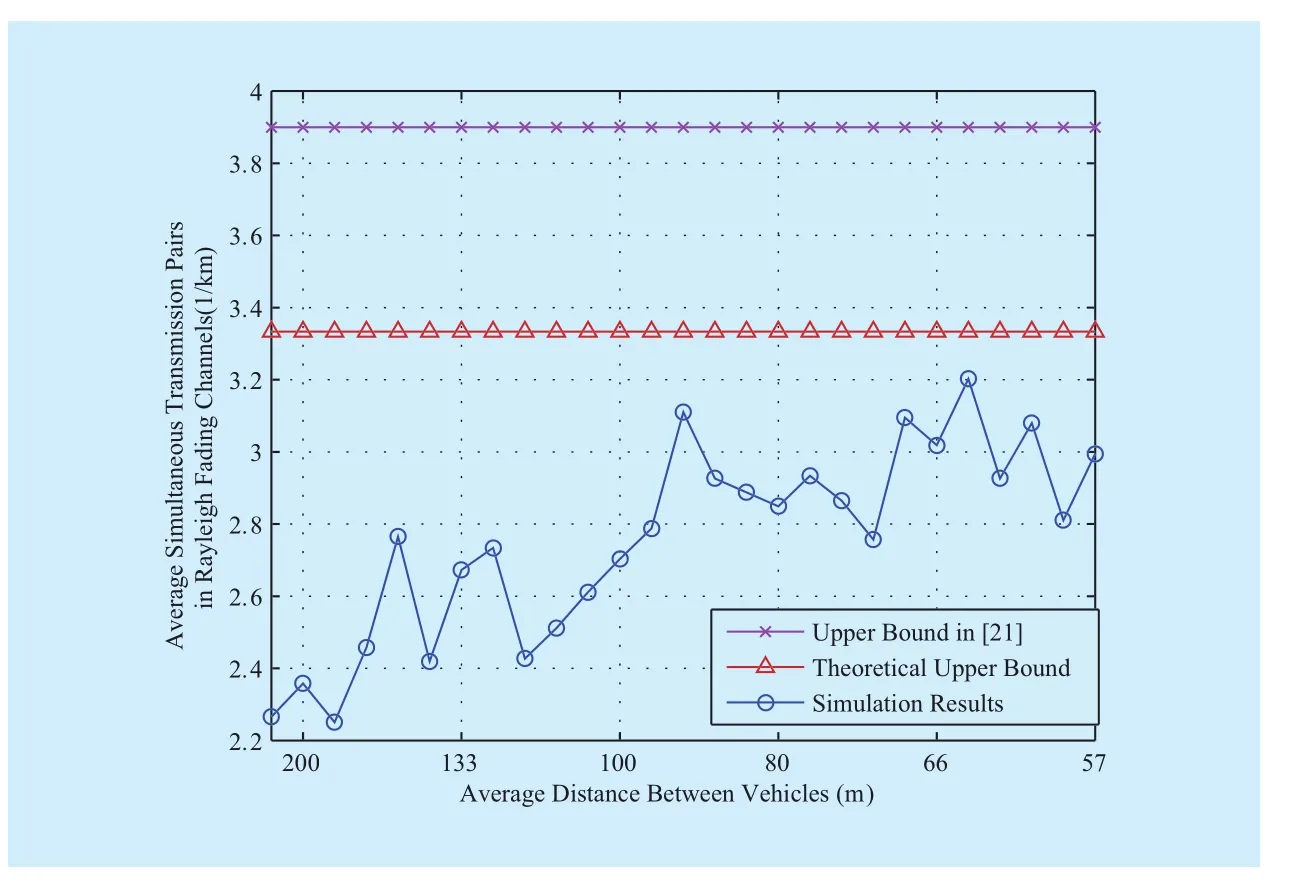
Fig 4 Average density of simultaneous transmitters and maximal density under Rayleigh fading

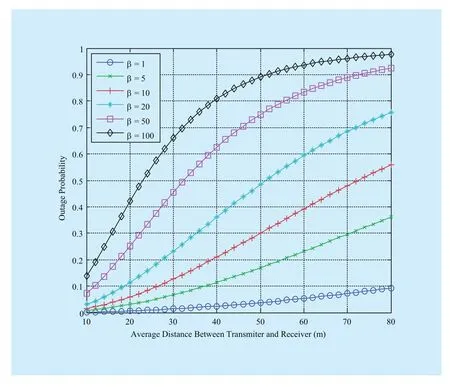
Fig. 5 Outage probability vs. average distance between each transmission group under Rayleigh fading

multaneous transmitters (circle-dotted curve),and the upper bound (triangle-dotted line) is calculated by solving Equation (23) without considering transmission data rate. Our result still outperforms the result (cross-dotted line) in [21]. This difference in the performance of the two bounds is discussed as follows. Firstly, the interference in our model originates from all simultaneous transmitters,whereas the interference in [21] originates from only two adjacent transmitters and is multiplied with an estimated constant from simulations. Moreover, the small-scale fading considered in our channel model is ignored in[21]. In [21], the authors did not consider the outage probability in transmission that leads to inaccurate results. As shown in (3) and (19)in the present work, transmission capacity is larger than the real value without outage probability. Therefore, our bound is more accurate and constrains simulation results better compared with the bound in [21].

We also present the numerical results on the basis of the preceding analysis and offer our interpretation. In Fig. 5, the outage probability versus distance amongst each transmission group under Rayleigh fading is illustrated with different threshold. Generally, when the distancebetween a transmitter and a receiver increases, the outage probability also increases. As other parameters are fixed, the increased signal transmission distance reduces the received signal power, which is represented as a decline in signal-to-interference ratio.The outage probability increases with increasing. Fig. 6 illustrates the opposite change trend of Fig. 5, i.e. the transmission capacity of the upper bound decreases with the increasing distance between the transmitter and the receiver. Therefore, a large distance increases outage probability, in which case transmission capacity decreases.

VII. CONCLUSION

In this paper, we built our model on the basis of a highway scenario, and the proposed model mimics the CSMA/CA used in IEEE802.11p from the perspective of geometric relationship between simultaneous transmitters. After intuitive describe the CCA mechanism, we derive the upper bound on network capacity of VANET under physical model. Finally, we use the MATLAB simulator to perform our model and validate that the theoretical result offers a well bound on the network capacity.

ACKNOWLEDGEMENTS

This work is supported in part by the National Natural Science Foundation of China under Grant No. 61271184 and 61571065.

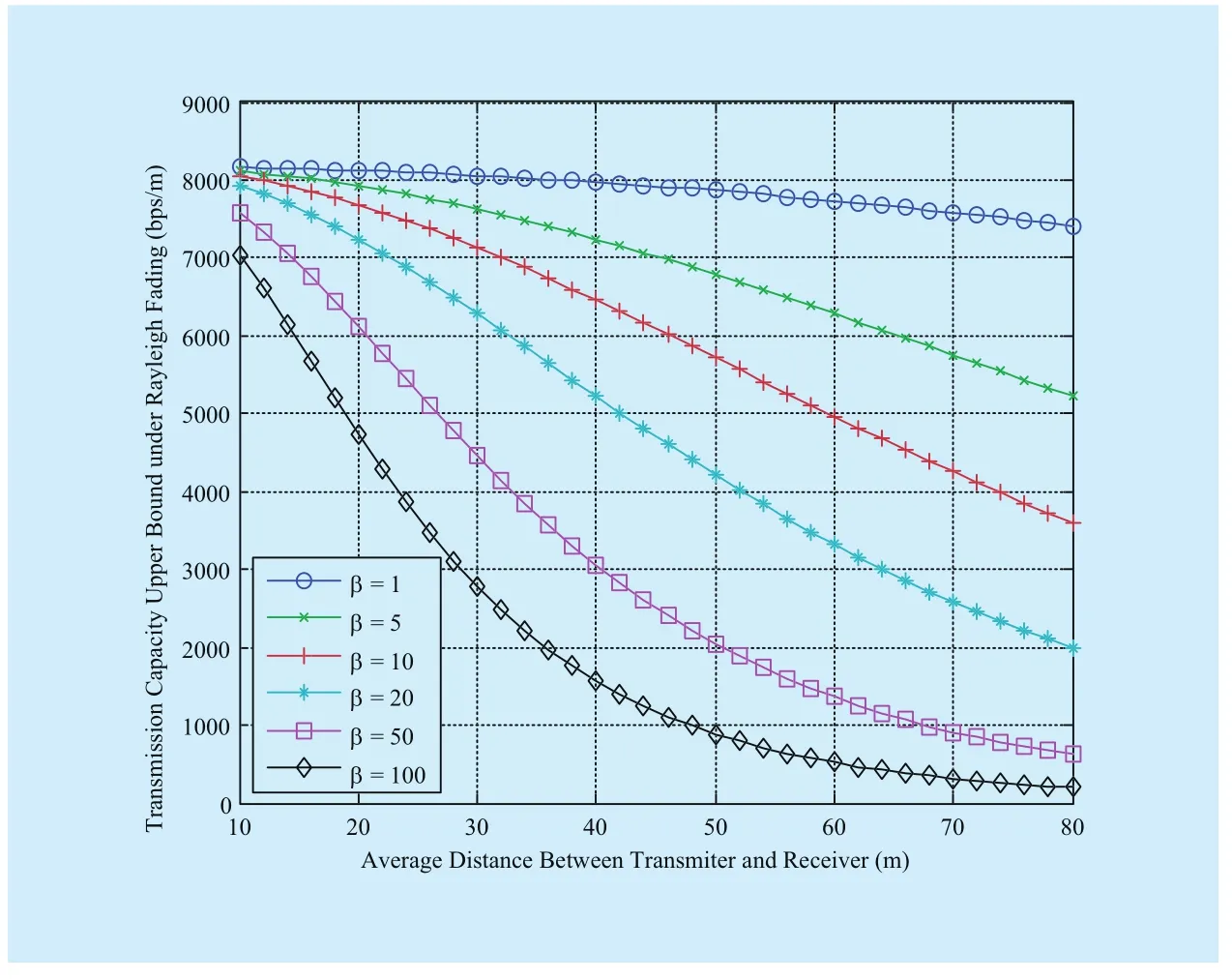
Fig. 6 Transmission capacity upper bound vs. average distance between each transmission group

[1] F. Bai, and B. Krishnamachari. “Exploiting the Wisdom of the Crowd: Localized, Distributed Information-Centric VANETs.”IEEE Communications Magazine, vol. 48, no.5, pp 139-146, May, 2010.

[2] J. B. Kenney, “Dedicated Short-Range Communications (DSRC) Standards in the United States.”Proceedings of the IEEE, vol. 99, no. 7, pp 1162-1182, June, 2011.

[3] Chair: Wayne Fisher editor: L. Armstrong, Status of project IEEE 802.11 task group p. wireless access in vehicular environments (wave). http://grouper. ieee. org / groups / 802//11/Reports/tgp_update.htm. 2010.

[4] IEEE Draft Guide for Wireless Access in Vehicular Environments (WAVE) – Architecture. IEEE P1609.0/D7.0, vol., no., pp.1-77, Aug, 2013.

[5] H. Hartenstein, and K. P. Laberteaux, “VANET:Vehicular Applications and Inter-Networking Technologies”,Chichester: Wiley, 2010.

[6] X. He, W. Shi, and T. Luo. “Survey of Cognitive Radio VANET.”Ksii Transactions on Internet &Information Systems, vol. 8, no.11, pp 3837-3859, Nov, 2014.

[7] M. I. Hassan, H. L. Vu, T. Sakurai, “Performance Analysis of the IEEE 802.11 MAC Protocol for DSRC Safety Applications,”Vehicular Technology, IEEE Transactions on, vol.60, no.8, pp 3882-3896, Oct. 2011.

[8] P. Gupta, and P. R. Kumar. “The capacity of wireless networks.”IEEE Transactions on Information Theory, vol. 46, no. 2, pp 388-404, March, 2000.

[9] J. R. Gallardo, D. Makrakis, H. T. Mouftah, “Performance Analysis of the EDCA Medium Access Mechanism over the Control Channel of an IEEE 802.11p WAVE Vehicular Network,”Communications, 2009. ICC ‘09. IEEE International Conference on, vol., no., pp 1-6, 14-18, June, 2009.

[10] Franceschetti, Massimo, et al. “Closing the Gap in the Capacity of Wireless Networks Via Percolation Theory.”IEEE Transactions on Information Theory,vol. 53, no. 3, pp 1009-1018, February, 2007.

[11] Baccelli, François, B. Blaszczyszyn, and P. Mühlethaler. “An Aloha protocol for multihop mobile wireless networks.”IEEE Transactions on Information Theory, vol. 52, no. 2, pp 421-436, February, 2006.

[12] S. P. Weber, X. Yang, J. G. Andrews, et al. “Transmission capacity of wireless ad hoc networks with outage constraints.”IEEE Transactions on Information Theory,vol. 51, no. 12, pp 4091-4102, November, 2006.

[13] S. P. Weber, J. G. Andrews, and N. Jindal. “The Eff ect of Fading, Channel Inversion, and Threshold Scheduling on Ad Hoc, Networks.” IEEE Transactions on Information Theory, vol. 53, no.11, pp 4127 - 4149, November, 2007.

[14] Franceschetti, Massimo, et al. “Closing the Gap in the Capacity of Wireless Networks Via Percolation Theory.”IEEE Transactions on Information Theory,vol. 53, no. 3, pp 1009-1018, February, 2007.

[15] V. P. Mhatre, C. P. Rosenberg, and R. R. Mazumdar. “On the Capacity of Ad Hoc Networks Under Random Packet Losses.”Information Theory IEEE Transactions on, vol. 55, no. 6, pp 2494-2498, May, 2009.

[16] S. P. Weber, and J. G. Andrews. “Transmission capacity of wireless networks.”Foundations &Trends® in Networking, vol. 5, no. 12, pp 3593 -3604, January, 2012.

[17] Lu, Ning, et al. “Capacity and delay analysis for social-proximity urban vehicular networks.”Proceedings - IEEE INFOCOM, pp 1476-1484, 2012.

[18] M. Nekoui, A. Eslami, H. Pishro-Nik, “Scaling Laws for Distance Limited Communications in Vehicular Ad Hoc Networks,”Communications,2008. ICC ‘08. IEEE International Conference on,pp. 2253-2267, 2008.

[19] H. Pishro-Nik, A. Ganz, D. Ni. “The capacity of vehicular ad hoc networks” ,Proc.allerton Conf,pp 267 – 272, 2008.

[20] P. Jacquet, and P. Muhlethaler. “Mean Number of Transmissions with CSMA in a Linear Network.”Vehicular Technology Conference, 1988,IEEE 38th, pp 1-5, 2010.

[21] A. T. Giang, A. Busson, D. Gruyer, et al. “A pack-ing model to estimate VANET capacity” ,Wireless Communications and Mobile Computing Conference, pp 1119-1124, 2012.

[22] S. P. Weber, and J. G. Andrews. “Transmission Capacity of Wireless Ad Hoc Networks With Successive Interference Cancellation.” IEEE Transactions on Information Theory, vol. 53, no.8, pp 2799-2814, August, 2007.

[23] M. Brackstone, and M. Mcdonald. “Car-following: a historical review.” Transportation Research Part F Traffic Psychology & Behaviour, vol. 2, no.4, pp 181-196, December, 1999.