Statistical Modeling of the High Altitude Platform Dual-Polarized MIMO Propagation Channel

Mingchuan Yang , Shuo Zhang , Xinye Shao , Qing Guo , Wenyan Tang

1 Communication Research Center, Harbin Institute of Technology, Harbin, 150080, China.

2 Instrument Science and Technology postdoctoral Station, Harbin Institute of Technology

* The corresponding author, Email: mcyang@hit.edu.cn

I. INTRODUCTION

For the past few years, with the rapid development of Chinese railway, an increasing number of passengers are expecting to enjoy smooth Internet access based on wireless local area networks (WLAN) [1]. Thus, the demand becomes stronger for high-speed trains to provide digital, wireless mobile and broadband integrated services. If the traditional cellular mobile system is applied, the signal has to switch frequently between different cellular when the train is traveling along the railway. Then efficient and complex hand off algorithms need to be developed, and the cost and complexity of the system will increase.

Currently, a novel solution is to adopt high altitude platform technique. High altitude platform utilizes airship which locates at 17-22km to be the “aerial base station” [2-4]. And it combines the advantages of both the satellite communication system and the terrestrial cellular mobile communication system. On one hand, it does not need many terrestrial infrastructures; On the other hand, it has characteristics of large coverage area, low propagation delays and broadband capability,and these characteristics make HAP suitable to provide communication service for high speed mobile terminal [5-7]. Modeling the wireless communication channel is the most fundamental step to develop the HAP communication system, and up to now, there are much research setting up channel models for HAP communication system [8, 9]. Among these research, most of them are single-input and single-output channel models based on first-order three-state Markov chain, which describe channel characteristics under typical different environments. Their main limit is that they neglect to consider comprehensively both the channel temporal characteristics(Doppler fading, shadowing) and the spatial characteristics during the fading process. And at the same time, they lack detailed analysis of the factors that influence the channel capacity.Thus, in terms of HAP system, it is urgent to put forward a comprehensive channel model which can describe its spatiotemporal domain characteristics.

The appealing gains as well as the occurred problems and challenges, which obtained by satellite MIMO systems, generate a further interest in investigating the applicability of the same principle in HAP systems. In contrast with satellite MIMO system, MIMO HAP system has characteristics of low cost, stable links between platforms, flexible network coverage, etc. Reference [14] emphasizes to analyze adaptive coding and modulation scheme as well as space and platform diversity exploiting in order to increase the reliability of the communication system. And based on multiple HAP constellations, reference [15]analyzes the virtual MIMO technique, proving that the transmit diversity scheme based on space-time block coding (STBC) can decrease the link outage and increase the average spectral efficiency. The above research all adopt spatial diversity technique, and single HAP is assumed as equipped with one antenna, thus multiple HAPs should be launched to form MIMO system. And if single HAP is equipped with multiple antennas, it will be difficult to generate a completely independent fading profile because of the relatively high spatial correlation. Besides, adopting polarization diversity can generate two independently orthorhombic sub-channels on the polarization direction. Thus, it only needs single HAP to consist the MIMO system, which decreases the space and launching cost greatly. However,currently study on the polarization diversity of HAP system is very deficient.

In this paper, a statistical channel model for dual circularly polarized 2×2 MIMO HAP channels is presented. Such model can be real-ized by separately installing a right-hand and a left-hand circularly polarized element on the HAP and the high-speed train. First, the Doppler shift and temporal correlation are considered. Then, the analysis method for the spatial correlation of each sub-channel is designed.And finally, the complete channel modeling process is presented in this paper. Through simulation, the influence pattern of the channel model parameters to the channel capacity is achieved. Besides, the channel model in this paper can expand to distributed MIMO HAP system, whose application field could reach the communication service of remote areas and emergency rescue.

II. SYSTEM SCENARIO

The system scenario of this paper is shown in Fig. 1. A right-hand and a left-hand circularly polarized element are separately installed on single HAP. At the same time, two circularly polarized antennas are also installed on the operational train. Under the above described situation, MIMO HAP channel can be expressed by a 2×2 MIMO channel matrix H=[hij] (i,j=1,2), where hijis the channel gain between transmit antenna (polarization) j and receive antenna (polarization) i. Each channel gain hijcan be expressed as the sum of large-scale fading partand small-scale fading partwhich separately represents shadowing effect of the LOS path and the multipath diffuse.

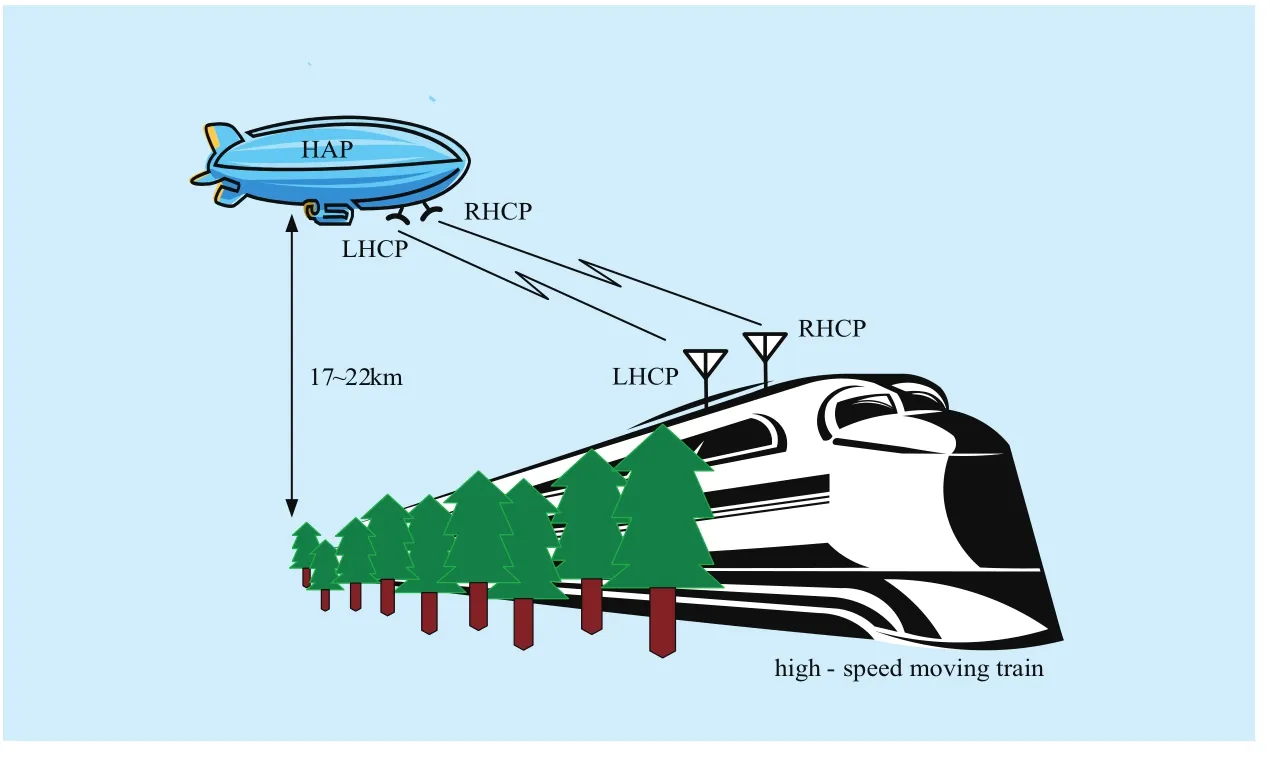
Fig. 1 System scenario of a 2×2 dual polarization MIMO HAP system

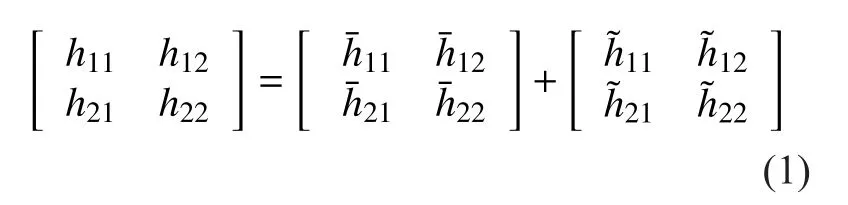
In (1), assume the amplitude of the signal hijmeets the Loo distribution [16]. Where amplitudemeets the logarithmic normal distribution based on parameters (α, ψ), and amplitudemeets Rayleigh distribution with MP multipath power.

As the ITU permitted the use of several frequency bands (including the bands around 2 GHz for IMT-2000) for HAP systems[17], so the working frequency band is set as 2GHz in this paper. Train speed is set as v=300km/h, and the HAP elevation angle is denoted by θ. As the distance between HAP to the ground is relatively low, and transmission delay is much short, the multipath echoes are not significantly spread in time. Thus, the proposed statistical channel model can be considered as narrowband. Because HAP and LMS have many similar characters in channel environment, thus a MIMO HAP channel can be modeled according to the MIMO LMS channel model.

III. DESIGN AND ANALYSIS OF MIMO HAP CHANNEL STATISTICAL MODEL

3.1 Description of temporal correlation

The fading of signal can be divided into fast variations, slow variations and very slow variations these three different rates [18, 19].And channel fading of different rate could be imitated by adopting different sampling rate.Where, parameter lcorris applied to represent the direct signal correlation length. That is to say when the displacement distance at the receiver is less than lcorr, the received signals have certain correlation. Typically, correlation lengths for these slow variations depend on the size of the objects causing the blockages,i.e., several meters. In the channel model, the direct signal slow variations are sampled at v/lcorr, where v is the constant moving rate at the receiver. Additionally, the fast variations are generated with a much higher sampling rate to take into account of the Doppler bandwidth. And the produced uncorrelated samples are spaced λ/F meters, where λ is the wavelength of the transmission signal and F is set as 8 in this paper. So this means that spline interpolation must be applied to the slower variations to make the sum of the matrices in formula (1) established [19].

Another approach of analyzing the temporal correlation of large-scale fading is to let uncorrelated samples (sampled at Fv/λ) pass a low-pass IIR (In finite Impulse Response) filter of one coefficient [14].

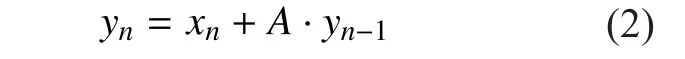
The very slow variations when a mobile terminal travels across large-scale propagation environments are modeled based on a first-order three-state Markov model. In this paper,three typical environments are selected: the first state represents the LOS propagation; the second state denotes the situation, when the signal is partially shadowed by trees; while the third state represents the channel which is completely blocked. And assume lstatemodels the minimum state duration of the channel,which is set as 5m. Besides, statistical parameters of Loo model are assumed constant during each lstatemeters of travelled route. And the following approach is adopted to imitate the states (or Loo model parameters) transfer process: assume the current state is Stand the next state is St+1, and P (i, j) donates the transition probability for state i to state j. First, assume i=1, and variable U which is uniform among(0, 1) is generated randomly. If variable meets

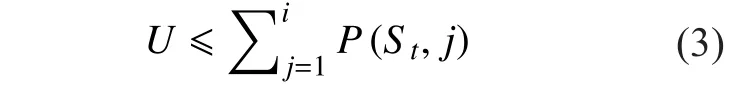
Then the state of the next block T is St+1=i.Otherwise, take i=i+1 into (3) and test again till it meets the condition. Finally, discrete state sequence with interval lstatemeters is obtained through such approach.

From the above analysis, the Markov chain is characterized by state probability vector W and state transition probability matrix P, which are typically obtained from the real propagation channel measurement data. In this paper,the ray tracing approach mentioned in [8] will be adopted to achieve the vector W and matrix P. First, the geographic data along the railway line between Xi’an and Zhengzhou in China is selected. Then, assume trees are distributed randomly along the railway, and import the longitude and latitude data of the railway to generate the digital relief model (as shown in Fig. 2, where the white line represents the railway). The high altitude platform is set to locate 20km in height at the midpoint of the two cities. When the train travels along the railway,if the ray from the train to platform intersects the earth surface (represented by DRM), the channel is in block state. And when the ray is obstructed by the trees along the railway, then the channel is in shadowed state. And if there is a clear view of the platform from the train,then the channel is in the LOS state, Finally,through statistical calculation, the vector W and the matrix P under specific geographic environment are obtained (shown in Table I).Such approach considers the real influencing factors, i.e., geographic environment along therailway, height and location of the HAP, to imitate precisely the visibility between HAP and each site along the railway.

Table I Channel characteristics of three-state markov channel model

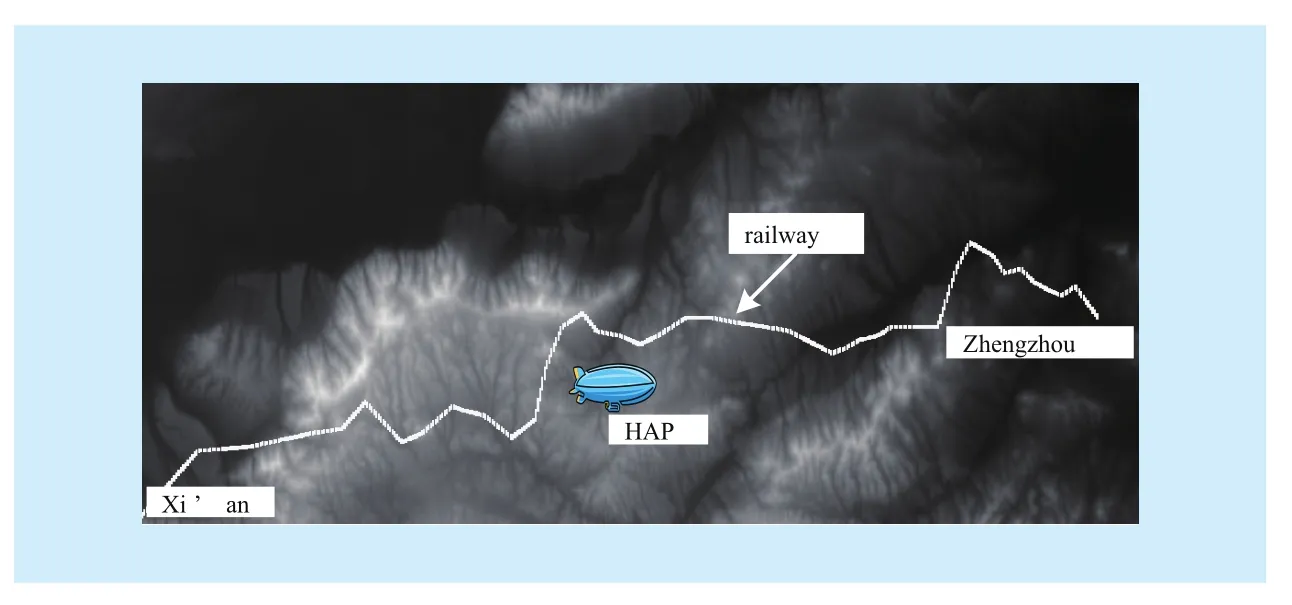
Fig. 2 Generated digital relief model from Xi’an to Zhengzhou in China after importing data

Due to the terminal’s motion, the frequency spectrum of the actual received signal will cause Doppler Effect. In this case, a lowpass low-order Butter worthfilter will be used,which is a quite common assumption in land mobile satellite channels [18, 19].

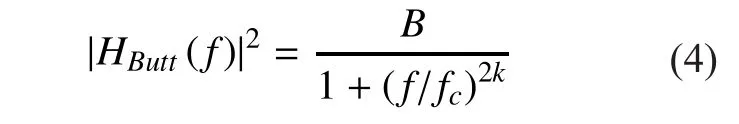
Where, fcis the cutoff frequency and k is the order of the filter. As the standard deviation of the zero-mean Gaussian random variable will change when it passes the filter, thus a multiplicative factor, which is proportional to the inverse of the square root of the filter’s energy, needs to be introduced at its output to compensate for this effect.

In the next step, the phase variations in the direct signal are introduced. These are assumed to be linearly varying giving rise to a constant Doppler spectral line. When the train travels λ/F meters, constant phase increment is given by

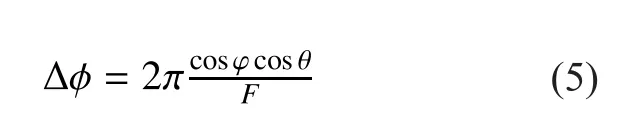
Where, φ and θ being the relative azimuth,with respect respectively to the train route and elevation angles.

3.2 Description of spatial correlation and polarization correlation

The spatial correlation and polarization correlation of each sub-channel in the dual polarized MIMO channel model will in fluence the performance and capability of the MIMO system. The cross-polar transmissions (e.g. from a right-handed circular polarized Tx antenna to a left-handed circular polarized antenna Rx antenna) would not exist according to the ideal situation. But because of the potential depolarization influence from the environment during the transmission process, and the unsatisfactory XPI (cross-polar isolation) of the transmitting and receiving antennas, the cross-polar transmissions will exist in practical situation. Considering a 2×2 dual polarized MIMO channel model described in formula(1), if hij(i,j=1,2) represents the gain of the complex channel, defineas the power gain between polarized antenna i and polarization antenna j, where E[·] donates the expected value. Then we have:

(1) XPDenv=P11/P12represents the depolarization caused by the environment;

(2) XPDant,tand XPDant,rrepresent respectively the depolarization caused the unsatisfactory XPI of the transmitting and receiving antennas;

(3) CPR=P11/P22represents the co-polar ratio, and assume 10log10CPR=0dB, which indicates power of the signals traveling along the two co-polar directions is symmetrical;

In the following formula, Θ designates the dual-polarized MIMO channel for co-located antennas (there are no spatial correlation effects), that is to say it imitates the polarization correlation between each sub-channel and the unbalanced distribution of power during channel depolarization process. And Θ can be considered as the sum of the large-scale fading component () and the small-scale fading component (), which is shown as followed

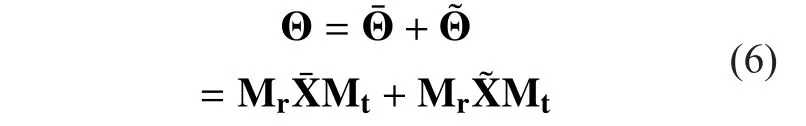
Where, Mrand Mtare respectively the effect of imperfect cross-polar antenna isolation at the transmitter and receiver in the depolarization process. Mrand Mtcan be described as

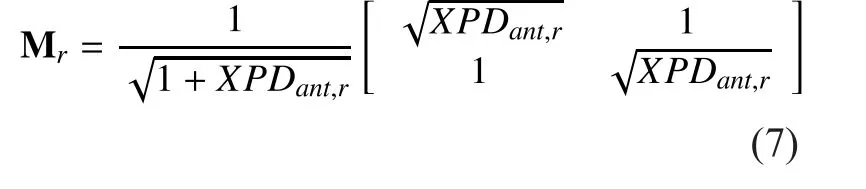
Thus replacing (10), the polarization correlation of the small-scale fading component can be described as

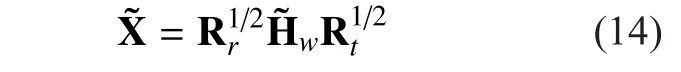
Assume spatial correlation are independent of polarization correlation [21], and H2×2designates the dual-polarized channel matrix combining spatial separation and dual polarization, then H2×2can be decomposed into

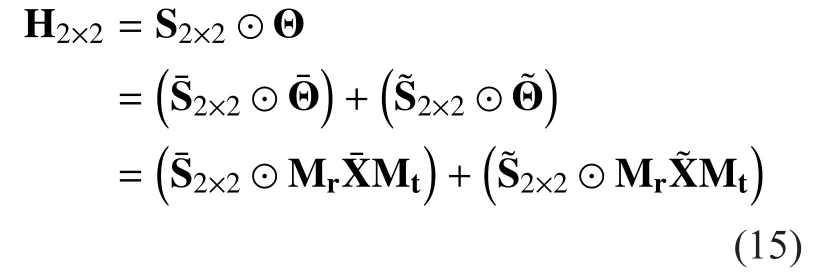
If a 2N×2M dual polarization is considered,the MIMO channel with spatial correlation needs to be equipped with N and M sub-arrays at the transmitting terminal and the receiving terminal respectively. And each sub-array is identical and is made of two orthogonally polarized antennas with certain interval. Then the channel matrix can be described as [22]

3.3 Time series generator of 2×2 MIMO HAP channel

On the basis of the above analysis, a specific time series generator of 2×2 MIMO HAP channel for dual-polarized co-located antennas will be set up, which can be divided into two main parts. For part one, four independent MIMO HAP sub-channel simulation models,respectively representing two co-polar transmission channels and two cross-polar trans-mission channels, are set up with the same approach. And temporal correlation and Doppler Shift are taken into consideration in each sub-channel. For part two, the polarization correlation and power distribution between each sub-channel are analyzed. Below is the specific analysis:

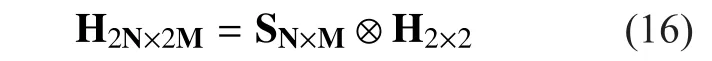
For part one, it can be divided into two steps, the first step is to make use of DRM to imitate the real environment for train traveling from Xi’an to Zhengzhou in China, and state probability vector W and state transition probability matrix P of the Markov chain are generated by ray tracing approach. Then, a discrete state sequence with interval lstatemeters is obtained by adopting (3). Such discrete state sequence can be utilized to select the corresponding parameters of Loo model under different states. As the antennas at link ends are displayed with co-positions, so both polarizations are transmitted via the same link. Thus the four sub-channels can adopt the same discrete state sequence [22].

The second step is to generate the time series of the received signal, which satisfies the Loo distribution. The time series generator of the small scale fading components is as follows [19]: two zero-mean and unit-standard deviation Gaussian series (sampled at vF/λ)in quadrature are passed through a Doppler spread low-pass filter simulating Clarke’s spectrum, as shown in (4). After Doppler shaping, the resulting complex series of the small scale fading components is multiplied by MP.

On the other hand, the lognormal series generator is as follows: an α (dB) mean and ψ (dB) standard deviation Gaussian series is generated. These Gaussian series are then lowpass filtered in order to introduce the temporal correlation, as shown in (2). The series are converted to linear units (lognormal distributed) by computing the antilogarithm, a=10A/20.In the next step, the phase variations in the large scale fading components are introduced,as shown in (5). Finally, the series from the two rails (large and small scale fading components), can be added up to produce a Loo distributed time series, as shown in (1).

The process diagram of comprehensive MIMO HAP sub-channel simulation model is shown in Fig. 3. It completely describes the process for the complex envelope of single-input single-output channel model.

Then for part two, when considering the polarization correlation of each sub-channel, it also can be divided into two main steps:

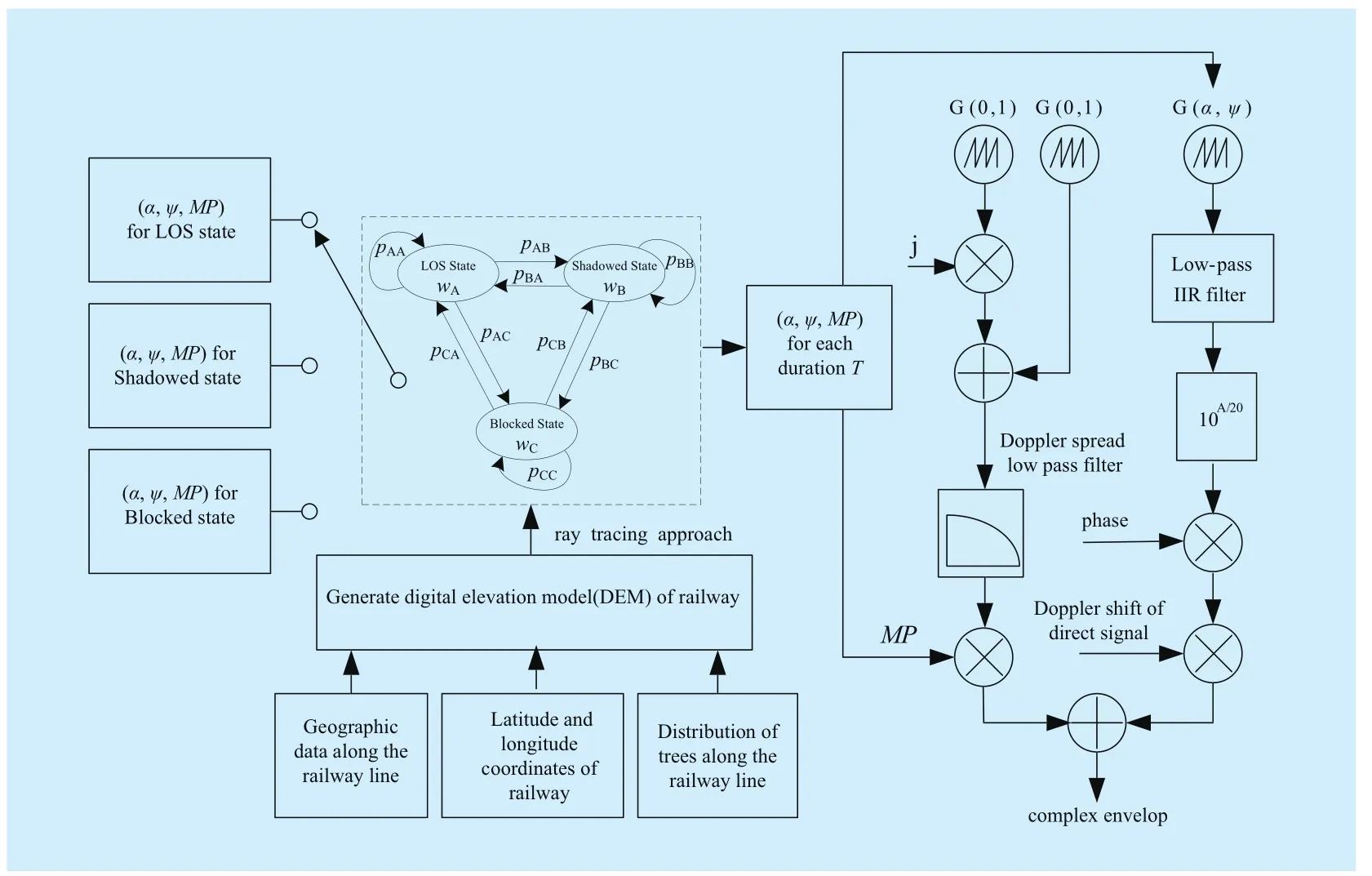
Fig. 3 Process diagram of comprehensive MIMO HAP sub-channel simulation model

The first step is to respectively imitate the polarization correlation of large-scale fading and small-scale fading through (9) and (14).But because the antennas at link ends are displayed with identical positions, so matrix S2×2in (15) is 12×2，which means all its elements equal to 1. So the influence of its spatial correlation is not taken into account.

The second step is to imitate the depolarization influence of the transmission environment as well as the transmitting and receiving antennas through the power distribution of each sub-channel. Below are the two assumptions:

(1) Assume the XPDant,tof the transmitting antenna located at the HAP is close to ∞. Thus we only consider the depolarization influence of the receiving antenna. And XPDant,rwill influence both the large-scale fading and the small-scale fading parts;

(2) The depolarization influence XPDenvcaused by environmental factors will only affects the small-scale fading part.

Based on the above assumptions, a more reasonable power distribution approach is presented by [11]：We assumes symmetry of the co- to cross-polar ratio independently of the reference polarization, hence the power of the small-scale fading component is given by:

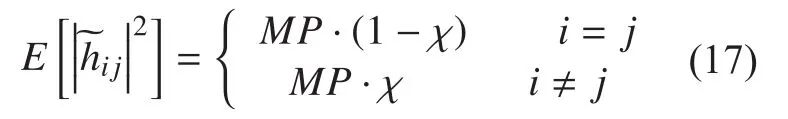
Then the power of the large-scale fading component is given by:

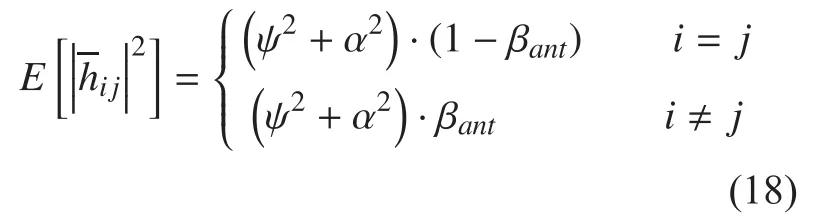
Essentially speaking, such approach changes the power ratio of co-polar transmission to cross-polar transmission and realize the imitation of depolarization mechanism.

IV. SIMULATED RESULTS AND DISCUSSION OF MIMO HAP CHANNEL MODEL

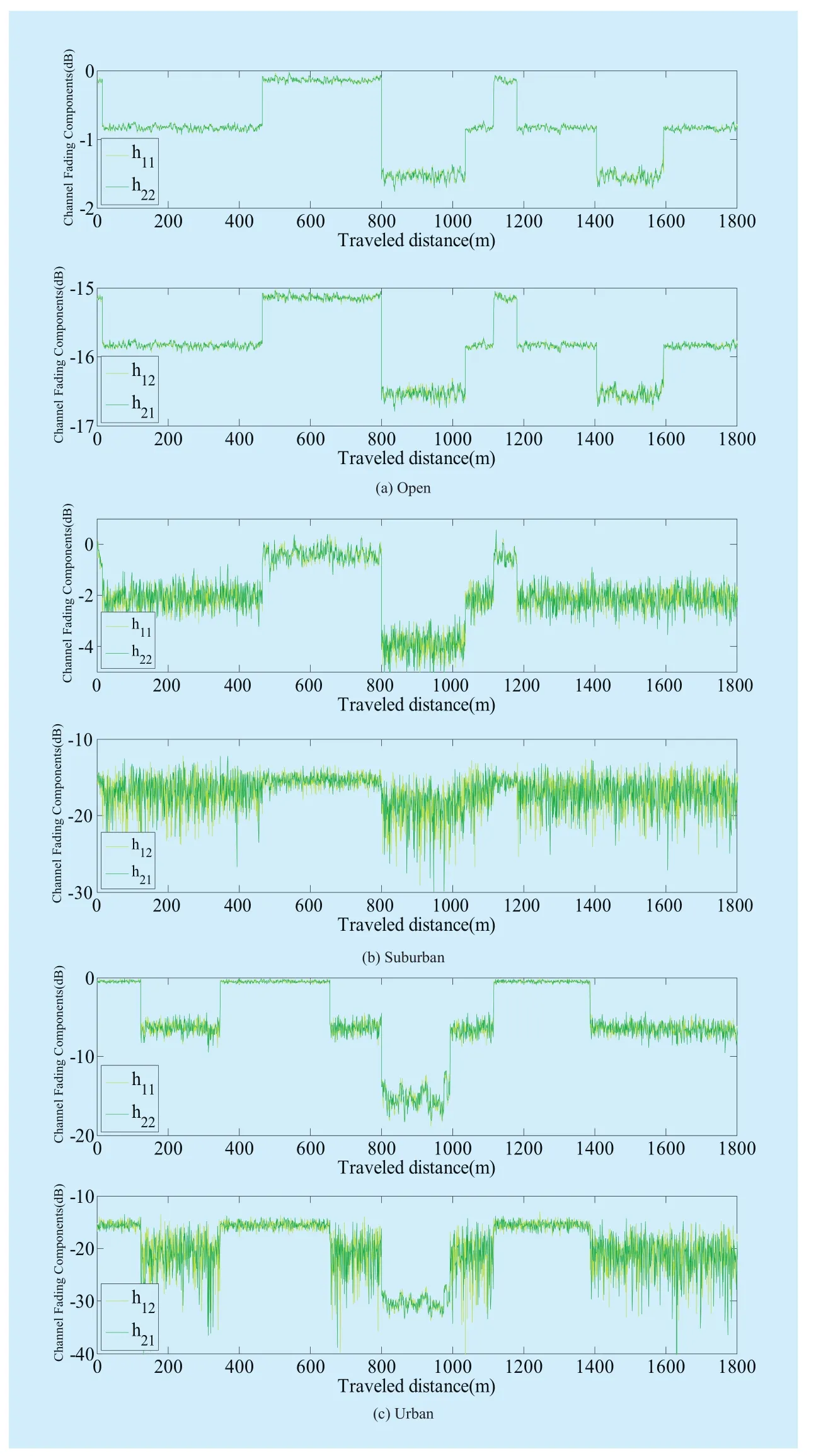
Fig. 4 Time series generated for 2×2 MIMO HAP channel

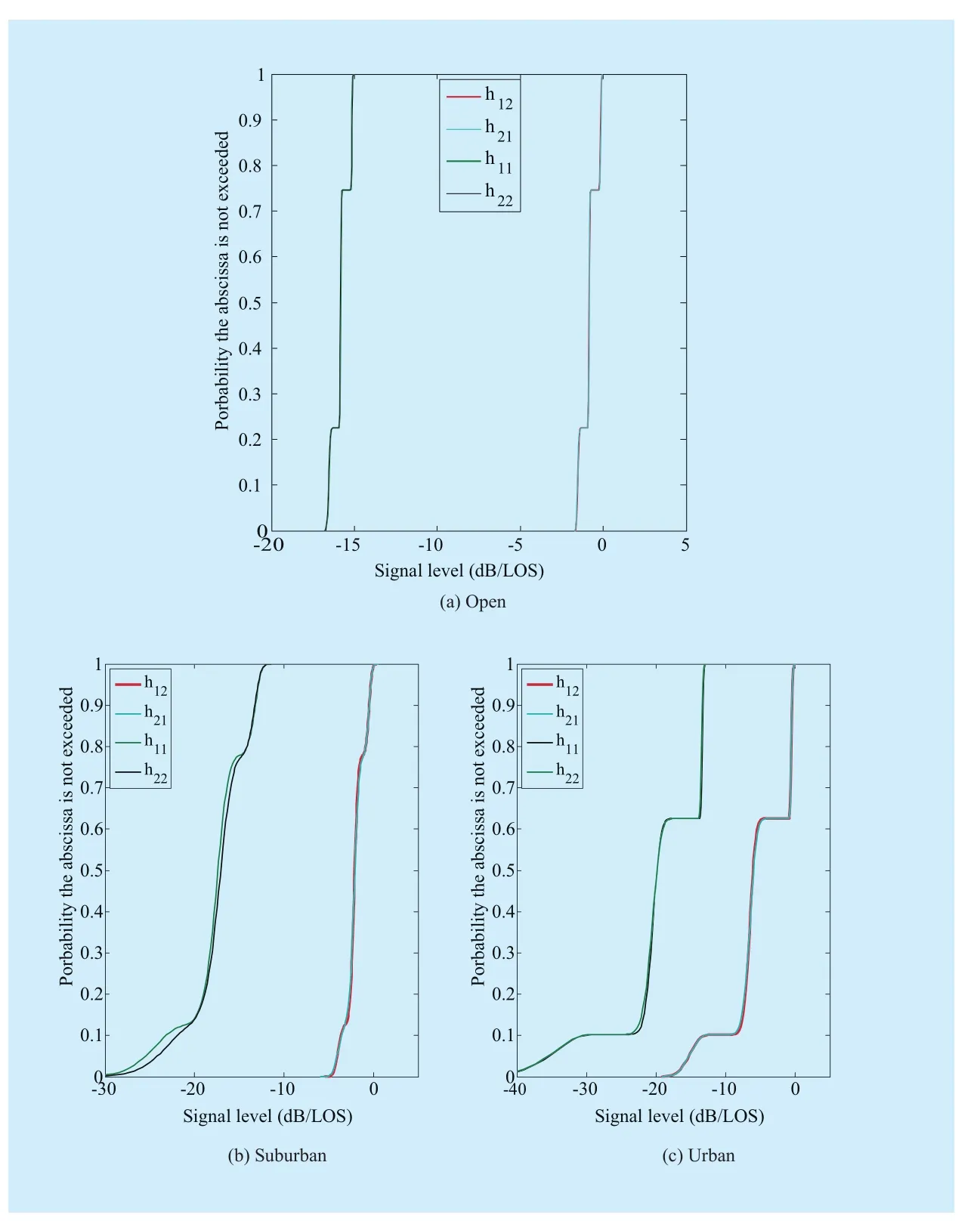
Fig. 5 Cumulative distribution plots of the receiving level for 2×2 MIMO HAP channel

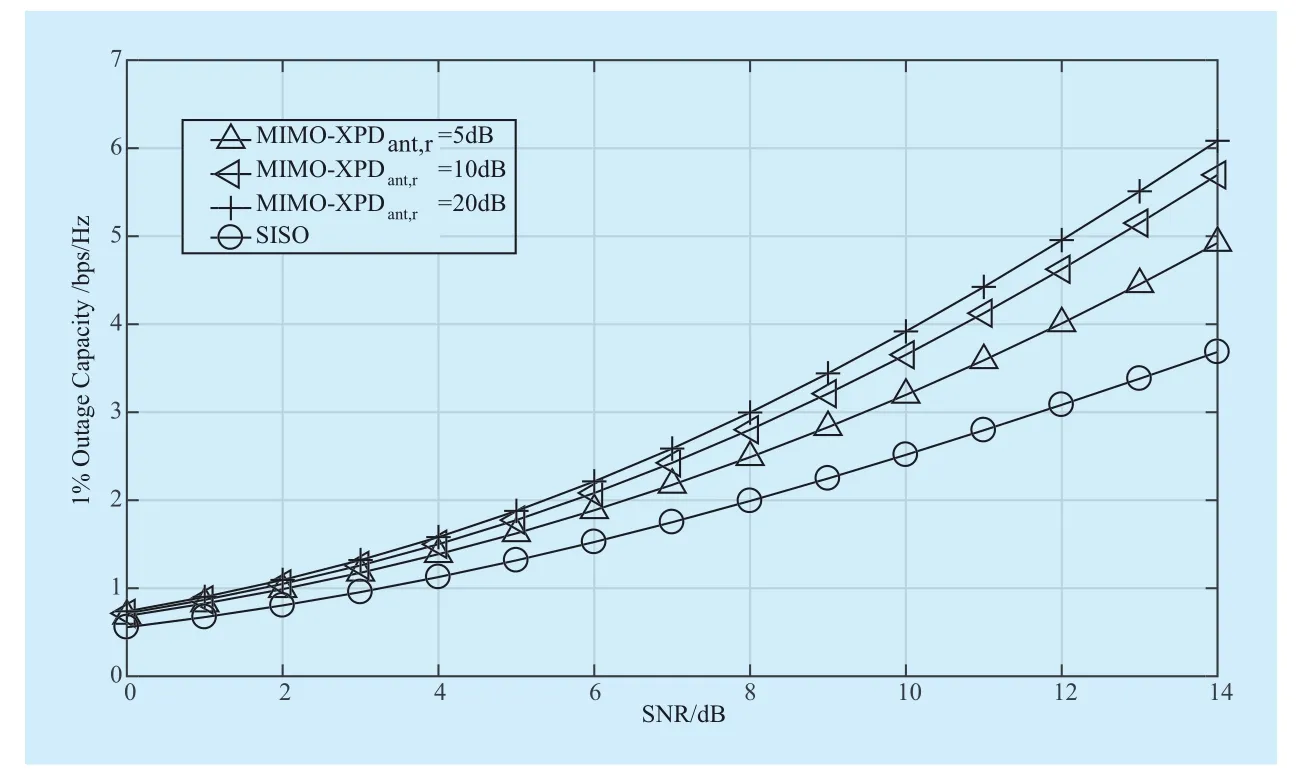
Fig. 6 Simulated results for 1% outage capacity of 2×2 MIMO HAP channel with the change of XPDant,r (Open environment, θ=40°)

Based on the consolidated statistical channel model presented above, a snapshot of the time series generated for a high speed train moving at 300 km/h in an open rural, suburban and urban environment is presented in Fig. 4. And cumulative distribution of the receiving level under the above three states is shown in Fig.5. From the figure, it is obvious that the train experiences three different states, and each state can be described by corresponding Loo statistical parameters (α, ψ, MP). As expected,the simulated cross-polar levels hij(i≠j=1,2)are lower than the co-polar hij(i=j=1,2) components. As currently measured data for HAP system is very limited, thus in this paper measured data of Loo model for satellite propagation channel is applied to the simulation of the HAP channel model [23]. The shadowing correlation matrixassumed is in line with [20]. Besides,other simulation parameters of different environments can be obtained from [11].

For the MIMO HAP system with Nttransmit and Mrreceiver antennas. The capacity is given by [24]

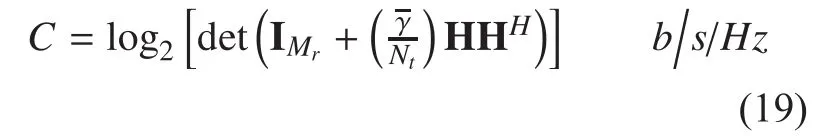
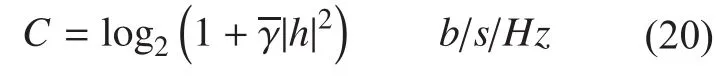
In general, MIMO channels change randomly. Therefore, H is a random matrix,which means that its channel capacity is also randomly time-varying. Thus a statistical notion of the channel capacity, i.e., outage channel capacity, can be applied to analyze the channel capacity. And the outage probability is defined as

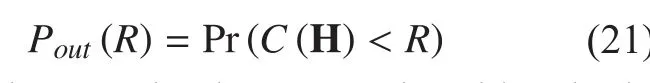
In other words, the system is said to be in outage if the decoding error probability cannot be made arbitrarily small with the transmission rate of R bps/Hz. Then the ε-outage channel capacity is defined as the largest possible data rate such that the outage probability in (21) is less than ε. In other words, it is corresponding to Cεsuch that

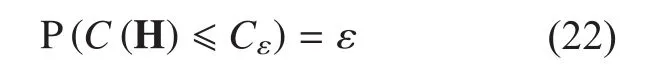
The results of 1% outage capacity obtained from Fig. 6 to Fig. 8 suggest a significant improvement in capacity in a dual polarized 2×2 MIMO HAP system compared with SISO system. In Fig. 6, As XPDant,rincreases, the influence of cross polarization will degrade.And as the diagonalization degree of matrix H in (19) enhances, the outage probability of MIMO channel will increases. That is to say,the outage probability will be reduced and the quality will be enhanced by increasing the XPDant,rof the receiving antenna in the MIMO system. Moreover, Fig. 7 describes that under suburban environment, the change of 2×2 MIMO HAP 1% outage capacities with the varying θ. The outage probability of the signal decreases with large elevation, and the probability for LOS state becomes even higher. Thus, the outage probability for MIMO channel will be improved. Additionally, the elevation of HAP is higher with respect to traditional cellular mobile system, and its channel capacity will be improved greatly.

Fig. 8 indicates that the 1% outage capacity achieved in an urban environment is much lower than that in open and suburban environments. This is because signals are often blocked by high buildings in urban environments, making the outage probability increased. When SNR is 14dB, the SISO 1%outage capacity for the open, suburban and urban environment is 4.24bps/Hz, 2.68bps/Hz and 0.83bps/Hz respectively, whereas for the 2×2 MIMO case, they are 6.90bps/Hz,5.67bps/Hz and 3.08bps/Hz, which increase to 2.66bps/Hz, 2.99bps/Hz and 2.25bps/Hz for each case.

V. CONCLUSION

Considering the stable meteorological conditions and good radio wave transmission characteristics of the stratosphere, a novel notion which utilizes the HAP to carry on multiple-input multiple-output communication is presented. In this paper, a statistical channel model for dual circularly polarized 2×2 MIMO HAP channels is presented. Such model considers both the Doppler shift and temporal correlation, and presents the analysis method of polarization correlation and spatial correlation for each sub-channel. To conquer the problem of lacing measured data of HAP system, the ray tracing approach is applied to the generated digital relief model which covers Xi’an and Zhengzhou in China. The state probability vector and matrix of the state transition probability are generated. And the time series of the receiving signal during the train high-speed operation is obtained through simulation. Besides, useful numerical results on the MIMO HAP channel capacity statistics are also presented illustrating the effect of several critical channel modeling parameters. The results show that, compared with SISO system, MIMO HAP channel outage capacity has been greatly improved under open, suburban and urban environments.

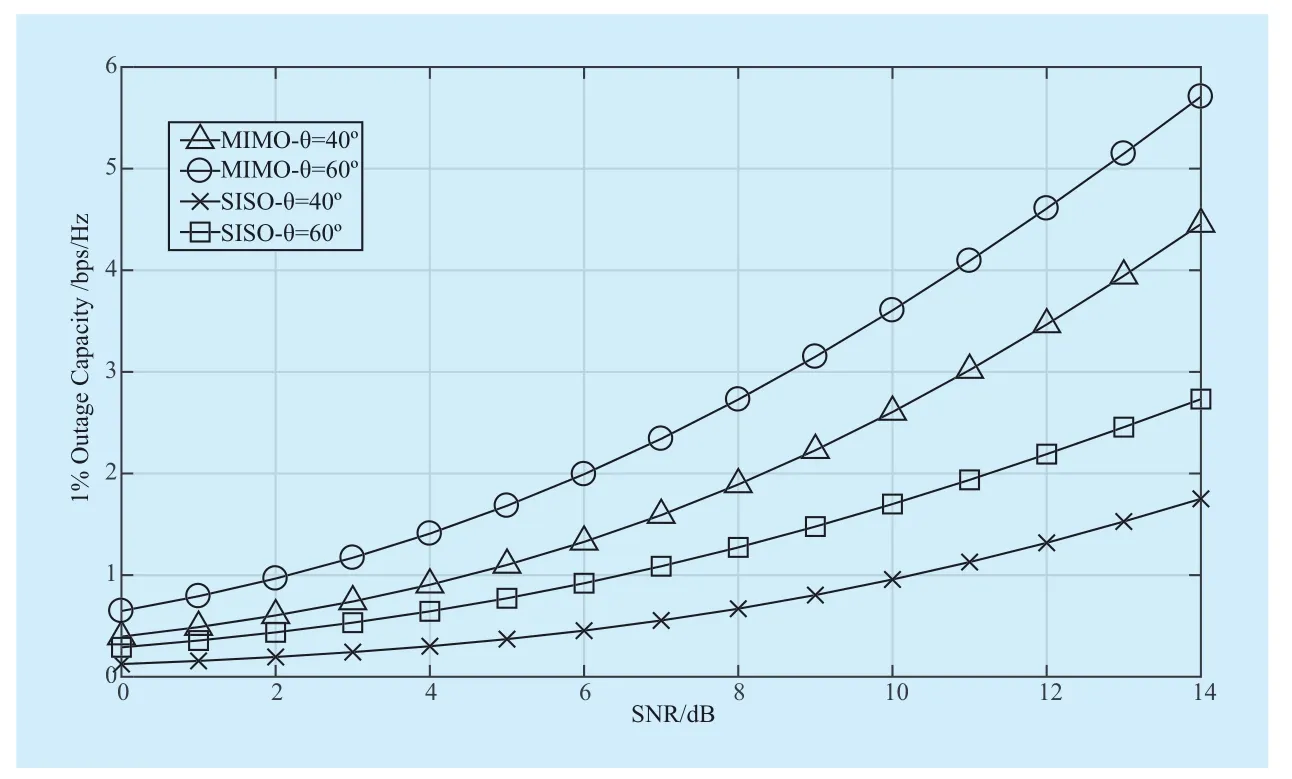
Fig. 7 Simulated results for 1% outage capacity of 2×2 MIMO HAP channel with the change of θ (Suburban environment)

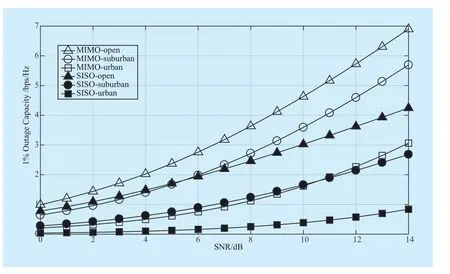
Fig. 8 1% outage capacity for SISO and 2×2 MIMO HAP channel in the open,suburban and urban environments (θ=60°)

ACKNOWLEDGMENT

The paper is sponsored by National Natural Science Foundation of China (No. 91538104,No. 91438205), China Postdoctoral Science Foundation (No. 2011M500664).

[1] Daniel T. Fokum, and Victor S. Frost, “A survey on methods for broadband internet access on trains,”IEEE Communications Surveys & Tutorials, vol. 12, no. 2, pp. 171–185, 2010.

[2] Emanuela Falletti, Massimiliano Laddomada,Marina Mondin, and Fabrizio Sellone, “Integrated services from high-altitude platforms: a flexible communication system,”IEEE Communications Magazine, vol. 44, no. 2, pp. 124–133,Feb. 2006.

[3] D. Grace, N. E. Daly, T. C. Tozer, A. G. Burr and D.A. J. Pearce, “Providing multimedia communications services from high altitude platforms,”Int.J. Satell. Commun., vol. 19, pp. 559–580, 2001.

[4] Cianca, E., Prasad, R., De Sanctis, M., De Luise, A., Antonini, M., Teotino, D. and Ruggieri,M, “Integrated Satellite-HAP Systems,”IEEE Communications Magazine, vol. 43, no. 12, pp.supl.33-supl.39, Dec. 2005.

[5] George P. White, and Yuriy V. Zakharov, “Data communications to trains from high-altitude platforms,”IEEE Transactions on Vehicular Technology, vol. 56, no. 4, pp. 2253–2266, July 2007.

[6] T. Celcer, G. Kandus, T. Javornik, M. Mohorcic, S.Plevel, “Evaluation of diversity gain and system capacity increase in a multiple HAP system,”Proc. Int. Workshop on Satellite and Space Communications, Madrid, Sept. 2006, pp. 114–118.

[7] David Grace, Myles H. Capstick, Mihael Mohorcic, Joachim Horwath, Marco Bobbio Pallavicini and Michael Fitch, “Integrating Users into the Wider Broadband Network via High Altitude Platforms,”IEEE Wireless Communications, vol.12, no. 5, pp. 98–105, Oct. 2005.

[8] S. Plevel, T. Javornik, M. Mohorčič, G. Kandus,“Empirical propagation channel model for high altitude platform communication systems,”23rd AIAA International Communications Satellite Systems Conference, Rome, Sept. 2005, pp.187–194.

[9] J.L. Cuevas-Ruiz and J.A. Delago-Penin, “Channel modeling and simulation in HAPS systems,”Proceedings of European Wireless 2004, Barcelona, Feb. 2004, pp. 24–27.

[10] Pantelis-Daniel Arapoglou, Konstantinos Liolis,Massimo Bertinelli, Athanasios Panagopoulos,Panayotis Cottis, and Riccardo De Gaudenzi,“MIMO over satellite: a review,”IEEE Communications Surveys & Tutorials, vol. 13, no. 1, pp.27–51, 2011.

[11] Konstantinos P. Liolis, Jesús Gómez-Vilardebó,Enrico Casini, and Ana I. Pérez-Neira, “Statistical modeling of dual-polarized MIMO land mobile satellite channels,”IEEE Transactions on Communications, vol. 58, no. 11, pp. 3077–3083,Nov. 2010.

[12] Ana I. Pérez-Neira, Christian Ibars, Jordi Serra,Aitor del Coso, Jesús Gómez-Vilardebó, Màrius Caus and Konstantinos P. Liolis, “MIMO Channel Modeling and Transmission Techniques for Multi-Satellite and Hybrid Satellite-Terrestrial Mobile Networks,”Physical Communication, vol.4, no. 2, pp. 127-139, 2011.

[13] Perez-Neira A, Ibars C, Serra J, del Coso A,Gomez J and Caus M, “MIMO applicability to satellite networks,” in10th Workshop on Signal Processing for Space Communications, SPSC 2008 October 2008.

[14] Javornik T., Mohorcic M., Svigelj A., Ozimek I.,Kandus G., “Adaptive coding and modulation for mobile wireless access via high altitude platforms,”Wirel. Pers. Commun., vol. 32, pp.301–317, 2005.

[15] T. Celcer, T. Javornik, M. Mohorcic, G. Kandus,“Virtual multiple input multiple output in multiple high-altitude platform constellations,”IET Commun., vol. 3, Iss. 11, pp. 1704–1715, 2009.

[16] C. Loo, “A statistical model for a land mobile satellite link,”IEEE Transactions on Vehicular Technology, vol. 34, no. 3, pp. 122–127, Aug.1985.

[17] Masayuki Oodo, Hiroyuki Tsuji, Ryu Miura, Masaaki Maruyama, Mikio Suzuki, Yuichiro Nishi,and Hisashi Sasamoto, “Experiments on IMT-2000 using unmanned solar powered aircraft at an altitude of 20 km,”IEEE Transactions on Vehicular Technology, vol. 54, no. 4, pp. 1278–1294, July 2005.

[18] R. Prieto-Cerdeira, F. Perez-Fontan, P. Burzigotti,A. Bolea-Alamanac and I. Sanchez-Lago, “Versatile Two-State Land Mobile Satellite Channel Model with First Application to DVB-SH Analysis,”Int. J. Satell. Commun., vol. 28, pp. 291–315,2010.

[19] F. P. Fontan, A. Mayo, D. Marote, R. Prieto-Cerdeira, P. Marino, F. Machado and N. Riera, “Review of generative models for the narrowband land mobile satellite propagation channel,”Int.J. Commun. Syst. Network, vol. 26, pp. 291–316,2008.

[20] Peter R. King and Stavros Stavrou. Capacity Improvement for a Land Mobile Single Satellite MIMO System. IEEE ANTENNAS AND WIRELESS PROPAGATION LETTERS, VOL. 5, 2006, 5, pp:98-100

[21] Claude Oestges, Bruno Clerckx, Maxime Guillaud, and Merouane Debbah, “Dual-Polarized Wireless Communications: From Propagation Models to System Performance Evaluation,”IEEE Transactions on Wireless Communications, vol.7, no. 10, pp. 4019-4031, October 2008.

[22] Pantelis-Daniel Arapoglou, Martin Zamkotsian and Panayotis Cottis, “Dual Polarization MIMO in LMS Broadcasting Systems: Possible Bene fits and Challenges,”Int. J. Commun. Syst. Network,vol. 29, pp. 349–366, 2011.

[23] Fernando Pérez Fontán, Maryan Vázquez-Castro, Cristina Enjamio Cabado, Jorge Pita García,and Erwin Kubista, “Statistical modeling of the LMS channel,”IEEE Transactions on Vehicular Technology, vol. 50, no. 6, pp. 1549–1567, Nov.2001.

[24] J. G. Foschini and J. M. Gans, “On limits of wireless communications in a fading environment when using multiple antennas,”Wireless Pres.Commun., vol. 6, no. 3, pp. 311–335, 1998.