Energy Efficiency Optimization for D2D Communications Based on SCA and GP Method

Xiaozheng Gao, Hangcheng Han, Kai Yang, Jianping An

School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China.

* The corresponding author, email: hanhangcheng@bit.edu.cn

I. INTRODUCTION

The exponential increase of wireless data has led to the emergence of a large number of wireless communication systems and networks[1-4]. Device-to-device (D2D) communications have been expected as one of key components for the LTE-Advanced systems [3-5].In D2D communications, two user equipments(UEs) are allowed to exchange data without base station (BS), which can not only increase the spectral efficiency (SE), but also improve the energy efficiency (EE) [1,4].

Due to the data communication explosion,SE plays an essential role in the design of communication systems [6-9]. In order to improve the network throughput, the underlay mode, where D2D user equipment (DUE) uses non-orthogonal resource blocks (RBs) with cellular user equipment (CUE), is preferred when CUE is closer to the BS than DUEs [6]. As a result, the system must deal with much more severe interference than cellular networks, especially in full-duplex D2D systems [10]. Power control is an effective method to cope with the interference and guarantee the quality of service (QoS) of the users [8,9,11,12]. The au-thors of [8] proposed a power control scheme to deal with the interference and maximize the network throughput. In [9], joint mode selection, channel assignment, and power control are adopted to optimize the overall system throughput while guaranteeing the QoS of both D2D and cellular users. In [11], the authors presented two optimal power control schemes to maximize the sum rate and the minimal rate of all D2D links, respectively.

An energy-efficient power control scheme is proposed in the paper for device-to-device (D2D) communications underlaying cellular networks,where multiple D2D pairs reuse the same resource blocks allocated to one cellular user.

Apart from the network throughput, EE has also caught more and more attention due to the increasing power consumption of communication industry and little progress in improving the battery capacity of UEs [13–17]. The authors of [13] proposed a two-tier deployment of D2D communications to minimize the power consumption. In [14], the authors investigated the trade off between EE and SE in D2D underlaying cellular networks. The authors of[15] optimized the minimum weighted EE of D2D links in a single macro-cell, where the RBs can be reused by at most one D2D pair.In [16,17], the authors exploited interference temperature approach to improve EE in D2D underlaying communications and orthogonal frequency division multiple access systems with large-scale BS antennas, respectively.

In addition, multiple D2D pairs sharing the same RBs can further improve the SE and frequency reuse factor [18-20]. In [18], the authors presented the bounds of the maximum network throughput in the scenario where one RB can be used by one CUE and multiple D2D pairs. Based on game theory, the authors of [19] proposed interference coordination strategies in a single-cell network, where there exists interference among D2D pairs due to the fact that RBs are reused by multiple D2D pairs. In [20], the authors investigated a model that multiple D2D pairs could share subchannels with multiple cellular users, and optimized the throughput of D2D pairs while satisfying the data rate requirements of cellular users.

In this paper, we propose an EE-maximization power control scheme in the scenario where the same RBs can be reused by multiple D2D pairs. Compared with [8,9], we take the EE instead of the SE as the objective function.Compared with [15], in which at most only one D2D pair can share the same RBs with one CUE, we consider the scenario of multiple D2D pairs reusing the same RBs allocated to one CUE, which can further improve the SE and frequency reuse factor. We formulate the EE-maximization power control problem as a fractional programming (FP) problem, and then equivalently transform it into a series of parametric subtractive-form problems, which are still non-concave due to the existence of interference. Instead of using interference temperature method [16,17], in which extra constraints are added on the interferences to convert the non-concave problems into concave ones, we adopt successive convex approximation (SCA) and geometric programming (GP)method to obtain the solutions satisfying the Karush-Kuhn-Tucker (KKT) conditions of parametric subtractive-form problems. Extensive simulations are conducted to verify the effectiveness of the proposed scheme, and it is shown that SCA and GP method outperforms interference temperature method.

The rest of the paper is organized as follows. Section II presents the system model.The EE-maximization power control scheme is proposed in Section III. Simulation results are shown in Section IV, and the paper is concluded in Section V.

II. SYSTEM MODEL

In this paper, we consider a single-cell network, where M pairs of DUEs reuse K RBs allocated to one CUE, as illustrated in Fig. 1.Since uplink RBs are preferred for D2D communications [21], we treat the CUE and the BS as a virtual D2D pair, in which the CUE and the BS correspond to the D2D transmitter and D2D receiver, respectively. For the sake of brevity, we denote the virtual D2D pair as the zeroth D2D pair [23].

We consider both large-scale fading and small-scale fading. Thus, the channel vector between the transmitter of the m'-th D2D pair and the receiver of the m-th D2D pair on the k-th RB can be expressed as

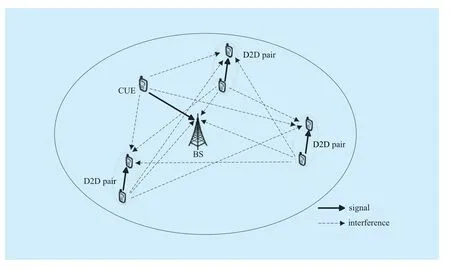
Fig. 1 Single cell scenario with one CUE and multiple D2D pairs

The power consumption of D2D communications is made up with two parts: the transmission power consumption and average circuit power consumption [22]. Therefore,the power consumption of the m-th D2D pair can be denoted as

And the EE of the network, which is defined as the ratio of the total throughput over the total power consumption [22], is expressed as

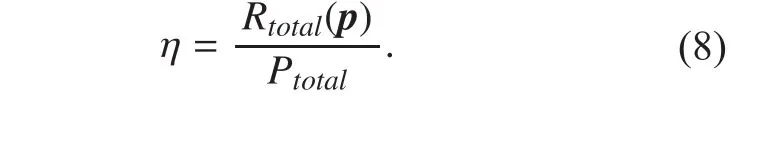
III. EE-MAXIMIZATION POWER CONTROL SCHEME

In this section, we will investigate the EE-maximization power control scheme for D2D communications. Taking the minimum data rate requirement and the maximum allowed transmit power into consideration, the EE-maximization problem can be formulated as

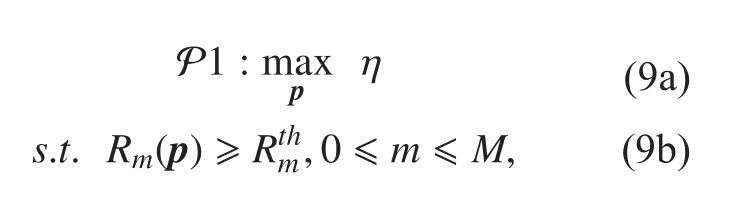
In the following, we will develop a twoloop iterative algorithm to solve the original EE-maximization problemIn the outer

Algorithm 1 Outer Loop of Deriving based on Dinkelbach Method

Algorithm 1 Outer Loop of Deriving based on Dinkelbach Method

1. Initialize tolerance, iteration number , and .2. repeat 3.4. Solve with to obtain the optimal solution .5.with .6. until .

Algorithm 2 Inner Loop of Solvingwith Givenbased on SCA and GP Method

Algorithm 2 Inner Loop of Solvingwith Givenbased on SCA and GP Method

1. Set tolerance , iteration number , and initial values .2. repeat 3.4. Update the parameters , based on (16a) and (16b),respectively.5. Solve and with using interior-point method.6. until to obtain the solution.

3.1 Outer loop

3.2 Inner loop

For the sake of brevity, we introduce auxiliary variablesandandis transformed as:

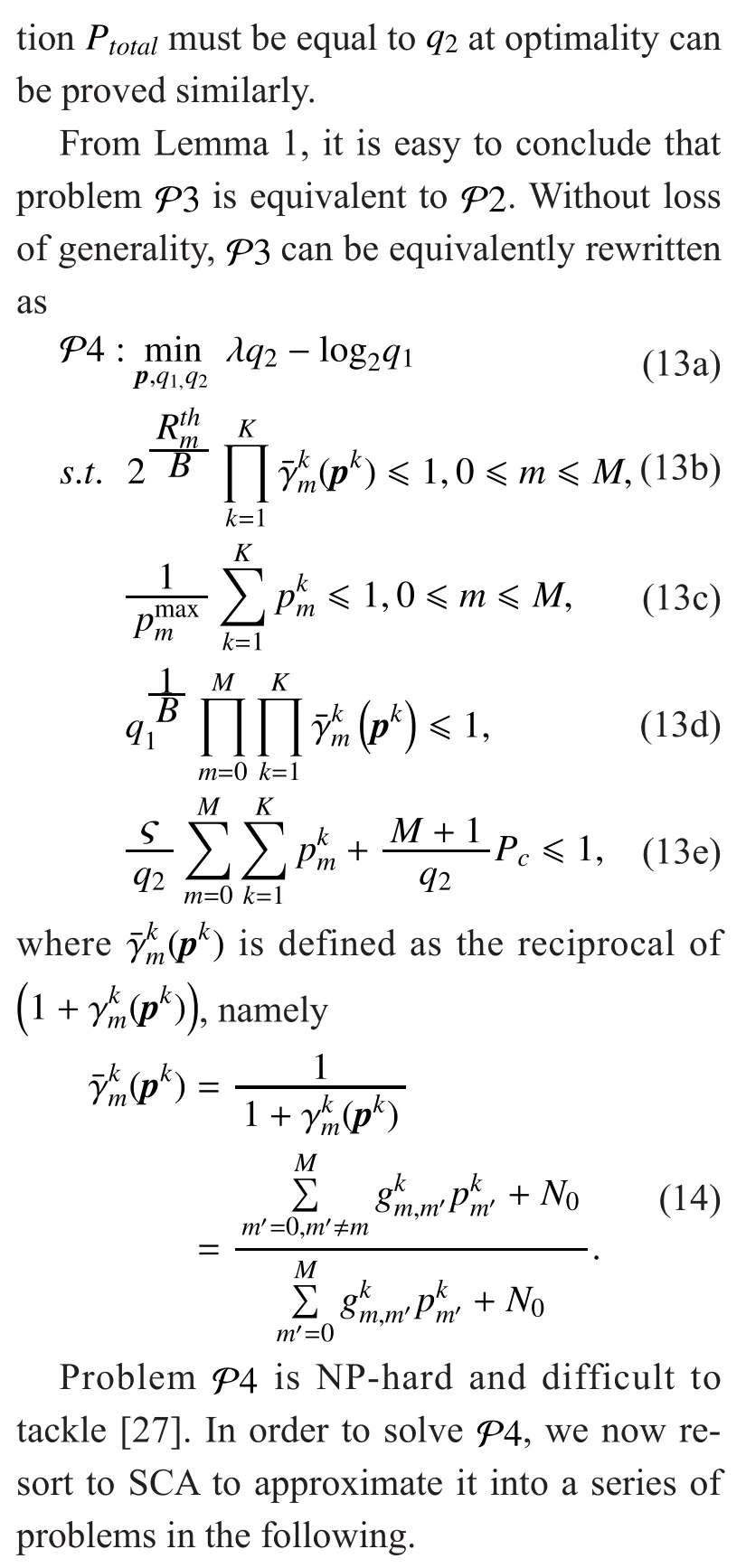
Based on Jensen’s inequality, namely, the arithmetic mean is greater than or equal to the geometric mean for any set of positives [26],we have

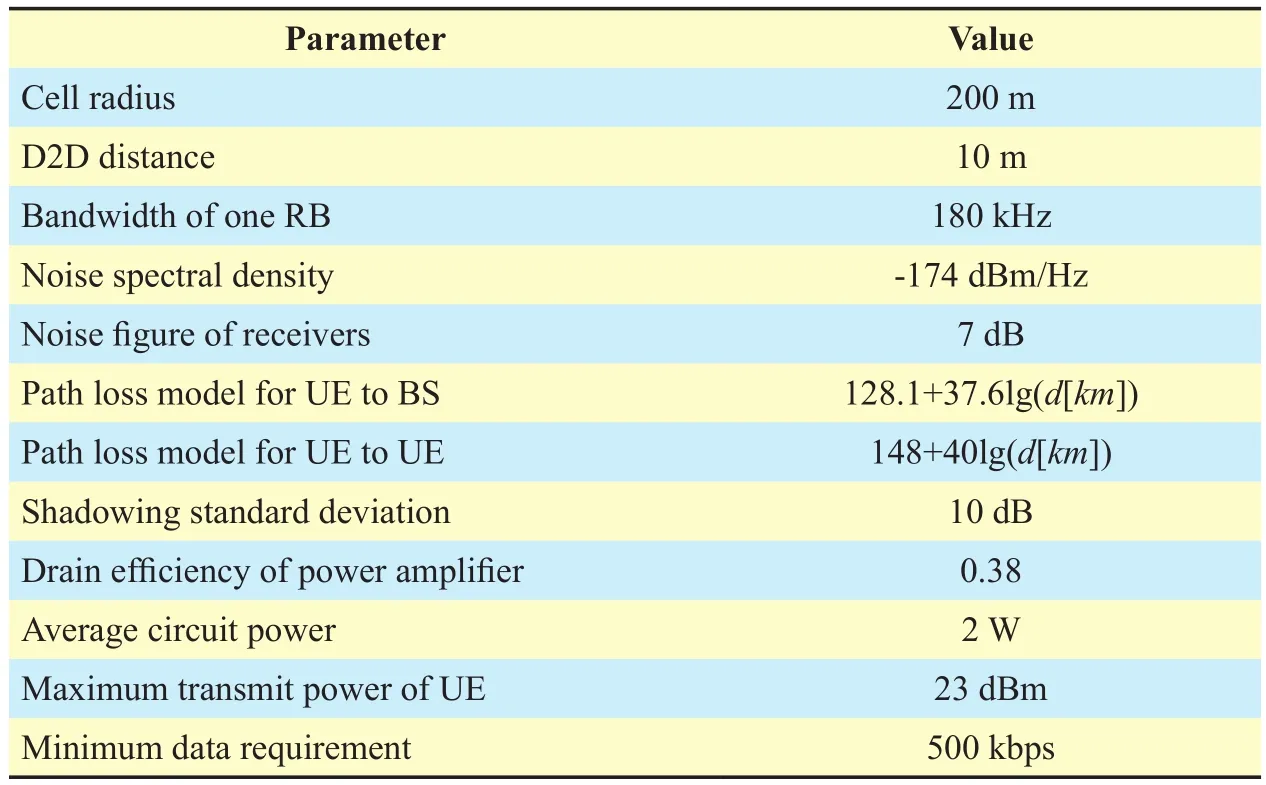
Table I Simulation parameters

Table II The value of versus iteration times in Algorithm 1

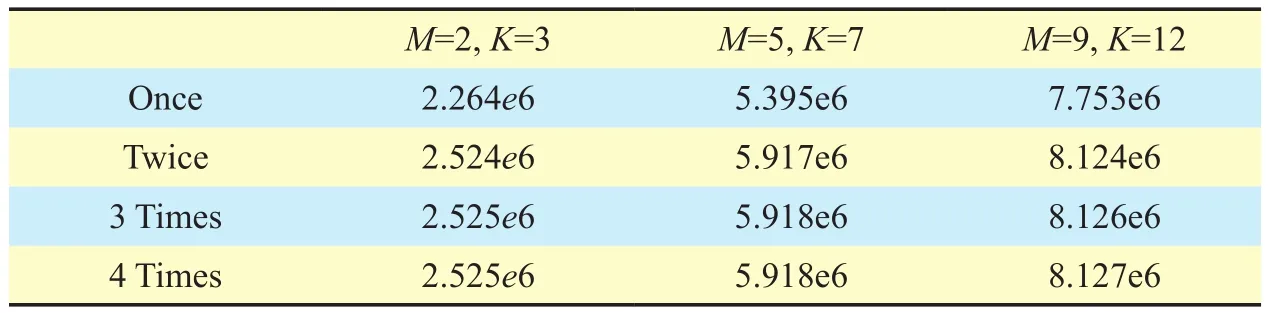
Table II The value of versus iteration times in Algorithm 1

M=2, K=3 M=5, K=7 M=9, K=12 Once 2.264e6 5.395e6 7.753e6 Twice 2.524e6 5.917e6 8.124e6 3 Times 2.525e6 5.918e6 8.126e6 4 Times 2.525e6 5.918e6 8.127e6

Table III The value ofversus iteration times in Algorithm 2

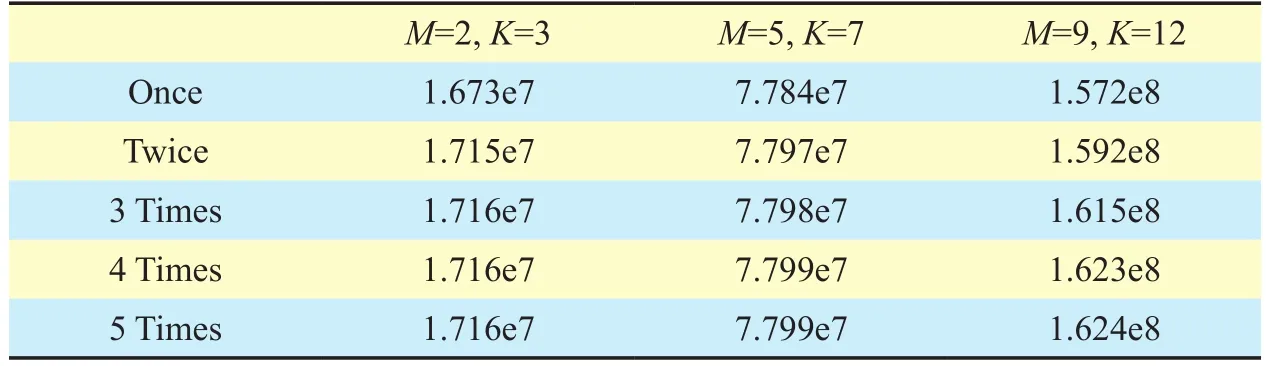
Table III The value ofversus iteration times in Algorithm 2

M=2, K=3 M=5, K=7 M=9, K=12 Once 1.673e7 7.784e7 1.572e8 Twice 1.715e7 7.797e7 1.592e8 3 Times 1.716e7 7.798e7 1.615e8 4 Times 1.716e7 7.799e7 1.623e8 5 Times 1.716e7 7.799e7 1.624e8

IV. SIMULATION RESULTS

In this section, we consider a single-cell network, in which the BS is located in the center and UEs are uniformly distributed. The default parameters of simulations are summarized in Table I. Here, we first illustrate the convergence of the algorithms, and then present the system performance versus some parameters including D2D pair number, RB number, D2D link distance, and maximum allowed transmit power.

The convergence behaviors of Algorithms 1 and 2 are examined in Tables II and III, respectively. Table II illustrates the convergence speeds of the outer loops of three snapshots.From Table II, we find that the outer loop converges to the optimal solution within 3 or 4 times. The inner loops withof three snapshots are presented in Table III, indicating that the inner loop also converges very fast.From Tables II and III, we can conclude that the iteration times do not increase significantly with the increase of D2D pairs and RBs.

The impacts of D2D pair number M on the average EE and average network throughput are shown in Figs. 2 and 3, respectively. On the one hand, it is obvious that the average EE decreases with M due to the fact that increasing D2D pair would aggravate the interference among D2D pairs. On the other hand, we find that the average network throughput increases with M. The larger the M, the higher the reuse factor, and hence the larger the network throughput. We also observe that the average EE and the average network throughput are improved with the increase of RBs due to increased frequency diversity.

Fig. 4 shows the impact of D2D link distance on the average EE. We find that the average EE decreases significantly with the increase of D2D link distance. The larger the D2D link distance, the higher the transmit power is needed to compensate for the pathloss, and hence the lower the EE. It is shown that the average EE decreases more than 70% in all scenarios with the increase of D2D link distance d from 5 m to 30 m. In addition, we compared the average EE of our proposed approach with that of interference temperature method, in which extra constraints are added on the interferences to transform the non-concave problems into concave ones [16, 17]. It is noticeable that the average EE of our proposed approach outperforms that of interference temperature method due to the fact that the latter method cannot converge to the KKT solution of

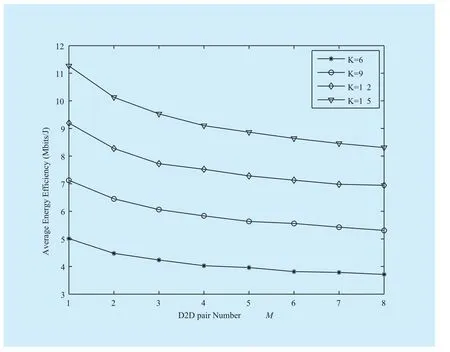
F ig. 2 Average EE versus D2D pair number

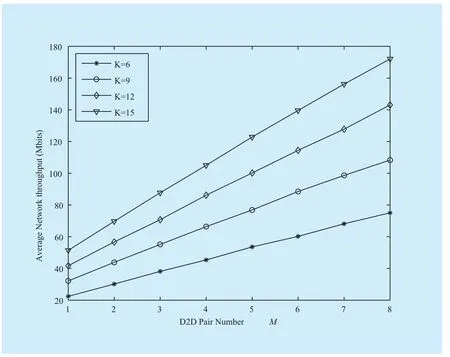
Fi g. 3 Average network throughput versus D2D pair number

V. CONCLUSION

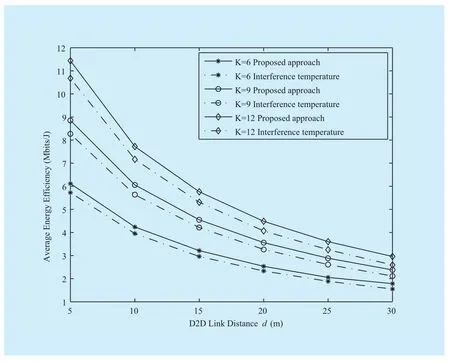
Fig. 4 Average EE versus D2D link distance (M = 3)

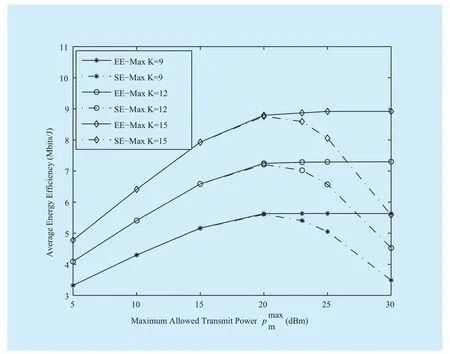
Fig. 5 Average EE versus maximum allowed transmit power (M = 5)

In this paper, we have investigated the EE-maximization power control scheme for D2D communications underlaying cellular networks, where multiple D2D pairs reuse the same RBs allocated to one CUE. We formulated the EE-maximizaiton problem as a non-concave FP problem, and then developed a two-loop iterative algorithm, in which the outer loop is based on Dinkelbach method and the inner loop is based on SCA and GP method, to address the problem. Simulation results have demonstrated the effectiveness of the proposed scheme, and also revealed the basic relationship between different parameters and system performance, which could provide useful guidance to energy-efficient power control in D2D communications.

ACKNOWLEDGEMENTS

This work was partly supported by National Natural Science Foundation of China (No.61501028) and Beijing Institute of Technology Research Fund Program for Young Scholars.

[1] K. Doppler, M. Rinne, C. Wijting,et al., “Device-to-device communication as an underlay to LTE-advanced networks,”IEEE Commun.Mag., vol. 47, no. 12, pp. 42-49, Dec. 2009.

[2] Z. Zhang, K. Long, J. Wang,et al., “On swarm intelligence inspired self-organized networking:its bionic mechanisms, designing principles and optimization approaches,”IEEE Commun. Surv.Tut., vol. 16, no. 1, pp. 513-537, 1st Quart. 2014.

[3] G. Fodor, E. Dahlman, G. Mildh,et al., “Design aspects of network assisted device-to-device communications,”IEEE Commun. Mag., vol. 50,no. 3, pp. 170-177, Mar. 2012.

[4] S. Y. Lien, C. C. Chien, F. M. Tseng,et al., “3GPP device-to-device communications for beyond 4G cellular networks,”IEEE Commun. Mag., vol.54, no. 3, pp. 29-35, Mar. 2016.

[5] 3GPP TR 23.703 V12.0.0, “Study on architecture enhancements to support proximity-based services,” Mar. 2014.

[6] Z. Liu, T. Peng, S. Xiang,et al., “Mode selection for device-to-device (D2D) communication under LTE-advanced networks,” inProc. IEEE ICC,pp. 5563-5567, Jun. 2012.

[7] Z. Zhang, K. Long and J. Wang, “Self-organization paradigms and optimization approaches for cognitive radio technologies: a survey,”IEEE Wireless Commun., vol. 20, no. 2, pp. 36-42, Apr.2013.

[8] C. H. Yu, O. Tirkkonen, K. Doppler,et al., “Power optimization of device-to-device communication underlaying cellular communication,” inProc. IEEE ICC, pp. 1-5, Jun. 2009.

[9] G. Yu, L. Xu, D. Feng,et al., “Joint mode selection and resource allocation for device-to-device communications,”IEEE Trans. Commun., vol. 62,no. 11, pp. 3814-3824, Nov. 2014.

[10] Z. Zhang, K. Long, A. V. Vasilakos,et al., “Full-duplex wireless communications: challenges, solutions and future research directions,”Proceedings of the IEEE, vol. 104, no. 7, pp. 1369-1409,Jul. 2016.

[11] Y. Ren, F. Liu, Z. Liu,et al., “Power control in D2D-based vehicular communication networks,”IEEE Trans. Veh. Technol., vol. 64, no. 12, pp.5547-5562, Dec. 2015.

[12] Z. Zhang, X. Chai, K. Long,et al., “Full-duplex techniques for 5G networks: self-interference cancellation, protocol design and relay selection,”IEEE Commun. Mag., vol. 53, no. 5, pp.128-137, May 2015.

[13] Y. A. Sambo, M. Z. Shakir, K. A. Qaraqe,et al.,“Energy efficiency improvements in HetNets by exploiting device-to-device communications,”inProc. European Signal Processing Conference(EUSIPCO), pp. 151–155, Sep. 2014.

[14] Z. Zhou, M. Dong, K. Ota,et al., “Energy efficiency and spectral efficiency tradeoff in device-to-device (D2D) communications,”IEEE Wirel. Commun. Lett., vol. 3, no. 5, pp. 485-488,Oct. 2014.

[15] T. D. Hoang, L. B. Le and T. Le-Ngoc, “Energy-efficient resource allocation for D2D communications in cellular networks,”IEEE Trans. Veh. Tech-nol., vol. 65, no. 9, pp. 6972-6986, Sep. 2016.

[16] K. Yang, S. Martin, C. Xing,et al., ”Energy-effi-cient power control for device-to-device communications,”IEEE J. Sel. Areas Commun., vol.34, no. 12, pp. 3208-3220, Dec. 2016.

[17] D. W. K. Ng, E. S. Lo, and R. Schober, “Energy-efficient resource allocation in OFDMA systems with large numbers of base station antennas,”IEEE Trans. Wireless Commun., vol. 11, no. 9, pp.3292-3304, Sep. 2012.

[18] M. Ni, L. Zheng, F. Tong,et al., “A geometrical-based throughput bound analysis for device-to-device communications in cellular networks,”IEEE J. Sel. Areas Commun., vol. 33, no.1, pp. 100-110, Jan. 2015.

[19] R. Yin, G. Yu, H. Zhang,et al., “Pricing-based interference coordination for D2D communications in cellular networks,”IEEE Trans. Wireless Commun., vol. 14, no. 3, pp. 1519-1532, Mar.2015.

[20] W. Zhao and S. Wang, “Resource sharing scheme for device-to-device communication underlaying cellular networks,”IEEE Trans. Commun., vol. 63, no. 12, pp. 4838-4848, Dec. 2015.

[21] D. Feng, L. Lu, Y. Yuan-Wu,et al., “Device-to-device communications underlaying cellular networks,”IEEE Trans. Commun., vol. 61, no. 8, pp.3541-3551, Aug. 2013.

[22] C. Xiong, G. Y. Li, S. Zhang,et al., “Energy-effi-cient resource allocation in OFDMA networks,”IEEE Trans. Commun., vol. 60, no. 12, pp. 3767-3778, Dec. 2012.

[23] K. Yang, J. Wu, X. Gao,et al., “Energy-efficient power control for device-to-device communications with max-min fairness,” inProc. IEEE Veh.Technol. Conf., pp. 1-6, Sep. 2016.

[24] W. Dinkelbach, “On nonlinear fractional programming,”Management Science, vol. 13, no. 7,pp. 492-498, Mar. 1967.

[25] B. R. Marks and G. P. Wright, “A general inner approximation algorithm for non-convex mathematical programs,”Oper. Res., vol. 26, no. 4,pp. 681–683, Jul. 1978.

[26] S. Boyd and L. Vandenberghe,Convex Optimization. Cambridge University Press, 2004.

[27] S. Boyd, S. J. Kim, L. Vandenberghe,et al., “A tutorial on geometric programming,”Optim. Eng.,vol. 8, no. 1, pp. 67-127, Mar. 2007.