带肋圆形截面钢桥墩的延性性能预测
刘乃藩, 高圣彬
(上海交通大学 船舶海洋与建筑工程学院, 上海 200240)
带肋圆形截面钢桥墩的延性性能预测
刘乃藩, 高圣彬
(上海交通大学 船舶海洋与建筑工程学院, 上海 200240)
为了解带肋圆形截面钢桥墩在承受轴向压力和水平往复荷载作用下的无量纲化极限承载力和延性性能,通过与既有试验结果对比,确定所采用的有限元建模方法和修正双曲面钢材本构模型的准确性.针对能有效提高圆形截面钢桥墩延性性能的八根肋形式的钢桥墩模型,研究截面正则径厚比、钢桥墩正则长细比、加劲肋正则长细比和轴压比等参数对钢桥墩延性性能和无量纲化极限承载力的影响,并基于参数化分析结果,拟合预测该类钢桥墩的延性性能和无量纲化极限承载力的计算公式.研究结果表明:修正双曲面本构模型能够较准确预测钢桥墩的力学性能,且随着正则径厚比、钢桥墩正则长细比、加劲肋正则长细比和轴压比的减小,桥墩的无量纲化极限承载力和延性性能得到显著提高.
桥梁工程;钢桥墩;修正双曲面模型;无量纲化极限承载力;延性性能
钢桥墩在遭受罕遇地震时将承受巨大的往复作用,其抵抗能力取决于它的极限承载力和延性性能.由于影响钢桥墩滞回性能的因素较多,若是通过伪静力试验得到其荷载-位移滞回曲线,成本消耗巨大.采用合适的建模方法和本构模型,借助计算机超强的计算能力进行数值模拟是可行而高效的方式.
国内外很多学者针对钢桥墩在水平往复荷载作用下的极限承载力和延性性能进行了很多试验和理论研究.如文献[1]研究了轴压比、长细比、正则径厚比等参数对圆形无肋截面钢桥墩延性性能的影响,并拟合了预测其无量纲化极限承载力和延性比的计算公式. 文献[2-3]研究了压弯荷载作用下无加劲肋和有加劲肋的方形截面短柱的延性性能,在此基础上提出了估算短柱延性性能的计算公式,并提出采用梁-柱单元估算长柱延性比的简化计算方法.文献[4]研究了加劲肋数量、肋长细比、截面正则径厚比等对圆形截面钢桥墩的延性性能影响,发现该类钢桥墩内设8根加劲肋的形式对其延性性能的提高最为明显.文献[5-7]研究了内置十字形钢板补强与外置钢管补强的圆形截面钢桥墩的抗震性能,发现内置钢板和外置钢管改变了钢桥墩的局部失稳模态,并且其延性随着钢桥墩的长细比和径厚比的增大而降低.文献[8]研究了内置T型加劲肋时的圆形截面钢桥墩延性性能,发现用钢量的增加并不一定会提高桥墩的延性比.因而,从权衡经济效益和抗震性能的角度,量化研究钢桥墩的延性性能影响参数具有重要意义.而以上研究大多未考虑钢材本构在计算该类钢桥墩时的适用性和准确性,且未在全面考虑影响带肋圆形钢桥墩延性性能的因素基础上提出可行的计算公式. 本文通过ABAQUS有限元软件的UMAT子程序接口,采用自定义的修正双曲面钢材本构模型(2SM),在与既有试验结果对比验证建模方法和钢材本构模型的基础上,对具有不同正则径厚比、钢桥墩正则长细比、加劲肋正则长细比和轴压比的钢桥墩进行非线性弹塑性有限元计算,研究这些参数对钢桥墩无量纲化极限承载力和延性性能的影响规律.最后基于参数化分析结果,提出了预测钢桥墩无量纲化极限承载力和延性性能的计算公式,为此类钢桥墩的抗震设计提供依据.
1 分析方法
1.1 有限元分析模型
通常此类钢桥墩的局部失稳发生在桥墩底部附近,通过试算确定,在底部0.5D(D为钢桥墩直径)的高度范围内采用加密的四节点壳单元(S4R)划分有限元网格.在0.5D到2D的长度范围内也采用S4R单元,但为了提高计算效率,该区域设定为非加密区.其余部分采用B31梁单元,该梁单元为铁木辛柯梁单元,能够考虑横向剪切变形的影响.此外,为考虑壳单元沿厚度方向的塑性发展,在其厚度方向设置5个积分点.由于在加载平面内的纵向加劲肋面外局部失稳变形并不对称,因此该分析需采用整体模型.有限元分析模型如图1所示.
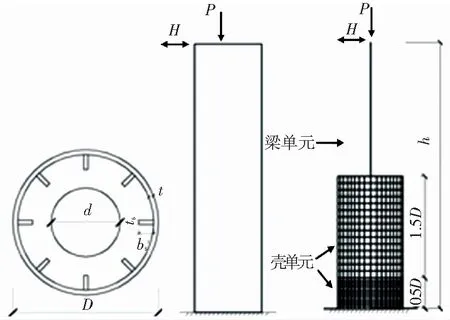
(a)横截面 (b)加载形式 (c)有限元单元划分
1.2 钢材材料属性
文献[9-11]的研究结果表明,在正负往复荷载作用下传统的等向强化、随动强化等本构模型都不能准确预测较厚壁钢桥墩的滞回性能,而修正双曲面模型能够同时较准确地预测薄壁与厚壁钢桥墩的滞回性能.修正双曲面本构模型是基于文献[12]提出的双曲面模型改进发展而来的:1)引入了多轴应力状态下有效塑性应变面的概念;2)定义了屈服面和边界面;3)对形状参数进行了修改;4)提出记忆边界和虚拟边界;5)考虑了边界面移动的影响.本文通过ABAQUS用户子程序接口,使用2SM钢材本构模型子程序进行分析.模型材料常数定义见文献[13],本文采用值见表1,通过与国内常用的Q235B钢材的循环荷载试验结果对比发现,表1中的材料参数同样适用于国内钢材. 试验试件几何属性见表2.1.3 加载方式
首先在柱顶施加恒定竖向荷载,再采用位移加载的方式施加水平往复荷载.水平往复荷载加载制度如图2所示.其中δ为水平位移,δy为水平屈服位移,计算公式为
式中:Hy为偏心受压水平屈服荷载;h为钢桥墩高度;I为横截面惯性矩;My为桥墩截面的屈服弯矩;P为所施加的恒定竖向荷载;Py为全截面屈服轴向荷载.
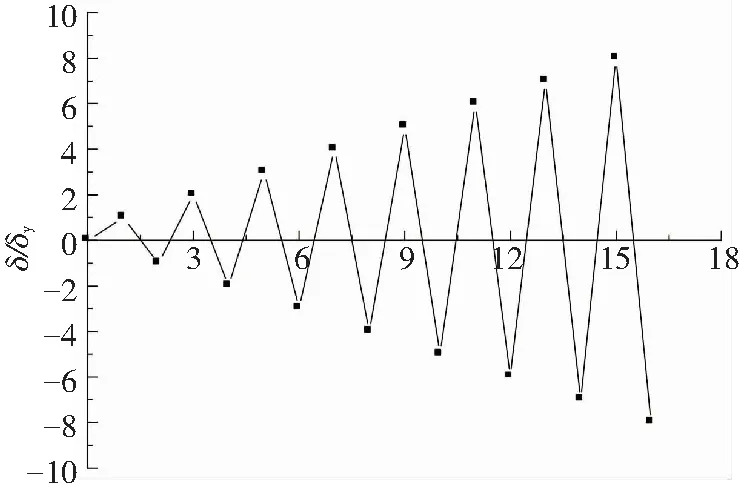
图2 水平往复荷载加载制度

α1α2α3αeMf/EEP0i/Eω·σyk0/σyσu/σyξε2y-0.5052.1714.40.191500-0.370.38.9610-33.081.151.819.8910-4

表2 试验试件几何属性
2 试验对比
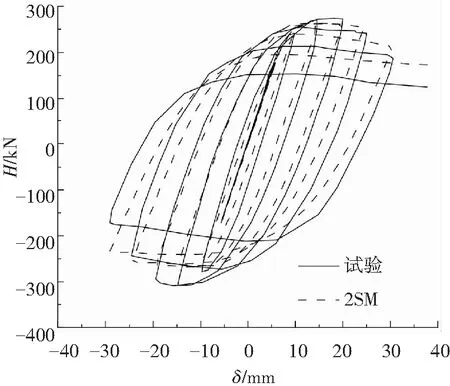
为验证前述的有限元建模方式和2SM本构模型对该类钢桥墩滞回性能预测的准确性,本文对文献[14]中的5号和19号桥墩试件进行模拟计算对比.5号、19号试件分别设置了3根和4根纵向加劲肋,试件高度为1 750 mm.试验中,施加的轴向荷载P为全截面屈服荷载的15%. 由试验和数值模拟得到的柱顶水平荷载-水平位移滞回曲线如图3所示.
(a)No.5

(b)No.19
Fig.3Comparisonoflateralload-lateraldisplacementhystereticcurvesbetweentestsandnumericalresults
可以看出,无论是极限承载力还是滞回环形状,模拟结果与试验结果都吻合较好.通过图4所示的试验和数值模拟的破坏形式对比发现,5号试件的模拟和试验都在受压侧离柱底约140 mm的高度范围内呈现出外突的“象脚型”破坏模态,突出位移约为17 mm.而19号试件的模拟和试验都在受压侧离柱底约150 mm的高度范围内呈现出部分内凹的“钻石型”破坏模态,凹陷位移约为11 mm.数值模拟和试验的破坏形式也保持一致.综上说明,本文所采用的建模方法和2SM本构模型在预测钢桥墩的滞回性能方面具有较高的精度.

图4 试验与数值模拟的破坏模态对比
Fig.4 Comparison of failure modes between tests and numerical results
3 参数影响分析
本文以配置八根加劲肋的圆形截面钢桥墩为分析对象,研究正则径厚比Rt、钢桥墩正则长细比λ、纵向加劲肋正则长细比λs以及轴压比P/Py等主要参数对钢桥墩无量纲化极限承载力和延性性能的影响.试件的几何属性见表3.其中正则径厚比参数Rt定义[15]为
式中:t为钢管壁厚;ν为泊松比;D为桥墩直径.
纵向加劲肋正则长细比λs定义[15]为
式中:Q为相邻纵向加劲肋间板的屈曲强度;γs为纵向加劲肋与其有效宽度范围内的圆管所组成近似T形横截面的回转半径;Rf为钢板的宽厚比;bs为相邻加劲肋间距;b为与加劲肋焊接钢管壁的有效计算宽度[16];lcr为弹性临界波长[4].
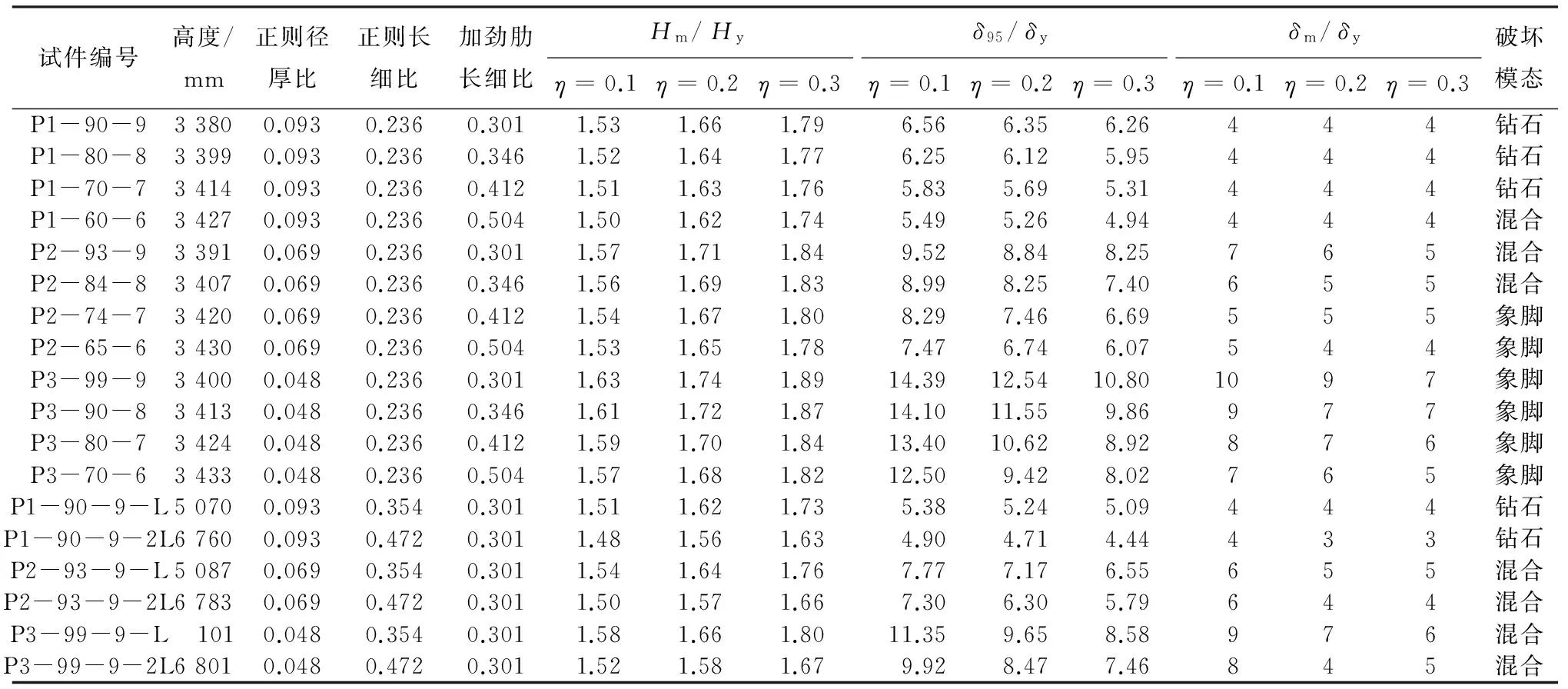
表3 试件几何属性和有限元计算结果
注:试件编号P X-Y-Z中X=1、2、3分别表示钢桥墩的钢管壁厚为9、12.2、17.3mm;Y表示纵向加劲肋从桥墩内壁算起的径向宽度(mm);Z表示纵向加劲肋厚度(mm);L与2L指长细比不同的试件;η指轴压比P/Py; 桥墩直径D取890mm.
柱的正则长细比定义[15]为
式中r为钢桥墩全截面回转半径.
为便于量化分析,本文在得到试件顶端的水平荷载-水平位移滞回曲线后,采用正负方向绝对值平均方式,并将位移和荷载分别除以屈服位移δy、偏心受压水平屈服荷载Hy得到各试件的无量纲化骨架曲线.参数Hm/Hy表示偏心受压水平极限荷载和屈服荷载的比值,该值的大小代表试件的极限承载能力;δm/δy表示最大荷载所对应的位移与屈服位移的比值;δ95/δy表示强度下降到最大荷载值的95%处的位移和屈服位移的比值.由于延性比δm/δy并未充分利用钢材后峰值段的延性性能,因此本文同时将δ95/δy作为延性比指标进行讨论.
3.1 正则径厚比影响
由图5所示的无量纲化水平荷载-水平位移骨架曲线可以看出,正则径厚比参数对于无量纲化极限承载力和延性比的影响明显.随着正则径厚比的增大,试件的无量纲化极限承载力和延性比都显著降低.图5(a)中试件P3-99-9的正则径厚比Rt为0.048,其无量纲化极限承载力处的位移为7δy,而试件P2-93-9(Rt=0.069)无量纲化极限承载力处位移为5δy,试件P1-90-9(Rt=0.093)为4δy,呈下降趋势.同样,三者的无量纲化极限承载力分别为1.89Hy、1.84Hy、1.79Hy,延性比δ95/δy分别为10.8、8.25、6.26,都呈现出随正则径厚比增大而减小的趋势,骨架曲线的下降段变得更加陡峭.说明在地震作用下,试件P3-99-9相较后两者能够吸收更多能量,具有更优的抗震性能.同样的变化规律也可在图5(b)中发现,并且对比图5(c)与图5(d)可知轴压比较大时,该规律更加明显,而加劲肋长细比对其影响较小.因此,在钢桥墩初步设计当中,可以通过降低正则径厚比参数来实现其无量纲化极限承载力和延性性能的提高,且这种提高效果十分显著.
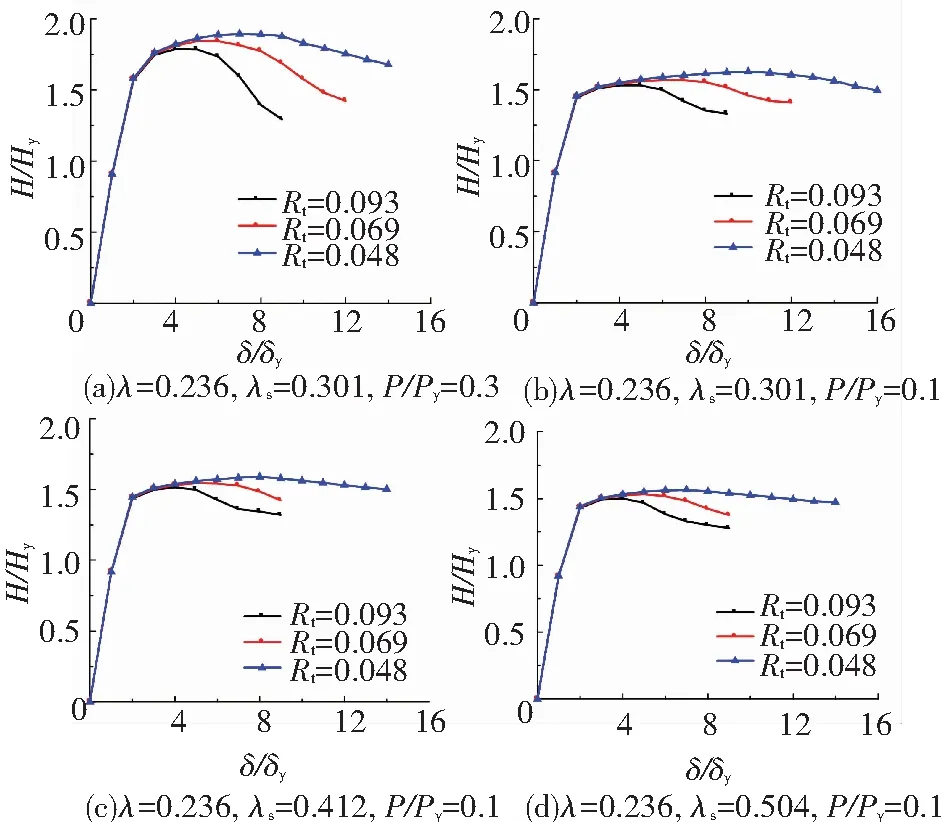
图5 正则径厚比参数影响
3.2 钢桥墩正则长细比影响
钢桥墩正则长细比参数λ对其无量纲化极限承载力和延性性能的影响如图6所示.可以发现,随着钢桥墩正则长细比的增大,其无量纲化极限承载力和延性比都显著降低,这主要是由于长柱的P-Δ效应比短柱更为明显.由图6(a)和图6(b)的比较可以发现,正则长细比所引起的延性值差异对轴压比参数的变化较为敏感.
3.3 加劲肋正则长细比影响
图7为不同加劲肋正则长细比的水平荷载-水平位移骨架曲线.可看出,随着加劲肋正则长细比的减小,钢桥墩的无量纲化极限承载力和延性性能逐步提高,且这种关系在轴压比较大的工况下更为明显.例如与图7(a)相比,图7(b)中的轴压比P/Py由0.1变为0.3,试件P1-90-9(λs=0.301)与P1-60-6(λs=0.504)无量纲化极限承载力和延性比差值显著变大.同时由图7(c)和图7(d)可以看出,加劲肋正则长细比引起的延性差异亦会随着正则径厚比的增大而增加.图8为计算中出现的3种典型破坏模态,通过对比可以发现加劲肋能有效抑制柱脚附近钢板的局部失稳变形.且根据表3模态可知,同一组试件中,加劲肋正则长细比越小,越易出现钻石型破坏,反之则越易出现象脚型破坏.
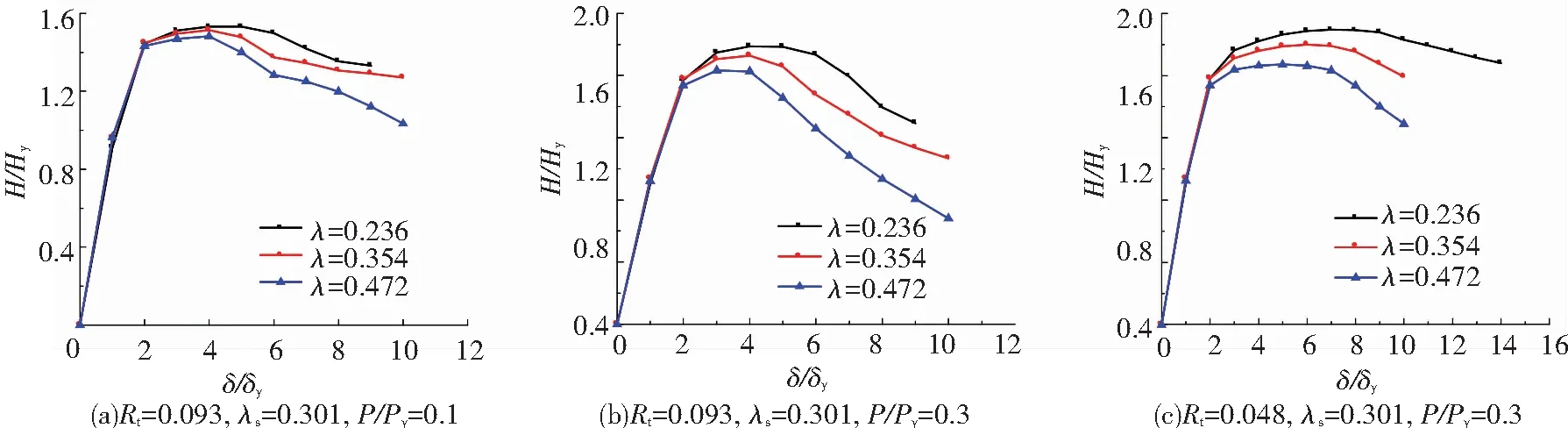
图6 桥墩正则长细比参数影响
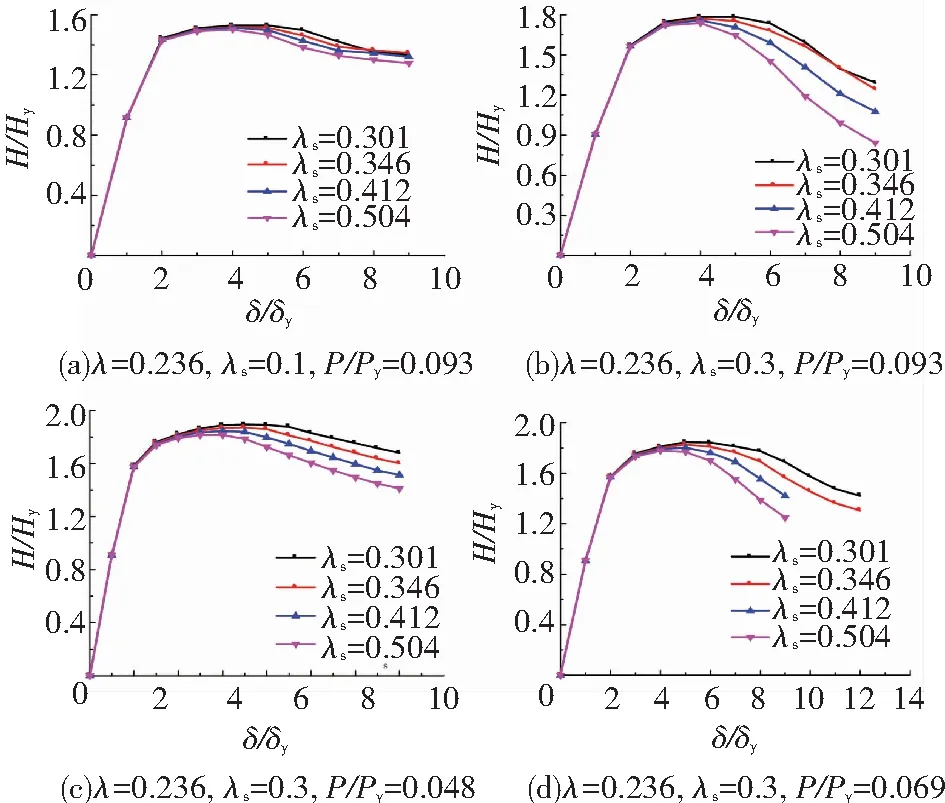
图7 加劲肋正则长细比参数影响

(a)钻石型 (b)混合型 (c)象脚型
3.4 轴压比影响
图9为采用Hy0、δy0进行无量纲化的H/Hy0-δ/δy0骨架曲线.需要说明的是,此处的Hy0、δy0分别指不考虑轴力影响下的钢桥墩水平屈服荷载和水平屈服位移.由图9的骨架曲线比较可知,当其它参数一定时,随着轴压比的增大,无量纲化极限承载力显著下降,延性比也逐渐减小.原因是由于轴力的增加,P-Δ效应也变得更为明显,后峰值段的下降曲线更陡峭,钢桥墩变形与吸能能力变弱.因此,在钢桥墩的抗震设计中,考虑其延性性能对轴压比参数的极度敏感性变得非常重要.在设计该类钢桥墩时,应设定较低的轴压比才能保证其较高的延性比.

(a)λ=0.236,λs=0.301,(b)λ=0.236,λs=0.301,
Rt=0.003Rt=0.069
图9 轴压比参数影响
Fig.9Effectsofnormalizedaxialloadratio
3.5 无量纲化极限承载力和延性比公式拟合
根据表3中的参数化计算结果,本文在考虑纵向加劲肋正则长细比影响的基础上,拟合了带肋圆形截面钢桥墩的无量纲化极限承载力Hm/Hy和延性比δm/δy、δ95/δy的计算公式分别为
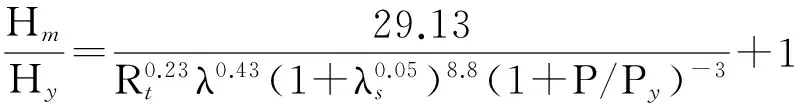
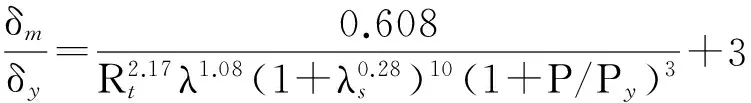

图10为有限元计算结果和拟合公式的对比图,其中S为标准差,M+S和M-S分别表示与拟合曲线相差一个标准差的上限和下限曲线.
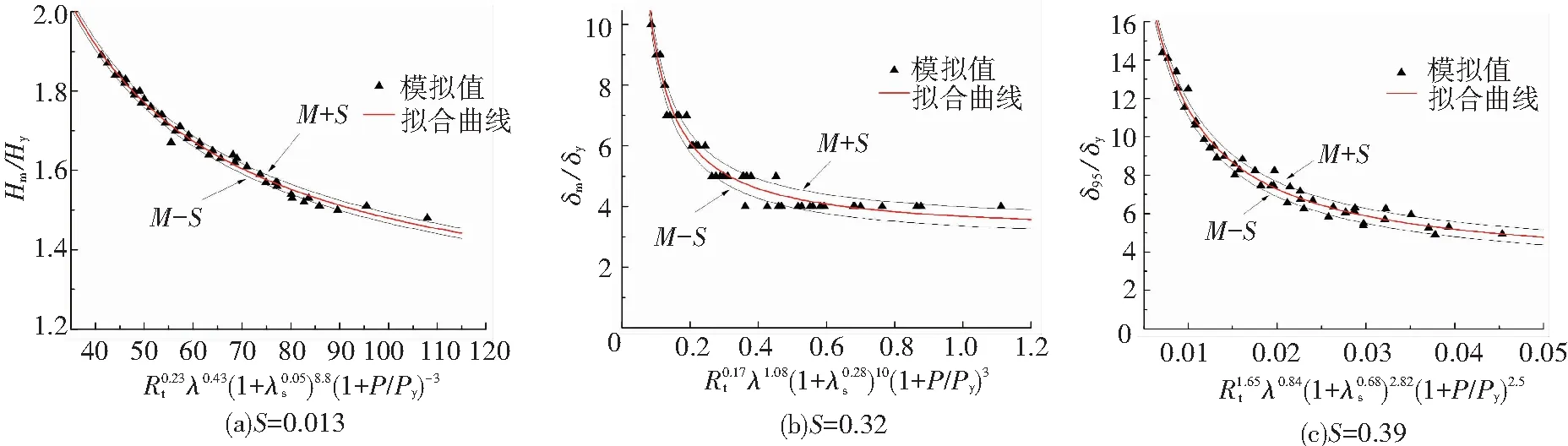
图10 无量纲化极限承载及延性比拟合曲线
4 结 论
1)根据试验值与模拟值的对比结果发现,所采用的建模方法及2SM钢材本构模型能够较好的预测带肋形式的钢桥墩的滞回力学性能.
2)随着钢桥墩正则径厚比、正则长细比、加劲肋正则长细比以及轴压比的减小,桥墩的整体无量纲化承载力和延性性能得到显著提高.
3)根据计算结果拟合的预测该类钢桥墩的无量纲化极限承载力和延性比的计算公式有较好的预测表现,可为该类钢桥墩的抗震初步设计提供理论依据.
[1] GAO Shenbin, USAMI T, GE Hanbin. Ductility evaluation of steel bridge piers with pipe sections[J]. Journal of Engineering Mechanics, 1998, 124(3):260-267.
[2] ZHENG Yi, USAMI T, GE Hanbin. Ductility evaluation procedure for thin-walled steel structures[J]. Journal of Structural Engineering, 2000, 126(11):1312-1319.
[3] 张建东, 葛汉彬, 王春林. 薄壁加劲箱形钢桥墩简化抗震评估方法[J]. 中国公路学报, 2013, 26(1):113-120.
ZHANG Jiandong, GE Hanbin, WANG Chunlin. Simplified seismic evaluation method for steel bridge piers with thin-walled stiffened box sections[J]. China Journal of Highway and Transport, 2013, 26(1):113-120.
[4] 栗岳, 高圣彬. 带肋圆管截面钢桥墩的延性影响因素研究[J]. 钢结构, 2012, 27(7):24-28. DOI: 10.3969/j.issn.1007-9963.2012.07.008.
LI Yue, GAO Shengbin. Researches on the factors affecting the ductility of stiffened steel pipe-setion bridge piers[J]. Steel Construction, 2012, 27(7):24-28. DOI: 10.3969/j.issn.1007-9963.2012.07.008.
[5] 李宁, 王占飞, 隋伟宁. 内置十字钢板补强圆形钢桥墩的抗震性能[J]. 辽宁工程技术大学学报(自然科学版), 2009, 28(2): 243-245.DOI:10.3969/j.issn.1008-0562.2009.02.024.
LI Ning, WANG Zhanfei, SUI Weining. Seismic performance of steel tubular bridge pier with inner cruciform plates[J]. Journal of Liaoning Technical University(Natural Science Edition), 2009, 28(2): 243-245.DOI:10.3969/j.issn.1008-0562.2009.02.024.
[6] 王占飞,孙宝芸,隋伟宁,等.外置钢管补强圆形钢桥墩的抗震性能[J].沈阳建筑大学学报(自然科学版),2009,25(1): 34-38.
WANG Zhanfei , SUN Baoyun, SUI Weining, et al. Study on seismic performance of steel tubular bridge pier with outer pipe[J]. Journal of Shenyang Jianzhu University(Natural Science), 2009, 25(1):34-38.
[7] WANG Zhanfei, TOSHITAKA Y. Ultimate strength and ductility of stiffened steel tubular bridge piers[J].International Journal of Steel Structures, 2011, 11(1):81-90.DOI:10.1007/S13296-011-1007-5
[8] 包龙生, 廖晶, 王占飞. 内置T型钢板补强圆形钢桥墩抗震性能研究[J]. 沈阳建筑大学学报(自然科学版), 2010, 26(4):665-669.
BAO Longsheng, LIAO Jing, WANG Zhanfei. Study on seismic performance of circular steel bridge piers with T-reinforcing rib[J].Journal of Shenyang Jianzhu University(Natural Science), 2010, 26(4):665-669.
[9 ] 高圣彬, 葛汉彬. 交替荷载作用下钢材本构模型的适用范围[J]. 中国公路学报, 2008, 21(6):69-75, 113.
GAO Shengbin, GE Hanbin. Applicable range of steel constitutive models under cyclic load[J].China Journal of Highway and Transport, 2008, 21(6): 69-75, 113.
[10]GANG Shi, MENG Wang, YU Bai,et al. Experimental and modeling study of high-strength structural steel under cyclic loading[J]. Engineering Structures, 2012, 37(7):1-13. DOI:10.1016/j.engstruct.2011.12.018.
[11]王彤, 谢旭, 唐站站, 等. 考虑复杂应变历史的钢材修正双曲面滞回模型[J]. 浙江大学学报(工学版), 2015, 49(7):1305-1312.DOI:10.3785/j.issn.1008-973X.2015.07.015.
WANG Tong, XIE Xu, TANG Zhanzhan, et al. Modified two-surface steel hysteretic model considering complex strain history[J]. Journal of Zhejiang University(Engineering Science), 2015, 49(7):1305-1312.DOI:10.3785/j.issn.1008-973X.2015.07.015.
[12]DAFALIAS Y F,POPOV E P. A model of nonlinear hardening materials for complex loading[J]. Acta Mechanica, 1975, 21(3):173-192.DOI: 10.1007/BF01181053.
[13]SHEN C P, MAMAGHANI I, MIZUNO E, et al. Cyclic behavior of structural steels. II: theory[J]. Journal of Engineering Mechanics, 1995, 121(11):1165-1172.
[14]IURA M, KUMAGAI Y, KOMAKI O. Ultimate strength of stiffened cylindrical shells subjected to axial and lateral forces[J]. Journal of Structural Mechanics and Earthquake Engineering, 1997, 556(I-38):107-118.
[15]GE Hanbin, GAO Shengbin, USAMI T. Stiffened steel box columns: part 1 cyclic behavior[J]. Earthquake Engineering & Structural Dynamics, 2000, 29(11):1691-1706.DOI:10.1002/1096-9845(200011)29:11<1691::AID-EQE989>3.0.CO;2-U.
[16]陈绍蕃. 钢结构稳定设计指南[M]. 北京:中国建筑工业出版社, 2004: 264-267.
(编辑 魏希柱)
Ductility prediction of stiffened steel pipe-section bridge piers
LIU Naifan, GAO Shengbin
(School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China)
To investigate the nondimensionalized ultimate strength and ductility behavior of stiffened steel pipe-section bridge piers subjected to a constant vertical load and cyclic lateral loads, the modified two-surface constitutive model and its finite element modeling were verified by comparing with the test results, and the effects of radius-thickness ratio, pier’s slenderness ratio, stiffener’s slenderness ratio and axial load ratio of the piers with eight stiffeners were investigated on the nondimensionalized ultimate strength and ductility. Some formulas based on the parametric analytical results were proposed to predict the nondimensionalized ultimate strength and ductility of piers. Numerical simulation results show that the nondimensionalized ultimate strength and ductility behaviors of the steel bridge piers could be notably improved when decreasing of radius-thickness ratio, pier’s slenderness ratio, stiffener’s slenderness ratio and axial load ratio.
bridge engineering; steel bridge piers; modified two-surface model; nondimensionalized ultimate strength; ductility behavior
10.11918/j.issn.0367-6234.2017.03.022
2016-06-22
上海市科学技术委员会浦江人才计划(08PJ1406400)
刘乃藩(1990—),男,硕士; 高圣彬(1970—),男,副教授,博士生导师
高圣彬,gao_sb@sjtu.edu.cn
U443.22
A
0367-6234(2017)03-0138-06

