AASL策略透视代数应用情境的数学本质

田献增++魏淑玲�お�

【摘要】代数应用题是中小学数学主流问题、难点课题，是发展学生数学核心素养的重要素材.AASL策略通过引入核心概念“基本数量关系”，借助分类思想，给出了揭示其数学本质的普适性方法，诠释了《课标》问题解决中有关模块的“基本方法”.

【关键词】AASL策略；数学本质；基本数量关系；核心素养；基本方法

问题解决是数学的核心问题[1].在中小学数学中，代数应用题是问题解决的主流问题.“‘怎样解数学应用题是從小学就开始的一个难点课题”[2].其根源或许是缺少系统完整的揭示承载具体问题的代数应用情境数学本质的程序和方法.田献增老师以教育数学[3]思想为指导，构建的“代数应用情境学习策略”[4，5]（即：Algebra Application Situation Learning Strategy.为叙述方便，下文简称“AASL策略”，《中国数学教育》2014年第12期中称之为“DYQ学习策略”），从揭示数学本质出发，构建了系统完整的中小学应用题审题方法，使八成左右的应用题审题方法统一了起来[5].

1数学本质与代数应用情境的数学本质

1.1数学本质

对于数学本质的认识，数学家、数学哲学家一直没有统一的结论[6].张奠宙教授认为，数学本质即数学知识的内在联系、数学规律的形成过程、数学思想方法的提炼和数学理性精神的体验.数学本质的多元性[6]决定了数学本质有广义与狭义、整体与局部之分.张景中院士认为，小巧一题一法，固不应提倡，大巧法无定法，也确实太难，实时提倡“中巧”.所谓中巧，就是能有效地解决一类问题的算法或模式.如果没有中巧，就要靠数学家研究创造一些“中巧”.笔者认为之所以“中巧”可以解决同类问题，原因是这一类题目的数学本质是相同的.

1.2代数应用情境的数学本质

不可置疑，代数应用情境的数学本质是情境中的数量关系.这是因为，同一个代数应用情境中，问题是可变的，已知数和未知数是可变的，解决的具体问题需要的纯数学理论知识是可变的，而代数应用情境中的数量关系是不变的.

另外，解决同一个代数应用情境的同一个问题时，不同模型获得的分析过程（或解决同一类代数应用题时，模型获得的分析过程）是可以同构的，揭示其“共性”或“规律”的方法是具有共性的，也就是说揭示该类代数应用情境的数学本质应是具有“通式通法”的.

但纵观代数应用题的教学设计和学生的学习过程可以发现：数学理论体系中往往关注的是纯数学知识，如方程、方程组、不等式、函数等等；对揭示“代数应用情境”数学本质的方法，虽然前人已经做了大量的工作，但似乎还可以从更高的角度，利用已有的成果构建概念更直观、逻辑结构更简单、方法更有力的通用工具[7]，以此揭示代数应用情境的数学本质.

2AASL策略的内涵

自上世纪八十年代末，张景中院士提出了教育数学思想，在教育数学思想的影响下，涌现出了大批优秀成果.针对中小学数学应用题的审题环节建构的AASL策略就是其代表之一.它包含以下要点：

（1）该策略根据应用题中常见“关键词”，把数学语言划分成三类，即：数量的大小比较、数量的倍分比、数量的大小比较和倍分比，并明确了每一类数学语句的分析方法.

（2）该策略根据代数应用题中常见的数量关系的呈现形式、应用方法，将数量关系分为直译型数量关系、基本数量关系、公式型数量关系；并在此基础上，给出了清晰的识别标准、系统完整的分析模式和程序.

（3）该策略抓住行程问题的“动态”特点，引入了“运动过程图”概念，明确规范了运动过程图的画法，突破了理解行程问题的瓶颈.

（4）该策略针对在生活数学情境中，广泛存在且具有本原性特点的、形如“a×b=c”的数量关系，引进了“基本数量关系”的概念，将普遍存在的类似于“速度×时间=路程”、“单价×数量=总价”、“工作效率×工作时间=工作量”等数量关系给予统一.针对新概念——“基本数量关系”具有反复应用的特点，引入了“分类思想”，给出了具有“大众化”特点的、本原性方法——“分类列表”的通用模式.

（5）该策略针对数量关系存在的形式，重新明确了应用题的分类标准.将中小学代数应用题分为——“直译型”、“基本数量关系型”和“公式型”应用题.对于每一类应用题，为学生提供了清晰的识别标准和审题方法，使每一类问题的审题有了明确的突破口.

该策略共分五个模块，即“怎样分析数学语句”、“怎样分析数量关系”、“怎样画运动过程图”、“基本数量关系与分类列表”、“数学建模程序介绍”，按照先分后总的思路，介绍了获得数学模型“前期”的首要方法和技能.（详见文[4]）

AASL策略解决的问题是中小学应用题的审题或分析题意的过程和方法，其核心概念是“基本数量关系”，核心方法是根据基本数量关系“分类列表”.它是解答代数应用题前期必备的“基础知识”、“基本技能”和“首要方法”.

3AASL策略与代数应用情境的数学本质

下面结合2015年浙江省绍兴市中考数学试题第16题说明如下：

3.1引例图1

实验室里，水平桌面上有甲、乙、丙三个圆柱形容器（容器足够高），底面半径之比为1∶2∶1，用两个相同的管子在容器的5cm高度处连通（即：管子底端离容器底5cm），现三个容器中，只有甲中有水，水位高1cm，如图1所示.若每分钟同时向乙和丙注入相同量的水，开始注水1分钟，乙的水位上升56cm，则开始注入分钟的水量后，甲与乙的水位高度之差是05cm.

说明本题背景来源于学生熟悉的实验室里连通器，因此给人们的第一感觉是一道学科综合性问题.分析题意时容易想到物理学中的“压强”、“毛细现象”、“连通器原理”等.之所以出现这样的偏差，或许与古今中外在数学教育中，缺少揭示代数应用情境数学本质方法上的研究有直接关系.

3.2AASL策略透析引例的数学本质

算术法由“开始注水1分钟，乙的水位上升56cm”可想到本题含有基本数量关系：“1分钟升高的高度×分钟数=升高总高度”，因此本题属于“基本数量关系型”问题，可套用“AASL策略”的核心方法“分类列表”进行分析.过程如下.

首先，由基本数量关系“1分钟升高的高度×分钟数=升高总高度”知，本题是“基本数量关系型”问题.

其次，根据题中“底面半径之比为1∶2∶1”等信息可知，本题与圆柱的体积公式有关，所以准确回忆圆柱的体积公式——V=πr2h是必经的审题过程.

结合基本数量关系可知，需要考虑甲、乙、丙三管“1分钟升高的高度”.

设甲、丙两管的半径都为1，乙管半径为2，则圆柱体积分别为

V甲（丙）=πh，V乙=4πH.

若把V看做一分钟注水量，则由比例可知h∶H=4∶1，因此甲、丙两管分别注水1分钟水位升高的高度都是乙管的4倍，即56×4=206cm.

另外，由题意知，丙管外溢后，乙管注水1分钟水位升高的高度应为：56×2=106cm.

乙外溢后，注水1分钟甲管水位升高的高度是406cm.

因丙、乙两管存在外溢的事实，所以需要考虑乙、丙外溢时的有关数量.也就

是说审题时需要注意丙、乙外溢时两个节点.

由“甲与乙的水位高度之差是05cm”可知，本题需借助分类思想进行分类讨论（即“甲比乙高05cm”和“乙比甲高05cm”两种情况）.因给出的情境是学生熟知的实验室连通器.从宏观上看，需要考虑乙管外溢前和乙管外溢后两种情况，而乙管外溢前又需考虑“甲比乙高05cm”和“乙比甲高05cm”两种情况.对于乙管外溢后的情形，只需考虑“乙比甲高05cm”的情形.最后，结合基本数量关系分类列表如表1：表1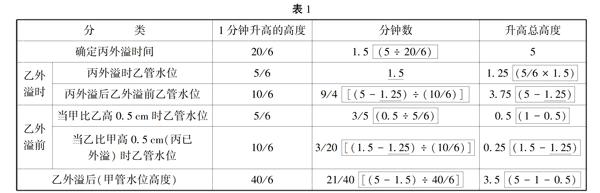

綜合上述可得算术法解题过程.（下略）

说明：（1）表1框中算式均由同行中另外两数或算式相乘或相除得到.除此之外，表中下划线数据均来源于表中前面已经计算获得的数据.（2）表1是在基本数量关系导引下，结合数学中的“分类思想”完成的.利用表1同样可以获得方程法、函数法等.

方程法1当表1中相应阶段对应的时间设为xmin时，（注意：表2中每一行中的x的含义是不同的），且将水管“升高高度”利用“1分钟升高的高度”与x表示后，填表如下.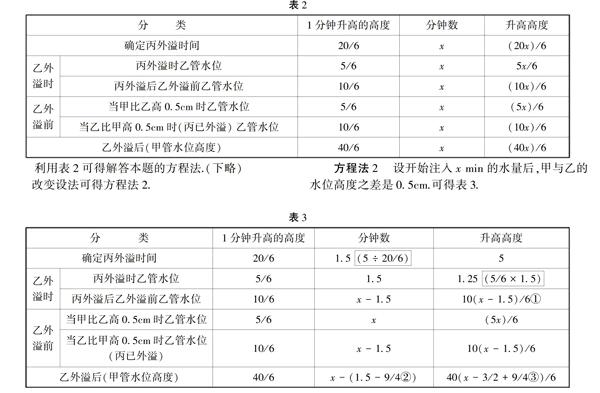

结合题意和表3可得本题的另一种方程解法.（下略）

函数法用函数的观点看，设x min后甲、乙两管的水位高度分别为y甲（cm）、y乙（cm），同样可以利用表3，分别建立函数关系式，然后根据对应的函数值求自变量x即可.（下略.利用表2，也可得函数解法）

3.3对代数应用情境的数学本质思考

从引例不同解法的分析过程可以看出：

（1）上述表格结构是完全相同的，不同之处是数据填写方法或处理数据的方法.

（2）对于同一类方法（算术法、方程法或函数法）呈现的数学模型之所以不同，原因是对同一张表格中的数据，加工处理的方法不同.

（3）对于函数法来说，表中数据与方程法表中的数据完全相同，不同的是分别运用了方程思想、函数思想.

（4）从（3）中看出，数学理论层次不同，导致表格中数据的填写顺序、处理方式也不尽相同，但本质是相同的.

（5）对于复杂的问题，在分析实际问题时，常常需要边建模、解模，边填写表格中数据（如表1中的带有下划线数据，表3中的数据②③）.

（6）事实上，算术法、方程法或函数法对应的数学模型又分别可有若干种，但从分析题意或审题的角度看，这些不同的方法都可在基本数量关系的引领下，运用“分类思想”进行分类列表实现.

类比引例不难得出：对于同一个代数应用题，不管利用什么样的数学模型解决，分析题意的方法是可以统一的；事实上，对于同一类代数应用题，不管利用什么样的数学模型解决，分析题意的方法同样是可以统一的.显然，要获得这一通式通法的前提，必须抓住承载具体问题的代数应用情境数学本质.4AASL策略价值分析

4.1AASL策略是人们生活经验的积累，是对已有成果的发展与整合

“数学既不像有些数学家所认为的是同经验无关的纯逻辑体系，也不完全是经验的总结.”[6]“凡吾人之一切知识，皆以经验始.（康德语）”AASL策略也不是无源之水、无本之木，同样是将人们的生活经验（如案例清点人民币.见文[5]）提炼为非传统意义上的数学方法，是对已有成果的改造与整合.

4.2AASL策略是对中小数学教学难点的突破

因为AASL策略引入核心概念“基本数量关系”后，借助核心方法“分类列表”，同构了80%左右的应用题或问题解决的审题方法.其核心概念和核心方法是“从平凡之处寻求的创新”，通过新定义新概念，提出的新问题新技巧，建立的新方法新体系.起点低，观点高，适宜从义务教育阶段的低年级开始渗透施教，在高年级强化训练，小学阶段系统掌握，在初中阶段当做数学“工具”使用.这无论从学生学习数学的时间、精力上考虑，还是从学生对数学学习心理上考虑，在数学教育中，或将产生积极的意义和影响.

4.3AASL策略是发展学生数学核心素养的有效途径

在2014年3月教育部印发的《关于全面深化课程改革、落实立德树人根本任务的意见》中，明确把“核心素养”作为各学科课程目标和教学要求的重要依据.因为“数学素养”与“阅读素养”、“科学素养”并列成为PISA测试的三大领域，因此数学学科在提升学生数学核心素养中显得尤为重要.

目前，对于数学核心素养的表述，尽管有所不同，但通过“数学建模”、“模型思想”发展学生的数学核心素养是大家的共识.从这个角度看，AASL策略的构建，对于在中小学数学教学或学习中，落实教育部《意见》，发展学生的数学核心素养也将产生积极的作用.

4.4AASL策略是对《课标》问题解决中相关模块的基本方法的尝试说明

我们知道，义务教育数学课程标准（2011年版）首次要求“使学生体验从实际背景中抽象出数学问题、构建数学模型…的过程”、“获得分析问题和解决问题的一些基本方法”等等.因为AASL策略给出的是解决实际问题、构建数学模型的普适性方法，所以从某种意义上说，AASL策略用教育数学的思想诠释了《标准》问题解决中相关模块的基本方法[5].

参考文献

[1]喻平.数学问题解决认知模式及教学理论的研究[D].南京：南京师范大学，2002，2.

[2]罗增儒.数学解题学引论[M].西安：陕西师范大学出版，2016.

[3]张景中，曹培生.从数学教育到教育数学[M].北京：中国少年儿童出版社，2005.

[4]田献增.数学慧眼[M].成都：电子科技大学出版社，2013.

[5]田献增，李忠海.大道至简，悟者天成[J].中国数学教育.2014（12）：1-5.

[6]曹一鸣.从数学本质的多元性看数学教育的价值[J].中国教育学刊，2005，2.

[7]张景中.什么是教育数学[J].高等数学研究，2004，2：2-6.

[8]义务教育数学课程标准（2011年版）[S].北京师范大学出版社.2012.

作者简介田献增（1963—），男，山东日照人，中学高级教师，AASL策略创始人.主要研究教材教法、代数应用题等.著有《数学慧眼》、《中考数学十大突破》等.