Practical Polar Code Construction For Degraded Multiple-Relay Networks

Bin Duo, Xiaoling Zhong , Yong Guo

College of Information Science & Technology, Chengdu University of Technology, Chengdu 610059, China

* The corresponding author, email: zhongxl@cdut.edu.cn

I. INTRODUCTION

The extension of network information theory and coding to cooperative communication networks has been enormously developed in recent years. Relaying as one of the most effective technique of cooperative transmission in wireless networks receives particular attention [1,2]. The classical three-node relay network is a scenario in which the relay node only helps forward source messages as reliable as possible to the destination node without sending its private messages [3]. For the degraded single-relay network, the capacity is obtained in [4] using the decoded-and-forward(DF) strategy. This capacity has been achieved by several powerful encoding and decoding schemes developed in [4-6].

Practically, more than one relay node exists in real-life communication networks. The previous encoding and decoding schemes based on the DF strategy used in the single-relay networks have been directly generalized to multiple-relay networks in [7-9]. Later, a new parity forwarding protocol and a novel decoding scheme have also been proposed in [10]that can achieve the capacity of the degraded multiple-relay networks. All the above-mentioned coding schemes, however, focus on the derivation of the lower/upper capacity bounds of multiple-relay networks by using random coding schemes. It has theoretically indicated that there exist capacity-achieving codes, but how to construct practical codes with realizable complexity to achieve the capacities of multiple-relay networks still remains an open problem.

Polar codes have recently been paid close attention in coding territory because they can achieve the capacity of symmetric binary-input discrete memoryless channels (SBDMC).Moreover, the encoding and the decoding

In this paper, based on nested polar codes,the authors proposed a generalized partial information relaying protocol for the degraded MRN-ORCs.complexity of polar codes are as low aswhereis the Landau notation andNis the block length. At first, polar codes were applied in the point-to-point channel and the theoretical bounds were extensively studied in [11-15]. The performance of polar codes in practical situation was also investigated and significantly improved in [16-20].Later on, polar codes were applied in certain multi-user systems, such as broadcast channels [21], multiple-access channels (MAC)[22,23] and single-relay networks [24-26]. To our knowledge, the potential of employing the remarkable characteristics of polar codes and designing corresponding transmission protocols for multiple-relay networks still remains a challenging problem.

In this present paper, based on the nested structure of polar codes, a class of new DF strategies named generalized partial information relaying protocol is developed for the degraded multiple-relay networks that have orthogonal receiver components (MRN-ORCs)as an extension of our previous work on a specific protocol for the two-relay network in[27]. In the previous paper, we only consider the specific protocol and the corresponding polar coding scheme for the two-relay channel.Also the channel is a simplified model of the general two-relay channel without the channel between the source node and the second relay node. This paper provides contributions beyond those of the previously published work as follows:

1) The partial information relaying protocol is extended to the general degraded two-relay network. In this generalized protocol, relay nodes first decode the received source message and then flexibly forward part of the decoded message according to the partial information that the following relay node or the destination node needs. After receiving all the partial information, the intermediate relay nodes or the destination node combine the available and helpful information to decode the source message by performing the successive cancellation (SC) decoding.

2) Then the two-relay case is generalized to the multiple-relay case. To satisfy the efficiency of communications, the information sets of nested polar codes are designed depending on the characteristic of the networks. This indicates that the designed code rate achieves the theoretical capacity with any small error probability of the degraded MRN-ORCs and meanwhile keeping low complexity.

3) The proposed scheme provides a flexible and low-complexity scenario for ensuring reliable transmissions over multiple-relay networks. The proposed scheme generalizes the counterparts in the original single-relay networks in [24,25] and the previous two-relay network in [27].

4) The simulation results present the practical performance of nested polar codes in binary symmetric channels (BSC) with moderate block lengths for the generalized partial information relaying. Compared with the conventional low-density parity-check(LDPC) coded schemes, the results show that the obtained polar codes by using successive-cancellation list decoder (SCLD)with cyclic redundancy check with 16 bits(CRC-16) proposed in [20] achieves better performance.

II. BACKGROUND AND SCENARIO

2.1 Degraded multiple-relay networks

The general model of multiple-relay networks consists of a pair of source and destination nodes and a number of intermediate relay nodes. The relay nodes transmit no private messages and only forward messages received from the source node and previous relay nodes. Moreover, the direct link between the source node and the destination node exists in this model. One of the main objectives is to help the destination node to resolve the uncertainty about the received source message.Consider the network withnodes in which the source node is denoted by index 0(i.e.,the destination node is represented by indexand the relay nodes are denoted sequentially from 1 toKLet random variabledenote the input to the network,be the ultimate network output,denote the relay inputs andbe the relay outputs, respectively, for the corresponding nodes. The network is described by the conditional probability mass function(pmf)whereandare the realizations of the random variablesandrespectively.

The theoretical coding scheme for the general multiple-relay network to guarantee a reliable communication with arbitrary small probability of error has been formulated and studied in detail in [8], where the DF strategy is proved to be capacity-achieving under the degradedness condition for this network. The following theorem summarizes the capacity achieved by using this strategy.

Theorem 1([8]): A general discrete memoryless multiple-relay network is said to be degraded if

Since the coding scheme and the corresponding transmission protocol are primary concern in the following paper, the model of MRN-ORCs is considered for simplicity. The scenario can be extended to general multiple-relay networks when receivers with optimized multiple-user signal detection are used,which is beyond the scope of this paper.

The behavior of the MRN-ORCs is formulated by the pmf as

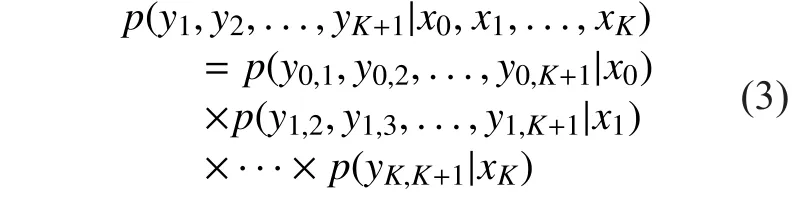
Generally, the overall system of the proposed MRN-ORCs as illustrated in Fig.1 works as follows. The source nodefirst encodes the message vectorinto a length-Ncoded vector denoted byand then broadcasts it into the network. Upon receivingthe relay nodetries to recover the source messageand generates a length-Ncoded vector denoted bywhich is transmitted into the network. Similarly, foris a vector of lengthNput into the network by the relay nodeandare the observations at nodeAfter that, the destination nodewishes to recover the original messagefrom its observations which is denoted byThe corresponding estimate atis denoted byThe final objective is to design a practical coding scheme with realizable complexity as well as a corresponding DF strategy that guarantees reliably delivery oftowith the help of relays at a rate as high as the capacity of the network.

Fig. 1 Multiple-relay network with orthogonal receiver components

For the degraded MRN-ORCs, the average probability that the destination nodemakes an error in recoveringis defined as

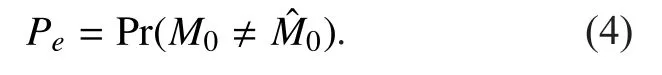
The following theorem provides the capacity of the degraded MRN-ORCs considered in this paper in an explicit form.

Theorem 2: The capacity of the degraded MRN-ORCs by using DF strategy is given by

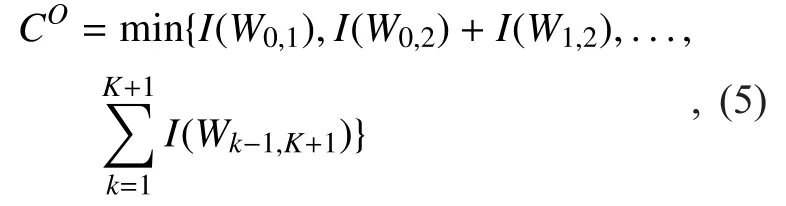
Proof:According to the result of Proposition 2 in [28], Equation (2) can be rewritten as

It can be observed from [29] that all the mutual information terms in Equation (6) are concave functions ofwhereare the realizations ofrespectively. The maximum can be achieved whenare all uniformly distributed. Therefore, Equation (6)can be simplified as Equation (5), which completes the proof.

2.2 Nested polar codes

The phenomenon of channel polarization is the key idea of polar codes, and polar codes are the natural consequence of the channel polarization. Channel polarization includes two operations: channel combining and channel splitting. As noted in [11], define a SBDMCsatisfyingwhereandis theNindependent uses ofIf the source informationcan be encoded by the generator matrixGdefined in [11] asthe synthesized channel represented byis given byThis operation is called the channel combining. The operation of the channel splitting is to transforminto a set ofNparallel polarized channels, defined by [12]

AsNgrows large enough,polarizes either a pure-noise or a noiseless channel. From[11,12], the key results of channel polarization can be summarized precisely by the following theorem.

Theorem 3([11,12]): ForNSBDMCsWand fixedpolarizes as below,

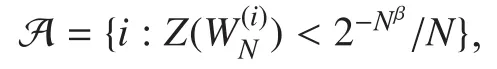
Also the polar coding result under the SC decoding with low-complexity ofis evaluated by the average error probabilitywhich is upper bounded by

It can be observed from [12] that polar codes can be constructed for degraded broadcast channels with two terminals. This signifi-cantly important result can also be extended to degraded broadcast channels with multiple terminals as detailed in Lemma 1 below.

Lemma 1: LetbeqSBDMCs forwithThe information set foris denote byThus, we have

Proof.The proof follows directly from that in [12] by induction.

The existence of the nested property of information sets for constructing polar codes is a general phenomenon for the degraded broadcast channels with multiple terminals.When the channel polarization occurs, all the polarized channels that are noiseless forare also noiseless for any other better channelHowever, the polarized channels that are noiseless for the better channelmay not be noiseless for

III. NESTED POLAR CODING SCHEME

By utilizing the result proved in Lemma 1, in this section, we can design a generalized partial information relaying protocol based upon nested polar codes to achieve the capacity in Equation (5). To make it easier to follow,we first consider the two-relay case that contains all the fundamental ideas. Note that the scheme using DF strategy forin [24,25]can be directly deduced from the following discussed case forThen we present the straightforward extension to the general case for

3.1 Two-relay case

Assume that the proposed scheme for the two-relay network that has orthogonal receiver components (TRN-ORCs) is applied for communication satisfyingandThen, the corresponding information sets as in Lemma 1 satisfy

Fig. 2 Partial information relaying based on nested polar codes for the TRN-ORCs

In this system as shown in Fig.2, the source messagewith information setis firstly broadcast to the nodesandBecause of the serial degradation assumptions,andcan only obtain part ofcorresponding to the setandinrespectively.Similarly, the partial message atdenoted bywithis to be transmitted toand to be degraded fromsocan only receive part of information corresponding toinFinally, the partial message atdenoted bywithis to be sent toto resolve the residual uncertainty ofFrom the discussion above, the construction of nested polar codes atandcan be described as shown in Table I.

From Lemma 1, we note that since all the noiseless polarized channels forare also noiseless for better channelsandwhen constructing polar codes,is also the information set forandbesidesFromwe also know that(i.e., the set inbut not inis not only the information set forbut also the information set for the better channelOn the contrary,is the set that consists of noisy polarized channels for the worse channelwhich can be seen as the corresponding frozen set. Similarly,is only the information set for the best channelbut is the frozen set for the degradedchannelsand

Table I The nested structure of information sets for polar codes atand

Table I The nested structure of information sets for polar codes atand

We use the block Markov coding scheme[4] and letNrepresent each length of the transmittedBcodewords inB+1 blocks. As is shown in Fig.2, it is assumed that the source nodetransmits a messagein blocktforwhich can be divided into three independent vectors corresponding to the construction of the nested structure, i.e.,andrespectively. Let andbe the messages transmitted at N1and N2in blockt+1 and blockt+2, respectively, and they are the partial messages of the previous receivedMathematicallyandare computed by

The algorithm for computing the partial information sets are described in the following algorithm 1.

3.2 Multiple-relay case

The partial information relaying protocol can be generalized to MRN-ORCs by allowing relay nodes to transmit part of the decoded source message from the source node or other relay nodes. The key step in such a structured generalization is to identify the relation among information sets.

We still use the block Markov coding argument and consider transmission ofBcodewords of lengthNinB+1 blocks. In blocktfor, the source messageatcan be partitioned intoK+1 independent vectors, i.e.,wherebe the partial message oftransmitted at Nkin blockwhich can be computed by

which can be computed accordingly as Algorithm 1. We note thatalso partitioned into independent vectors corresponding to the partial information sets as the source message

Since the proposed partial information relaying protocol depends on the original nested polar coding arguments, the encoding complexity is as low asfor MRN-ORCs. Moreover, ifWk,l, for 0≤k≤Kandk+1≤l≤K+1, are all BECs in MRN-ORCs, the construction complexity of polar codes is only

Algorithm 1: Computation of the partial information sets

Table II The nested structure of polar codes at.

Table II The nested structure of polar codes at.

IV. ANALYSIS OF CAPACITY AND ERROR PROBABILITY

In this section, we provide a rigorous analysis to show that, by constructing nested polar codes, the generalized partial information relaying protocol can asymptotically achieve the capacity of the degraded MRN-ORCs in Equation (5) with vanishing error probability.

4.1 Capacity analysis

For the generalized partial information relaying protocol, the encoding and decoding process at theK+1 nodes as shown in Table III are performed in block-wise as below.

At the end of blockt+K, by combining all the helpful partial information transmitted by relay nodes,can regain the sourcemessagefromTo decodewe consider it as a codewordsent fromtoin blockt. Therefore, a decreased rate is obtained as

Table III The encoding and decoding process for the generalized partial information relaying protocol.

According to the analysis specified above,we provide the main result of this paper that the designed rate of nested polar codes for the generalized partial information relaying protocol asymptotically achieves the capacity of the degraded MRN-ORCs, which is given as below.

Theorem 4: A polar coding rateis said to be achievable for a degraded MRNORCs, if the average block error probabilityby SC decoding satisfiesfor anyand sufficiently largeN.

The proof of this theorem is given in the next subsection. We note that as the proof of Theorem 4 is asymptotically achieved by using the SC decoding, the proposed scheme keeps the decoding complexity as low asMoreover, when settingK=1, the main result obtained in this generalized case is the results proved in Theorem III.1 in [24] and in Theorem 1 in [25]. By settingK=2, we generalize the achievability result of the two-relay network in Theorem 2 in [27] when the channel distance from the source to the second relay is far away such thatis blocked.

4.2 Analysis of the error probability

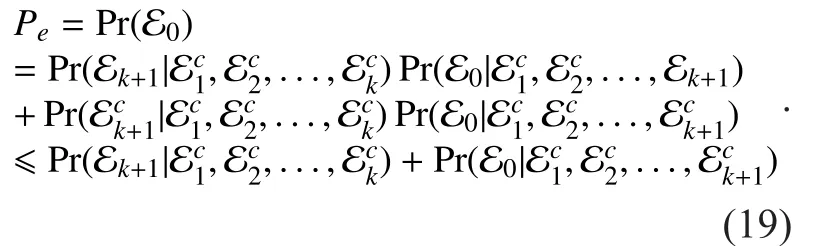
The first term in Equation (19) means the error probability of estimatingwhen all the previous nodes are correctly decoded. If the polar coding rate satisfieswe can obtain the result from Equation (10) that

The second term is the error probability of decodingwhen the destination node combines all the partial information transmitted from preceding relay nodes. Hence, for any ratethe same bound can also be applied tosuch that

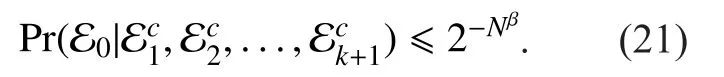
Consequently, by recursively collecting all the terms in Equation (20) and Equation (21),the overall error probability at the destination node over allBblocks is upper bounded byprovidedThis finalizes the proof of Theorem 4.

V. SIMULATION RESULTS

In this section, the practical performance of nested polar codes with moderate block lengths is evaluated for partial information relaying by simulations.

We consider the degraded TNR-ORCs as an example. All the channel links in TNR-ORCs are independent BSCs. The capacity of each BSC link is computed according to the terms in Equation (5) forK=2. We use the simulation specification that is listed in Table IV in the following simulations. Hence, the capacity of the degraded TRN-ORCs equals to that of.That is,

For fast and effective implementation, the Monte Carlo method is used to design polarcodes as described in Section III. Though we let the total number of transmission blocks bethe impact on the source transmission rateis small when the block lengthNis large. For the decoder, SC decoding algorithm is firstly used in the simulations because of its theoretical optimum and low implementing complexity.

Table IV Simulation parameters

We first study the case whenis a noiseless channel withFig.3 illustrates the bit error rate (BER) results of decodinggiven different transmission rates of the sourceand the second relayIt can be seen from the figure that the BERs drop obviously by increasingnand also by reducingwhich means that the proposed scheme has the potential to achieve the capacity with appropriate design. Moreover, a lower BER is also observed by increasingThe reason for this fact is that the destination node receives correct partial information from the first relay node and the second relay node, asis a totally error-free channel, andandare regarded as nearly noiseless channels because of high capacities and much lower transmission rates. If the relay nodes can forward partial information with more reliability,the destination node has more capability to solve the uncertainty ofby combing these helpful partial information. By increasingthe second relay node can help forward more reliable information to the destination node,and correspondingly, the amount of received information fromthat has to be decoded is reduced. Therefore, the BER improves significantly.

Fig. 3 BER versus R0 and R2 when W2,3 is error-free

We now consider the case whenis a BSC. As is shown, the BERs improves again with largernor with lowerHowever, in this case error floor happens and we cannot improve the BER by increasingThis is because some bits in the partial information that the second relay node forwards over the channelflip which result in errors. The occurrence of these error bits plays a dominant role on the performance of decoding the useful partial information forwarded by the second relay node. This information is essential to help recoverfromHence, the weakness ofbrings a larger BER at the destination node which cannot be improved significantly by decreasing

In Section IV, it has been proved that the developed scheme is asymptotically capacity-achieving asHowever, from the observation of the simulation results in Fig 3 and Fig.4, the BERs by using the SC decoding does not lower fast enough. This problem can be improved by using other decoding algorithms, such as the SCLD derived in [20]. Fig.5 illustrates the performance of polar codes under SC decoder and SCLD with list sizeL= 32 and CRC of 16 bits long. Simulation parameters are the same as in Fig. 3 forIt can be seen from Fig. 5 that the proposed scheme by using SCLD with CRC-16 provide much better performance over that of using the SC decoder. Moreover, we also compare the performance of the conventional LDPC scheme with similar simulation parameters for the relay systems proposed in [33]. Belief propagation decoding with up to 200 is used.It is shown that the performance of the proposed scheme using SCLD with CRC-16 outperforms the one using state of the art LDPC codes. For polar codes with SCLD, the time complexity isin contrast withcomplexity of SC decoder, but the space complexity is reduced fromto. As another advantage over conventional LDPC codes, polar codes have lower encoding complexity.

VI. CONCLUSIONS

In this paper, based on nested polar codes, we have developed a generalized partial information relaying protocol for the degraded MRNORCs. Specifically, we have provided insights on how to construct the nested structure of partial information sets and design the corresponding polar codes at the source and relay nodes. It has shown that the proposed scheme theoretically achieves the capacity of the network. Moreover, simulation results validate the construction of nested polar codes for generalized partial information relaying, so that the obtained polar codes with SCLD provide noteworthy gain with respect to the similar LDPC codes. In order to ensure reliable transmissions over multiple-relay networks, the proposed scheme has provided a flexible and low-complexity scenario. Many of the previous results for the original single-relay and two-relay networks with polar coding schemes can be recovered as special cases of the results presented in this paper. Although the SBDMC case is considered in this paper, the practical applications of the proposed scheme for fading channels in multiple-relay networks are also an interesting problem, which we leave the analysis to our future work.

ACKNOWLEDGEMENTS

This research work is supported by the National Natural Science Foundation of China(No. 41574137, 41304117).

[1] Y.C He, J.J Zhang, R. Zhao,et al, “Iterative Noncoherent Block Detection of Coded MPSK for Cooperative Relay Systems,”China Communications, vol.13, no.7, pp.1-6, July 2016.

[2] Z.W Zhang, Y.Z Li, K.Z Huang,et al, “Energy Efficiency Analysis of Cellular Networks with Cooperative Relays via Stochastic Geometry,”China Communications, vol.12, no.9, pp.112-121, September 2015.

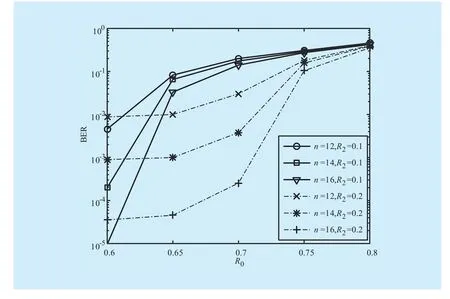
Fig. 4 BER versus R0 and R2 when W2,3 is a BSC

Fig. 5 Performance comparison of polar codes with different decoders and LDPC codes

[3] E.C Van der Meulen, “Three-terminal Communication Channels,”Advanced Applied Probability,vol.3, pp.120-154, March 1971.

[4] T. Cover, A.E Gamal, “Capacity Theorems for the Relay Channel,”IEEE Transactions on Information Theory, vol.25, no.5, pp.572-584, September 1979.

[5] A. Carleial, “Multiple-access Channels with Different Generalized Feedback Signals,”IEEE Transactions on Information Theory, vol.28, no.6,pp.841-850, November 1982.

[6] F. Willems, E.C Van der Meulen, “The Discrete Memoryless Multiple-access Channel with Cribbing Encoders,”IEEE Transactions on Informa-tion Theory, vol.31, no.3, pp.313-327, May 1985.

[7] P. Gupta, P.R Kumar. Towards an Information Theory of Large Networks: an Achievable Rate Region,”IEEE Transactions on Information Theory, vol.49, no.8, pp.1877-1894, August 2003.

[8] L.L Xie, P.R Kumar, “An Achievable Rate for the Multiple-level Relay Channel,”IEEE Transactions on Information Theory,vol.51, no.4, pp.1348-1358, April 2005.

[9] G. Kramer, M. Gastpar, P. Gupta, “Cooperative Strategies and Capacity Theorems for Relay Networks,”IEEE Transactions on Information Theory, vol.51, no.9, pp.3037-3063, September 2005.

[10] P. Razaghi, W. Yu, “Parity Forwarding for Multiple-relay Networks,”IEEE Transactions on Information Theory, vol.55, no.1, pp.158-173,January 2009.

[11] E. Arikan, “Channel Polarization: a Method for Constructing Capacity Achieving Codes for Symmetric Binary-input Memoryless Channels,”IEEE Transactions on Information Theory, vol.55,no.7, pp.3051-3073, July 2009.

[12] S.B Korada. Polar Codes for Channel and Source Coding. Lausanne: EPFL, 2009.

[13] E. Arikan, E. Telatar, “On the Rate of Channel Polarization,”2009 IEEE International Symposium on Information Theory (ISIT), pp.1493-1495,2009.

[14] S.B Korada, R. Sasoglu, R. Urbanke, “Polar Codes: Characterization of Exponent, Bounds,and Constructions,”IEEE Transactions on Information Theory, vol.56, no.12, pp.6253-6264,December 2010.

[15] V. Guruswam, P. Xia, “Polar Codes: Speed of Polarization and Polynomial Gap to Capacity,”IEEE Transactions on Information Theory, vol.61, no.1,pp.3-16, January 2016.

[16] R. Mori, T. Tanaka, “Performance of Polar Codes with the Construction Using Density Evolution,”IEEE Communications Letters, vol.13, no.7,pp.519-521, July 2009.

[17] E. Arikan, “Systematic Polar Coding,”IEEE Communications Letters, vol.15, no.8, pp.860-862,August 2011.

[18] A. Eslami, H. Pishro-Nik, “On Finite-length Performance of Polar Codes: Stopping Sets, Error Floor, and Concatenated Design,”IEEE Transactions on Communications, vol.61, no.3, pp.919-929, March 2013.

[19] G. Sarkis, P. Giard, A. Vardy,et al, “Fast List Decoders for Polar Codes,”IEEE Journal on Selected Areas in Communications, vol.34, no.2, pp.318-328, February 2016.

[20] I. Tal, A. Vardy, “List Decoding of Polar Codes,”IEEE Transactions on Information Theory, vol.61,no.5, pp.2213-2226, May 2015.

[21] N. Goela, E. Abbe, M. Gastpar, “Polar Codes for Broadcast Channels,”IEEE Transactions on Information Theory, vol. 61, no.2, pp.758-782,February 2015.

[22] R. Nasser, E. Telatar, “Polar Codes for Arbitrary DMCs and Arbitrary MACs,”IEEE Transactions on Information Theory, vol.62, no.6, pp.2917-2936, June 2016.

[23] E. Sasoglu, E. Telatar, E.M Yeh, “Polar Codes for the Two-user Multiple-access Channel,”IEEE Transactions on Information Theory, vol.59,no.10, pp.6583-6592, October 2013.

[24] M. Andersson, V. Rathi, R. Thobaben,et al,“Nested Polar Codes for Wiretap and Relay Channels,”IEEE Communications Letters, vol.14,no.8, pp.752-754, August 2010.

[25] R. Blasco-Serrano, R. Thobaben, M. Andersson,et al, “Polar Codes for Cooperative Relaying,”IEEE Transactions on Wireless Communications,vol.60, no.11, pp.3263-3273, November 2012.

[26] A. Bravo-Santos, “Polar Codes for Gaussian Degraded Relay Channels,”IEEE Communications Letters, vol.17, no.2, pp.365-368, February 2013.

[27] B. Duo, Z.Y Wang, X.M Gu, “Cooperative Partial Message Relaying Based on Distributed Polar Codes for the Two-relay Network,”2012 International Conference on Sensors, Measurements and Intelligent Materials (ICSMIM), pp.1974-1983, 2012.

[28] Y.H Kim, “Coding Techniques for Primitive Relay Channels,”45th Annual Allerton Conference on Communication, Control, and Computing,pp.129-135, 2007.

[29] T.M Cover, J.A Thomas. Elements of Information Theory, 2nd ed. New York: Wiley-Interscience,2006.

[30] A. Bravo-Santos, “Polar Codes for the Rayleigh Fading Channel,”IEEE Communications Letters,vol.17, no.12, pp.2352-2355, December 2013.

[31] H.B Si, O.O Koyluoglu, S. Vishwanath, “Polar Coding for Fading Channels: Binary and Exponential Channel Cases,”IEEE Transactions on Communications, vol.62, no.8, pp.2638-2650,August 2014.

[32] L. Liu, C. Ling, “Polar Codes and Polar Lattices for Independent Fading Channels,”IEEE Transactions on Communications, vol.64, no.12,pp.4923-4935, December 2016.

[33] A. Chakrabarti, A. Sabharwal, B. Aazhang, “Low density parity check codes for the relay channel,”IEEE Journal on Selected Areas in Communications, vol.25, no.2, pp.280-291, February 2007.