Efficient Subchannel Allocation Based on Clustered Interference Alignment in Ultra-Dense Femtocell Networks
Hao Zhang , Hongyan Li*, Jung Hoon Lee
1 Department of Telecommunications Engineering, Xidian University, Xi’an 710071, China
2 Department of Electronics Engineering, Hankuk University of Foreign Studies, Yongin 17035, South Korea
* The corresponding author, email: hyli@xidian.edu.cn
I. INTRODUCTION
Femtocell base stations (FBSs) will be mainly expected to extend the indoor coverage and improve the spectrum efficiency for the next generation networks [1]. Due to the dramatic increase in the number of users and their traffic demands [2]-[4], more and more FBSs will be densely deployed over a traditional macrocell network [5]. In this case, neighboring femtocells will introduce severe interference to each other. The interference among femtocell user equipments (FUEs) can be perfectly eliminated by allocating orthogonal subchannels. However, the spectral resources are finite in practical systems, so more efficient interference management schemes are needed in ultra-dense femtocell networks.
Recently, interference alignment (IA) has attracted much attention as a promising interference management scheme especially at high signal-to-noise ratio (SNR) regime [6]. The basic idea of IA is to confine the interference from other transmitters into a reduced subspace, while other dimensions are left to recover the desired signal free from interference[7]. So IA enables multiple users to share the same resources without interference, which improves the spectral efficiency. For K-user interference channel, it was shown that K/2 degrees of freedom (DoF) can be achieved with IA per time, frequency, or space dimension [6]. However, the feasibility condition of IA is determined by the numbers of users, data streams, and antennas equipped in transmitter and receiver [8].
In this paper, the authors proposed a scheme that performs efficient subchannel allocation based on clustered IA in ultra-dense femtocell networks to increases the spectral efficiency.
Clustered IA is mainly proposed to address the feasibility issue of IA by partitioning all users into clusters with each containing smaller number of users, so IA becomes feasible in each cluster. Clustered IA was firstly proposed for cellular networks in [9], and then proposed for ad hoc networks in [10]. The authors of[11] proposed three joint clustering and IA scheduling schemes for overloaded femtocell networks. Nevertheless, these schemes are proposed for TDMA systems, which are not suitable when the users in different clusters transmit data simultaneously. In [12],an interference cost metric was proposed for user clustering. With this metric, strong interference is captured as intra-cluster interference, which can be mitigated by IA in each cluster, and the relatively weak interference is remained as inter-cluster interference and treated as noise. In ultra-dense femtocell networks, however, all of the FBSs and FUEs are much closer to each other, so the inter-cluster interference should not be simply treated as noise. In [13], the authors proposed a cross-tier interference management scheme for multiple-input multiple-output (MIMO)cognitive femtocell networks. In the scheme,the macrocell users sense the environment to find the femtocell base stations (FBSs) which they interfere with, and then design their precoding vectors determined by exploiting IA to suppress the interference they cause at FBSs.To meet the feasibility condition of IA, only the macrocell users which cause strongest interference at each FBS will be selected to perform IA. However, there is no subchannel allocation procedure which leads to the fact that the FBSs suffer from severe interference caused by femtocell users they do not serve in ultra-dense femtocell networks.
Therefore, performing subchannel allocation based on clustered IA is an effective solution to manage the interference in femtocell networks. In [5], the authors exploited IA to mitigate the intra-tier interference,which improves the achievable data rates of femtocell networks. To meet the feasibility condition of IA, the authors also partitioned the femtocell users into several coalitions by coalitional game in partition form. And subcarrier allocation is performed but there are still interferences among different coalitions,which will lead to performance degradation in ultra-dense femtocell networks since the intra-coalition interference is severe. In [14], the authors made a tradeoff between opportunistic resource allocation (ORA) and IA in femtocell networks. To maximize the sum rate, most of the subchannels are allocated to perform ORA in low SNR regime, while at high SNR regime, performing IA will mostly utilize the subchannels. However, the feasibility of IA is not taken into account. The authors of [15] utilized IA with frequency-clustering to improve the spectral efficiency in orthogonal frequency division multiplexing access (OFDMA) based MIMO cognitive radio networks. Nevertheless, the proposed scheme needs to evaluate the achievable sum rate of each possible user combination over each subchannel, which requires global channel state information (CSI).This will result in heavy signaling overhead as well as much higher computational complexity especially in ultra-dense femtocell networks.
In this paper, we investigate the problem of efficient subchannel allocation based on clustered IA (ESCIA) to mitigate the interference in ultra-dense OFDMA based femtocell networks. With the objective of maximizing the achievable sum rate of all FUEs, our problem is formulated as a combinatorial optimization problem. Due to its NP-hardness,we propose a two-phases efficient solution with low-complexity. In the first phase, all the FUEs are grouped into disjoint clusters, each of which contains a limited number of FUEs to meet the feasibility condition of IA. In the second phase, efficient subchannel allocation for the formed clusters performing IA is performed. Furthermore, efficient algorithm with low-complexity is proposed for the corresponding sub-problem in each phase.
The rest of the paper is organized as follows. The system model is presented in Section II. Section III formulates the problem and solve it in two phases by the proposed algorithms. Simulation results are shown in Section IV, and Section V is concluded the paper.
II. SYSTEM MODEL
Our system model is depicted in Fig. 1. All of the FBSs and FUEs are ultra-densely deployed in indoor area, and the downlink case is considered. In such deployment, an FBS will be closer to all the FUEs it does not serve and cause interference to them. Each FBS only serves a single FUE, which was also assumed in [16]. We denote the set of all FUEs and the set of all subchannels byandrespectively, where
In our model, all of the FBSs, FUEs are equipped withMantennas. Moreover, each FBS sendsdata streams to its intended FUE. According to the feasibility condition of IA in [8],andmust meet the following constraint:

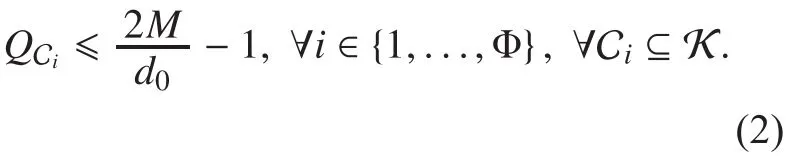
For simplicity, we assume that each cluster contains the same number of FUEs to perform IA and the number of FUEs in each cluster can also achieve the maximum value. In addition,asmust be an integer number, we have
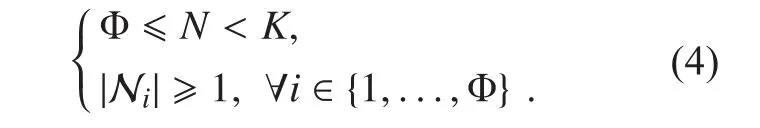
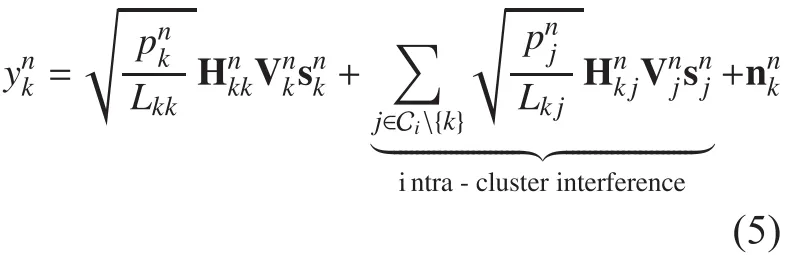
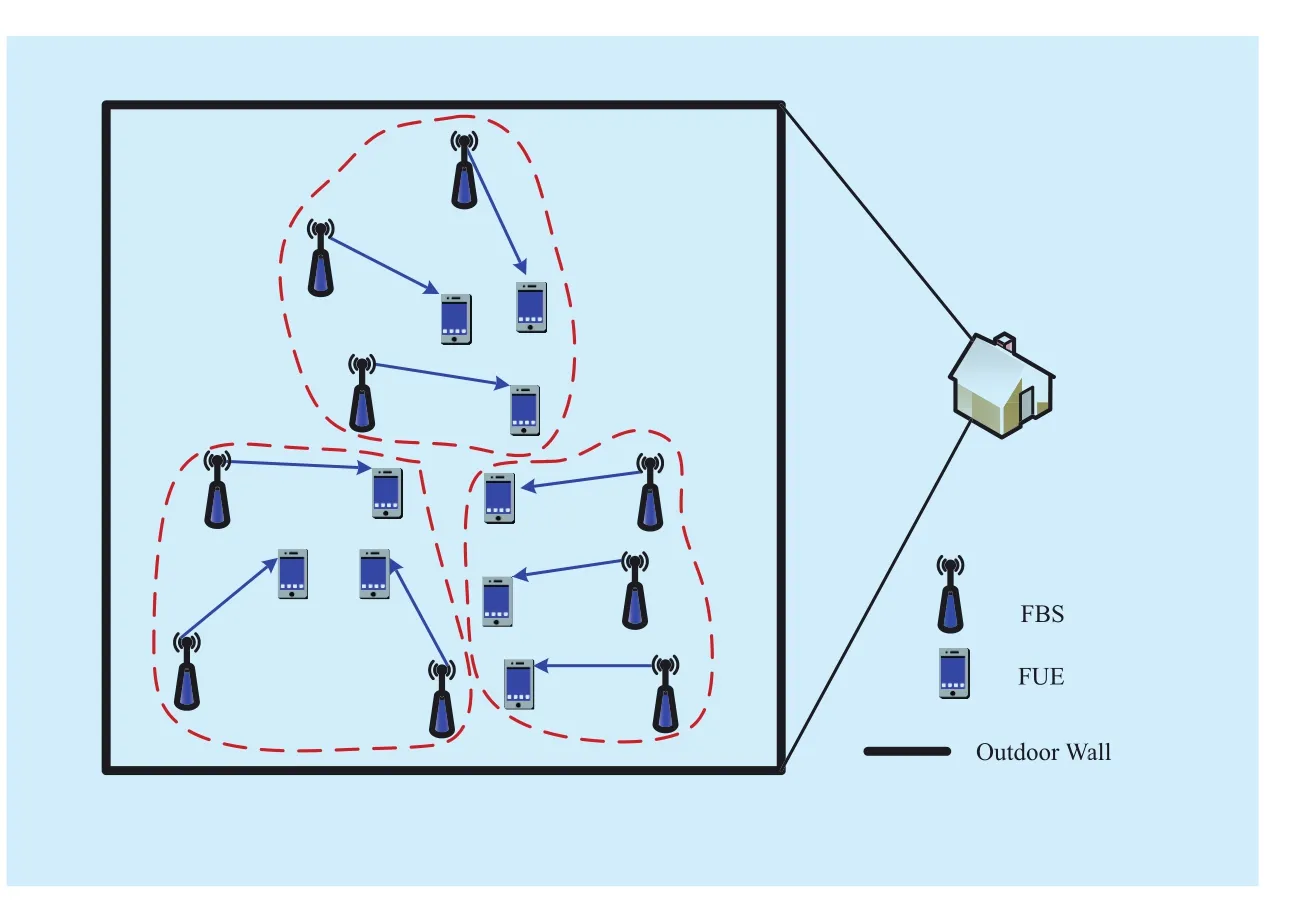
Fig. 1 An example of untra-dense femtocell networks with 9 FUEs in indoor area
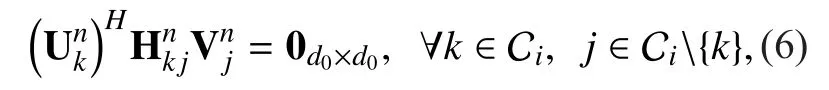
and

where equation (6) indicates that the receive interference suppression matrix must be designed to be orthogonal to the reduced dimensional subspace spanned by all the interference signals at each FUE so that they can be completely eliminated or aligned, and equation (7)makes sure that the desired signals are linearly independent of the subspace spanned by all the interference signals at each FUE so that they will not be zero-forced by each FUE. Also,if equation (6) holds, then equation (7) also holds with the probability of 1 [17]. Thus, we only need to findandthat satisfy equation (6). So the intra-cluster interference can be perfectly eliminated with IA in each cluster.In addition, the inter-cluster interference can be mitigated by subchannel allocation. After postprocessing withthe received signal of FUEkover subchannelnbecomes
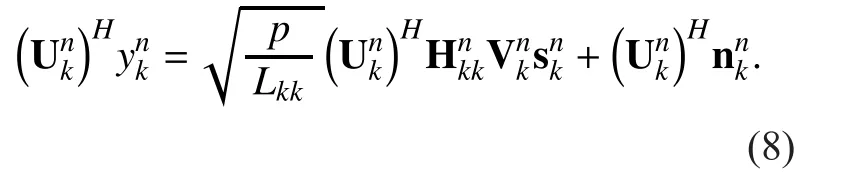
III. PROBLEM FORMULATION AND SUBOPTIMAL ALGORITHMS
3.1 Problem formulation
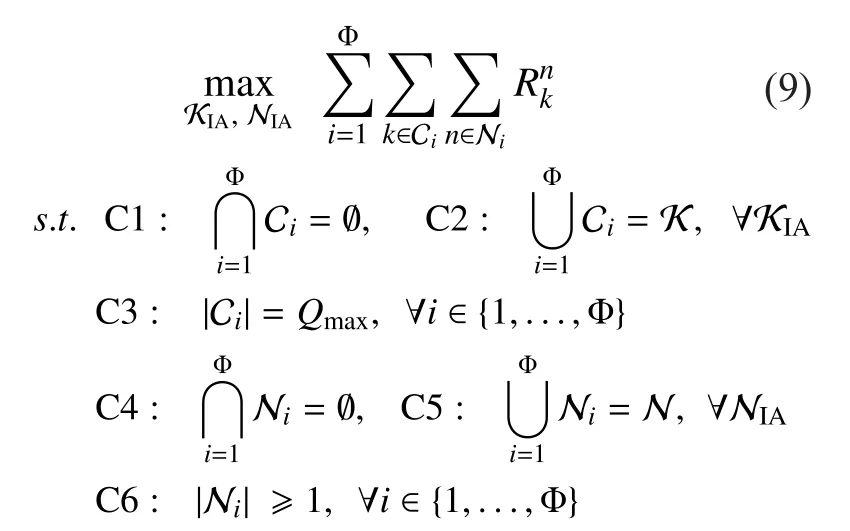

Aspkeeps constant during the whole procedure of subchannel allocation, problem(9) is a combinatorial optimization problem,which is NP-hard. Finding the optimal solution by exhausting all the possible cases will lead to prohibitive computational complexity especially in ultra-dense femtocell networks.Furthermore, exhausting each possible case,i.e., evaluating the achievable data rate of each combination that containsFUEs after performing IA over each subchannel, needs to acquire the accurate global channel state information (CSI), which will result in heavy signaling overhead. As a result, to find an effi-cient solution with low-complexity and reduce the signaling overhead, we propose to solve problem (9) in two phases, i.e., clustering and resource allocation for the formed clusters.The similar method was also used in [16] and[18]. In the first, instead of acquiring the global CSI, we group all the FUEs intoclusters with a relatively rough manner only according to the path losses. By doing this, the signaling overhead is notably reduced. In the second phase, we allocate subchannels to the clusters formed in the first phase. In addition, we propose efficient algorithm with low-complexity to solve the corresponding sub-problem in each phase.
3.2 Proposed solution
3.2.1 Phase 1: clustering
This phase aims at capturing the strong interference as intra-cluster interference so that they can be completely eliminated by clustered IA. To achieve this goal, the approximated rate losswhich was proposed in [12], is used to measure the interference caused by FBSjat
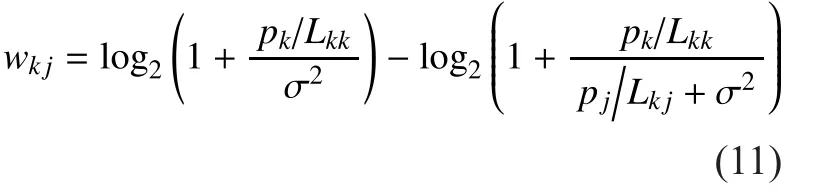
where the first term on the right side of (11)indicates that if FUEkandare in the same cluster (i.e., FBSkandjalso belong to this cluster), so the interference caused by FBSjat FUEkwill be eliminated by clustered IA while only leaving the noise. And the second term on the right side of (11) indicates that if FUEkandjare in different clusters,FBSjwill cause interference to FUEk. Therefore, we use the difference of the two terms to simply measure the approximated rate loss.Intuitively speaking, the largerthe stronger the interference caused by FBSjto FUEkwill be. The metric is only determined by path losses, which can be easily obtained by each FUE through measuring the averaged signal strength of pilot symbols transmitted by other FBSs [12]. Then, without acquiring the accurate global CSI, the signaling overhead will be notably reduced. So the intra-cluster interference in an arbitrary clustercan be approximately measured as:
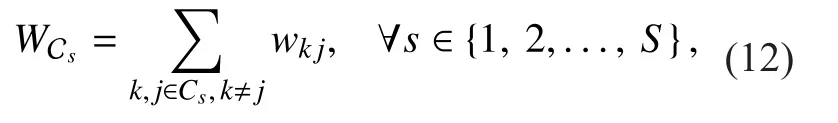
whereSdenotes the number of all cases of selectingFUEs from, i.e,Then, with the objective of capturing relatively strong interference in each cluster, the sub-problem of clustering for FUEs is formulated as
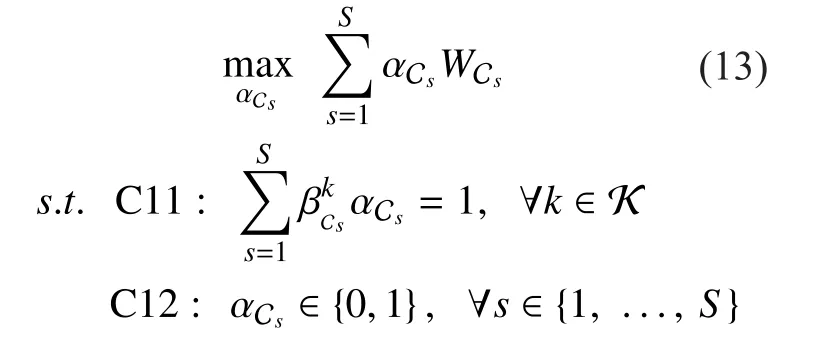
3.2.2 Phase 2: subchannel allocation for clusters
After executing Algorithm 1, the set of FUEsis grouped intoclusters, i.e.,c. Then phase 2 needs to allocate all theNsubchannels to the resultingclusters, i.e.,should be determined.Note that the strong interference is captured as inter-cluster interference in the first phase and will be eliminated by clustered IA. However, in ultra-dense femtocell networks, the inter-cluster interference may be still strong,or some FBSs in clustercause strong inter-cluster interference to FUEs inbut other FBSs incause relatively weak inter-cluster interference to FUEs in. But anyway,clustersandshould be allocated with orthogonal subchannels as long as at least one FBS incause strong inter-cluster interference to at least one FUEs inAs a result,the sub-problem in phase 2 becomes

Algorithm 1 Clustering for FUEs

Algorithm 2 Subchannel Allocation for Clusters

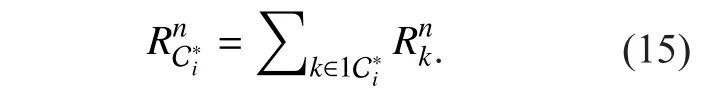
Constraint C21 guarantees that each of theclusters can be allocated with at least one subchannel. C22 ensures that each subchannel can be utilized by only one resulting cluster.C23 indicates that the total number of subchannels allocated toclusters must beN.The above problem is also NP-hard. Therefore,obtaining the optimal solution by exhaustive method will also incur prohibitive computational complexity. As an efficient solution, we first allocate one subchannel to each cluster,and then each of the remainingsubchannels will be allocated to the cluster which achieves the maximum data rate over it. The above two procedures need the accurate CSI in each cluster over each subchannel, which can be estimated by the steps in [5]. More details are shown inAlgorithm 2.
IV. SIMULATION RESULTS
The performance of ESCIA is evaluated in this section. We consider the ultra-dense deployment of femtocells in indoor environment. Both the FBSs and FUEs are uniformly distributed in a square and single-floor apartment with an edge of 10 m. The apartment is separated into different rooms by inner walls.The system parameters, which are unchanged during the simulations, are listed in Table 1.Both path loss and shadowing are considered in the simulation. Here the path loss from each FBS to its intended FUE and other FUEs can be found in the indoor femtocell channel models (urban deployment) of [22]. All the FBSs and FUEs are assumed to have 4 antennas. In addition, each FBS sends 2 data streams to its intended FUE. Therefore, according to the feasibility condition of IA in [3], we haveQmax=3.We also assume that the transmit power of each FBS over each subchannel is also the same, i.e.,
In our simulations, the performance of following schemes are evaluated.
1)Optimal solution: exhausting all the possible cases of clustering and subchannel allocation to obtain the optimal solution to problem (9).
2)ESCIA: proposed scheme.
3)Subchannel allocation by BnB: usingAlgorithm 1for clusteringand BnB algorithm to solve the sub-problem of subchannel allocation in phase 2.
4)Method in [12]:using the method in[12] to solve the sub-problem of clustering for FUEs in phase 1andAlgorithm 2for subchannel allocation in phase 2.
5)Random clustering: randomly selecting FUEs to form clusters and usingAlgorithm 2for subchannel allocation.
6) Scheme with no clustering: allocating one orthogonal subchannel to each of theNFUEs selected from.
Fig. 2 shows the achievable sum rate of all FUEs with respect to the transmit power of each FBS over each subchannelp. We haveK=12 andN=6. So all the 12 FUEs are grouped into 4 clusters. For all the six schemes, the achievable sum rates of all FUEs increase as the transmit power of FBSs increases. Scheme with no clustering shows the worst performance since only 6 FUEs, which are selected from, are eligible to be allocated with one orthogonal subchannel over which they can achieve the maximum data rate. By exploiting IA to increase the spectral efficiency as well as eliminate the intra-cluster interference, theFUEs in each cluster can share subchannels without any intra-cluster interference. So all the 12 FBSs can send 2 data streams to their intended FUEs. This is why the performance gaps between scheme with no clustering and five clustered IA schemes become larger aspincreases. Paying no attention to the effect of path losses on forming clusters, scheme of random clustering does not show good performance compared with ESCIA and other two clustered IA schemes. It can be also observed that ESCIA achieves almost the same performance as that of subchannel allocation by BnB whose computational complexity is the same as that of exhaustive search in the worst case [16]. Furthermore, the performance of ESCIA is closer to that of the optimal solution aspincreases, which verifies the effectiveness of the proposed solution.

Table I Parameters
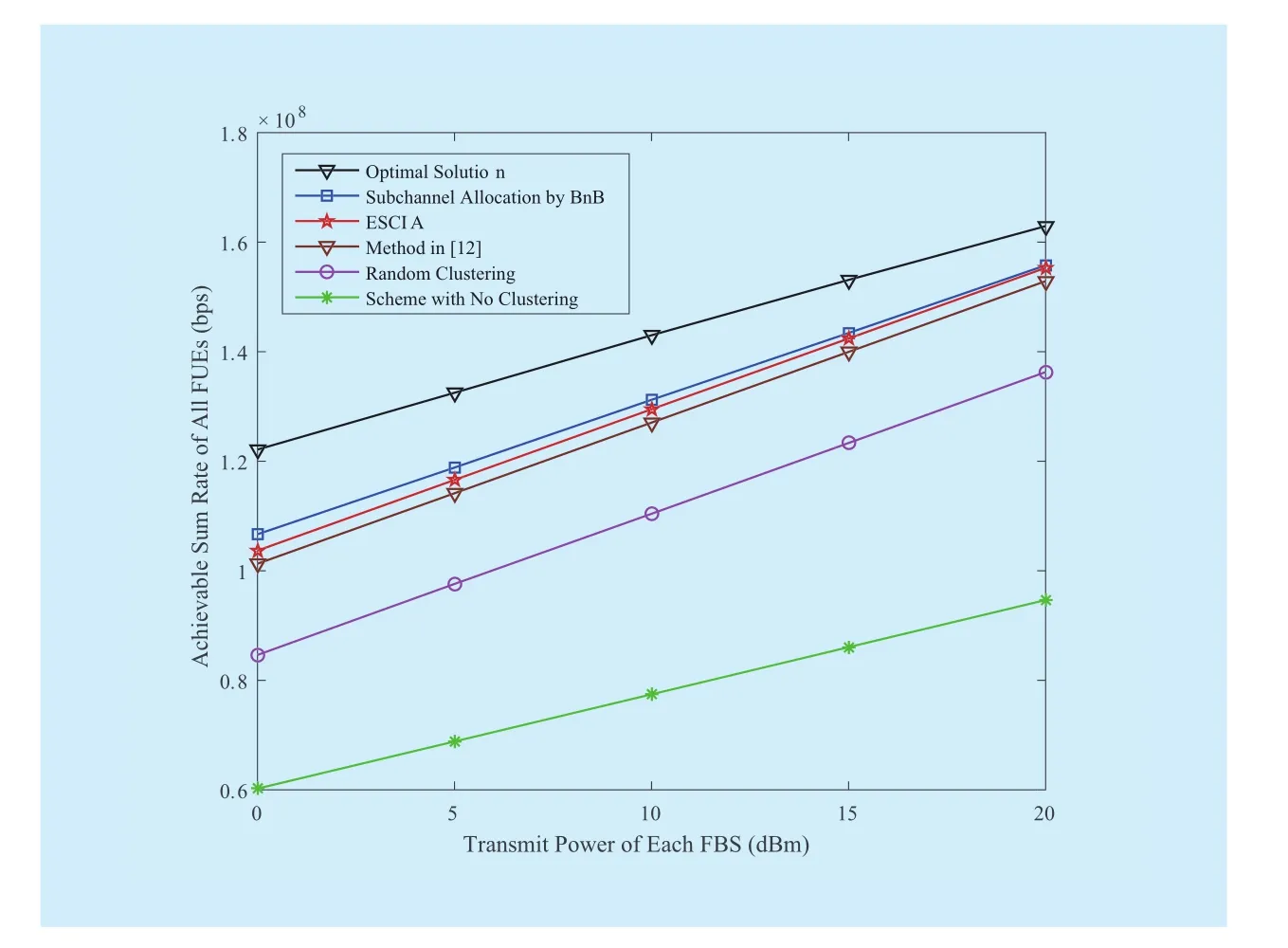
Fig. 2 Achievable sum rate vs. transmit power of each FBS
Fig. 3 shows the achievable sum rate of all FUEs with respect to the number of FUEsK.We have We havep=30 mW andN=10. AsKincreases, it will result in unaffordable computational complexity if we use exhaustive search to obtain the optimal solution to problem (9). Therefore, as an approximation of the optimal solution, we use Algorithm 1 for suboptimal clustering and exhaustive search for the optimal subchannel allocation (SC+OSA). We can observe that the scheme with no clustering has the worst performance which is hardly improved asKincreases. This is because only 10 FUEs are selected to be allocated with one subchannel each regardless of the increase inK. Nevertheless, the performances of the other 4 clustered IA schemes linearly increase withK, which demonstrates that IA can notably improve the spectral efficiency, and it is also much more beneficial to performing clustered IA in ultra-dense femtocell networks.
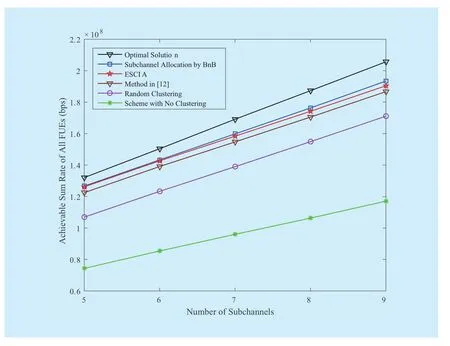
Fig. 4 Achievable sum rate vs. the number of subchannels
Fig. 4 illustrates the achievable sum rate of all FUEs with respect to the number of subchannels availableN. We haveK=12 andp=30mW(14.77dBm). In the scheme with no clustering, asNincrease, more and more FUEs are eligible to be allocated with orthogonal subchannels. But the five clustered IA schemes still exhibits much better performance, which implies that the scheme with no clustering has a much lower spectral efficiency. It is worth mentioning that the performance gap between ESCIA and optimal solution gets a little larger asNincrease, but ESCIA has a much lower computational complexity.
V. CONCLUSIONS
In this paper, we proposed a scheme that performs efficient subchannel allocation based on clustered IA in ultra-dense femtocell networks, which mitigates both intra-cluster and inter-cluster interferences, and notably increases the spectral efficiency. The problem is formulated as a combinatorial optimization problem, which is known as NP-hard. To obtain an efficient solution, we propose to solve the problem in two phases. In the first phase,the FUEs are grouped into disjoint clusters,each of which contains limited number of FUEs to meet the feasibility condition of IA.In the second phase, subchannel allocation for the formed clusters where IA is exploited is performed. Furthermore, an algorithm with low-complexity is proposed for each of the sub-problems in the two phases. Simulation results demonstrate that ESCIA not only exhibits better performance than other related schemes but also achieves almost the same performance as the BnB algorithm. Moreover,the performance of ESCIA is close to the optimal solution, which verifies the effectiveness of our proposed solution.
ACKNOWLEDGEMENTS
This work was partially supported by China Scholarship Council (201406960042);the National Science Foundation(91338115,61231008); National S&T Major Project (2015ZX03002006); Program for Changjiang Scholars and Innovative Research Team in University (IRT0852), and the 111 Project (B08038).
[1] V. Chandrasekhar, J. G. Andrews, and A. Gatherer, “Femtocell networks: a survey,”IEEE Communications Magazine, vol. 46, no. 9, pp. 59-67,Sep. 2008.
[2] X. D. Pang, W. Hong, T. Y. Yang, and L. S. Li,“Design and implementation of an active multibeam antenna system with 64 RF channels and 256 antenna elements for massive MIMO application in 5G wireless communications,”China Communications, vol. 11, no. 11, pp. 16-23, Nov. 2014.
[3] S. Z. Chen, S. H. Sun, Y. M. Wang, G. J. Xiao, and R. Tamrakar, “A comprehensive survey of TDD-based mobile communication systems from TD-SCDMA 3G to TD-LTE 4G and 5G directions,”China Communications, vol. 12, no. 2, pp. 40-60, Feb. 2015.
[4] L. Huang, Y. Q. Zhou, Y. Y. Wang, X. Han, J. L. Shi,and X. X. Chen, “Advanced coverage optimization techniques for small cell clusters,” China Communications, vol. 12, no. 8, pp. 111-122,Aug. 2015.
[5] F. Pantisano, M. Bennis, W. Saad, M. Debbah,and M. Latva-aho, “Interference alignment for cooperative femtocell networks: a game-theoretic approach,”IEEE Transactions on Mobile Computing, vol. 12, no. 11, pp. 2233-2246, Nov.2013.
[6] V. R. Cadambe and S. A. Jafar, “Interference alignment and degrees of freedom of the k-user interference channel,”IEEE Transactions on Information Theory, vol. 54, no. 8, pp. 3425-3441, Aug. 2008.
[7] S. A. Jafar, “Interference alignment: a new look at signal dimensions in A communication network,” Foundations and Trends in Communications and Information Theory, vol. 7, no. 1, pp.1-136, Jun. 2011.
[8] C. Yetis, T. Gou, S. A. Jafar, and A. Kayran, “On Feasibility of Interference Alignment in MIMO Interference Networks.IEEE Transactions on Signal Processing, vol. 58, no. 9, pp. 4771-4782,Sep. 2010.
[9] R. Tresch and M. Guillaud, “Clustered interference alignment in large cellular networks,” IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, pp. 1024-1028, Sep. 2009.
[10] R. Tresch and M. Guillaud, “Performance of interference alignment in clustered wireless ad hoc networks,” IEEE International Symposium on Information Theory, pp. 1703-1707, Jun. 2010.
[11] S. B. Halima and A. Saadani, “Joint clustering and interference alignment for overloaded femtocell networks,”IEEE Wireless Communications and Networking Conference, pp.1229-1233, Apr.2012.
[12] S. J. Chen and R. S. Cheng, “Clustering for interference Alignment in multiuser interference network,”IEEE Transactions on Vehicular Technology, vol. 63, no. 6, pp. 2613-2624, Jul. 2014.
[13] B. Guler, A. Yener, “Selective interference alignment for MIMO cognitive femtocell networks”.IEEE Journal on Selected Areas in Communications, vol. 32, no. 3, pp. 439-450, Mar. 2014.
[14] N. Lertwiram, P. Popovski, and K. Sakaguchi,“A study of trade-off between opportunistic resource allocation and interference alignment in femtocell scenarios,” IEEE Wireless Communications Letters, vol. 1, no. 4, pp. 356-359, Aug.2012.
[15] M. El-Absi, M. Shaat, F. Bader, and T. Kaiser, “Interference alignment with frequency-clustering for efficient resource allocation in cognitive radio networks,”IEEE Global Telecommunications Conference, pp. 979-985, Dec. 2014.
[16] A. Abdelnasser, E. Hossain, and D. I. Kim, “Clustering and resource allocation for dense femtocells in a two-tier cellular OFDMA network,”IEEE Transactions on Wireless Communications,vol.13, no. 3, pp. 1628-1641, Mar. 2014.
[17] K. Gomadam, V. Cadambe, and S. A. Jafar, “A distributed numerical approach to interference alignment and applications to wireless interference networks,”IEEE Transactions on Information Theory, vol. 57, no. 6, pp. 3309-3322, Jun.2011.
[18] K. Hosseini, H. Dahrouj, and R. Adve, “Distributed clustering and interference management in two-tier networks,”IEEE Global Telecommunications Conference, pp. 4267-4272, Dec. 2012.
[19] J. C. Fan, G. Y. Li, Q. Y. Yin, B. G. Peng, and X. L.Zhu, “Joint User Pairing and Resource Allocation for LTE Uplink Transmissions,”IEEETransactions on Wireless Communications, vol. 11, no. 8, pp.2838-2847, Aug. 2012.
[20] S. Sakai, M. Togasaki, and K. Yamazaki, “A note on greedy algorithms for the maximum weighted independent set problem,”Discrete Applied Mathematics, vol. 126, no. 2-3, pp. 313-322,Mar. 2003.
[21] K. W. Choi, E. Hossain, and D. I. Kim, “Downlink subchannel and power allocation in multi-cell OFDMA cognitive radio networks,”IEEE Transactions on Wireless Communications, vol. 10, no.7, pp. 2259-2271, Jul. 2011.
[22] 3rd Generation Partnership Project (3GPP),“Further advancements for E-UTRA physical layer aspects (Release 9),” TR 36.814, 3GPP, Mar.2010.
- China Communications的其它文章
- X-Band Power Amplifier for Next Generation Networks Based on MESFET
- A VMIMO-Based Cooperative Routing Algorithm for Maximizing Network Lifetime
- Efficient Packet Scheduling Technique for Data Merging in Wireless Sensor Networks
- Energy Estimation and Optimization Platform for 4G and the Future Base Station System Early-Stage Design
- A Novel Forwarding Method for Full-Duplex Two-Way Relay Networks
- Versatile Routing and Self-Certifying Features Support for Secure Mobility in eXpressive Internet Architecture

