A Novel Forwarding Method for Full-Duplex Two-Way Relay Networks

Shuangshuang Han, Xiang Cheng, Liuqing Yang

1 The State Key Laboratory of Management and Control for Complex Systems, Institute of Automation, Chinese Academy of Sciences,Beijing, China and Qingdao Academy of Intelligent Industries, Qingdao, China

2 The State Key Laboratory of Advanced Optical Communication Systems and Networks, School of Electronics Engineering and Computer Science, Peking University, Beijing, China

3 Department of Electrical and Computer Engineering, Colorado State University, Fort Collins, CO 80523 USA

I. INTRODUCTION

Full-duplex transmission has attracted a great number of attention in recent years, which is also an important optional technique for 5G wireless communication systems[1]-[3].Full-duplex relay techniques can achieve higher link capacity and obtain lower end-to-end latency[4]. Further, in order to improve spectral efficiency over one-way relay networks,two-way relay network was firstly exploited by Shannon [5] and now has drawn much attention [6]-[11] due to its potential application to enable range-rate enhancements to future cellular systems. The overall communication rate between two source terminals is approximately twice of that achieved in one-way relay networks, which makes a two-way relay network particularly attractive to bidirectional systems[12]-[14].

Relay strategies have thus been studied in[15]-[18]. An amplify-and-forward (AF) relay amplifies its received signals and retransmits to the receivers. This simple processing enables full spatial diversity at high signal-tonoise ratios (SNRs) [19]. However, AF also enhances the noise component, it results in degraded performance (measured by symbol error rate (SER)). On the other hand, a decode/detect-and-forward (DF) relay first decodes or detects the source signal and then forwards the regenerated signals to the receivers. However,when the source-relay link suffers from deep fading (low SNRs), the decoding errors at the relay propagate to the destination.

The authors proposed an estimate-and-forward (EF) relay strategy to improve the error performance for SISO and MIMO full-duplex two-way relay networks in this paper.

Another relay strategy, estimate-and-forward(EF) [20], is a powerful approach for uncoded single antenna one-way relay networks. Unlike the AF and DF relays, the EF relay computes and transmits an unconstrained minimum mean squared error (MMSE) estimate, resulting an optimized relay function for all SNRs.

This paper investigates EF relay strategy for SISO and MIMO full-duplex two-way relay networks.

Main Contributions are summarized as follows:

1) An EF relay for full-duplex two-way relay networks is developed, which forwards a scaled version of an unconstrained MMSE estimate of the received signal at the relay.The scaling factor is chosen to satisfy the relay average power constraint. Unlike AF and DF, the proposed EF works equally well for both low and high SNRs, and outperforms these two schemes.

2) we theoretically analyze and prove the convergence of EF to AF and DF for two-way relay networks with arbitrary number of antennas. Thus, in low and high SNR regions,the EF converges to AF and DF, respectively.

3) To reduce the complexity for the systems with high order constellations and/or a large number of antennas (large MIMO)[21],[22],a list EF relay is developed, which computes the MMSE estimate by using a sphere decoder to generate a list of candidate vectors. A 2×2 4-QAM MIMO relay system is discussed in Section IV.

Fig. 1 A full-duplex two-way relay system model

4) The generalized sphere decoder is applied by the relay node in both DF and list EF cases. In DF, the generalized sphere decoder is used to detect the transmitted signal because it is an under-determined MIMO detection problem at the relay. Similarly, for list EF case, it is used to generate the candidate list for MMSE estimate at the relay.

The rest of this paper is organized as follows. Section II introduces the system model of a full-duplex two-way relay networks and conventional forwarding methods, where all the terminals and the relay have multiple antennas. In Section III, the EF relaying strategy for MIMO full-duplex two-way relay networks is proposed, and an approximate list EF is also developed and analyzed. Simulation results and discussions for SISO and MIMO full-duplex two-way relay networks are given in Section IV. Finally, conclusions are drawn in Section V.

II. SYSTEM MODEL

2.1 System model

A full-duplex two-way relay network is illustrated in Fig. 1, where the first terminal nodehasantennas, the relayhasreceive antennas andtransmit antennas, and second terminal nodehasantennas. For simplicity, we assume only one relayin the full-duplex two-way relay network and terminalsandexchange information via the relay.

In the first time slot, the two terminalsandsend the transmitted signalsandto the relay. The relay receives the signal fromand itself, which is given as

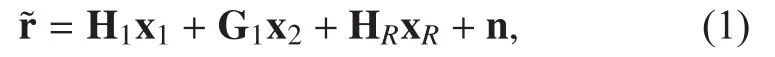
In the second time slot, the relay receives the signals fromandand generates and transmits the processed signal to the opposite terminal. In this paper, we assume that the relay node has full knowledge of the loop interference channel and the transmitted signal by itself; thus, the signal from the loop channel can be perfectly removed. Therefore, the received signal would be derived as

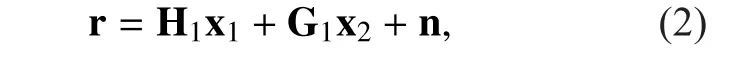
Throughout this paper, we assume the channel state information is available at the relay and the two terminal nodes. Furthermore,we assume that there is only one relay in this full-duplex two-way relay network for simplicity. But the extension to include multiple relays is straightforward but omitted due to space limitation.

2.2 Conventional forward strategies

The performance of relay networks depends critically on the relay function. Several relay functions of memoryless forwarding strategies are discussed here. We takeas the destination for an example, and then similar process could be implemented for terminal

1) Amplify-and-forward:Within the classical relay strategies, AF relaying is the most basic relay strategy. For each transmit symbol, the relay retransmits a scaled version of the received signal. Thus, a linear relay function is used.Furthermore, to satisfy the average power constraint, the AF relay function can be given as

Due to its low complexity and easy implementation, the AF relaying is one of the most attractive cooperative diversity schemes for relay networks. No detection process at the relay facilitates the use of simple relay units. However, the main disadvantage is the performance loss due to the noise amplification at the relay.

2) Decode-and-forward:DF relay has attracted much attention recently because it outperforms AF in the high SNR region. It detects data from the incoming signal, remodulates and forwards the processed signal to the destination. It may use an ML decoder for detection of data from the incoming signal. The detected signal vector may be given as

Note that Eq. (6) represents an under-determined MIMO detection, where the number of the unknowns is more than the number of equations. The generalized sphere decoder for rank-deficient MIMO systems can be employed to perform (6) here. While can be directly transmitted tothe relay power constraints must be satisfied. Therefore, the DF relay function can be given as

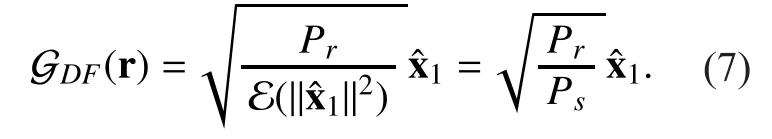
III. ESTIMATE AND FORWARD

3.1 Estimate-and-forward

In this paper, EF relay is developed for full-duplex two-way relay networks, which achieves the advantages of AF and DF for all SNRs without switching between algorithms(AF and DF).

The main idea is described here. Unlike DF and AF, the EF relay transmits a soft information with uncertainty to the receiver. The soft information is generated by scaling the unconstrained MMSE solution of the received signal at. Assuming equal priori probabilities for all transmitted symbols, the MMSE estimate of the received signalat the relay can be given as

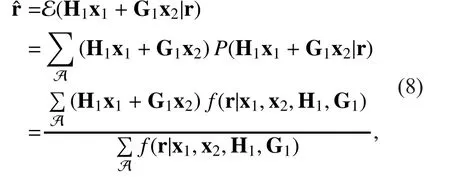
Therefore, Eq. (8) can be computed as

As with AF and DF relaying, to satisfy the relay power constraint, the scaling factor is given by

By using the total probability law, the PDF of the received signalcan be derived as

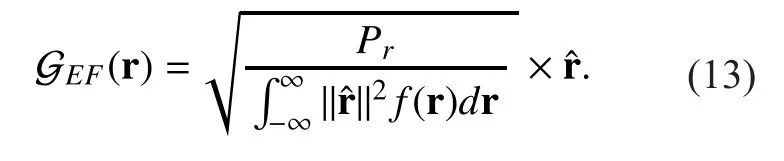
3.2 Analysis of EF performance

In this subsection, we show theoretically that EF approximates AF and DF in low SNR and high SNR regions. We assume that the constellation is symmetric, i.e.,For simplification, we definein this section.

Low SNR Case:When the receive SNR at the relay is low, by using Eq. (8), the MMSE estimate can be derived as Eq. (14). Because of the fact that the constellation is symmetric and thusis an even function inthe above equality could be derived as

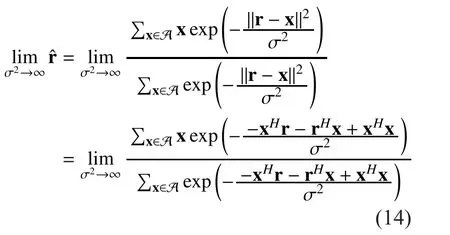
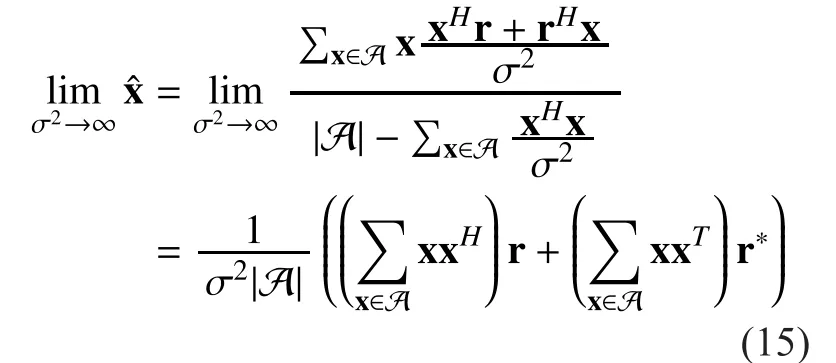
From Eq. (15), we see that EF converges to AF in the low SNR region, but in a slightly different from the pure AF. This can be further simplified for different constellations.

High SNR Case:We assume the ML detection isfor high SNR, by splitting out the ML solution, the MMSE estimate can be derived as Eq. (16)shown in the bottom at this page. whereFor allwe havethemust be great thanIn other words, it is lower bounded bywith probability one as SNR goes to infinity. Therefore, we have

The MMSE estimate thus approximates to be

which is in fact DF relaying. Consequently, in the high SNR region, EF converges to DF.

3.3 List estimate-and-forward

For large MIMO systems, most of the terms in the sum of Eq. (10) are small and contribute very little to the sum, especially in the high SNRs. Intuitively, one can find a subset ofto compute the sum in Eq. (10).Assume that this subset can be denoted by,and then we can approximate (10) to be

In this paper, we use the size of the listto obtain the trade-offs between the computational accuracy and complexity. Thus,is small,is computed with low complexity. In the high SNR region, because of the limit of exponential functionwe can derive

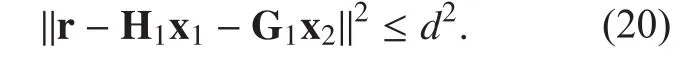
Eq. (20) represents an under-determined MIMO sphere detection problem, which can be solved by the generalized sphere decoder.

Fig. 2 Error performance of relay strategies in a single antenna full-duplex twoway relay network (16-QAM)

Fig. 3 Error performance of relay strategies in a 2×2 full-duplex two-way relay network (16-QAM)

IV. SIMULATION RESULTS

In this section, the performance measured by SER for different strategies (the proposed list EF, EF, DF, and AF) are compared in SISO and MIMO full-duplex two-way relay networks, where the power at the source and the relay are equaland noise varianceAt the second terminal, the received signal (3) is decoded by using the sphere decoder. We choose the list sizeof the proposed list EF to be 4.

First, the SER performance for a SISO full-duplex two-way relay system with a 16 QAM is given in Fig. 2, which compares the proposed EF relays with the classical relays(AF and DF) for different SNRs. As expected,both list EF and exact EF achieve performance gains over DF and AF. For example, at anof 10-3, the proposed exact EF gains 2 dB and 3 dB over the DF and AF relay, respectively.Furthermore, according to Section III-A, exact EF needs to compute all the 162=256 terms inwhile list EF only computes 4 terms according to Eq. (18) in Section III-C. Nevertheless, list EF performs approximately the same to exact EF over all SNRs. Therefore, although list EF generates only an approximate MMSE estimate, its performance is excellent and computational complexity is low. Another interesting observation is that AF outperforms DF in the low SNR region, while it performs worse than DF in the high SNR region. However, the proposed two EF strategies obtain the optimized performance for all SNRs without switching between algorithms.

In order to evaluate the benefits of the proposed EF relay for MIMO full-duplex twoway relay networks. The SER performance of different relay strategies for a 2×2 16-QAM relay network is given in Fig. 3. The two proposed EF relay schemes are compared with the classical DF and AF schemes. From Section III-C, exact EF needs to compute all the 162+2=65536 terms. In contrast, list EF (4 terms ) significantly reduces the computational complexity. Note that EF outperforms DF and AF strategies. For example, at anof 10-3,it gains 1.5 dB and 3 dB over DF and AF, respectively. Furthermore, with a small list sizelist EF approaches the performance of the exact EF case withwith negligible performance loss.

V. CONCLUSIONS

For SISO and MIMO full-duplex two-way relay networks, this paper proposed an estimate-and-forward (EF) relay strategy to improve the error performance. It was shown that this relay strategy outperforms AF and DF across all SNRs, which overcome the disadvantages of the latter two schemes. Furthermore,for a MIMO full-duplex two-way relay network with a large number of antennas and/or high order constellations, List EF relay was also proposed to reduce the computational complexity. It uses the generalized sphere decoder for generating the reduced candidate list. Thus, the computational complexity is reduced especially for large MIMO full-duplex or half-duplex two-way relay networks, while still achieving almost the same performance as the exact EF relay. Consequently, it offers a flexible trade-off between the performance and the complexity by choosing different size of the candidate list.The simulation results confirm the performance gain of the proposed exact EF and list EF over AF and DF relay cases.

ACKNOWLEDGEMENT

This work was supported in part by the National Natural Science Foundation of China 61501461, 61471269, 61622101 and 61571020; the National 973 Project under grant 2013CB336700, the National 863 Project under grant SS2015AA011306, the National Science Foundation under grant number CNS-1343189 and ECCS-1232305, and the Early Career Development Award of SKLMCCS (Y3S9021F34).

[1] Z. Zhang, K. Long, A. V. Vasilakos, and L. Hanzo, “Full-duplex wireless communications:Challenges, solutions, and future research directions,”IEEE Proceedings, vol. 104, no. 7, pp.1369–1409, Jul. 2016.

[2] A. Sabharwal, P. Schniter, D. Guo, D. W. Bliss, S.Rangarajan, and R. Wichman, “In-band full-duplex wireless: Challenges and opportuni- ties,”IEEE J. Sel. Areas Commun., vol. 32, no. 9, pp.1637–1652, Sep. 2014.

[3] D. Kim, H. Lee, and D. Hong, “A survey of inband full-duplex transmission: From the perspective of PHY and MAC layers,”IEEE Commun.Surveys Tutorials, vol. 17, no. 4, pp. 2017–2046,Fourthquarter 2015.

[4] Z. Zhang, X. Chai, K. Long, A. V. Vasilakos, and L.Hanzo, “Full duplex techniques for 5G networks:self-interference cancellation, protocol design,and relay selection,”IEEE Commun. Mag., vol.53, no. 5, pp. 128–137, May 2015.

[5] C. E. Shannon, “Two-way communication channels,” inProc. 4th Berkeley Symp. on Math. Statist. and Prob., vol. 1, 1961, pp. 611–644.

[6] F. Gao, T. Cui, and A. Nallanathan, “On channel estimation and optimal training design for amplify and forward relay networks,”IEEE Trans.Wireless Commun., vol. 7, no. 5, pp. 1907–1916,May 2008.

[7] S. Bagheri, F. Verde, D. Darsena, and A. Scaglione, “Randomized decode-and-forward strategies for two-way relay networks,”IEEE Trans.Wireless Commun., vol. 10, no. 12, pp. 4214–4225, Dec. 2011.

[8] R. Vaze and R. Heath, “On the capacity and diversity-multiplexing tradeoff of the two-way relay channel,”IEEE Trans. Inf. Theory, vol. 57,no. 7, pp. 4219 –4234, Jul. 2011.

[9] B. Zhong and Z. Zhang, “Opportunistic two-way full-duplex relay selection in underlay cognitive networks,”IEEE Systems Journal, vol. PP, no. 99,pp. 1–10, 2016.

[10] J. Wang, F. Shu, R.-q. Chen, Y.-d. Cui, Y. Chen,and J. Li, “Adaptive robust beamformer formulti-pair two-way relay networks with imperfect channel state information,”Frontiers of Information Technology & Electronic Engineering,vol. 17, no. 3, pp. 265–280, 2016. [Online]. Available: http://dx.doi.org/10.1631/FITEE.1500134

[11] Z. Zhang, Z. Ma, Z. Ding, M. Xiao, and G. Karagiannidis, “Full-duplex two-way and one-way relaying: Average rate, outage probability and tradeoffs,”IEEE Trans. Wireless Commun., vol. PP,no. 99, pp. 1–1, 2016.

[12] Q. You, Z. Chen, and Y. Li, “A multihop transmission scheme with detect-and-forward protocol and network coding in two-way relay fading channels,”IEEE Trans. Veh. Technol., vol. 61, no. 1, pp. 433–438, Jan. 2012.

[13] F. Gao, R. Zhang, and Y. C. Liang, “Optimal channel estimation and training design for twoway relay networks,”IEEE Trans. Commun., vol.57, no. 10, pp. 3024–3033, Oct. 2009.

[14] T. Cui, F. Gao, T. Ho, and A. Nallanathan, “Distributed space time coding for two-way wireless relay networks,”IEEE Trans. Signal Process., vol.57, no. 2, pp. 658 –671, Feb. 2009.

[15] Y. Zou, J. Zhu, X. Wang, and V. Leung, “Improving physical-layer security in wireless communications using diversity techniques,”IEEE Network,vol. 29, no. 1, pp. 42–48, Jan. 2015.

[16] Y. Jing and B. Hassibi, “Distributed space-time coding in wireless relay networks,”IEEE Trans.Wireless Commun., vol. 5, no. 12, pp. 3524–3536, Dec. 2006.

[17] G. Liu, F. Yu, H. Ji, V. Leung, and X. Li, “In-band full-duplex relaying: A survey, research issues and challenges,”IEEE Communications Surveys Tutorials, vol. 17, no. 2, pp. 500–524, Secondquarter 2015.

[18] J. Wang, F. Shu, X. Huang, and Y. Wang, “Optimal coherent combining scheme for relay networks,”Wireless Personal Communications, vol.88, no. 3, pp. 575–585, 2016. [Online]. Available:http: //dx.doi.org/10.1007/s11277-016-3179-y

[19] J. Laneman, D. Tse, and G. Wornell, “Cooperative diversity in wireless networks: Efficient protocols and outage behavior,”IEEE Trans. Inf. Theory, vol. 50, no. 12, pp. 3062 – 3080, Dec. 2004.

[20] K. S. Gomadam and S. A. Jafar, “Optimal relay functionality for SNR maximization in memoryless relay networks,”IEEE J. Sel. Areas Commun.,vol. 25, no. 2, pp. 390 –401, Feb. 2007.

[21] Z. Zhang, X. Wang, K. Long, A. Vasilakos, and L. Hanzo, “Large-scale MIMO-based wireless backhaul in 5G networks,”IEEE Wireless Commun., vol. 22, no. 5, pp. 58–66, Oct. 2015.

[22] S. Yang and L. Hanzo, “Fifty years of MIMO detection: The road to large-scale MIMOs,”IEEE Communications Surveys Tutorials, vol. 17, no.4, pp. 1941–1988, Fourthquarter 2015.

[23] O. Damen, A. Chkeif, and J.-C. Belfiore, “Lattice code decoder for space-time codes,”IEEE Commun. Lett., vol. 4, no. 5, pp. 161–163, May 2000.