Algebraic-Based Nonbinary LDPC Codes with Flexible Field Orders and Code Rates

Hengzhou Xu , Dan Feng , Cheng Sun , Baoming Bai ＊

1 State Key Laboratory of Integrated Service Networks, Xidian University, Xi’an 710071, China

2 Science and Technology on Communication Networks Laboratory, Shijiazhuang 050081, China

* The corresponding author, email: bmbai@mail.xidian.edu.cn.

I. INTRODUCTION

Nonbinary low-density parity-check (LDPC)codes, which were proposed based on modular arithmetic by Gallager [1] and redefined over finite fields by Davey and MacKay, have been shown that they can outperform their binary counterpart at the cost of much higher decoding complexity [2]. Therefore, reducing the decoding complexity without sacrificing performance (or with slight performance loss)attracts much research effort [3–6].

Another focal point of research is the construction of nonbinary LDPC codes. Like binary LDPC codes [7–10], the construction methods for nonbinary LDPC codes can be divided into two major classes: random-like constructions by means of computer search[11–12] and algebraic constructions based on finite fields [13], finite geometries [14],graph theory [15], and combinatorial designs[16]. Algebraic-based LDPC codes have advantages of easy hardware implementation of encoding and decoding, fast convergence of iterative decoding, and low error-floor [17].Furthermore, it is easy and simple to construct algebraic-based LDPC codes with large minimum distances which is extremely important for these codes to have good error performance (especially in the error-floor region).Moreover, research results [18] show that the performance of an LDPC code when decoded with the iterative algorithms can be improved efficiently as row redundancies of its parity-check matrix increase. Generally, nonbinary LDPC codes with large row redundancies are constructed based on finite fields [13], finite geometries [14], and dispersed Reed-Solomon codes [19]. But the field order of these codes will be fixed after the base matrices used in the code construction are determined. That is, the transformation of the field order is not flexible.

The authors analyzed the rank of matrices over, and proposed two methods for constructing algebraic- based nonbinary LDPC codes.

In this paper, we mainly focus on the construction of nonbinary LDPC codes whose parity-check matrices have row redundancies.The proposed codes can be defined in any field and have various rates for a given field. We first analyze the rank of matrices overand propose an algebraic-based method for constructing LDPC codes over arbitrary finite fields. A family of nonbinary LDPC codes over different finite fields with the same degree distribution, dimension, and block length(in symbols) is then obtained, where the code length in bits varies with field size. Note that the resulting codes can be viewed ascolumn-scaledLDPC (CS-LDPC) codes in [20],but we generalize its construction method. By replacing 1’s in one column (or more columns)of the associated binary parity-check matrix of an original LDPC code with different nonzero elements ofanother family of LDPC codes overwith various rates can be also constructed. Simulation results show that the proposed codes have good performance over the BPSK modulated AWGN channel and fast iterative decoding convergence.

II. STUCTURAL PROPERTIES OF MATRICES OVER FINITE FIELDS

2.1 Finite fields

In this paper, we are concerned with finite fields of characteristic 2. It is well known that[21] the Galois (or finite) fieldcan be constructed based on a special irreducible polynomial:

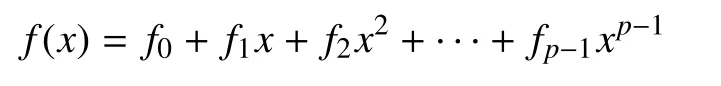
withpbeing any positive integer, which is referred to as primitive polynomial. A nonzero elementis called a primitive element ofif it is a root ofThe powers ofform all elements of. Another representation of elements in finite fieldis polynomial. For any elementit also can be represented by the polynomial remainder:whereis divided byMeanwhile, the elementis defined as the zero polynomial0.

2.2 Rank analysis of matrix over GF(2p)

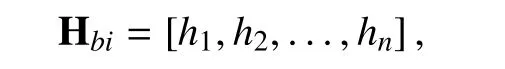
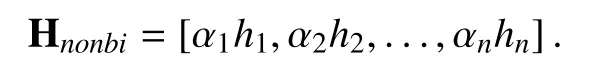
The relation to the rank betweenandis given in the following theorem.

Theorem 1The rank ofequals the rank of

Proof:It is clear that forWe can see from linear algebra [22] that the rank ofequals the maximum number of linearly independent vectors in the vector groupThat is, we only prove that the maximum number of linearly independent vectors in the vector groupequals the maximum number of linearly independent vectors in

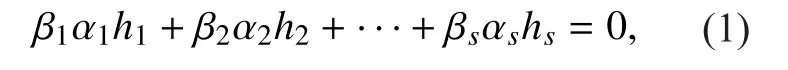
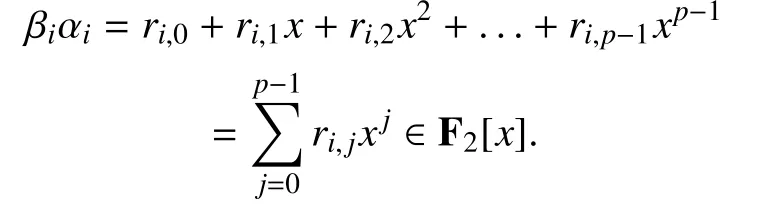
Thus, equation (1) can be written as

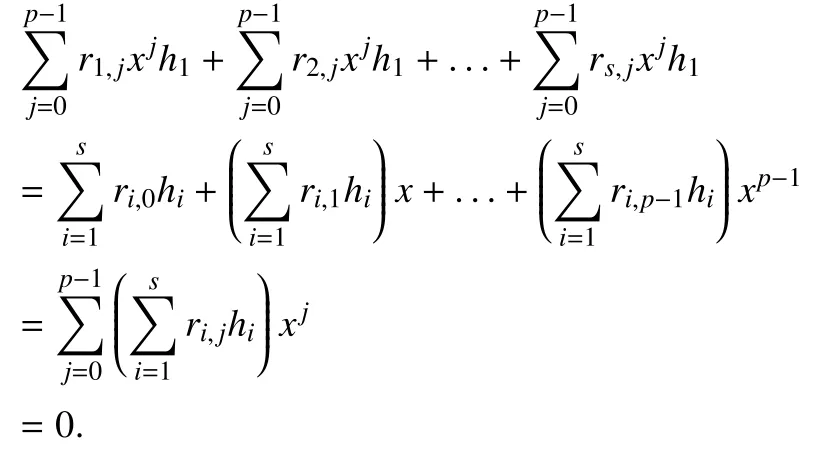
That is,

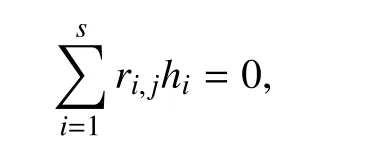
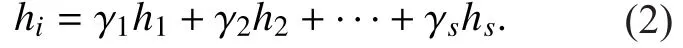
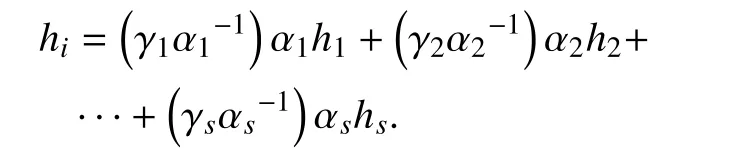
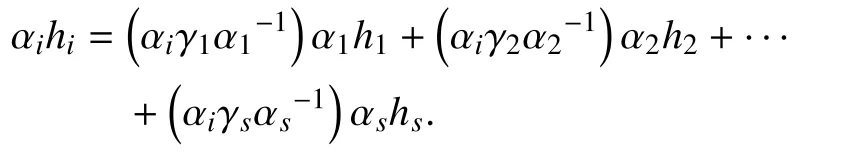
Note that a similar conclusion has been drawn inProposition 4of [20] from the perspective of codewords. Different from their work, we prove it based on linear algebra [22].

Corollary 1Letbe a binary matrix.Replace the ones ofwith the nonzero elements of GF(2p) and form a nonbinary matrixThus the rank ofis equal to or larger than the rank of

For example, consider the following binary matrix

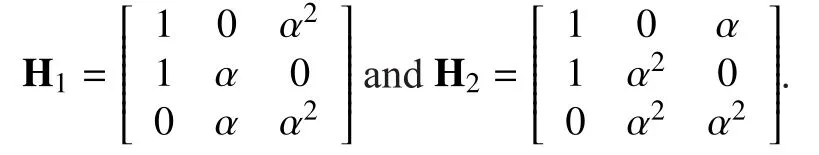
It is easy to see that the ranks ofare 2, 2, and 3, respectively.

By Theorem 1 and Corollary 1, it can be seen that by replacing the nonzero elements ofwith different nonzero elements ofthe rank of the resultingmay increase. Hence, this also provides a theoretical basis for the following construction of nonbinary LDPC codes with flexible code lengths (in bits) and rates.

III. CONSTRUCTION OF FLEXIBLE LDPC CODES OVER GF(2P)

This section will present two methods for constructing flexible LDPC codes overbased on the existing LDPC codes, called the original codes. Here we can take algebraic-based LDPC codes from [23–24] (or references therein) as the original codes.

Method I:We multiply all elements in each column of the parity-check matrixHover GF(2) of the original code by any nonzero element ofand obtain the matrixoverBy Theorem 1, the rank ofis equal to the rank ofH. That is,keeps the same row redundancies ofH. The null space overgives an LDPC code overIf the original LDPC code is nonbinary, we replace the nonzero elements of its parity-check matrix with 1, and then obtain the corresponding matrixHover GF(2).

Method II:We can also multiply the elements in one column (or more columns) of the parity-check matrixHover GF(2) of the original code by more than one nonzero element inTo do so may increase the rank ofoverand simultaneously decrease the row redundancy. A family of LDPC codes overwith various rates can be obtained. Note that reduction of row-redundancy ofmay result in the decoding performance degradation. As the parity- check matrices have large column weights and row redundancies, the resulting codes are suitable for the majority-logic algorithms [5], [25].

Remark 1.Construction inMethod Iis similar to the construction of column-scaled LDPC (CS-LDPC) codes in [20]. The proposed construction inMethod Iis applicable to the parity-check matrices of all existing(binary or nonbinary) LDPC codes and the matrices with large row redundancies, and CS-LDPC codes are constructed from the parity-check matrixHwith the formH=HbiΛ, where Λ is a diagonal matrix. In this sense, the resulting codes fromMethod Ican be employed to construct CS-LDPC codes.Moreover, we can also see fromProposition 4of [20] that the proposed codes have the same minimum symbol Hamming distance as the original codes.

Next, several examples are employed to illustrate the above two methods. The following simulation conditions are given as follows:AWGN channel, BPSK modulation,q-ary sum-product algorithm(QSPA), and the number of iterations is set to be 50.

Example 1.Consider the following 7×7 matrix with rank 4

By multiplying the elements of each column ofHwith the same nonzero elements ofa matrixover GF(2p) with both column and row weight 3 is obtained. The null space overofgives a(7,3)LDPC code overLetp= 2, 4, 5, 6, 7,8. A class of nonbinary (7,3) LDPC codes is constructed. The word error rates (WERs) of these resulting nonbinary (7,3) LDPC codes are depicted in Fig. 1. For the nonbinary(7,3) LDPC code over GF(256), the WERs of this code when decoded with the QSPA(1,3,5,10,50 iterations) are shown in Fig. 2.Also included in Fig. 2 is the finite-length bound [26] of code rate 0.429 and code length 56 bits. We can see from Fig. 2 that, at the WER of 10-6, the nonbinary (7,3) LDPC code over GF(256) when decoded with the QSPA(50 iterations) performs about 0.6 dB away from the finite-length bound. At WER=10-6,there is only 0.25 dB performance gap be-tween 3 and 50 iterations, and the performance curves of 5,10, and 50 iterations overlap each other.

Moreover, it can be seen from Fig. 1 that nonbinary (7,3) LDPC codes overperform better and better with the increase of the field orderThis is reasonable since the equivalent bit length is increasing. However,there exist some special cases, e.g. the following example, that do not meet this feature.

Example 2.Consider the (255,175)EG-LDPC code over GF(256) constructed from the two-dimensional Euclidean geometry EG(2,24) [24]. The matrixHover GF(2)is derived by replacing the nonzero elements of the parity-check matrix of this EG-LDPC code with 1. We can see thatHis a 255×255 matrix which has column and row weight 16,and thatHhas a rank of 80. ByMethod I, a family of algebraic-based (255,175) nonbinary LDPC codes overcan be constructed from this matrixH. Considerp=3,4. The word error performances of these two codes decoded with the QSPA and the iterative soft-reliability-based majority-logic decoding(ISRB-MLGD) algorithm [5] are shown in Fig. 3. Also depicted in Fig. 3 are the WERs of the original (255,175) EG-LDPC code over GF(256) when decoded with the same two iterative algorithms. We can see that at the WER of 10-5, the proposed (255,175) LDPC code over GF(8) and (255,175) LDPC code over GF(16) outperform the original (255,175)EG-LDPC code over GF(256) about 0.4 dB and 0.35 dB, respectively. Notice that for this degree distribution, nonbinary LDPC codes over small field orders (small code length in bits) perform better than ones over high field orders in the low SNR region. Similar results can also be found in [27]. Furthermore, the proposed two codes are suitable for the iterative majority-logic decoding, since only a performance loss of about 0.7 dB is caused by the ISRB-MLGD algorithm compared with the QSPA.

In the following, we take an example to show the effectiveness ofMethod II.

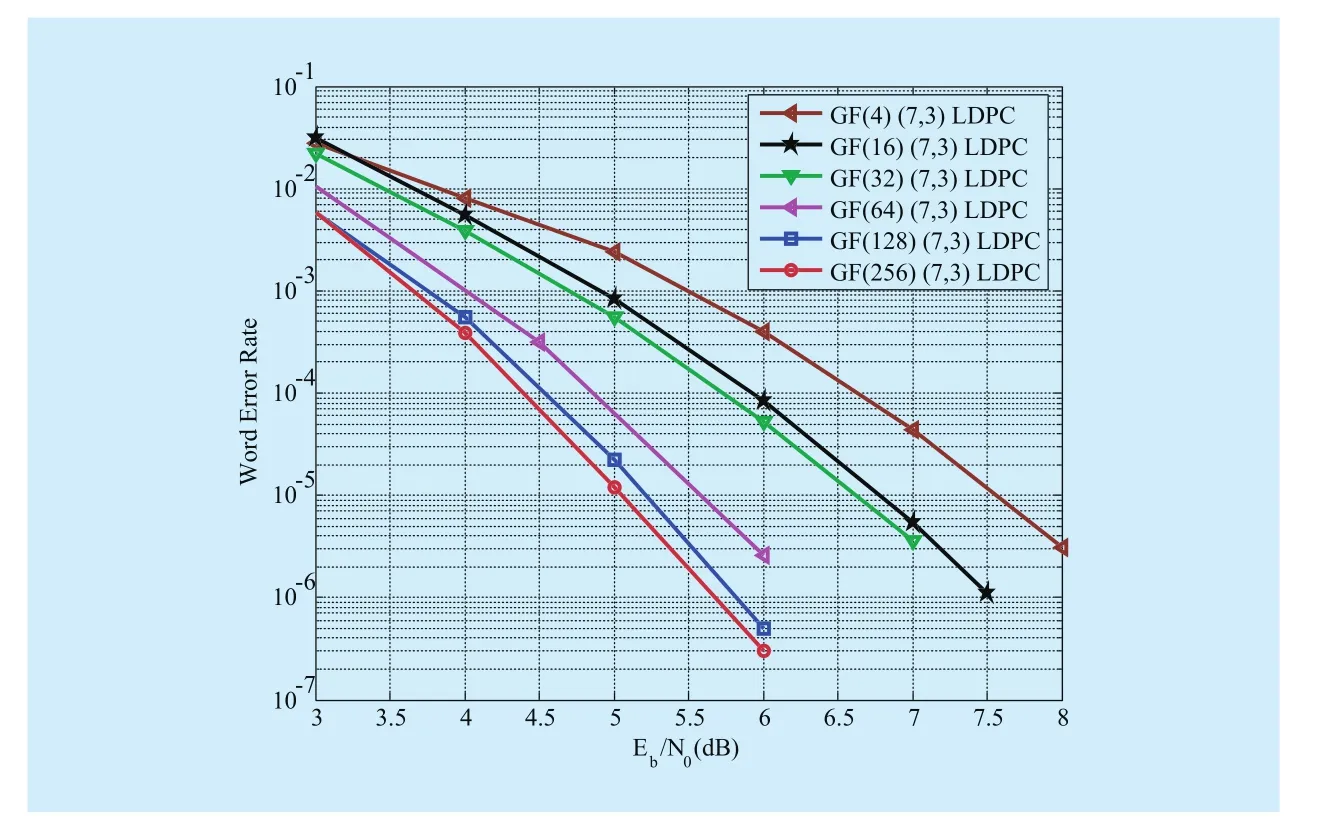
Fig. 1 Word error performances of the (7,3) nonbinary LDPC codes over various finite fields given in Example 1

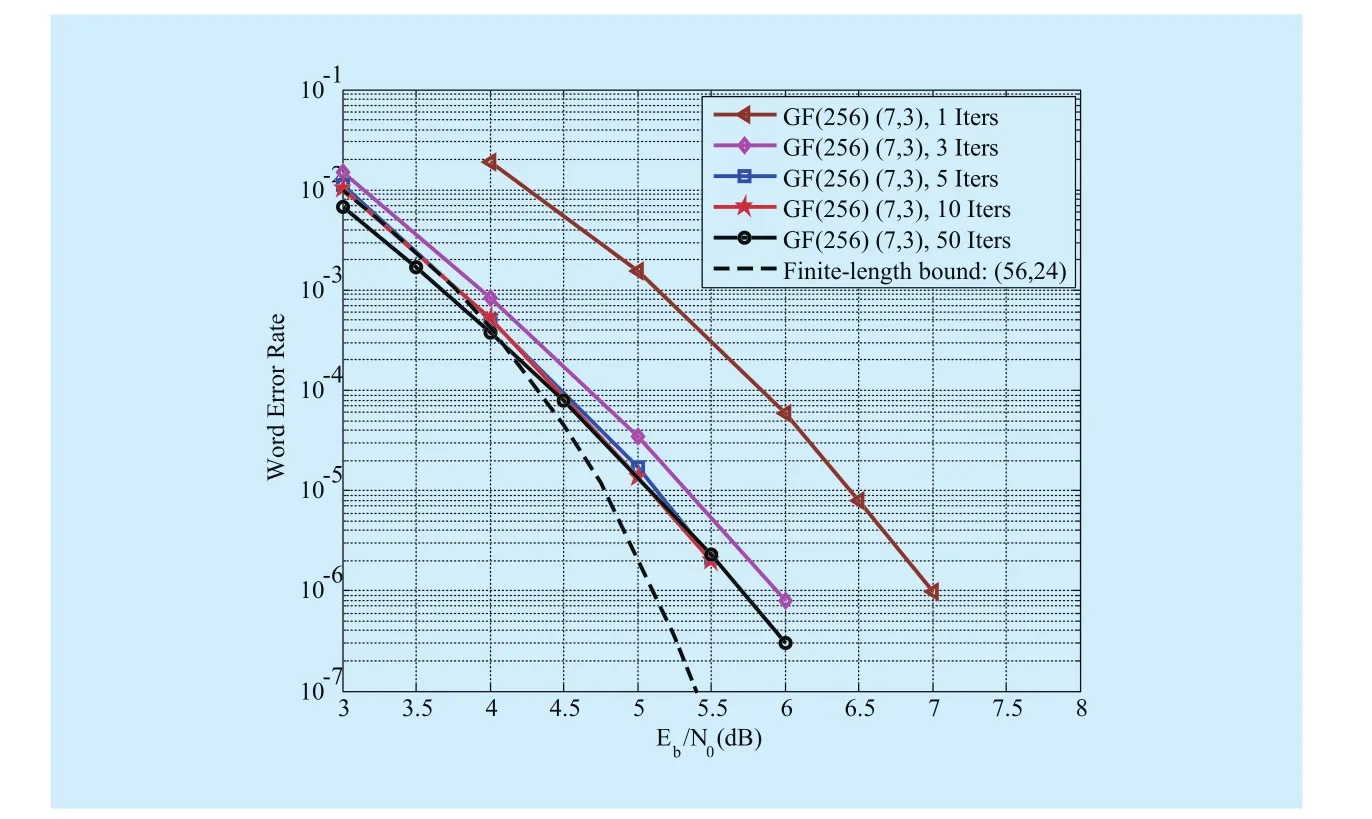
Fig. 2 The convergence rate of decoding of the (7,3) LDPC code over GF(256)given in Example 1

Example 3.Consider the nonbinary quasi-cyclic LDPC cycle codesconstructed from the Singer perfect difference set {0,1,4,6} [Table I, 16]. By replacing the nonzero elements in the parity-check matrix of this code with 1,we can form a binary 26×52 matrixHwhich has column weight 2 and row weight 4. It can be found thatHhas rank 25 and that there exists one redundant row inH. With the use of the proposed two methods andH, we can construct two families of nonbinary LDPC codes:(52,27) LDPC codes overand (52,26)LDPC codes overHere we only consider a (52,26) LDPC code over GF(32). Let the parity-check matrix of this code be

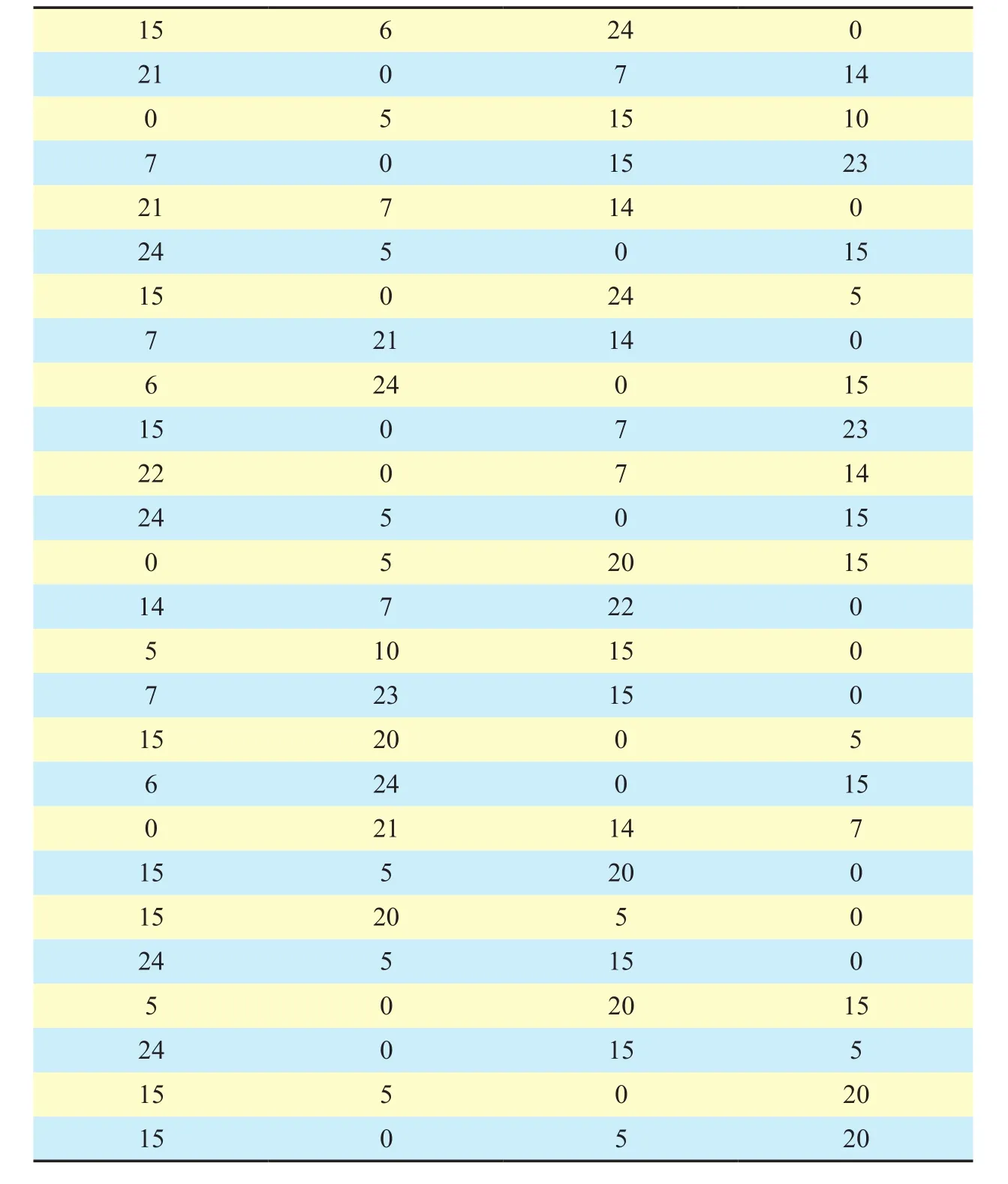
Table I The nonzero field elements of the parity-check matrix of (52,26) nonbinary LDPC code over GF(32) given in Example 3

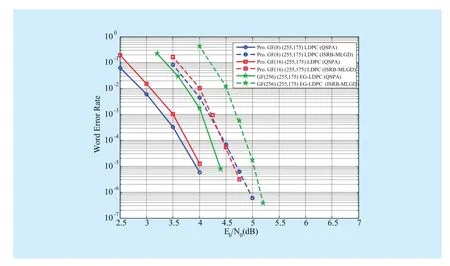
Fig. 3 Word error performances of the proposed (255,175) LDPC code over GF(8), (255,175) LDPC code over GF(16), and the original (255,175) EG-LDPC code decoded with the QSPA and ISRB-MLGD algorithm [5], respectively

In order to study the effect of row redundancy of a parity-check matrix and also to show the performances of nonbinary LDPC codes constructed from the proposed two methods, we simulate several nonbinary LDPC codes constructed based on the binary matrixHinExample 2. In the simulations,AWGN channel with BPSK modulation and the QSPA with 50 iterations are assumed.The bit error performances of these codes are shown in Fig. 5. It can be seen that although(255,170) nonbinary LDPC codes have lower rates than (255,175) nonbinary LDPC codes,they do not have much more coding gain.That is because the parity-check matrices of (255,175) nonbinary LDPC codes have 5 more row redundancies than that of (255,170)nonbinary LDPC codes. Notice that the proposed nonbinary LDPC codes do not have the amazing coding gain, since the matrixHinExample 2has column weight 16. However,this class of nonbinary LDPC codes has fast iterative decoding convergence and can be decoded with the low-complexity decoding algorithms [4-6].

Remark 2. It is generally known that the computational complexity of the QSPA isO(q2), whereqis the field order of the nonbinary LDPC code. Although the fast-Fourier-transform based QSPA (FFT-QSPA) [31]can drastically reduce the computational complexity of the QSPA, its computational complexity is alsoO(qlogq). That is, the computational complexity of the QSPA (or FFT-QSPA)is dominated by the field orderqof the finite field GF(q). From Fig.4, we can see that although our proposed GF(32) (52,26) LDPC code perform as well as GF(256) (32,16)CCSDS-LDPC code, the decoding complexity of our code is much less than that of the CCSDS-LDPC code. On the other hand, the QSPA and FFT-QSPA belong to the iterative algorithm. That is, the number of iterations directly affects the decoding complexity. As shown in Fig. 2, the performance gap of our proposed code between 5 and 50 iterations is negligible. Therefore, the decoding complexity of the proposed nonbinary LDPC codes can be reduced when decoded with the iterative algorithms.

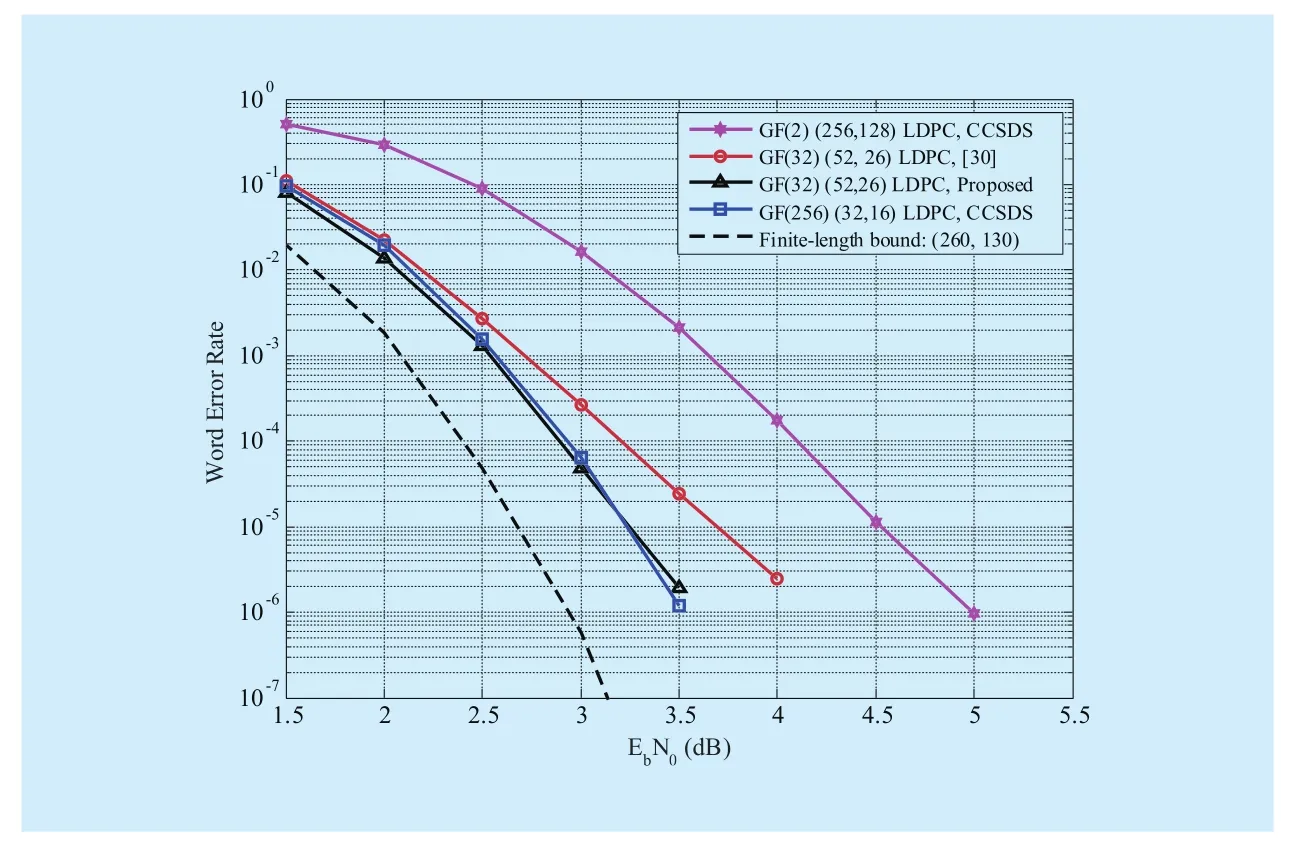
Fig. 4 Word error performances of the constructed (52,26) LDPC code over GF(32) in Example 3 and the comparable binary (256,128) CCSDS-LDPC code[29], (32,16) LDPC code over GF(256)[29], and (52,26) CCSDS-LDPC code over GF(32)[30]

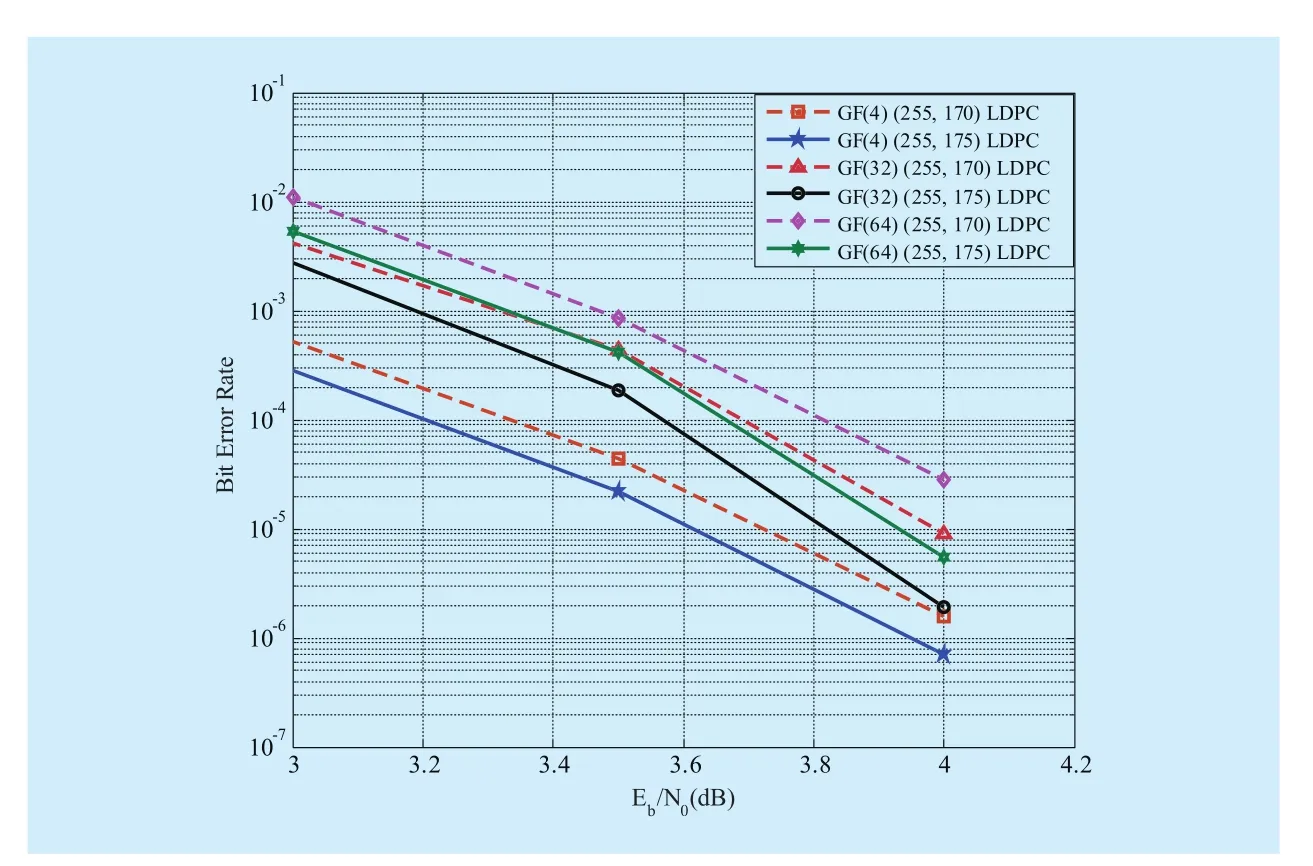
Fig. 5 Bit error performances of the constructed nonbinary (255,175) LDPC codes and (255,170) LDPC codes

IV. CONCLUSIONS

We analyzed the rank of matrices overand proposed two methods for constructing algebraic- based nonbinary LDPC codes. Two classes of nonbinary LDPC codes with flexible field orders and code rates are obtained. Numerical results show that the constructed LDPC codes have good performance and fast iterative decoding convergence.Furthermore, they are suitable for the majority-logic decoding algorithms. So the proposed LDPC codes can be considered for low-latency and high-reliability applications in 5G communication systems.

ACKNOWLEDGEMENTS

This work was supported in part by National Basic Research Program of China under Grant No. 2012CB316100, National Natural Science Foundation of China under Grants 61372074 and 91438101, Joint Funds of the National Natural Science Foundation of China under Grant No. U1504601, and Science and Technology on Communication Networks Laboratory under Grant KX132600032.

[1] R. Gallager, “Low density parity-check codes,”IRE Trans. Inf. Theory, vol.IT-8, no.1, pp 21–28,January 1962.

[2] M. Davey, D. MacKay, “Low-density parity-check codes over GF(q),”IEEE Commun. Lett., vol.2,no.6, pp 165–167, June 1998.

[3] D. Declercq, M. Fossorier, “Decoding algorithms for nonbinary LDPC codes over GF(q),”IEEE Trans. Commun., vol.55, no.4, pp 633–643, April 2007.

[4] C. Chen, Q. Huang, C. Chao, S. Lin, “Two low-complexity reliability-based message-passing algorithms for decoding non-binary LDPC codes,”IEEE Trans. Commun., vol.58, no.11, pp 3140–3147, November 2010.

[5] Q. Huang, M. Zhang, Z. Wang, L. Wang, “Bit-reliability based low-complexity decoding algorithms for non-binary LDPC codes,”IEEE Trans.Commun., vol.62, no.12, pp 4230–4240, December 2014.

[6] M. Zhu, Q. Guo, B. Bai, X. Ma, “Reliability-based joint detection- decoding algorithm for nonbinary LDPC-coded modulation systems,”IEEE Trans. Commun., vol.64, no.1, pp 2–14, January 2016.

[7] D. Qu, L. Li, T. Jiang, “Invertible subset LDPC code for PAPR reduction in OFDM systems with low complexity,”IEEE Transactions on Wireless Communications, vol.13, no.4, pp 2204–2213,April 2014.

[8] L. Li, D. Qu, T. Jiang, “Partition optimization in LDPC-coded OFDM systems with PTS PAPR reduction,”IEEE Transactions on Vehicular Technology, vol.63, no.8, pp 4108–4113, October 2014.

[9] S. Shu, D. Qu, L. Li, T. Jiang, “Invertible subset QC-LDPC codes for PAPR reduction of OFDM signals,”IEEE Transactions on Broadcasting,vol.61, no.2, pp 290–298, June 2015.

[10] H. Xu, D. Feng, R. Luo, B. Bai, “Construction of quasi-cyclic LDPC codes via masking with successive cycle elimination,”IEEE Commun.Lett.,vol.20, no.12, pp 2370–2373, December 2016.

[11] X. Hu, E. Eleftherious, D. Arnold, “Regular and irregular progressive edge-growth Tanner graphs,”IEEE Trans. Inf. Theory, vol.51, no.1, pp 386–398, January 2005.

[12] J. Huang, L. Liu, W. Zhou, S. Zhou, “Large-girth nonbinary QC LDPC codes of various lengths,”IEEE Trans. Commun., vol.58, no.12, pp 3436–3447, December 2010.

[13] S. Song, B. Zhou, S. Lin, K. Abdel-Ghaffar, “A unified approach to the construction of binary and nonbinary quasi-cyclic LDPC codes based on finite fields,”IEEE Trans. Commun., vol.57,no.1, pp 84–93, January 2009.

[14] L. Zeng, L. Lan, Y. Tai, B. Zhou, S. Lin, K. Abdel-Ghaffar, “Construction of nonbinary cyclic,quasi-cyclic and regular LDPC codes: a finite geometry approach,”IEEE Trans. Commun.,vol.56, no.3, pp 378–387, March 2008.

[15] L. Dolecek, D. Divsalar, Y. Sun, B. Amiri, “Non-binary protograph-based LDPC codes: enumerators, analysis, designs,”IEEE Trans. Inf. Theory,vol.60, no.7, pp 3913–3941, July 2014.

[16] C. Chen, B. Bai, X. Wang, “Construction of non-binary quasi-cyclic LDPC cycle codes based on singer perfect difference set,”IEEE Commun.Lett., vol.14, no.2, pp 181–183, February 2010.

[17] J. Li, K. Liu, S. Lin, K. Abdel-Ghaffar, “A matrix-theoretic approach to the construction of non-binary quasi-cyclic LDPC codes,”IEEE Trans.Commun., vol.63, no.4, pp 1057–1068, April 2015.

[18] Q. Huang, K. Liu, Z. Wang, “Low-density arrays of circulant matrices: rank and row-redundancy,QC-LDPC codes,” inProc. IEEE Int. Symp. Inf.Theory, 2012, pp 3073–3077.

[19] L. Zeng, L. Lan, Y. Tai, S. Lin, “Dispersed Reed-Solomon codes for iterative decoding and construction ofq-ary LDPC codes,” inProc. IEEE Global Telecommun. Conf., St. Louis, MO, USA,November/December 2005, pp 1193–1198.

[20] S. Zhao, X. Ma, X. Zhang, B. Bai, “A class of nonbinary LDPC codes with fast encoding and decoding algorithms,”IEEE Trans. Commun.,vol.61, no.1, pp 1–6, January 2013.

[21] R. McEliece, Finite Fields for Computer Scientists and Engineers. Kluwer Academic Publishers, 1987.

[22] S. Friedberg, A. Insel, L. Spence, Linear Algebra.4th ed. New Jersey, USA: Prentice Hall Press,2002.

[23] Q. Diao, Y. Tai, S. Lin, K. Abdel-Ghaffar, “LDPC codes on partial geometries: construction,trapping set structure, and puncturing,”IEEE Trans. Inf. Theory, vol.59, no.12, pp 7898–7914,December 2013.

[24] W. Ryan, S. Lin, Channel Codes: Classical and Modern. New York, USA: Cambridge Univ.,2009.

[25] D. Zhao, X. Ma, C. Chen, B. Bai, “A low complexity decoding algorithm for majority-logic decodable nonbinary LDPC codes,”IEEE Commun.Lett., vol.14, no.11, pp 1062–1064, November 2010.

[26] Y. Polyanskiy, H. Poor, S. Verdu, “Channel coding rate in the finite blocklength regime,”IEEE Trans. Inf. Theory, vol.56, no.5, pp 2307–2359,May 2010.

[27] C. Chen, B. Bai, Z. Li, X. Yang, L. Li, “Nonbinary cyclic LDPC codes derived from idempotents and modular golomb rulers,”IEEE Trans. Commun., vol.60, no.3, pp 661–668, March 2012.

[28] C. Poulliat, M. Fossorier, D. Declercq, “Design of regular (2,dc) LDPC codes over GF(q) using their binary images,”IEEE Trans. Commun., vol.56,no.10, pp 1626–1635, October 2008.

[29] Short Block Length LDPC Codes for TC Synchronization and Channel Coding, CCSDS 231.1-O-1, 2015.

[30] H. Xu, B. Bai, “Superposition construction ofq-ary LDPC codes by jointly optimizing girth and number of shortest cycles,”IEEE Commun.Lett., vol.20, no.7, pp 1285–1288, July 2016.

[31] D. MacKay, M. Davey, “Evaluation of Gallager codes of short block length and high rate applications,” inProc. IMA International Conference on Mathematics and Its Applications: Codes, Systems and Graphical Models, New York, Springer-Verlag, 2000, pp 113–130.