ComRank: Joint Weight Technique for the Identification of Influential Communities

Muhammad Azam Zia, Zhongbao Zhang, Ximing Li, Haseeb Ahmad, Sen Su

State key Laboratory of Networking and Switching Technology,

Beijing University of Posts and Telecommunications, No.10 Xitucheng Road, Beijing, China

* The corresponding author, email: susen@bupt.edu.cn

I. INTRODUCTION

Online social networks (OSNs) have achieved an immense esteem while experiencing rapid growth during the past decade [1]. The leading forums of the OSNs include Faceboook [2],Twitter [3], Sina Weibo [4] etc. Bibliographic data banks (DBs) such as Google Scholar,DBLP [5] and ArnetMiner, provide the platform to the scholars for sharing their ideas,information and research contents in more appropriate manner. Identifying the leading communities in social networks is of great significance for the researchers of respective domains. More precisely, taking OSNs into account, our central objective is to extract the most influential communities. Hence, the objective could be accomplished by finding the rank of different communities in order to extract the leading ones.

Community is one of the core feature of OSNs, which could be either a person, group of people, topic or a venue etc. Different communities are expected to play different roles in OSNs. In this study, the term community refers to the research community of OSNs. The rapid growth in OSNs research has made it increasingly important to extract the qualitative and quantitative insights of different communities. The influence of a community entirely depends on the quality of research contents.The quality of these contents is usually determined by the level of innovation, diversity and efficiency of solutions towards the key scientific problems. The more qualitative work gets more admiration in terms of score that leads towards increment in its influence. Therefore,this incremented influence uplifts the rank of underlying community. Finally, the top ranked communities are extracted in OSNs that attract the scholars’ attention for getting more insights about the latest research problems and their intended solutions.

In this paper, the authors introduced a new idea by considering joint weight to find out the communities ranking and their influence.

There exists a bulk quantity of literature that presents the deep insights of OSNs. However, there exists significant variation among the presented solutions. As an application of OSNs, community ranking techniques are based on link analysis that is usually performed by employing the iterative process. Among iterative approaches, the state of the art algorithm [6, 7] is utilized as the foundation for ranking purposes in the literature. While forming a directed graph, these proposals consider communities as vertices as a replacement of pages. These directed graphs represent relationship associations. In this scenario, PageRank ranks a community as significant one, if there are several other communities referencing it. Thus, the rank of a community is distributed among all of the connected communities. This algorithm actually considers backlinks in these studies.

There are a lot of contributions put forward by academic communities that address the key issues of OSNs [8-12] and citation networks(CNs) while providing the appropriate solutions. However, none among [13-16] focused towards finding the top ranked research communities. The influence extraction of communities is also considered by few researchers[17, 18]. However, the authors performed the analysis while taking limited communities in to account. Therefore, these works are not scalable to extend for larger datasets. Thus,we get motivation to fill the gap in order to provide influential community based analysis while considering a large dataset. Our work is innovative comparative to others because it incorporates internal and external aggregation weight count amongst different communities.In more details, we count the strength that a community gets from itself and also the ones gained by the other communities. Thus, we get the aggregation weight count based on these parameters that helps for figuring out the top ranked communities with respect to defined levels [19]. Moreover, we also consider the effect of indegree of cited community during joint weight calculation process.

Three main contributions of proposed work for ranking a large number of communities based on aggregation weight are presented as follows:

1) First, this is the pioneer attempt to consider the internal and external citation factors along with indegree of a CN. These factors are taken into account for realizing the individual strength of communities and their effect upon each other. Thus, joint weight is calculated based on aforementioned latent factors in CN.

2) Second, we put forward a community ranking algorithm (ComRank) by modifying standard PageRank algorithm. More precisely,the modification is actually made to evaluate the quality of the communities while considering the joint weight based transition matrix.Thus, the ranking of the most influential communities is done by the proposed algorithm.

3) Third, after performing extensive experiments on social network dataset, the leading communities are extracted that reveal their actual influence with respect to many other communities within CN. Finally, the obtained results are compared with the results of standard PageRank algorithm. The comparative study highlights that the proposed ComRank outperforms the standard PageRank in terms of ranking communities. Further, it is remarked that proposed technique requires less substantial computations for larger dataset as compared to standard PageRank algorithm.For instance, we use larger dataset of CN to validate the proposed ComRank algorithm.

The rest of paper is organized into following sections. First, we describe related work along with their limitations is discussed in Section 2.The problem statement is described in Section 3. Section 4 describes our strategy to compute joint weights as well as the detailed insights of the proposed ComRank algorithm. Section 5 presents the experimental evaluation and comparative studies. Finally, Section 6 concludes the precise theme of our study.

II. RELATED WORK

There are a lot of contributions put forward by academic communities that address the key issues of OSNs and CNs. In more details,within OSNs domain, researchers are mainly focused towards learning user behavior [9],mining the user interest or community leaders[10, 11], trends and trend setters [12]. Considering DBs, the researchers proposed the mechanisms either to find research leaders [10] or evaluating user influence [14]. Some works studied the co-author relationships [15], while others performed the citation analysis [16].But none among them focused towards finding the top ranked research venues (conferences).The influence of venues is also considered by few researchers [17, 18]. However, the authors performed the analysis while taking limited communities into an account. Moreover, these works are not scalable to extend for larger datasets. Thus, we get motivation to fill the gap in order to provide community based analysis while considering a large ArnetMiner dataset of different communities.

Working toward community based analysis;Ma et al. [16] were the first who utilized the PageRank algorithm (PRA) for integer citation analysis. The authors put forward an incredible idea while presenting PRA indicator as robust dimension that presents the academic influence of scientific contents. However, similar to many others, their study were also limited to specific domain of venues. Rahm and Thor [18] analyzed the citation frequencies of conferences and journals database to perform citation analysis and concluded that the conferences citation impact is higher than the journals. However, their citation analysis was limited to specific communities and not scalable for larger dataset, which makes it not the most suitable candidate. Moreover, the selection of threshold values of damping factor still remained a topic to be focused appropriately.

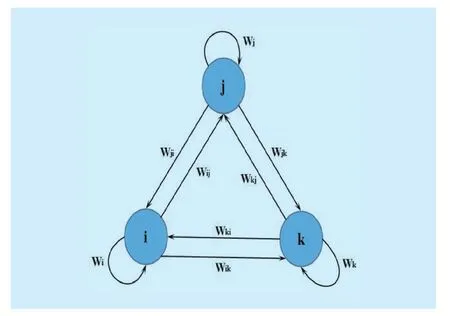
Fig. 1 Relationships between communities

Zaïane et al. put forward a prototype that employed random walk strategy in order to extract knowledge of research communities and their collaborations [20]. However, the presented approach requires expensive computations of matrix multiplications. Another review work is put forward by Waltman and Yan [21], in which different ways of extracting the most influential communities among citation network are discussed in detail. The authors discussed to provide more weights to contents cited by highly influential venues such as Nature and Science while usual weight to the ordinary journals. Further, the usage of PR algorithm and its working in details is also discussed in the same paper. Li et al. [22] put forward linear time online search algorithm for extracting topkinfluential communities within OSNs. Further, the authors provided an indexed structure for improving the efficiency of their algorithm. Effendy et al. diverted the attention towards categorizing the conference with respect to their influence [23]. The authors provided the details about the existing four categorization platforms while pointing out their limitations. However, not a single approach was presented to address these limitations. Different from ordinary citation analysis that work at the contents level that is citation count, our work focuses on inter and intra citation aggregation weight count amongst different communities. Further, we also validate our results while comparing with well-known conference ranking portals [19, 24]

III. PROBLEM STATEMENT

3.1 Citation network (CN)

3.2 Problem definition

LetG(V,E,W) be a weighted DAG that refers to an underlying CN, where V stands for the communities, E is denoting the relationships among different communities, while W is representing the weight strength of each edge.Suppose that the nodesare representing the total number of communities withwhere each node contains the citation information of utmostNyears of distinct community. More precisely, the edgeindicates the flow of information from nodejtoiand vice versa. Similarlyare denoting the external and internal weights of a communityirespectively. Based on these external and internal weights, a transition matrixW'is constructed. Finally, the ComRank ranks the communities based onW'.

IV. PROPOSED COMMUNITY RANKING ALGORITHM (ComRank)

In this section, first we provide the details of standard followed by its limitations. Later,we describe the necessary changes that are required to consider the latent features of CNs.Subsequently, we provide the mathematical notion of joint weights that are used to construct a transition matrix. Finally, we explain the outline ofalgorithm.

4.1 Standard PageRank Algorithm

It is an effective algorithm that ranks the web pages by considering the human attention and interest devoted to them. A hyperlink in it reflects an endorsement correlation. The ranking criteria of web pages through it are quite straightforward. For instance, the rank of a webpage is actually a measure of the numbers and quality of other web pages that are linked to it [18, 24]. The following equation presents the standard

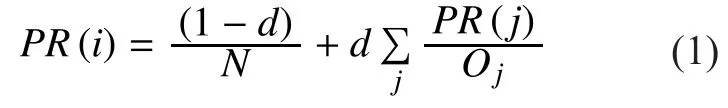
Based on the given equation (1), we found numerous observations that are described below: 1) The PR is directly dependent on the quantity of web pages that link to; 2) the PR of web pagewill be high if the PR value of linked web pageis high; 3) the PR of the web pagewill be high if the web pagelinked to least number of other web pages; 4)the value of damping factorhas an effect on PR.

Therefore, the main idea of PRA for a web pagecan be described in details as follows.If pageis important, there must be a greater number of web pages that would be connected to it. Moreover, the pages connect to it should be important by themselves as well [29]. That is “the importance of the page is “voted” by all other pages in the Web”. Thus, the definition of the PR value of each page is defined as follows:

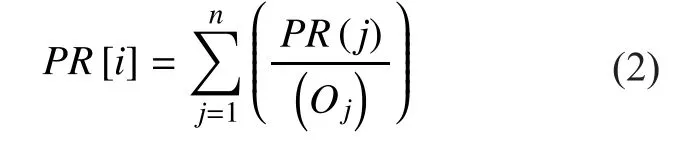
The solution of this formula is:wheredenotes the count of user surfing the webpage.is the initial rank value of each page, and in the first definitionis defined as uniform distribution andis the connection matrix of each page. An issue ofis that some pages may not have the outgoing links. Thus, when some pages are linked to the non-outgoing page, all the value will be sunk into underlying page. We call this kind of page “damping node”. The most common way to deal with the “damping node” is to assume that the surfer will start a complete new web,which does not have the connection to the“damping node”. To eliminate the situation,the matrix is changed to:wherendenotes the total number of the pages in the web, andis the matrix whose column element is 1.

4.2 Limitations of PageRank

We found that PageRank face several drawbacks as follows:

1) It only considers external influence of each page due to the existence of hyperlinks among them. 2) The structure used for CN analysis is only a DAG without weights. However in our scenario, we consider the CNs as directed DAGs with weights. 3) PageRank also ignores the internal influence, because the hyperlinks do not link to themselves.

Therefore, the essential requirement of community influence analysis problem is to consider the weights along with internal and external influence. Thus, the presented joint weight equation incorporates all of the aforementioned features. Consequently, the main objective of the proposed algorithm is to identify the most influential nodes, which refer the communities in the CNs.

4.3 ComRank Algorithm

The underlying subsection presents the proposed notion of joint weight that considers three main features in details, including internal and external citation along with indegree of cited community. Subsequently, this notion is utilized to construct the weight matrixWthat is normalized according to prescribed procedure to get a transition matrixW'. Lastly, a modified version of standard PRA, i.e.,ComRank, is proposed that incorporates the transition matrix to rank the communities in a novel way.

4.3.1 Joint weight

A novel method to solve the key problem of ranking the scientific communities, based on joint weights in CN is presented in this section. First, we briefly explain the concept of joint weights based on citations that a community acquires internally as well as from external communities.

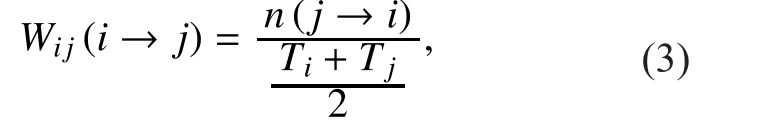
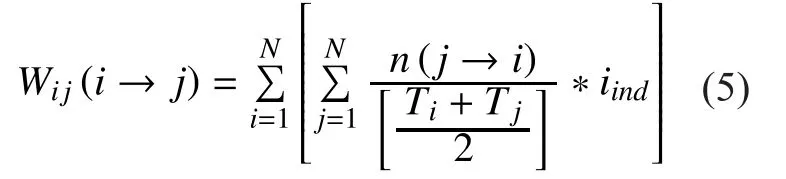
4.3.2 Transition matrix

The weight matrix of all the nodes is calculated by employing the aforementioned joint weight equation. Weight matrix is actually a square matrix with rows and columns that con-tains the information about citation relationship based on joint weights. If there present an edge from source node to the destination node whose weight value is zero. A random vector over the citation relationship that corresponds to a source of rank is applied to the weight matrix. Therefore, the added vector is normalized for controlling the sparseness of the matrix. Thus, the final equation of transition matrix is presented as follows:

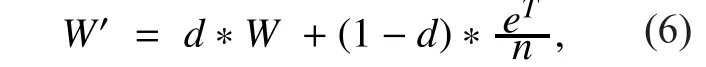
whereWis the weight matrix andis the uniform matrix divided by the number of nodesn. Note thatd＜1 and it works the same as the damping factor of PRA. During the calculation, the rank vector of each node and the dimension of the vector is given by (n,1).The initial rank value of each node is set (1/n).Thus, the modified weight matrixW'is generated based onW, while the purpose of the including expressionto this formula is to erase all the column vectors having zero joint weight value, which means that the node does not have any connection with others. If we do not consider this factor, the rank value of node becomes null. Power method is applied to calculate the rank and to compare the difference between subsequent iterations. The value is said to be converged, when the differencebetween subsequent iterations remains negligible.

Algorithm ComRank: Input: weight matrix

Algorithm ComRank: Input: weight matrix

ComRank is modified based on the standard PRA and applied on the refined dataset in order to extract the most influential communities in CN. Here, we remark that PRA has some limitations when applied to the CN analysis problem. For instance, considers external influence that affects the rank value of pages. While performing the CN analysis;the structure of standard PRA employs a directed graph of links without weights. Thus,the actual influence of an external link cannot be checked without weight strength. Hence,our actual contribution is the introduction of weights parameter within ComRank for checking community level influence. More precisely, we consider the CN as DAG with weights. Moreover, PRA also ignores the internal influence as hyperlinks do not point to themselves. Thus, ComRank uses the DAG along with weights and considers internal and external influence of the communities as well.Finally, the main objective of ComRank is to identify the most influential nodes of CN.

4.3.3 Algorithm outline

The PageRankis an eigenvector special matrix,which is defined as follows:

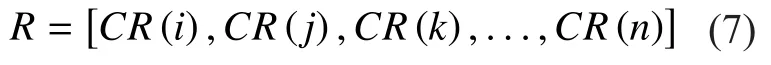
The rank of communities can be calculated in an iterative way, the calculation steps performed as mentioned in [1]. The execution of the ComRank algorithm is described in following steps while the graphical illustration of proposed algorithm is depicted in Fig. 2.

First, threshold value is used to compare the difference between subsequent iteration results as mentioned in step 1. Subsequently,set the damping factor in step 2. Next, set the initial rank value of each node. Load the weight matrix and transform the weight matrix to generate transition matrix W’ in steps 3 to 7. Afterwards, calculate and note the first iteration result as produced in step 8. Then,continue iterative process from steps 9-14. Fi-nally, sort according to rank vector value.

V. EXPERIMENTAL RESULTS

5.1 Experimental setup

We considered CN as a social network in this study and the dataset is taken from ArnetMiner[30], which is publically available online. It is comprised of publications and citation information. In more details, it contains 2,244,021 papers with 4,354,534 citations related to computer science communities. First, we normalized the dataset for the evaluation of our proposed method. The normalized dataset contains the index of paper, authors name, title of the paper, venue, abstract and citations information. The extracted dataset information is ranging from 2008 to 2012 and it holds 7205 venues and 3293 established connections.For our work, scientific communities are considered as a DAG, in which each vertex represents a community, while edge link denotes citation relationship between communities. If no citation is reported between two communities, then the edge weight becomes zero and later damping procedure is applied to normalize the process. Finally, the proposed method is executed on refined dataset and influential communities are extracted.

5.2 Experimental results and analysis

ComRank incorporates joint weight that is calculated based on equation (5). After applying the proposed method to the CN, the rank of significant communities is obtained.Experiments are repeated several times to produce ranks through iterative process. The top ranked communities with maximum influence level through the presented novel method are thus extracted out. We separated the results of ComRank top 15 communities and compared with the standard PRA. As a result, we achieved much better results than the standard PRA for this case study by extracting all the high level conferences, while standard PRA also nominated some low level conferences at high rank according to the calculated values as depicted in Fig 3.

It is clear that ComRank achieved better results than the standard PRA, in which low level conferences are also considered as high level conferences. For example, SAC (ACM/SIGAPP Symposium on Applied Computing)is a C level conference with comparatively smallerEstimated Impact of Conference(EIC)value [24], but the standard PRA extracted it as a top ranked conference. Similarly,instead of A level, PRA designated some B level conferences within top 10 ranks. On the other hand, proposed algorithm detected only level A (topped ranked) conferences in top 10 rankings. The top 15 communities produced by presented technique consist of 13 A and 2 B level communities having EIC values more than 0.9, while more B and C level communities are recorded in the results produced by standard PRA with comparatively low EIC values (for instance 0.79), as presented in Table 1.

The top 15 communities are ranked from 1 to 15 by ComRank but PRA designated them as lower level communities comparative to proposed algorithm. For instance, top 10 rank positions are assigned to only A level conferences with more than 0.90 EIC worth by ComRank algorithm but baseline algorithm provided top ranked positions to many B and C level conferences with less EIC worth as well. The AAAI conference, which is an A level community, got top rank position by our technique but baseline assigned 5th rank to the same venue. The proposed algorithm did not rank SAC conference even among top 15 communities, because it is not worthy of getting that position. Thus, it is another perspective that proves the significance of the proposed technique for community ranking within CNs.

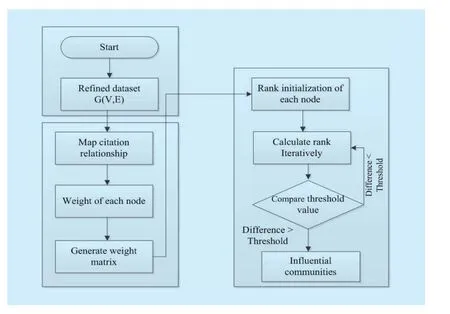
Fig. 2 Graphical viewpoint of proposed study

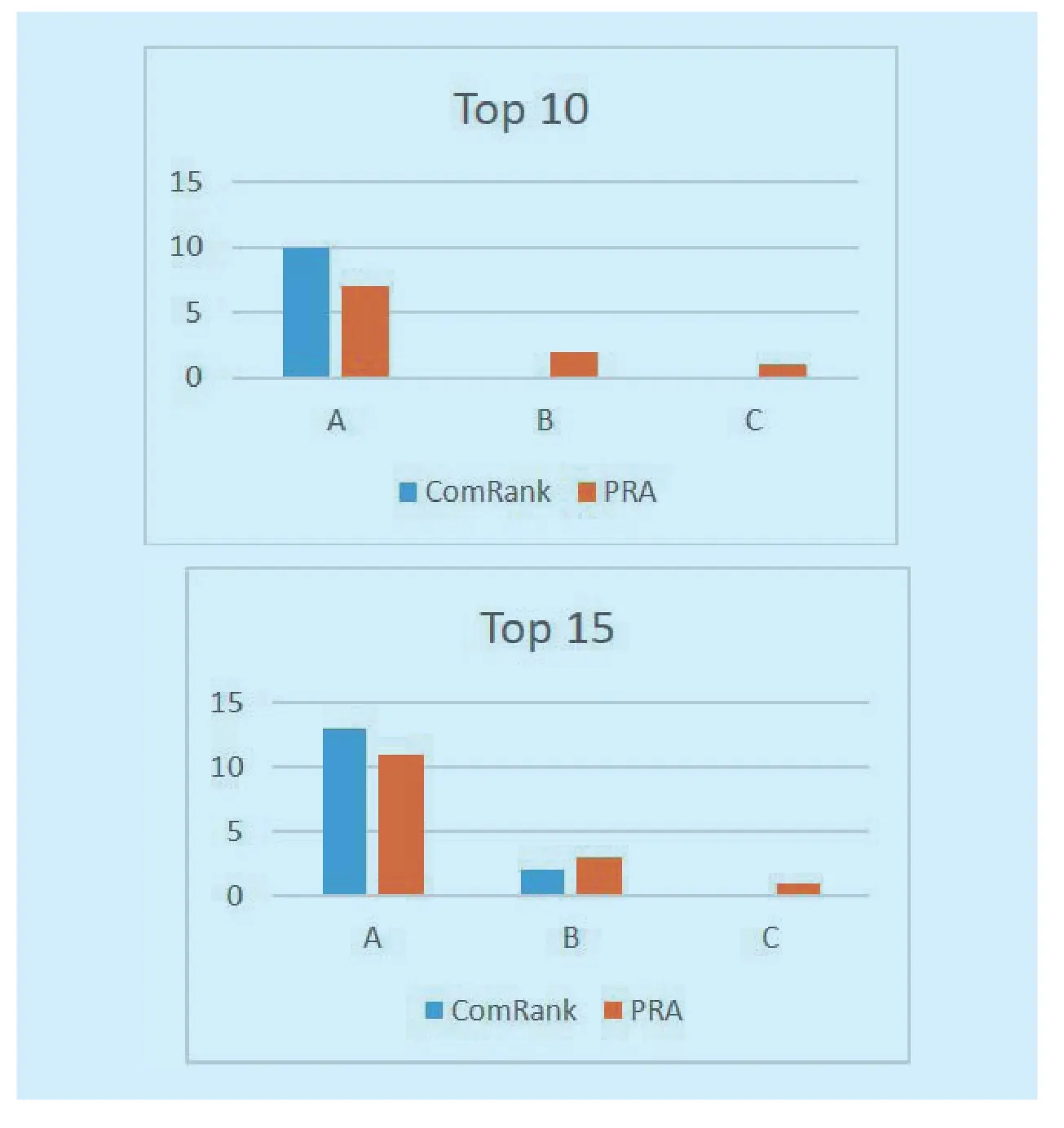
Fig. 3 Graphs showing the comparison between the levels of top 10 and 15

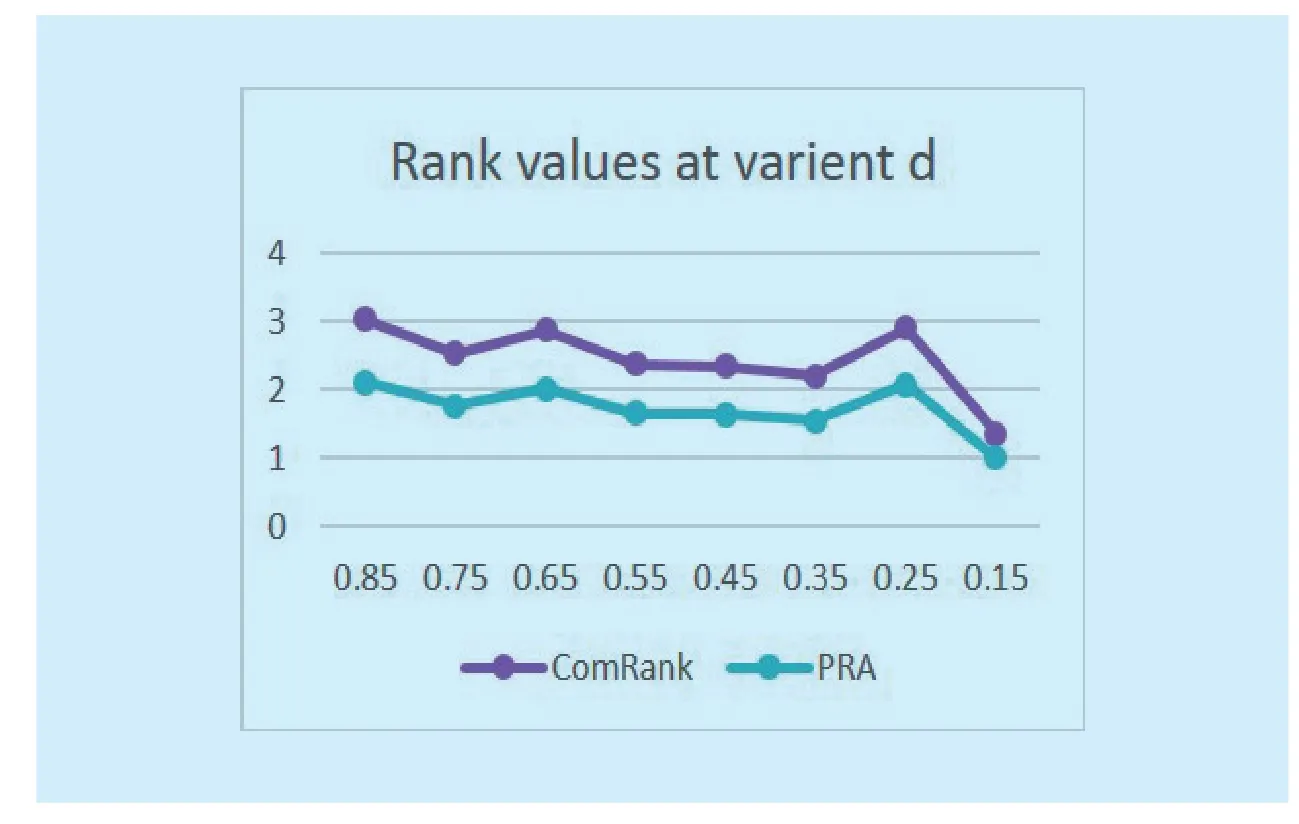
Fig. 4 Comparison between the rank values for variant damping factor

Fig. 4 presents the maximum rank values produced by both ComRank and the standard PageRank with various damping factors. As already explained, the damping factor value is always taken from 0 to 1. During experimental setup, various values of d are set for the proposed algorithm and standard PageRank to analyze the effect on rank values. It is noted that rank values produced by our technique are comparatively higher than PageRank. The maximum rank value produced by our technique is 3.02, while 2.10 is resulted by PRA withd=0.85 for the top ranked community.

5.2.1 Computational cost

The computational complexity of PRA iswheredenotes the network size.While, the proposed ComRank algorithm converges even in less iterations, thus the computational complexity is less thanMore precisely, in our case, PRA converges in total of 84 iterations, while ComRank converges in 70 iterations. The time took by PRA was about 0.95 seconds, while our proposed algorithm converged in 0.75 seconds.

VI. CONCLUSION

In this paper, we introduced a new idea by considering joint weight to find out the communities ranking and their influence. First, we consider the internal and external citation factors along with indegree of a citation network.The joint weight considers both internal and external mentions. Moreover, network centrality factor of cited community is also used as a multiplying factor. Second, a community ranking algorithm ComRank is proposed that considers joint weight in order to rank and identify impact of each community. Extensive experiments are performed to evaluate the influence and rank of each community in the citation networks. Finally, the extracted leadingcommunities revealed their actual influence with respect to many other communities. The comparative analysis presents that ComRank extracted high ranked communities in terms of level and EIC worth, while the PageRank foretold some low level communities at high ranks. Thus, the presented work attempts to highlight the importance of communities from an innovative perspective.

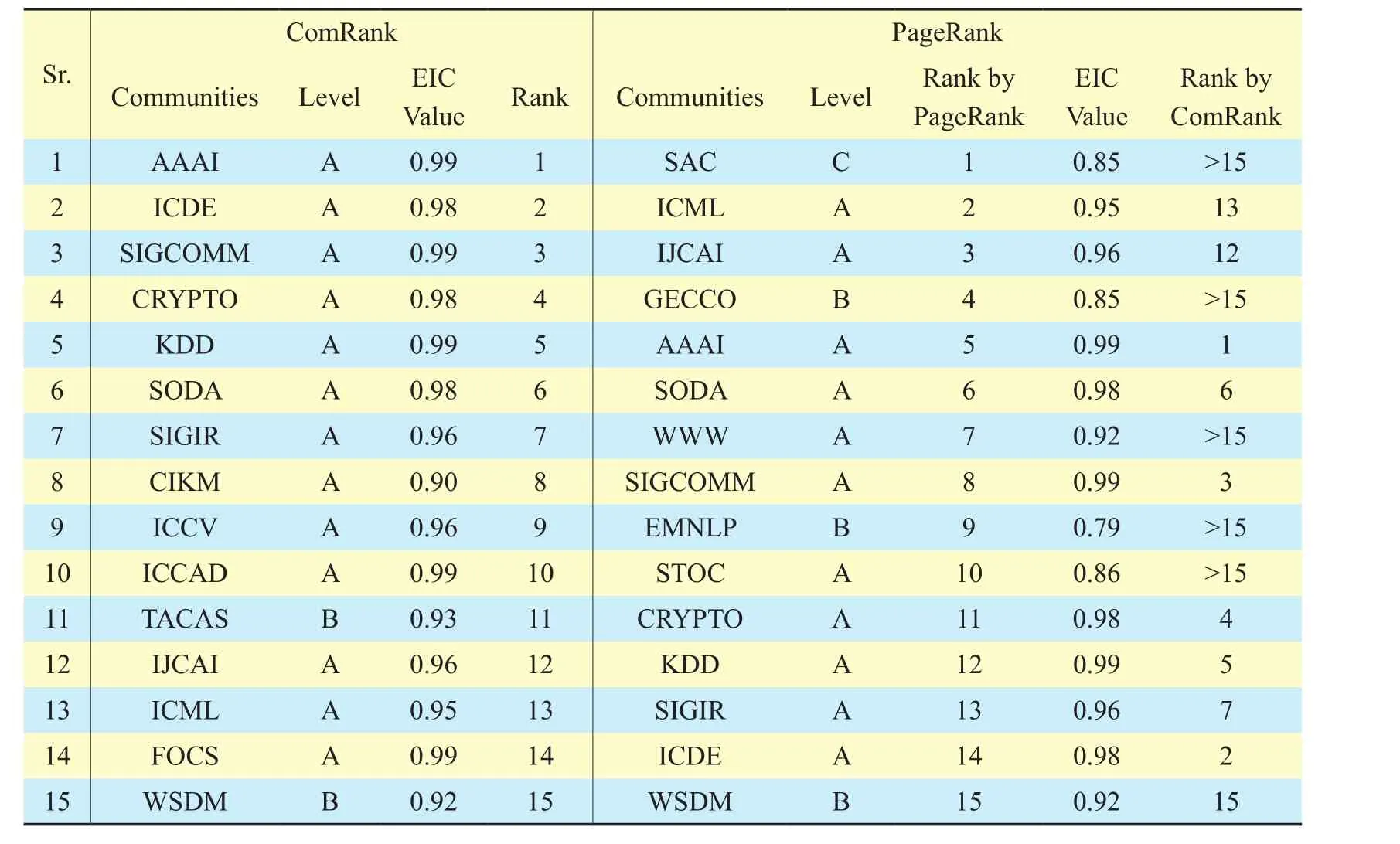
Table I Communities extracted by ComRank and PRA along with their levels and EIC worth

ACKNOWLEDGEMENT

This work was supported in part by the following funding agencies of China: National Natural Science Foundation under Grant 61170274, 61602050 and U1534201.

[1] L. Liu and H. Liang, "Influence analysis for celebrities via public cloud and social platform",China Communications,vol. 13, no. 8 (2016):53-62.

[2] http://www.facebook.com

[3] http://www.twitter.com

[4] http://www.sinaweibo.com

[5] http://dblp.uni-trier.de/

[6] L. Page, S. Brin, R. Motwani, and T. Winograd,"The PageRank citation ranking: bringing order to the web", 1999.

[7] D. Ying, E. Yan, A. Frazho and J. Caverlee,"PageRank for ranking authors in co-citation networks.",Journal of the American Society for Information Science and Technology, vol. 60, no.11 (2009): 2229-2243.

[8] W. Yanben and C. Wandong, "Epidemic spreading model based on social active degree in social networks", [J]China Communications,vol. 12, no. 12 (2015): 101-108.

[9] L. Zhang, T. Zhou, Q. Zhixin, L. Guo and L. Xu,"The research on e-mail Users' behavior of participating in Subjects based on social network analysis", [J]China Communications, vol. 13, no.4 (2016): 70-80.

[10] R. Wang, W. Zhang, H. Deng, N. Wang, Q. Miao,and X. Zhao, "Discover community leader in social network with pageRank.",In Advances in Swarm Intelligence, (2013): 154-162.

[11] H. Li, J. Yan, H. Weihong and D. Zhaoyun, “Mining user interest in microblogs with user-topic model”,China communications, vol. 11 no. 8(2014):131-144.

[12] G. B. Orgaz, H. Menéndez, S. Okazaki, and D.Camacho, "Combining social-based data mining techniques to extract collective trends from twitter",Malaysian Journal of Computer Science,2014.

[13] B. L. Alves, F. Benevenuto, and A. H. F. Laender,"The role of research leaders on the evolution of scientific communities",In Proceedings of the 22nd international conference on World Wide Web companion, pp 649-656.

[14] J. Wei, G. Mengdi, W. Xiaoxi and W. Xianda, “A new evaluation algorithm for the influence of user in social network”,China Communications,vol. 13 no. 2 (2016): 200-206.

[15] A. Daud, M. Ahmad, M. S. I. Malik, and D. Che,"Using machine learning techniques for rising star prediction in co-author network”,Scientometrics, vol. 102, no. 2 (2015):1687-1711.

[16] N. Ma, J. Guan, and Y. Zhao. "Bringing PageRank to the citation analysis",Information Processing& Management,vol. 44, no. 2 (2008):800-810.

[17] H. Baumgartner and R. Pieters, “The influence of marketing journals: A citation analysis of the discipline and its sub-areas”, No. December. Tilburg,The Netherlands: Tilburg University, 2000.

[18] E. Rahm and A. Thor, "Citation analysis of database publications",ACM Sigmod Recordvol. 34,no. 4 (2005): 48-53.

[19] http://www.ntu.edu.sg/home/assourav/crank.html

[20] O. R. Zaiane, J. Chen and R. Goebel, "Mining research communities in bibliographical data",Advances in web mining and web usage analysis. Springer Berlin Heidelberg, 2009. 59-76.

[21] L. Waltman and E. Yan, "PageRank-related methods for analyzing citation networks",In measuring scholarly impact, Springer International Publishing, (2014):83-100.

[22] R-H. Li, L. Qin, J. X. Yu, and R. Mao, "Influential community search in large networks",Proceedings of the VLDB Endowmentvol. 8, no. 5 (2015):509-520.

[23] S. Effendy and Yap, R. H, “The Problem of Categorizing Conferences in Computer Science”,In International Conference on Theory and Practice of Digital Libraries,pp:447-450. Springer International Publishing.

[24] http://perso.crans.org/～genest/conf.html

[25] H. F. Moed, “Citation analysis of scientific journals and journal impact measures”,Current Science, vol. 89, no. 12, 2005.

[26] D. Fiala, "Mining citation information from Cite-Seer data."Scientometrics, vol. 86, no. 3 (2010):553-562.

[27] P. Chen, H. Xie, S. Maslov, and S. Redner, "Finding scientific gems with Google’s PageRank algorithm",Journal of Informetrics,vol.1, no. 1(2007): 8-15.

[28] E. Yan and Y. Ding, "Discovering author impact:A PageRank perspective",Information processing & management, vol.47, no. 1 (2011):125-134.

[29] J. Li, and P. Willett, "ArticleRank: a PageR-ank-based alternative to numbers of citations for analysing citation networks",In Aslib Proceedings, vol. 61, no. 6 (2009): 605-618.

[30] J. Tang, J. Zhang, L. Yao, J. Li, L. Zhang, and Z. Su,"Arnetminer: extraction and mining of academic social networks",In Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and data mining, (2008):990-998.