采用基因表达式编程的沟灌入渗模型参数估计方法

刘 琨，黄冠华

（1.中国农业大学 水利与土木工程学院，北京 100083；2.中国－以色列国际农业研究培训中心，北京 100083）

1 研究背景

相比于有压灌溉，沟灌具有低能耗和低投入的优点，被广泛用于宽行作物，例如棉花，玉米和蔬菜。然而，由于沟灌系统的设计不合理，导致灌溉水利用效率较低，甚至引起次生盐碱化和地下水污染等问题［1］。通过对沟灌系统的优化设计，可以极大地提高灌水效率［2］。然而，通过田间试验的方法寻找合理的灌水技术要素组合费时费力，为此人们提出了很多数学模型用于沟灌系统的设计和管理，其中一些灌溉模型已经被开发成应用程序，例如WinSRFR［3］和SIRMOD［4］。数学模型模拟可以为用户采用适宜的灌溉系统设计方案、评价灌溉系统性能提供有效手段，以达到提高灌溉质量的目的［5］。

入渗量估计是沟灌水流模拟研究中的重要问题之一。只有对入渗进行准确的估计，才能正确地描述灌溉过程中水分的运动，对灌水效果做出合理的评价。现有的沟灌模型大多采用经验公式估计入渗量，经验公式具有计算简单，参数较少等优点。然而在实际沟灌过程中，沟中水深和湿周不断变化，影响累积入渗量大小［6］，由于经验公式往往没考虑土壤的水力特性、水深和湿周变化等因素的影响，导致入渗量的估计出现较大偏差［7］。

随着对入渗机理的深入认识，人们提出了很多基于物理过程的沟灌入渗模型。例如Wöhling等［8］通过一个形状转换公式将沟灌二维入渗描述成一系列一维入渗的累加，该模型具有较高的精度，但是当计算节点较多时，模型计算效率较低。Warrick等［9］提出一个沟灌近似入渗模型，将沟灌二维入渗看成一维入渗和边界效应之和，并通过数值试验验证了模型，但此模型仅考虑了积水深度恒定的情况，与实际的沟灌过程中积水深度变化的情况有较大差异。Bautista等［10］通过对Warrick模型改进，使其可以应用于积水深度变化条件下的入渗计算，该模型只包含一个经验参数γ，计算较为简单。Warrick等［9］的研究表明，γ与土壤水力参数、积水深度和初始有效含水率有关。Bautista等［10］的研究表明，在定水头条件下γ值与积水深度有关，在变水头条件下γ值可取为常数。

目前关于参数γ的研究还只是定性地分析了其与影响因素之间的关系，并给出γ的取值范围，尚未提出参数γ的定量估计方法。在实际中，土壤的湿润程度、土壤水力特性和积水深度在灌水过程中随着时空变化，导致γ的取值具有时空变化特征，若将γ视为常数，则可能导致入渗计算的不准确，同时参数γ时空变化增加了其估计的难度。

近年来，人工智能技术，如人工神经网络、遗传算法和基因表达式编程（GEP）算法等被引入水文与水资源学领域，并被广泛应用于模型参数优化中。例如，Valipour等［11］使用遗传算法优化修正Kostiakov入渗模型参数，鲁帆等［12］采用多智能体遗传算法估计了马斯京根模型参数，彭昱忠等［13］使用GEP算法获得了单一重现期暴雨强度计算模型的参数。GEP算法是一种通用的自适应随机搜索算法，能够在缺乏先验知识的情况下，依赖实验数据的挖掘建立较为准确的预测预报公式。与传统的遗传算法等相比，GEP算法运算更加灵活，计算效率也更高［14］。

本文采用GEP算法，建立γ与其敏感因子之间的显式表达式，为沟灌入渗模型提供了有效的参数估计方法，并通过比较沟灌入渗模型与HYDRUS-2D计算结果，检验采用GEP算法估计γ方法的精度。

2 理论与方法

2.1 沟灌入渗模型 Bautista等［10］提出的沟灌入渗模型表达如下：

式中：I2D为单位沟长的累积入渗量，cm2；I1D为一维累积入渗量，cm；t为时间，min；W为湿周，cm；θS、θ0分别为饱和含水率和初始含水率，cm3/cm3；S为土壤吸湿系数，cm/min0.5；γ为经验参数。

因为积水深度沿湿周变化，计算I1D时使用的积水深度应该小于实际的积水深度。Bautista等［15］指出可使用湿周平均水深代替实际的积水深度，湿周平均水深可采用下式计算：

式中：hW为湿周平均水深，cm；h为积水深度，cm；z（x）为湿周节点上的垂向坐标，cm。

hW也用于计算土壤吸湿系数：

式中：KS为饱和导水率，cm/min；hf为土壤湿润锋处的压力水头，cm，可以通过Neuman公式计算［16］：

式中：h0为初始含水率对应的压力水头，cm；K（h）为导水率，cm/min。

整理式（1）可得γ的表达式：

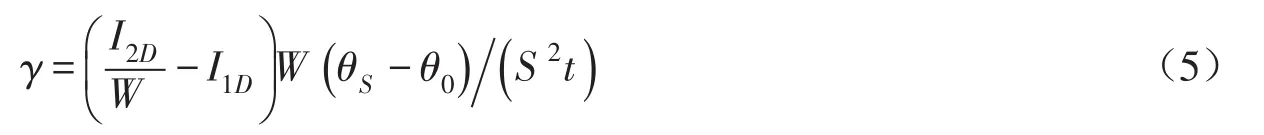
2.2 参数γ估计的GEP算法

2.2.1 数据集合 使用GEP算法时，首先需要建立GEP算法的有效数据集合，本研究中通过数值试验获得有效数据集合。选择了6种类型土壤进行数值试验，代表不同的土壤质地。对于每种土壤，模拟了不同沟截面形状、积水深度和初始含水率条件下的入渗，根据式（5）计算出不同模拟情景下的γ值。表1总结了不同模拟情景的土壤水力特性、积水深度和沟截面形状。沟截面形状及尺寸见图1。

式（5）中的二维和一维入渗量分别通过HY⁃DRUS-2D［17］和 HYDRUS-1D［19］计算得到。图 2 给出了HYDRUS-2D的计算区域。模型的上边界为定水头边界，根据积水深度设置；下边界条件为自由排水边界；其余边界为零通量边界；初始条件为初始含水率对应的压力水头。HYDRUS-1D计算区域为200 cm深的土壤剖面，上边界条件为定水头边界，根据湿周平均水深设置；下边界条件为自由排水边界；初始条件为初始含水率对应的压力水头。将计算的二维和一维入渗量代入式（5），进而获得不同模拟情景下的γ值。

表1 不同模拟情景的土壤水力特性、积水深度和沟截面形状

图1 沟截面形状及尺寸（单位：cm）

图2 HYDRUS-2D计算区域（单位：cm）

表2 数据集合统计指标

根据数值试验得到的162数据点，以饱和导水率Ks、积水深度h、有效含水率Θ（Θ=（θ0-θr）/（θS-θr））、进气值参数α、孔径分布指数n、沟深D和沟顶宽B作为输入变量，γ作为输出变量，建立GEP算法的有效数据集合，数据集合的统计指标见表2。将有效数据集合随机分成训练集合（70%）和验证集合（30%），训练集合包含112个数据点，用于GEP算法的运算；验证集合包含50个数据点，用于检验GEP算法的预测效果。

2.2.2 输入因子 分析γ的敏感参数，确定GEP算法的输入因子。分析的参数包括KS、Θ、α、n、h、D和B。以壤土和G2沟截面形状为基准，初始参数设置如下：KS=0.0173cm/min、α=0.036cm-1、n=1.56、Θ=0.49、h=10 cm、D=40 cm、B=20 cm。将所有的参数以10%的间隔从-50%增加到+50%，根据γ的变化情况确定GEP算法的输入因子。

设置不同的输入因子组合，比较不同组合GEP算法的预测效果，确定最优组合，建立γ的显式表达式。使用决定系数（R2）、均方根误差（RMSE）、平均绝对误差（MAE）和平均相对误差（MRE）作为评价指标，其计算方法如下：

式中：Oi和Pi为实测值和预测值；和为实测和预测值的平均值；n为比较变量的数量。

2.2.3 GEP算法过程 这里对参数估计的GEP算法过程的步骤进行简要总结，详细的介绍请参考Ferreira［11］。算法的主要步骤如下：（1）初始参数设置，包括适应度函数选择、终点集和函数集选择、染色体结构选择、连接函数选择、遗传算子及其相应的发生概率选择等；（2）根据遗传算子对当前种群进行遗传操作；（3）染色体解码，评价当前种群的适应度；（4）根据终止准则判断是否迭代，若不满足终止准则，生成新的种群，代数加一；若满足终止准则，停止计算。

重复（2）—（4）步骤达到预先指定的代数或找到一个最优解，停止计算。本研究中，使用GeneXpro程序进行GEP算法计算，GEP算法的主要参数设置见表3。

2.3 变积水深度条件入渗计算 将建立的γ显式表达式应用于沟灌入渗模型，计算变积水深度条件下的累积入渗量并与HYDRUS-2D计算结果比较，检验GEP算法对γ的估计精度。在计算中，沟中间位置截面的积水深度变化采用零惯量模型和Bautista入渗模型耦合的沟灌水流模拟模型得到，作为入渗模型的上边界条件。模型的输入参数见表4，结果如图3所示。采用MRE和RMSE评价沟灌入渗模型的效果。

图3 灌水沟中间位置截面的积水深度变化

3 结果分析与讨论

3.1γ的敏感分析 图4给出了γ对参数变化的响应结果，可以看出，γ对积水深度最敏感，壤土条件下γ随着积水深度的增大而减小。需要注意的是，γ与积水深度之间并不存在确定的正相关关系，还受土壤类型等因素的影响。Warrick等［20］的研究表明，砂壤土条件下γ随积水深度增大而增大，粉质壤土条件下γ随积水深度增大而减小。由图4可知γ对有效含水率和沟深也很敏感，这与Warrick等［9］的研究结果一致。γ随着饱和含水率、进气值参数和孔径分布指数的变化在-10%～10%范围内波动（图4），表明γ对土壤水力特性参数也较为敏感，这与Bautista等［15］的研究结果一致。

表3 GEP算法参数设置

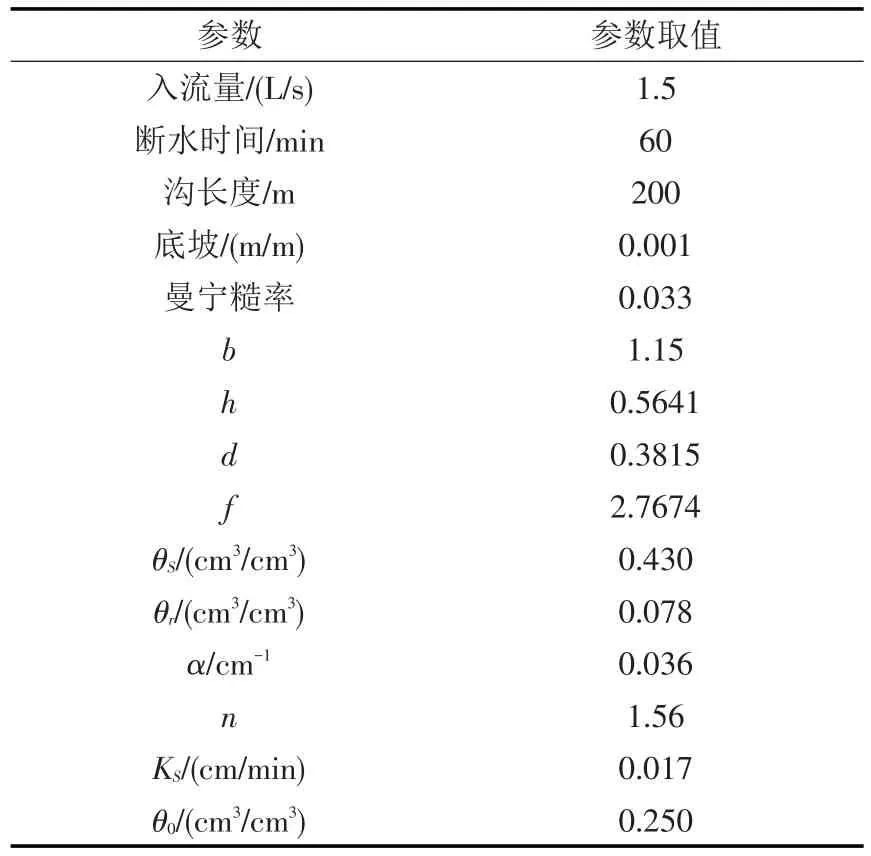
表4 模型输入参数

图4 γ对各参数变化的敏感性分析

参数γ主要用于重力对入渗边界影响的修正，以及土壤剖面含水量分布和吸湿系数近似处理可能产生误差的修正［22］。由于积水深度和沟截面形状决定入渗边界的范围，因此γ对积水深度和沟截面形状最敏感。土壤有效含水率、导水率、进气值参数和孔径分布指数影响土壤剖面含水量分布情况和吸湿系数的大小，因此γ对土壤有效含水率和土壤水力特性参数也较为敏感。

3.2 最优输入因子组合 根据γ的敏感性分析结果选择h、Θ、D、KS、α和n作为GEP算法的输入因子，并设置5组输入因子组合方案。表5给出了不同方案的GEP算法对γ预测效果的评价结果。由表5可知，方案1中仅使用γ的三个最敏感参数Θ、h和D，γ的预测精度较低。方案2、3、4在方案1的基础上分别增加了参数KS、n和α，与方案1相比，方案2、3、4的γ预测精度都有所提高，这表明土壤水力特性参数对γ有较大的影响。Bautista等［15］指出，与积水深度相比，土壤类型对γ的影响更加显著，因此将土壤水力特性参数作为输入因子可以有效地提高GEP算法对γ的预测精度。与方案2相比，方案3、4的预测精度更高，训练组的R2值分别为0.825和0.775，这表明与饱和导水率相比，孔径分布指数和进气值参数对γ的贡献更大。

由表5可知，方案3在训练组中的预测效果较好，R2值最高，但是在验证组预测精度较低，R2值仅为0.576。方案5在训练和验证组的预测效果均较好，MAE值最小，分别为0.053 cm2和0.049 cm2。由于方案5考虑的影响因素最全面，预测效果较好（见图5），因此确定方案5为最优的输入因子组合。最优输入因子组合GEP算法得到的γ表达式为：

表5 不同输入因子组合的GEP算法对γ预测效果评价指标

图5 方案5实测值和GEP算法预测值之间的回归分析

3.3 变积水深度条件下γ的估计值 图6给出了变积水深度条件下不同土壤类型采用GEP算法估计的γ值。可以看出γ随着积水深度增加，最终稳定在一个恒定值附近。这是由于在一定时间后积水深度变化不大（图3），此时的入渗过程可视为定积水深度条件下的入渗，因此γ值稳定在恒定值附近。对于不同类型的土壤，γ随着土壤导水率增加而增加，黏壤土的γ值为0.82，砂土的γ值为1.13。这与Bautista等的结果一致，其研究结果表明质地较粗的土壤的γ值更大。Bautista等给出的黏壤土、砂黏壤土和壤砂土的γ值分别为0.8、0.9和1.0［10］，本研究中估计的3种土的γ稳定值分别为0.82、0.88和1.12，与Bautista等的结果相近，表明GEP算法对γ的估计效果较好。

3.4 变积水深度条件下累积入渗量 将式（10）应用于沟灌入渗模型计算累积入渗量，并与HYDRUS-2D计算的“精确”结果进行比较，结果如图7所示。从图中可以看出，采用GEP算法估计γ值的沟灌入渗模型计算精度较高，MRE值均小于5%，满足入渗计算的精度要求，这表明所建立的基因表达式（式（10））在变积水深条件下对γ的估计效果较好。

为了进一步研究变积水深度对γ的影响，通过拟合沟灌入渗模型计算的累积入渗量与HYDRUS-2D计算的“精确”结果，反求出变积水深度的γ值，并与定积水深度的γ值进行比较（见表6），结果表明变积水深度的γ值与定积水深度的γ值取值接近，这与Bautista等的结果一致，其研究发现变积水深度和定积水深度的γ值相近［10］，这表明γ对积水深度变化条件不敏感。虽然基因表达式（式（10））是基于定积水深度条件建立的，在变积水深度条件下对γ的估计效果也较好。GEP算法估计的γ稳定值与反求的变积水深度的γ值接近（见表6），因此使用估计的γ稳定值计算沟灌累积入渗量，在满足计算精度要求的同时，可以使沟灌入渗模型的应用更加方便。

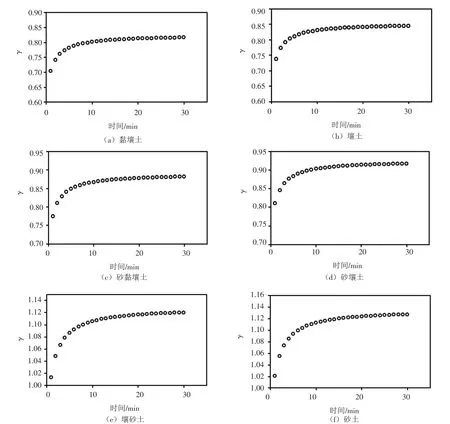
图6 变积水深度条件下不同类型土壤采用GEP算法估计的γ值

表6 变积水深度和定积水深度条件的γ值

3.5 土壤类型对边界效应的影响 为了研究土壤类型对边界效应的影响，本文模拟了不同土壤在定积水深度（10 cm）和相同初始土壤含水率（0.25）条件下的入渗。入渗过程中与一维累积入渗量增加速率相比，总入渗量增加速率更大，因此入渗过程中边界效应对总入渗量的贡献逐渐增大（见图8）。这是在入渗边界中考虑了水流重力作用影响的结果［21］，在入渗开始阶段，土壤基质势起主导作用，随着入渗时间的推进，土壤含水率增加，毛管基质势作用逐渐减小，重力势的作用逐渐增大，因此边界效应对总入渗量贡献逐渐增大。由图9可知对于质地较粗的土壤，边界效应对总入渗量贡献更大，黏壤土中边界效应的最终贡献约为25%，砂土中约为37%。这是由于粗质土壤的砂粒含量较多，对水分的吸附能力小，重力对水分运动的影响大，进而导致边界效应对总入渗量的贡献较大。

图7 采用GEP算法估计γ值的沟灌入渗模型计算的入渗量与HYDRUS-2D计算结果比较

图8 砂壤土总入渗量和一维累积入渗量模拟结果

图9 入渗过程中边界效应对总入渗量贡献

4 结论

本文采用基因表达式编程算法，建立了沟灌入渗模型参数γ与最优组合因子之间的基因表达式，提出了参数γ的估计方法，并分析了变积水深度对γ值和累积入渗量影响以及土壤类型对边界效应的影响。主要结论如下：

（1）γ与积水深度、沟形状和土壤水力特性等因素有关，其中γ对积水深度、初始有效含水率和沟深度最敏感，建立的基因表达式为γ与积水深度、初始有效含水率、沟深、饱和导水率和进气值参数之间的定量关系。

（2）变积水深度的γ值与定积水深度的γ值取值接近，基于定积水深度条件建立的基因表达式在变积水深度条件下对γ的估计效果较好，与利用HYDRUS-2D模型计算得到的“精确”入渗量相比，应用基于γ估计值的沟灌入渗模型计算的累积入渗量误差小于5%，满足计算精度要求。对于质地较粗的土壤，γ值更大，黏壤土γ值约为0.8，砂土的γ值约为1.2。

（3）入渗过程中受重力作用的影响，边界效应对总入渗量的贡献逐渐增大。与细质土壤相比，粗质土壤中边界效应对总入渗量的贡献更大，本研究条件下，黏壤土中边界效应最终贡献约为25%，砂土中约为37%。

参 考 文 献：

［1］ ESFANDIARI M，MAHESHWARI B L.Field evaluation of furrow irrigation models［J］.Journal of Agricultural Engineering Research，2001，79（4）：459-479.

［2］ WALKER W R，SKOGERBOE G V.Surface Irrigation：Theory and Practice［M］.Prentice-Hall Inc，Englewood Cliffs，N.J.，1987.

［3］ BAUTISTA E，CLEMMENS A J，STRELKOFF T S，et al.Modern analysis of surface irrigation systems with WINSRFR［J］.Agricultural Water Management，2009，96：1146-1154.

［4］ WALKER W R.SIRMOD III—Surface Irrigation Simulation，Evaluation and Design：User’s Guide and Techni⁃cal Documentation［M］.Dept.of Biological and Irrigation Engineering，Utah State Univ.，Logan，Utah.2003.

［5］ 许迪，李益农.精细地面灌溉技术体系及其研究的进展［J］.水利学报，2007，38（5）：529-537.

［6］ 刘亶仁，路京选.沟灌二维入渗条件下累计入渗量变化规律的研究［J］.水利学报，1989（4）：11-21.

［7］ ZERIHUN D，FURMAN A，WARRICK A W，et al.Coupled surface-subsurface flow model for improved basin irrigation management［J］.Journal of Irrigation and Drainage Engineering，2005，131（2）：111-128.

［8］ WÖHLING T H，SCHMITZ G H，MAIHOL J C.Modeling two-dimensional infiltration from irrigation furrows［J］.Journal of Irrigation and Drainage Engineering，2004，130（4）：296-303.

［9］ WARRICK A W，LAZAROVITCH N，FURMAN A，et al.Explicit infiltration function for furrows［J］.Journal of Irrigation and Drainage Engineering，2007，133（4）：307-313.

［10］ BAUTISTA E，WARRICK A W，SCHLEGEL J L，et al.Approximate furrow infiltration model for time-variable ponding depth［J］.Journal of Irrigation and Drainage Engineering，2016，04016045.

［11］ VALIPOUR M，MONTAZAR A A.Optimize of all effective infiltration parameters in furrow irrigation using visual basic and genetic algorithm programming［J］.Australian Journal of Basic and Applied Sciences，2012，6（6）：132-137.

［12］ 鲁帆，蒋云钟，王浩，等.多智能体遗传算法用于马斯京根模型参数估计［J］.水利学报，2007，38（3）：289-294.

［13］ 彭昱忠，元昌安，林开平，等.暴雨强度计算模型参数拟合优化的新进化方法［J］.广西大学学报：自然科学版，2013，38（5）：1173-1178.

［14］ FERREIRA C.Gene expression programming：a new adaptive algorithm for solving problems［J］.Complex Sys⁃tems，2001，13（2）：87-129.

［15］ BAUTISTA E，WARRICK A W，STRELKOFF T S.New results for an approximate method for calculating two-di⁃mensional furrow infiltration［J］.Journal of Irrigation and Drainage Engineering，2014，140（10）：349-356.

［16］NEUMAN S P.Wetting front pressure head in the infiltration model of Green and Ampt［J］.Water Resources Re⁃search，1976，12（3）：564-566.

［17］ ŠIMŮNEK J，ŠEJNA M，van GENUCHTEN M Th.The Hydrus-2D software package for simulating water flow and solute transport in two-dimensional variably saturated media，Version 1.0，IGWMC-TPS-53［Z］.Interna⁃tional Ground Water Modeling Center，Colorado School of Mines，Golden，Colo.1996.

［18］ HILLS R G，PORRO I，HUDSON D B，et al.Modeling one-dimensional infiltration into very dry soils.1.Model development and evaluation［J］.Water Resources Research，1989，25（6）：1259-1269.

［19］ ŠIMŮNEK J，ŠEJNA M，van GENUCHTEN M Th.HYDRUS 1D software package for simulating the one-dimen⁃sional movement of water heat and multiple solutes in variably saturated media，version 2.0［Z］.International Ground Water Modeling Center，Colorado School of Mines，Golden，Colo.1998.

［20］ WARRICK A W，LAZAROVITCH N.Infiltration from a strip source［J］.Water Resources Research，2007，43，W03420.

［21］ HAVERKAMP R，ROSS P J，SMETTEM K R J，et al.Three-dimensional analysis of infiltration from the disc in⁃filtrometer 2.Physically based infiltration equation［J］.Water Resources Research，1994，30（11）：2931-2935.