高含沙泄洪水流的荷载特性试验研究

练继建，杜昀怡，刘 昉，胡剑超

（天津大学 水利工程仿真与安全国家重点实验室，天津 300072）

1 研究背景

我国黄河流域多年平均含沙量在汛期可达300 kg/m3。当水流中的泥沙颗粒，特别是其中的黏性（即d＜0.01 mm，d为泥沙粒径）泥沙颗粒，所占比重达到某一程度而使含沙水流整体的物理特性、运动特性以及输沙特性等不再符合牛顿流体运动学规律时，即可将其称为高含沙水流，亦可称为宾汉流体［1］。高含沙水流内部的黏性泥沙颗粒在运动过程中相互碰撞产生大量的絮网结构，水流的黏性系数将发生明显的变化，产生宾汉极限剪切力，进而对水流的荷载特性产生影响［2］。高含沙水流一般属于由水和中性悬浮质组成的固液两相流。两相流中泥沙颗粒运动所需能量主要由水流紊动能所提供，泥沙颗粒的运动会反作用于水流，两者相互制约与影响。由于泥沙颗粒运动的随机性和复杂性，其运动学规律难以预测和计算，关于挟沙水流与清水相比其紊动是增强了还是减弱了目前学术界尚未达成共识，并且国内外的相关研究主要集中于河道中的高含沙渐变水流，而关于高含沙泄洪水流的研究还较少。

针对含沙水流荷载特性的研究大致形成三类意见。其中Bagnold［3］通过进行轻质沙水槽试验认为泥沙的存在将抑制水流的紊动，紊动强度随含沙量的增加而逐渐减小；王兆印等［4］通过研究大雷诺数非牛顿体明渠流发现紊动中的高频分量消失而低频分量增加，含沙水流紊动强度大幅低于清水。而Muller［5］的水槽试验结果却表明水流中的泥沙颗粒将加剧流体内部的紊动程度，含沙水流的脉动强度显著大于清水；李丹勋等［6］从简化的颗粒运动方程出发分析泥沙颗粒脉动与水流脉动之间的关系，同样认为泥沙颗粒在顺水流方向与垂直于水流运动方向上的脉动强度均大于清水；文献［7-9］也得出了相似的结论。而陈立等［10-12］通过对紊流机理的分析认为泥沙颗粒对水流的紊动既有促进又有抑制的作用，与含沙量、流速和颗粒粒径等因素均有关，并且应用MicroADV研究了流速条件对含沙水流紊动结构的影响，认为流速条件是决定含沙量与紊动强度关系的重要因素；Bohlen［13］通过水槽试验模拟河道内含沙水流的过流情况，认为水流紊动强度与含沙量之间的关系与水流分区有关，其中主流区水流在含沙量较小时脉动强度大于清水，而全流域范围内水流的脉动强度在含沙量较大时均大于清水。以上学者的研究表明，高含沙渐变流的荷载特性已研究较为充分，而高含沙泄洪急变水流的荷载特性尚需研究。孔板作为常见的消能工可有效增强水流的紊动程度形成急变水流。泥沙颗粒影响水流紊动的方式有多种，本文主要通过变化挟沙条件（含沙量）与水流条件（流速），研究高含沙泄洪水流的荷载特性。

2 模型试验概况

2.1 模型简介 模型试验系统主要由孔板、电磁流量计和管道泵三个部分组成，并由内径130 mm的灰塑料管连接，形成一个自循环系统，并通过管道泵下游处的蝶阀控制流量，如图1所示。为增强试验系统中水流的紊动强度，在流道内适宜位置处设置孔板。孔板孔径比（d/D）为0.692（90/130），d为孔口直径，D为管道内径。管道内流量由电磁流量计测量，水流循环所需动力由管道泵提供（设减震垫并采用软连接）。孔板试验段顺水流方向沿底部中线布置11个测点，其中1#至2#测点位于孔板前，3#至11#测点位于孔板后。1#测点距孔板上游19.5 cm（1.5D），2#测点距孔板上游6.5 cm（0.5D），3#测点位于孔板下游处1 cm，3#至9#测点段各测点间隔6.5 cm（0.5D），9#至11#测点段各测点间隔13 cm（1.0D），如图2所示。

图1 模型试验系统

图2 测点布置（单位：cm）

2.2 试验工况 为研究含沙量的差异对荷载特性的影响，共配置包括清水在内7种不同含沙量的水体作为试验对象，分别为0（清水）、50 kg/m3、 100 kg/m3、 150 kg/m3、 200 kg/m3、250 kg/m3和300 kg/m3。通过改变管道泵后蝶阀的开度，调整并控制流量，研究流速条件的变化对荷载特性的影响。当流量为178 m3/h、168 m3/h、144 m3/h和85 m3/h时，管道内相应流速分别为3.73 m/s、3.52 m/s、3.02 m/s和1.78 m/s。共进行了28组不同工况的含沙水流模型试验，如表1所示。经计算本试验所有工况条件下最小雷诺数均大于15 000，根据含沙量与水流过流能力间关系的研究成果［14-16］，试验在蝶阀开度相同时，含沙量的改变对过流能力的影响可忽略不计。试验用沙为细黄土，中值粒径及粒径级配如表2及图3所示。

表1 试验工况

表2 试验用沙粒径级配

3 时均压力

3.1 沿程分布规律 时均压力由流道内的静水压力与因水流运动而引起的动水压力两部分组成，是反应水流荷载特性的重要参数。不同流速条件下各含沙量水流时均压力的沿程分布情况如图4至图7所示。横坐标x/L为测点在试验段的相对位置（x为该测点距第一个测点的距离，L为试验段总长度），纵坐标为时均压力值（9.8 kPa）。由试验结果可知：高含沙泄洪水流的时均压力沿程分布具有明显的规律性，且与清水的分布规律相同，幅值大小随含沙量的增加而增加。

图3 粒径级配曲线

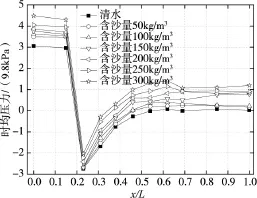
图4 流速3.73 m/s时均压力沿程分布

图5 流速3.52 m/s时均压力沿程分布

图6 流速3.02 m/s时均压力沿程分布

图7 流速1.78 m/s时均压力沿程分布

图8为根据预试验得出的孔板处紊流示意图。分析孔板前后流态可知，孔板前的水流平稳段，1#测点与2#测点的时均压力值接近，在水流越过孔板后，流线突变产生漩涡区造成负压，孔板后的3#测点取得负压最大值，此后水流逐渐恢复平稳，水流旋滚减弱，负压逐渐减小并恢复至正压。对比不同流速条件的试验结果可知，时均负压的大小与管道流速的大小相关，流速减小时负压也逐渐减小，试验中最小流速工况下负压已消失。

图9为含沙量与时均压力（负压）最大值之间的关系。其中横坐标为含沙量（kg/m3），纵坐标为时均压力最大值（9.8 kPa）。由试验结果可知：流速一定时，泄洪急变水流的时均压力荷载特性与水流含沙量有关，其中流速3.72 m/s、含沙量300 kg/m3的水流，时均压力峰值相较于同流量清水而言增加26.09%；而流速降低至3.52 m/s、3.02 m/s和1.78 m/s时，增幅分别为46.36%、170.21%和178.10%，可以看出增幅也在逐渐增大。试验含沙量范围内，高含沙水流的时均压力幅值大小随含沙量的增加而持续增加。

图8 管道孔板处紊流负压示意图

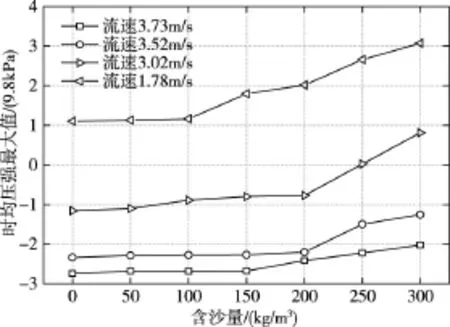
图9 时均压力最大值与含沙量的关系

4 脉动压力

4.1 沿程分布规律 由紊流力学理论可知，过流边壁上的脉动压力是由水流运动时内部存在的漩涡紊动产生的，因此可以说漩涡的存在是脉动压力产生的必要前提，其运动特征决定了脉动压力的特征。孔板的特殊体型使经过的水流先收缩再扩散，在突变的流动边界上，由于水流不断的分离和扩散，其内部将形成大量不同尺度和形态的漩涡，因此孔板后的脉动压力一般较大。

标准差σv可以有效表征任意随机变量偏离其平均值的程度，因此工程上常采用脉动压力的标准差来表征水流紊动的强度，如下式所示：

式中：为变量v在采样时间段内的平均值；v′为该瞬时的脉动量。

不同流速条件下各含沙量水流脉动压力的沿程分布情况如图10至图13所示。横坐标x/L为测点在试验段的相对位置（x为该测点距第一个测点的距离，L为试验段总长度），纵坐标为脉动压力值（9.8 kPa）。

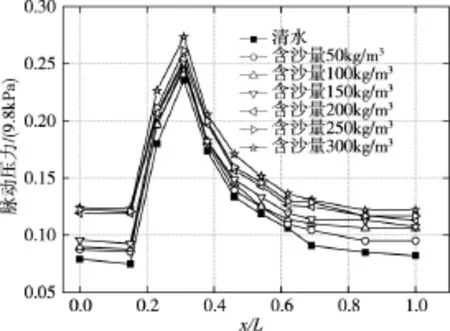
图10 流速3.73 m/s脉动压力沿程分布

图11 流速3.52 m/s脉动压力沿程分布

图12 流速3.02 m/s脉动压力沿程分布

图13 流速1.78 m/s脉动压力沿程分布

由试验结果可知：高含沙泄洪水流的脉动压力沿程分布具有明显的规律性，且与清水的分布规律相同。水流在孔板前1#测点与2#测点的脉动强度较小，从靠近孔板位置处（孔板前0.5D）开始，脉动强度迅速增加，并在孔板后0.5D处取得脉动压力最大值，在沿程分布图中表现为明显的“峰”，而后水流脉动强度逐渐降低，并在孔板后2.5D处逐渐趋于平稳。对比上述4种不同流速条件的试验结果可知：流速条件越强，其脉动压力形成的“峰”越为尖锐；而流速条件越弱，其脉动压力形成的“峰”越为圆滑。

图14为含沙量与脉动压力最大值之间的关系。其中横坐标为含沙量（kg/m3），纵坐标为脉动压力最大值（9.8 kpa）。由图可知：脉动压力幅值大小受含沙量和流速条件的双重影响。流速条件较弱时（图14下部两条曲线），脉动压力幅值随含沙量的增加而先增加后减小。其中流速3.02 m/s的水流，脉动压力在含沙量上升至300 kg/m3后，其幅值整体下降，峰值相较于含沙量250 kg/m3的水流降低10.19%；流速1.78 m/s的水流脉动压力在含沙量上升至250 kg/m3后，其幅值整体下降，峰值相较于含沙量200 kg/m3的水流降低17.54%。而流速条件较强时（图14上部两条曲线），试验含沙量范围内，脉动压力幅值随含沙量的增加而持续增加。其中流速3.73 m/s、含沙量300 kg/m3的水流，脉动压力峰值相较于同流速清水而言增加15.95%；流速3.52 m/s的水流相应增幅可达19.49%。并且由上述试验数据可推断，若含沙量继续增加，流速3.53 m/s和流速3.73 m/s的试验曲线也将出现拐点。

图14 脉动压力最大值与含沙量的关系

这是因为流速条件较强时，泥沙颗粒从水流中获得充足的能量，紊动相对充分，而含沙量的增加使水流整体的动能和势能增加，因此脉动压力幅值随含沙量的增加而持续增加；而流速条件较弱时，含沙量较高的水流所携带的能量不足以维持全部泥沙颗粒的运动，部分泥沙颗粒受重力作用而下沉，并且随含沙量的增加，水流的黏滞系数也在不断增加，不利于絮网结构的发育，对紊动存在抑制作用，因此出现脉动压力在含沙量达到一定值后开始减小的现象。并且由试验中流速3.02 m/s的水流在含沙量250 kg/m3时出现脉动压力拐点，而流速1.78 m/s的水流在含沙量200 g/m3时就出现脉动压力拐点可以推断，高含沙泄洪水流脉动压力的拐点随含沙量的变化规律与流速条件呈正相关关系，即流速条件较强时拐点含沙量较大，而流速条件较弱时拐点含沙量较小。这与文献［17］中的观点，存在一个“临界含沙量”使得脉动压力不随含沙量的变化而呈线性变化的概念相通。并且若将试验中高流速条件水流类比为河道主流区水流而将低流速条件水流类比为河道近壁区水流，则得出的结论与陈立［10-11］和Bohlen［12］的结论一致。

由实际工程中泄洪水流的流速明显大于试验水流的流速可知，高含沙河流高坝泄洪水流中的泥沙颗粒一般可充分紊动，因此其脉动压力值随含沙量的增加而增加。由试验结果本文提出高含沙高坝泄洪水流的脉动压力修正方法，即挟沙水流的脉动压力值为相应清水脉动压力值与修正系数m间的乘积，含沙量范围为0～300 kg/m3时，m的取值范围为1～1.20，且含沙量越大m取值越大。

4.2 概率密度 由一个随机过程的概率密度函数可知该随机过程的行为特征。平稳随机过程的数学表达式很难获得，因此常通过研究其概率密度分布来描述该随机过程的行为特征。水流脉动压力概率密度分布的正态性是表征水流荷载特性的重要因素。可以通过计算其偏态系数CS和峰度系数CE来直观的判别其分布的正态性。偏态系数CS表征概率密度分布的对称性，峰度系数CE表征概率密度分布偏离标准正态的程度。偏态系数CS的计算过程如式（2）所示，峰度系数CE的计算过程如式（3）所示。CS=0、CE=3的分布属于标准正态分布。

式中：P为脉动压力瞬时值；为脉动压力平均值；σ为脉动压力标准差。

不同流速条件下各含沙量水流孔板后脉动压力峰值处的概率密度分布如图15至图18所示。其偏态系数CS及峰度系数CE如表3所示。

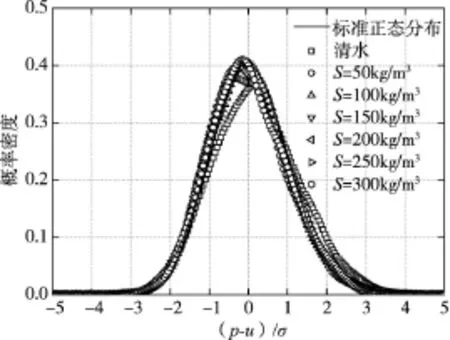
图15 流速3.73m/s脉动压力概率密度分布

图16 流速3.52m/s脉动压力概率密度分布

图17 流速3.02m/s脉动压力概率密度分布

图18 流速1.78m/s脉动压力概率密度分布

表3 脉动压力峰值处偏态系数与峰度系数

由试验结果可知，脉动压力峰值处测点在流速3.73 m/s的工况下其偏态系数CS在0.11～0.36之间，峰度系数CE在2.81～3.16之间；在流速3.52 m/s的工况下其偏态系数CS在0.12～0.35之间，峰度系数CE在2.70～3.21之间；在流速3.02 m/s的工况下其偏态系数CS在0.03～0.29之间，峰度系数CE在2.82～3.09之间；在流速1.78 m/s的工况下其偏态系数CS在-0.18～0.10之间，峰度系数CE在2.33～3.23之间。综合各工况试验结果可知，偏态系数集中在0的附近（-0.18～0.36之间），峰度系数集中在3的附近（2.33～3.23之间），因此可以认为脉动压力概率密度分布基本符合正态分布，并且含沙量和流速条件的改变对概率密度分布的影响不大，且变化不存在明显的规律性，这也符合脉动压力是水流作用下随机荷载的性质，泥沙颗粒的存在并未改变这一特性。

4.3 频谱特性 水工建筑物泄洪时所产生的脉动压力是由具有一定能量的频率分量组成的，而功率谱密度则表征了这些频率分量所具有的能量的平均值。不同流速条件下各含沙量水流孔板后脉动压力峰值处的功率谱密度如图19至图22所示，横坐标为频率的对数值。

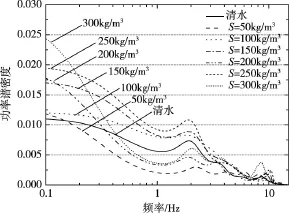
图19 流速3.73m/s脉动压力功率谱

图20 流速3.52m/s脉动压力功率谱

图21 流速3.02m/s脉动压力功率谱

图22 流速1.78m/s脉动压力功率谱

由试验结果可知：随流速条件的减弱，水流脉动频率分布范围逐渐减小，流速降至1.78 m/s时尤为明显。另外，相同流速条件的工况下，随含沙量的增加，脉动能量中低频分量明显增加。由紊流理论可知，水流紊动中的低频分量是由大尺度漩涡产生的，因此可以证明随含沙量的增加，紊动中的水流由于黏度的增加形成的低频大尺度漩涡数量明显增多，水流的紊动形式发生了变化。这与文献［4］以及文献［12，18］得出的结论相同。

5 结论

通过自主设计的模型试验，研究了高含沙泄洪水流在不同流速条件下的荷载特性，得出以下结论：（1）高含沙泄洪水流时均压力的沿程分布规律与清水相同，其幅值大小随含沙量的增加而增加。（2）高含沙泄洪水流脉动压力的沿程分布规律与清水相同，其幅值特性受含沙量与流速条件的双重影响，当流速条件较强时，脉动压力幅值随含沙量的增加而持续增加，而当流速条件较弱时，随含沙量的增加而先增加后减小；提出了实际工程中高含沙河流上高坝泄洪水流脉动压力计算的修正公式与适用范围。（3）高含沙泄洪水流脉动压力的概率密度分布基本符合正态分布，偏态系数CS集中在0的附近，峰度系数CE集中在3的附近，且分布不随含沙量和流速条件的变化而呈规律性变化趋势。（4）高含沙泄洪水流脉动压力的功率谱密度随流速条件的增加而逐渐增加，频带宽度变大，并且脉动的低频分量随含沙量的增加而增加。

参 考 文 献：

［1］ 张瑞瑾.河流泥沙动力学［M］.北京：中国水利水电出版社，1998.

［2］ 郑委，郭庆超，陆琴.高含沙水流基本理论综述［J］.泥沙研究，2011（2）：75-90.

［3］BAGNOLD R A.Some Flume Experiment on Large Grains but Litter Denser than Transporting Fluid and Their Im⁃plications［C］//Proc.，Inst.Civil Engrs.1955.

［4］ 王兆印，曾庆华，张新玉.非牛顿体固液两相流的试验研究［J］.泥沙研究，1990（3）：1-12.

［5］ MULLER A.Turbulence Measurements over a Movable Bed with Sediment Transport by Laser-Anemometry［C］//Proceedings of the Fifteenth Congress.1963.

［6］ 李丹勋，王兴奎，王殿常.流速梯度对悬浮颗粒脉动强度的影响［J］.泥沙研究，2000（3）：30-35.

［7］ TSUJI Y，MORIKAWA Y.LDV measurements of air-solid two-phase flow in a horizontal pipe［J］.J.Fluid Mech.，1982，120：385-409.

［8］ STEIMKE J L，DUKLER A E.Laser transport in a vertical turbulent boundary layer［J］.Int.J.Multiphase Flow，1983，9：751-754.

［9］ROGER C B，EATON J K.Partical transport in a vertical turbulent boundary layer［J］.Int.J.Multiphase Flow，1990，16：819-834.

［10］ 陈立，詹义正，李义天，等.泥沙对水流紊动影响的初步分析［C］//第二届全国泥沙基本理论研究学术讨论会论文集，北京：中国建材工业出版社，1995.

［11］ 陈立，林鹏，叶小云.泥沙对挟沙水流流动结构影响的研究［J］.水利学报，2003（9）：39-47.

［12］ 刘青泉，陈立.泥沙对水流的紊动的影响的进一步分析［J］.水利学报，1997（9）：77-82.

［13］ BOHLEN W F.Hotwire Anemometer A Study of Turbulence in Open Channel Flows Transporting Neutrally Buoy⁃ant Particles［R］.Experimental Sediment Technology Laboratory，1969.

［14］ 陈上群，罗荣华.高含沙水流对泄流能力影响的分析［J］.泥沙研究，1982（4）：67-75.

［15］ 陈立，王明甫.水流强度对高含沙水流流变参数影响的试验研究［J］.泥沙研究，1993（2）：57-66.

［16］ 赵文林.高含沙水流对泄流能力影响的研究概况［J］.人民黄河，1985（5）：20-25.

［17］ 柴炳钦，张连合，姚振华.双层泄流排沙孔门槽浑水脉动压力试验［J］.人民黄河，1988（6）：37-40.

［18］ 王德昌.浑水脉动压力试验研究［J］.人民黄河，1993（4）：33-36.