TATB基PBX界面热阻研究及导热系数预测

周筱雨, 杨雪梅, 韦兴文, 王 培

(中国工程物理研究院化工材料研究所, 四川 绵阳 621999)

1 引 言

高聚物粘结炸药(Polymer Bonded Explosive,PBX)是一种填充型聚合物基复合材料,由填充相(炸药晶体)及粘结剂基体组成。PBX制成的炸药部件是武器战斗部中重要的功能件和结构件。PBX本身为热的不良导体,由于热量不易导出, PBX部件在变温环境下由于内部存在较大的温差而易形成热应力,对部件的温度适应性造成重要影响[1,2]。

目前已知的填充型复合材料导热性能影响因素众多,如基体及填料的导热系数、体积百分比、填料颗粒的形状、粒径及粒径分布等。根据Willey小角衍射的结果[3],压制成型的PBX中炸药晶体/粘结剂界面的空隙尺寸一般为20 nm～2 μm,在此尺度下,空隙对流换热对界面传热的贡献很小,主要依靠接触面传热。由于炸药晶体与粘结剂的热膨胀系数存在较大差异,在PBX压制成型过程中,两相界面处往往会产生很多空隙和缺陷,炸药晶体/粘结剂界面的实际接触面积比名义界面积要低很多。实际上,炸药晶体/粘结剂的界面是由空隙及接触面组成的层状结构。TATB基PBX的实测导热系数远小于TATB晶体的导热系数[4-6]。根据Cornell R H[4]使用闪光法测定出TATB晶体的导热系数(0.80 W·m-1·K-1),以95%TATB为填充粒子、氟橡胶(0.19 W·m-1·K-1)为基体的PBX,使用适合于高填充率的海岛-网络模型计算得到的导热系数约为0.72 W·m-1·K-1,则远大于PBX实测值,这可能是没考虑界面热阻所致。考虑到界面热阻的影响,Hasselman[7]和Benvensite[8]等人在Maxwell两相模型的基础上进行了改进; Every[9]通过积分方法对Hasselman模型进行了进一步优化,使其在高颗粒填充率下的预测值与实测值更加接近; Wang[10]则同时考虑了填充粒子形状及界面热阻影响建立混合模型,弥补了Bruggeman模型[11]没引入界面热阻影响的缺点。这些模型虽然考虑了界面热阻,但距精确预测复合材料的导热系数还有一定距离,加之各种复合材料界面微观结构都很复杂,模型的预先假设与实际界面情况间还存在较大的差距,而且这些模型多建立在大量实验的经验或半经验模型,缺乏理论依据,应用时必须根据具体复合体系的界面参数,对模型进行修正,才能获得理想预测效果。因此,有必要针对界面热阻对复合材料的导热性能的影响开展深入研究,基于此,本研究通过理论计算和实验研究,获得高填充PBX中界面传热机制,并建立PBX导热系数预测模型,为高导热型PBX的配方设计提供指导。

2 实验部分

2.1 设计原理

固体与固体之间的接触,从亚微观的角度来看,仅仅发生在一些离散的接触面上,其余大部分为空隙或其他介质。有研究表明,即使两固体界面接触压力达到10 MPa,实际接触面积仍只占名义面积的1%～2%。界面的不完全接触处出现热流收缩,因而产生界面热阻。PBX中的主要组成相为炸药晶体和粘结剂,它们的热物理性能如线膨胀系数存在一个数量级的差距,因此在固化过程中,根据变形层理论,炸药晶体和粘结剂之间会形成一定厚度的界面(包含实际接触面和空隙等)。

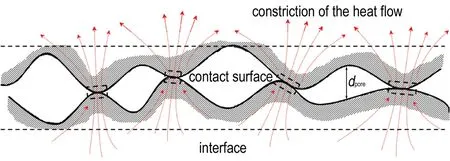
图1 PBX界面形态

Fig.1 Interface morphology of PBX

由于PBX为高填充率复合材料,炸药颗粒方向各异,界面分布状态非常复杂,因此,对于PBX整体界面热阻的研究具有相当难度。为了研究方便,通过制备如图2所示的单层界面样品以评估界面对热传导的综合阻滞作用。

图2 单层界面样品

Fig.2 Monolayer interface sample

2.2 实验设备

导热系数测试: 德国NETZSCH公司LFA447型激光导热仪; 界面层厚度检测: 美国HYSITRON公司TSI-0538型纳米压痕仪; 密度检测: 瑞士METTLER TOLEDO公司AX504型电子天平及密度仪; 粒径检测: 美国beckman coulter公司LS230型激光粒度仪; 形貌观测: 日本精工SPA300-HV型原子力显微镜。

2.3 样品制备

TATB粉末,晶体密度1.938 g·cm-3,粘结剂为氟橡胶,密度2.031 g·cm-3。采用冷压方法压制成尺寸为Φ12.7 mm×2 mm的TATB药片及同样规格的氟橡胶样品,测定两种样品的导热系数; 然后在TATB药片上涂覆氟橡胶,获得单层界面样品,并进行120 ℃热处理同时施加载荷2 h,使其界面状态与实际压制PBX中的界面相似。

3 结果与讨论

3.1 界面结构特性

通过激光衍射法对经筛选后TATB炸药晶体的粒径进行表征,其粒径数值服从数学期望μ为18.86的正态分布,如图3所示。

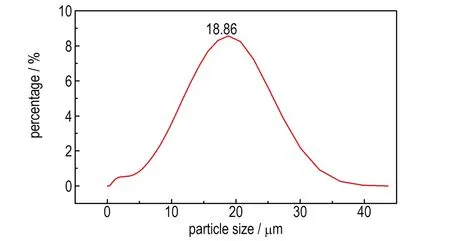
图3 TATB炸药晶体的粒径分布

Fig.3 Distribution of particle size of TATB explosive crystal

通过原子粒显微镜测试得到单质TATB药片粗糙度数据见表1。

表1 TATB药片表面粗糙度

Table 1 Surface roughness of TATB

scale/μmroughness/μmpeakvalue/μm10(6.37±1.34)×10-2(6.72±1.25)×10-15(5.52±1.49)×10-2(3.98±1.16)×10-11(5.59±0.92)×10-2(4.62±0.77)×10-1

通过多样品及多次测量的方式获取了多种尺度下的粗糙度及最大峰(谷)差值数据,可见TATB药片在大尺度(存在大量TATB晶体接触区域)及小尺度(TATB单晶表面)的视场范围内,粗糙度与最大峰(谷)差值等参数均无明显差异,说明TATB药片紧密压制后,其表面整体形貌与单个晶体相似,同时也可认为图2所示单层界面样品的设计是合理的。

使用密度仪对压制的单质TATB及粘结剂样品进行密度检测。其中TATB单质任选三个样品(以下简称TATB-1、TATB-2、TATB-3)的测试结果分别为: 1.867,1.881,1.866 g·cm-3,与理论值的比较结果如表2所示。

从表2可见,热压氟橡胶样品的压制密度与理论密度相当; 由于存在空隙,TATB晶体间压制密度与理论密度小于理论密度。

研究假定界面层是有一定体积及内容的实体,界面层由三种层状相结构组成,且力学性能在TATB/界面/氟橡胶中是连续的,即界面为TATB层与氟橡胶层之间力学性能的过渡层。使用纳米压痕仪检测界面样品的硬度数据如图4所示。

表2 单质样品密度

Table 2 Single component sample density

g·cm-3

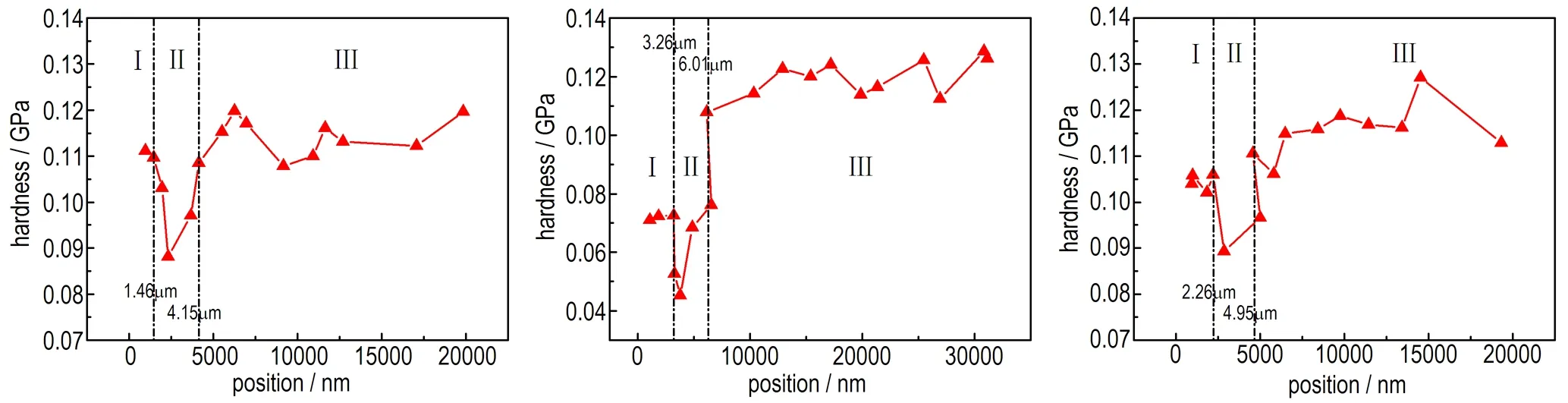
a. TATB-1 b. TATB-2 c. TATB-3

图4 不同压入深度的硬度值

Fig.4 Hardness of sample in each position

纳米压痕仪的压头由氟橡胶层开始压入,经由界面处压入TATB样品,三个样品的压痕数据均遵循相同的规律,即在Ⅰ区有一定的初始硬度,而在Ⅱ区则出现了明显的硬度下降,而在Ⅲ区硬度又迅速回升至原水平甚至增加。除了TATB及氟橡胶,由于界面层还存在大量空隙,所以界面力学性能会出现较明显变化。因此,可认为压入位置的Ⅰ区、Ⅱ区、Ⅲ区分别对应界面样品的氟橡胶层、界面层及TATB层。

3.2 界面热阻分析

因此,需要实验测定实际压制状态下TATB的导热系数,而不能采用文献值,同时,由于本研究所使用氟橡胶缺乏文献值,也需要对其导热系数进行测定,两种材料的导热系数测试结果见表3。

将上所述,单质TATB样品表面涂覆氟橡胶粘结剂,再次检测其导热系数,结果如图5所示。

由图5可见,含界面样品的导热系数明显下降,这主要是氟橡胶层及界面的综合作用所致。为分析界面的热阻滞效应,还应对氟橡胶带来的导热系数降低进行评估。

由于导热样品直径远大于厚度,因此可以认为只在样品轴向上有温度T的变化,即可以简化为一维传热过程,如图6。

表3 单质样品导热系数

Table 3 Coefficient of thermal conductivity of single component sample

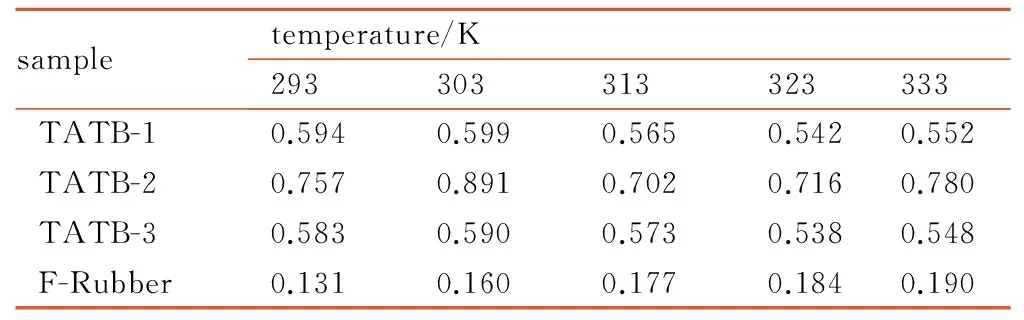
W·m-1·K-1

对于一维传热,在稳态条件下材料的导热系数根据傅里叶定律求得:

dQ=-k·ΔT·ds·dt

(1)

式中,dQ为在dt时间内通过垂直于ds方向上的热量 J;k为材料的导热系数,W·m-1·K-1; ΔT为垂直于ds方向上的温度梯度, K。

q1=q2=q3=qtotal

(2)

即:

(3)

解得:

(4)

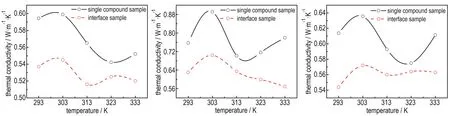
a. TATB-1 b. TATB-2 c. TATB-3

图5 单质及其界面样品导热系数

Fig.5 Thermal conductivity of interface sample

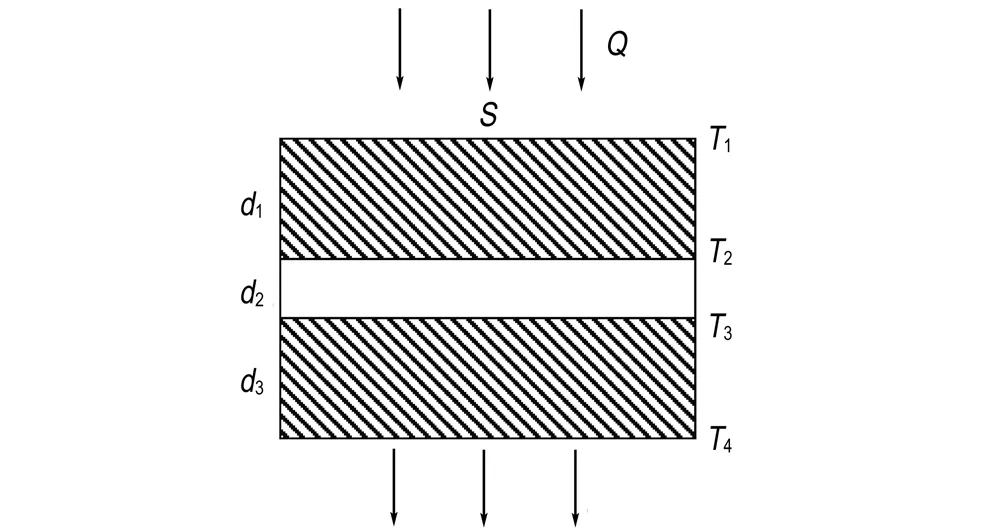
图6 多层样品传热示意图

Fig.6 Schematic diagram of heat transfer in multilayer samples

因此根据图4的硬度与压入深度的关系,推断出界面样品氟橡胶层及界面的厚度,并代入式4,计算得到TATB/氟橡胶粘接界面的导热系数,如表4所示。

表4 TATB/fluororubber界面导热系数

Table 4 Thermal conductivity of TATB/fluororubber Interfacial

temperature/Kthermalconductivity/W·m-1·K-1293(6.18±0.87)×10-3303(6.53±1.56)×10-3313(9.87±2.68)×10-3323(2.16±0.17)×10-2333(7.72±0.43)×10-3

界面导热系数代表TATB/氟橡胶/孔隙混合层状结构的综合导热性能,此类层状结构的热阻可用下式表示:

(5)

式中,di为实际PBX样品的界面厚度,m;ki为界面层导热系数, W·m-1·K-1。

3.3 TATB基PBX导热系数预测算例

研究对象为一种典型TATB基PBX。该PBX中TATB与氟橡胶的质量百分比为19∶1。由于TATB/氟橡胶实际接触面只在TATB表面积占有很小的比例。因此假设TATB晶体无缺陷,且PBX压制固化过程中由于TATB与粘结剂热膨胀系数不匹配,导致空隙均匀分布于TATB表面,从而可根据空隙率求出分布于TATB晶体表面空隙的实际厚度,即界面层的厚度。则不同空隙率、温度下的界面热阻与压制密度的关系如图7所示。

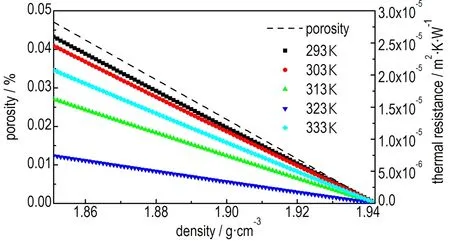
图7 密度与界面热阻的关系

Fig.7 The relationship between density and interfacial thermal resistance

在考虑填料的形状及界面热阻的情况下,PBX的导热系数模型表示如下[10]:

(6)

式中,λb为基体导热系数,W·m-1·K-1;λp为填充颗粒导热系数,W·m-1·K-1;λ为PBX导热系数,W·m-1·K-1;φp为填充颗粒体积百分比,%;α为界面影响因子;n为形状因子。

球形度的定义为与某凸面体体积相等的标准球形的表面积,与该凸面体的表面积之比。根据TATB晶胞参数:a=9.01 Å,b=9.03 Å,c=6.81 Å,α=108.59°,β=91.82°,γ=119.97°,及TATB的晶体形态[12],计算得到TATB理想晶体颗粒的球形度Φ约为0.784。

根据式(5),得到不同温度及密度下典型PBX的导热系数,与实测值的比较结果如图8所示。

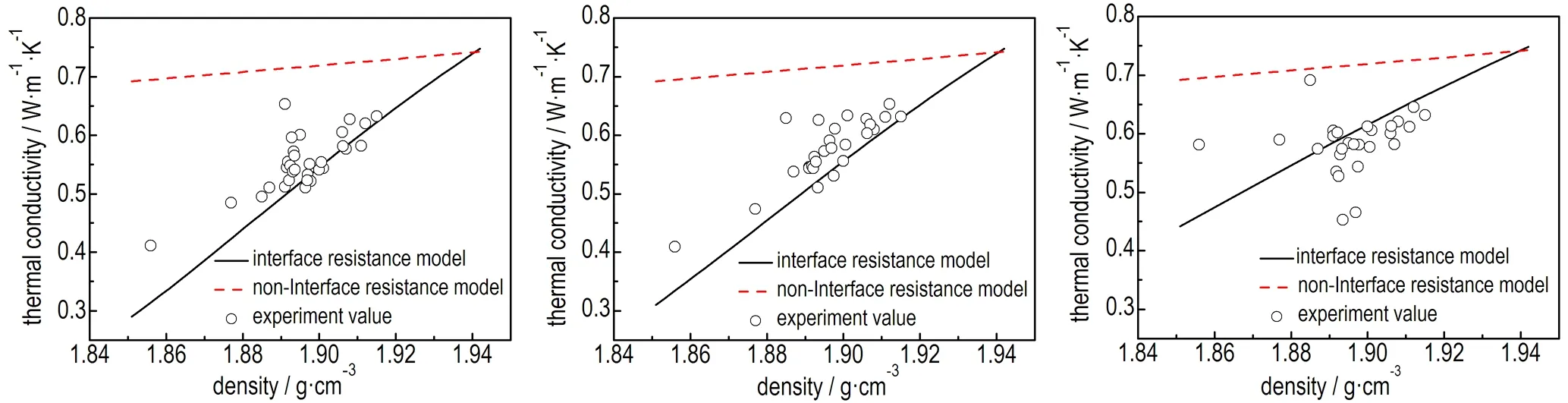
a. 293 K b. 303 K c. 313 K

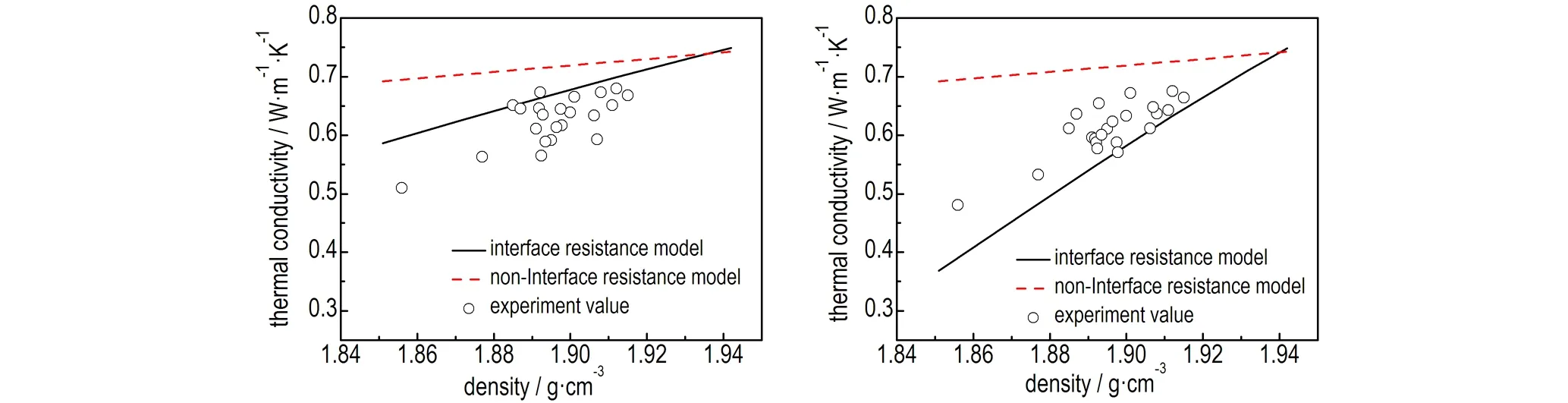
d. 323 K e. 333 K

图8 典型PBX导热系数计算值与实测值

Fig.8 Calculated value and measured value of thermal conductivity coefficient of typical PBX

图8中曲线分别代表含界面热阻及不含界面热阻的导热模型,对不同密度TATB基PBX导热系数的预测结果,可以看出在293～333 K下,引入界面热阻的模型对导热系数的预测结果更为准确,也更真实地反映了PBX材料实际的传热性能。

4 结 论

(1) 通过在单质TATB药片上涂覆粘结剂的方法,制备了单层界面样品。

(2) 采用纳米压痕、原子力显微等技术对样品表界面参数进行了表征,结合瞬态导热试验,计算出TATB/氟橡胶/空隙混合层状结构的导热系数。

(3) 最后将导热系数转换为界面热阻,引入至TATB基PBX的导热系数预测模型中,使某典型TATB基PBX的导热系数计算值与实测值表现出了很好的符合性。

研究证实了界面热阻在PBX热物理性能数值模拟中的重要性。在进一步的研究中可根据相应的试验手段,建立各类典型炸药晶体与粘结剂之间界面热阻数据库,为PBX炸药配方设计提供数据支持。

参考文献:

[1] 李敬明, 温梦萍, 黄毅民. 热循环对TATB基高聚物粘结炸药性能的影响研究[J].含能材料, 2005, 13(4): 208-210.

LI Jing-ming, WEN Mao-ping, HUANG Yi-min. Effect of thermal cycling test on the properties of TATB based PBX[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2005, 13(4): 208-210.

[2] 田勇, 张伟斌, 温茂萍, 等. JOB-9003高聚物粘结炸药热冲击损伤破坏相关性研究[J]. 含能材料, 2004, 12(3): 174-177.

TIAN Yong, ZHANG Wei-bin, WEN Mao-ping, et al. Research on correlation of thermal shock damage of PBX JOB-9003[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2004, 12(3): 174-177.

[3] Willey T M, Van Buuren T, Lee J R, et al.Changes in pore size distribution upon thermal cycling of TATB-based explosives measured by ultra-small angle X-ray scattering[J].Propellants,Explosives,Pyrotechnics, 2008, 31(6): 451-466.

[4] Cornell R H, Johnson G L. Measuring thermal diffusivities of high explosives by the flash method[J]. Report No.UCRL-52565, October 1978.

[5] Kroonblawd M P, Sewell T D.Thomas D.Sewell. Theoretical determination of anisotropic thermal conductivity for crystalline 1,3,5-triamina-2,4,6-trinitrobenzene(TATB)[J].TheJournalofChemicalPhysics, 2013, 139(7): (074503-1)-(074503-10).

[6] 周筱雨, 王翕, 韦兴文, 等. 基于分形方法的高聚物粘接炸药导热系数预测模型[J]. 含能材料, 2014, 22(4): 535-541.

ZHOU Xiao-yu, WANG Xi, WEI Xing-wen, et al. Prediction model for thermal conductivity of PBX based on fractal approach[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2014, 22(4): 535-541.

[7] Hasselman D H P. Effective thermal conductivity of composites with interfacial thermal barrier resistance[J].JCompMater, 1987, (21): 508-515.

[8] Benvensite Y. Thermal conductivity of composites materials[J].JApplPhys, 1987 (61): 2840.

[9] Every A G. The effect of particle size on the thermal conductivity of ZnS/diamond composites[J].ActaMetallMater, 1992, 40(1):123-129.

[10] Wang Jiajun, Yi Xiaosu. Effects of interfacial thermal barrier resistance and particle shapeand size on the thermal conductivity of AlN/PI composites[J].CompositesScienceandTechnology, 2004, 64(10-11):1623-1628.

[11] Bruggeman D A G. Dielectric comstant and conductivity of mixtures of isotropic materials[J].AnnPhys, 1935, 24: 636-679.

[12] 任晓婷, 杨利, 张国英, 等. TATB晶体形貌的计算模拟[J]. 火炸药学报, 2010, 33(6): 43-46.

REN Xiao-ting, YANG Li, ZHANG Guo-ying, et al. Computational simulation of the crystal morphology of TATB[J].ChineseJournalofExplosivesandPropellants, 2010, 33(6): 43-46.