把握数学本质发展思维能力——《解决问题的策略（画图）》教学设计与思考（二）

董 良

【教学内容】

苏教版四年级下册第48～49页例1、练一练和练习八第1～4题。

【教学过程】

一、沟通旧知，引入策略

1.出示线段图：

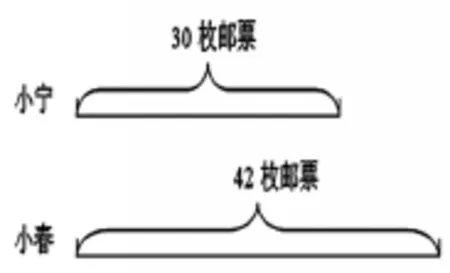
图1

提问：（1）从这幅图上，你能获得哪些数学信息？

（2）从这幅图中我们可以求出什么？能在图上表示出来吗？

预设：小春比小宁多多少枚邮票？小宁和小春一共有多少枚邮票？

根据学生的回答引导学生在线段图上表示出所求问题，并在实物展台上演示。

2.谈话引入：我们在二年级已经学过用画图来解决实际问题，你们觉得画图的方法怎么样？（直观、清楚）

今天，我们将进一步学习这一解决问题的策略。

（板书：解决问题的策略）

【设计意图：学生在二年级已经初步接触了画线段图，让学生根据已有的线段图提出问题，可以培养学生发现问题、提出问题的能力，同时也激活学生已有的学习认知，唤醒学生原有的画图经验。通过这样的导入，学生能够顺其自然地进入到新课的学习过程中，不知不觉中开启策略的探索之旅。】

二、自主合作，探索策略

1.出示例1：小宁和小春共有72枚邮票，小春比小宁多12枚。两人各有多少枚邮票？

（1）引导读题，说说题目中地哪些数学信息？求什么问题？

（2）提问：怎么才能更清楚的表示两者的关系呢？（画图）

2.引导画图，理清数量关系。

（1）示范画图，提醒：题目中有两个相关联的量，应该用两条线段来表示。小宁的邮票枚数少，画的短一些；小春的邮票枚数多，画的长一些。

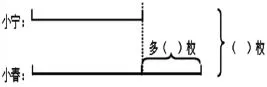
图2

（2）提问：你能根据题意把线段图填写完整吗？

学生在数学书上把线段图补充完整。

（3）看图说题意（隐去题目）。

提问：看着线段图，你能说一说这道题目的条件和问题吗？

（4）比较：同一道题目，对于文字和线段图，你更喜欢哪一种呈现方式？为什么？

3.尝试解答，初步建构策略。

（1）提问：观察线段图，想一想可以先算什么？你能自己尝试解答吗？

学生通过观察线段图，自主尝试解答，把解题过程写在练习纸上。

谈话：已经写完的同学，请在小组里，结合你的线段图，说一说，你是怎么想的？

教师可以边巡视，边挑选正确的、不同的写法，请学生到黑板前板书。

（2）反馈交流。

请学生交流解题思路。

汇报预测：

解题思路一：先算出小宁有多少枚邮票。两人邮票的总数减去12枚，等于小宁邮票枚数的2倍。

小宁：（72-12）÷2=30（枚）

小春：72-30=42（枚）

解题思路二：先算出小春有多少枚邮票。两人的总数加12枚，等于小春邮票枚数的2倍。

小春：（72+12）÷2=42（枚）

小宁：72-42=30（枚）

解题思路三：先算出小春给小宁6枚邮票后两人邮票枚数就一样多，平均每人有36枚邮票。

72÷2=36（枚）

12÷2=6（枚）

小春：36+6=42（枚）

小宁：36-6=30（枚）

（这种算法视课堂反馈情况而定，学生没有出现这种算法就不交流）

在学生交流的过程中，教师适时引导：你能在线段图上表示出这一步的含义吗？

学生讲解完，教师可以继续提问：你们觉得他讲的怎么样？还有什么补充吗？

（3）组织检验。

提问：我们用什么方法进行检验？

追问：检验要分几步进行？

学生独立进行检验，并写出答案。

【设计意图：问题解决能力对于培养数学学科的核心素养极其重要。通过“画线段图”，渗透数形结合的思想，学生发现运用线段图，数量之间的关系比文字叙述更清晰，从而能更加直观地分析问题，提出假设。教师适时引导后选择大胆放手，让学生先独立思考，再讨论交流，既可以假设让小宁的邮票增加12枚，这样邮票总数就是小春的2倍；也可以假设让小春的邮票减少12枚，这样邮票总数就是小宁的2倍，得出答案后教师不忘引导学生验证，从而完整地呈现了问题解决的四个阶段，即：发现问题、分析问题、提出假设、检验假设。】

三、回顾反思，梳理策略

1.提问：黑板上的这三种算法虽然解题思路不一样，但是他们有没有相同点呢？

相同点：都用了画图的策略；都设法使两人邮票的数量变得同样多。（板书课题：画图）

总结解题步骤（画图、分析解答、检验），并让学生说说对画图策略的体会。

2.交流讨论，提升策略意识。

谈话：的确，当我们遇到比较复杂的问题时，可以尝试用画图表示题意，画图可以让数量关系更直观、更清楚，可以帮助我们很快找到解决问题的方法。（板书：直观、清楚、方便分析）

提问：我们曾经运用画图的策略解决过哪些问题？

根据学生回答，课件出示：

图3

小结：画图是解决问题常用的策略，所以，我们一定要学好画图的策略。

【设计意图：通过对三种解题思路的对比，找出解题策略的不同点，也找到策略的相同点：都设法使两人邮票的数量变得同样多。同时也梳理了以往的学习过程中运用画图的策略解决过哪些问题，学生发现画图策略贯穿在我们的学习过程中，更加能体会到画图策略的优势，对策略的理解更加立体和完整。】

四、巩固练习，运用策略

完成教材第49页“练一练”和教材第52页“练习八”第1、2、3 题。

【设计意图：课堂练习是数学课堂教学的一个重要组成部分，学生将所学的知识在实践中加以应用，检验自己对所学知识的理解程度，给教师反馈信息，以便教师进行纠错和指导。练习的设计，从说线段图到画线段图，从两个量到多个量，由易到难，层层递进，通过适度挖掘和拓展，用多样化的形式帮助学生深入理解，加深了学生对策略的理解，更好地掌握用画线段图来解决问题。】

五、交流收获，提升策略

谈话：同学们说说你在这节课上收获了什么？画线段图解决问题有哪几个步骤？

小结：今天学习了画线段图解决问题的策略。画图，能够让我们更加清晰、直观、简单地描述题中的数量关系。

展望：数学大师华罗庚说过：“数形结合百般好，数形分离万事难。”希望同学们在今后的学习过程中能够主动用画图的策略解决生活中的实际问题，养成画图解决问题的习惯。

【设计意图：最后的课堂小结，进一步强化了画图策略的步骤，加深了对策略的理解。以华罗庚的名言收尾，将策略意识从课堂延伸到课外，更好地运用到实际生活中去。】