数学与美术的整合——《学剪双喜——轴对称图形拓展课》设计与解读

吴燕燕

一、教学内容的确定

1.产生的背景。

学生学完《轴对称图形》一课后，班级里出现了一场剪纸热，很多学生能剪出简单的轴对称图形，有的学生还能利用轴对称图形的知识剪出漂亮的窗花。

2.内容的确立。

双喜既是典型的轴对称图形，又是我们中国剪纸的文化艺术。同学们熟悉它，喜欢它，学会剪双喜既是一门技术，又是培养学生观察能力、动手能力和空间想象能力的好材料。通过学习剪双喜既能让学生感受到数学与生活的密切联系，又能使学生体验到成功的快乐，觉得数学好玩，同时也让学生了解中国剪纸的艺术魅力。通过这节课的学习，为之后学习例4剪四个手拉手小人打下扎实的基础，也很好地培养了学生的空间观念。

二、教学内容的分析

1.相关内容分布。

（1）在人教版二年级“图形与变化”中安排了“你知道吗？”对于学生来说，虽说幼儿园有过剪纸经验，但剪窗花的生活经验不丰富，学生很难与“轴对称”的数学知识产生联系。

（2）剪“拉手小人”。

本单元教材编排了“非常规问题解决”内容，剪出“拉小手的四个小人”，学生通过动手剪一剪，结合剪出的图形加深对图形的平移和旋转的认识。

2.本节课的结构确定。

由于是拓展性课程的尝试，所以还没有形成教材的编排。但是我希望通过本课加强数学课程内部的拓展，对“你知道吗？”内容进行两个维度的延伸：对“数学知识的应用和深化”和对“传统文化的体验和认识”。

我认为，在“拉手小人”中“剪”是手段，“概念”的深化是目标，剪出的图案则是副产品。而在拓展课中，“剪出双喜”本身就是目标维度里的核心部分，只有学生体会剪双喜的成果才会进一步体会传统文化的认识。

三、教学目标

1.通过剪双喜的活动，学生经历观察、思考、想象、操作等活动的过程，学会剪标准的双喜。通过活动，还发现对折次数与平均分成份数的关系。

2.通过活动，培养学生动手操作能力、合作能力、空间想象能力。让学生意识到几何直观的好处，也初步体验到平面图形由局部到整体的变化过程。发展学生的数学思维。

3.使学生感受到数学与生活的密切关系和学习数学的成功体验。同时渗透中国剪纸艺术的魅力。

四、教学设计与解读

1.通过剪爱心引入新课。

师：同学们，你会剪爱心吗？看谁剪得又美观又快。

反馈：比较两种剪法。

（1）直接剪；

（2）对折一次剪。

师：你们喜欢哪种剪法？

师：对折后剪有什么好处？这是利用我们学过的什么知识来剪的？中间这条折痕叫什么？爱心就是一个轴对称图形。

（课件演示剪爱心过程，并出示对称轴，轴对称图形）

小结：看来利用对称知识能使我们剪的图形既美观又快。今天我们就利用对称知识来剪双喜。

板书课题：学剪双喜

【解读：这个环节通过让学生动手剪爱心，在比较中得出对折剪的好处，同时复习了轴对称图形的相关知识，为下文探究剪双喜方法打下基础。】

2.探究剪双喜的方法。

教师在黑板上出示一个双喜。它是轴对称图形吗？怎么找它的对称轴？

（课件演示对折过程再展开，出示对称轴和轴对称图形）

师：如果剪这样一个双喜，你觉得需要做几步？

（同桌讨论、反馈）

生：对折，画，剪。

师：你的意思是对折一次后再画？画什么？

生：（预设：对折两次再画，画半个喜，最后剪）

师：到底是对折一次，还是对折两次，哪种好？

师：请同学们拿出双喜先仔细观察，再来折一折研究研究。并思考两个问题：

（1）对折一次，还是两次？

（2）如果两次，怎么对折？

反馈：

生：对折一次。

生：对折两次。

师：你是怎么对折的？谁看懂了?谁也是这么这么对折的？（贴在黑板上）

课件演示两种对折过程。

课件出示两种图：

比较：对折一次后与对折二次后有什么不同？

思考：哪种好？为什么对折两次比对折一次好？（课件回放还原过程）

结论：对折一次后是一个“喜”字，一个“喜”还是一个轴对称图形，剪的时候中间需要挖两个口，不好剪。对折两次后是半个“喜”字，这时不是轴对称图形，可以直接剪。所以对折两次比对折一次好剪，且方便。

每个同学选一张纸对折两次并展开，发现把正方形纸平均分成了几份？再还原。还发现对折两次后出现一边是分开的，我们为了表达方便，分开的这边叫开口处，另一边叫封口处）

【解读：此环节让学生通过观察双喜，并动手操作，同桌讨论等活动，得出对折两次比对折一次好剪的原因。也让学生意识到几何直观图带来的好处。】

师：折解决好了，怎么画呢？画什么？画在哪边？继续仔细观察半个喜，它有什么特点？

（提示：半个喜共有几个缺口，右边几个？左边几个？把缺口部分画出来并打个×）

师：怎么剪？从哪里剪？一共剪了几个地方？（继续观察半个喜）（课件演示）

师：根据刚才探究的步骤来剪一剪双喜。

（学生活动剪双喜）

反馈：展示学生作品

谈谈正确剪法的成功经验，分析错误剪法的原因。

分析错误的原因：说说错在哪里？哪个步骤出现错误？

视频播放剪双喜的过程。

小结：同学们回想一下，刚才我们是怎么学会剪双喜的？我们先通过观察发现双喜是轴对称图形（板书观察），还发现对折两次的好处，又通过观察我们学会画半个喜，还学会了怎么剪。在数学学习中观察是一种很重要的学习方法，除了观察，我们还必须要认真思考（板书：思考），再动手操作（板书：操作），最后才成功剪得双喜。（观察→思考→操作）

【解读：这个探究环节主要让学生通过几个不同层次来探究剪红双喜的方法。第一，学生先观察、折现成的双喜，同桌讨论，发现对折两次后，再画，最后剪分三步即可剪得双喜。第二，学生根据探究的步骤动手剪双喜。第三，全班交流剪双喜的成功经验及分析剪失败的原因。第四，播放视频剪双喜的过程。让更多的学生学会剪双喜，让尽可能多的学生分享成功的快乐。最后让学生总结剪双喜的方法，为剪其他图形埋下伏笔。这个过程是比较开放的，学生自主探究，不断尝试，交流经验，总结方法。这个环节更让学生意识到图形的直观带来的好处（几何直观），也让学生体验到图形从整体到局部，从局部到整体还原的变化过程。（培养学生的空间观念）】

3.拓展练习。

（1）欣赏生活中变形的双喜（课件出示）。

①对比观察：仔细观察这四个双喜，与标准的双喜相比哪里发生了变化？在剪的过程中需要注意哪些地方发生变化？②先独立思考，再小组交流。

每个小组分工合作，说说每个变形的双喜哪里发生了变化？

学生活动，再展示。

（2）找朋友：看图形的一部分，想象展开后的图形，并用线连接起来。

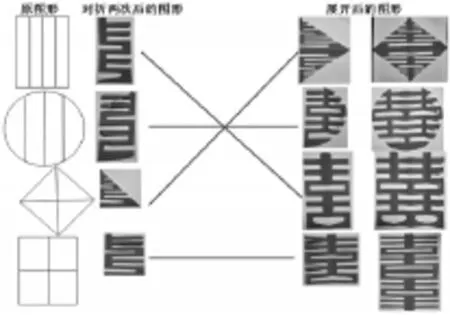
（3）探究双喜中藏着的规律。

①刚才我们都对折了两次，剪出了双喜，如果对折三次，能剪出几个双喜？把长方形纸或正方形纸平均分成了几份？（学生操作对折三次）②如果对折四次呢？你有什么发现？

完成表格：

把长方形或正方形平均分成 喜的个数对折1次 （2）份 （1）个对折2次 （4）份 （2）个对折3次 （ ）份 （ ）个对折4次 （ ）份 （ ）个你有什么发现：

【解读：练习环节很好地培养了学生观察能力和空间想象能力。同时发现对折次数与平均分成的份数的关系及喜的个数的关系。拓展发散了学生的思维。】

4.课堂总结。

通过这节课的学习，你最大的收获是什么？你还有什么想说的吗？

总结：剪双喜只是剪纸艺术中一小部分。中国的剪纸艺术历史悠久，希望同学们用数学的眼光去观察、去思考想象、去操作，学会更多的剪纸艺术。

5.作业设计。

（1）剪四喜临门的双喜。

（2）剪出几个变形的双喜。

（本文作者系朱乐平数学名师工作站“一课研究”组成员）