探研六阶微分系统主次特征值之比的下界
黄振明
(苏州市职业大学 数理部,江苏 苏州 215104)
探研六阶微分系统主次特征值之比的下界
黄振明
(苏州市职业大学 数理部,江苏 苏州 215104)
对六阶微分系统广义低阶特征值进行定量分析,运用经典的Sturm-Liouville特征值定性理论,利用矩阵运算、分部积分、测试函数和Schwartz不等式等具体方法,找到了所论问题的主特征值与主特征向量间的关系,并获得了主次特征值之比的下界估计不等式,此界仅与系统的系数有关,而与所论区间的几何度量无关,其结果是参考文献结论的进一步推广。
六阶微分系统;特征值;Rayleigh定理;特征向量;估计下界
在用分离变量法讨论偏微分方程的定解问题时,首先需将问题转化成常微分方程的特征值问题,然后根据边界条件,得到特征值所满足的方程。绝大多数情形下,这类方程为超越方程,因而没有求特征值和特征函数的一般方法,从而无法求得特征值的精确值,但在物理学、弹性力学和生物学等许多学科中常需对某个微分方程或方程组的前几个特征值作定量分析,因为实际系统的重要物理特性主要由这几个低阶特征值来反映,既然无法求得问题的精确值,退而次之,估计其范围不失为一种选择。因此,本文考虑如下由任意多个方程构成的一类六阶微分系统广义特征值的估计问题
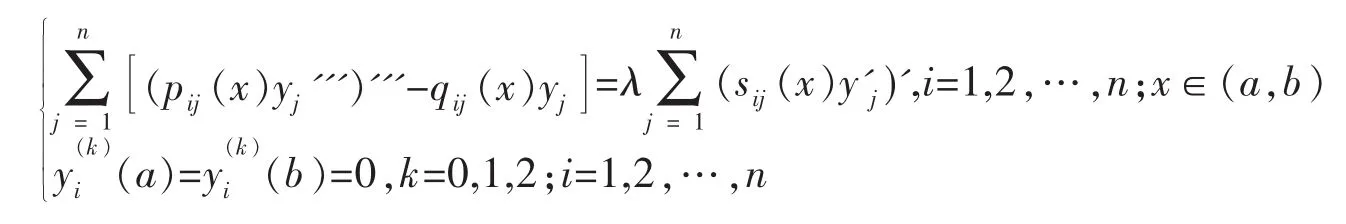
其中(a,b)⊂R是一个有界开区间,pij(x)∈C3[a,b],qij(x)∈C[a,b],sij(x)∈C1[a,b],且满足pij(x)=pji(x),qij(x)=qji(x),sij(x)=sji(x)(i,j=1,2,…,n),为简化推导过程,引入下面矩阵和向量的记号:
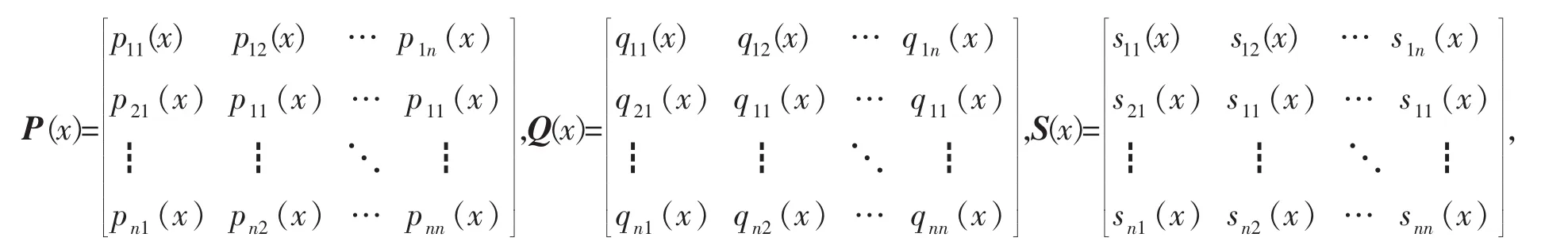
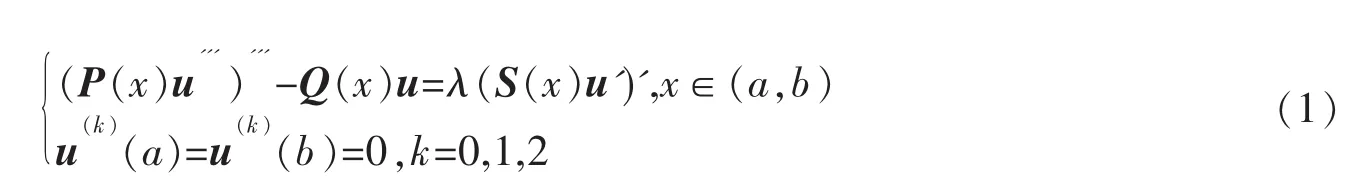
且满足如下正定或半正定条件:对任意n维向量ξ=(ξ1,.ξ2,…,ξn)T,有

上述μi,υi(i=1,2)均为正常数,T为转置符号。
特征值估计问题是特征值理论研究中的重要一环,近年来,随着估计理论的深入及估计方法的多样化,在此领域内又取得了一系列丰硕的研究成果[1-7],笔者参考文献[1]中对六阶微分方程特征值的讨论方法,获得了问题(1)主次特征值之比下界的如下估计结论。
定理1设λ1,λ2分别是问题(1)的主、次特征值(0<λ1≤λ2),则有

文献[1]讨论的六阶微分方程即是本文问题(1)当n=1,q11(x)=0,s11(x)=0时的特例,文献[2]讨论的六阶微分方程广义特征值问题也是问题(1)当n=1时的特例,文献[3]讨论的某类六阶微分系统是问题(1)当Q(x)=0(零矩阵)时的通常意义下的特征值含权估计问题,因此,问题(1)的广义特征值估计结果可视作是文献[1-3]的进一步推广,在数学、物理学和力学等学科中有着一定的参考和应用价值[8-10]。
1 定理的证明
首先说明问题(1)的特征值 λ都为正实数,在(1)两端同乘 u,再在区间(a,b)上积分,利用式(2)、(4)和分部积分公式,并利用到边界条件,可得

另外,由问题(1)中边界条件和式(3),可得

由上式和(5)知λ为非负实数。
另一方面,λ不会等于零,否则由式(5)知um=0,可推得u=c0+c1x+c2x2(其中c0,c1,c2为n维常向量),代入边界条件u(a)=u'(a)=u''(a)=0,即得c0=c1=c2=0,也即u=0,而这与特征向量为非零向量矛盾,所以λ>0。
设问题(1)的主特征值λ1对应的主特征向量为u,且满足

运用分部积分,有

由式(6)和(3),得

由问题(1),利用分部积分、式(6)和(4)有

利用式(2)和(8),得

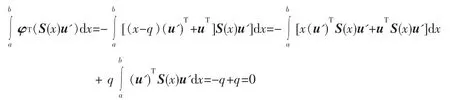
由此可知,φ与u广义正交,同时满足奇次边界条件:φ(k)(a)=φ(k)(b)=0,k=0,1,2),根据广义Rayleigh定理知,成立着
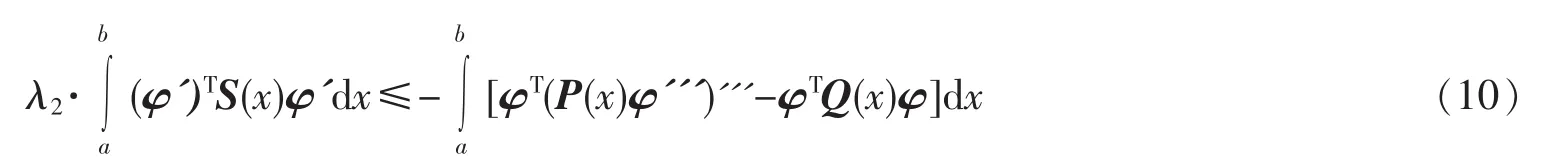
利用φ的定义和式(1),计算可得

因此
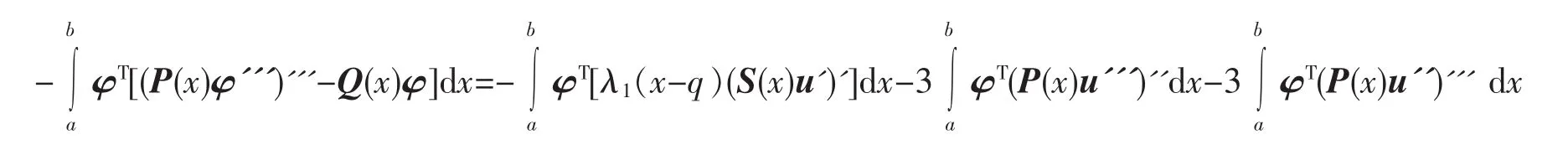
另一方面
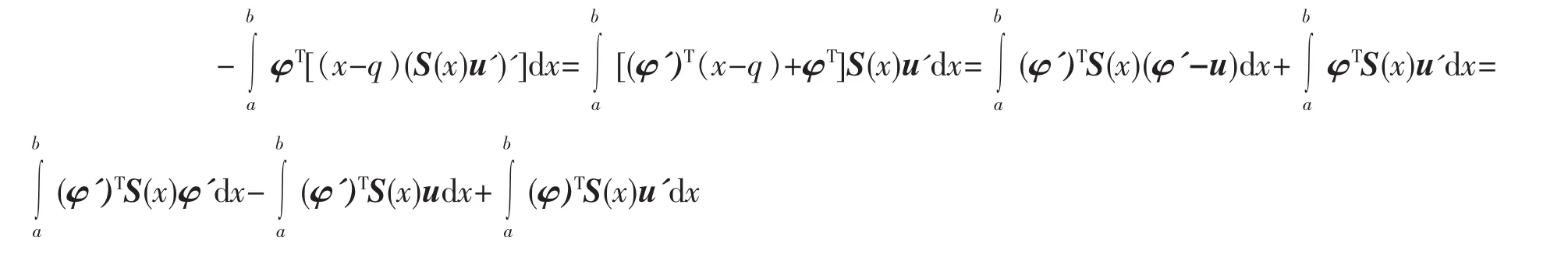
根据上面两式可得
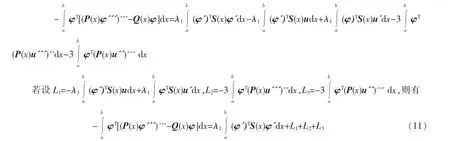
利用式(10)、(11),有

引理1设u是问题(1)对应于主特征值的主特征向量,则与满足如下一系列不等式

证明:利用P(x)的正定性、式(2)、(7)和(8),有
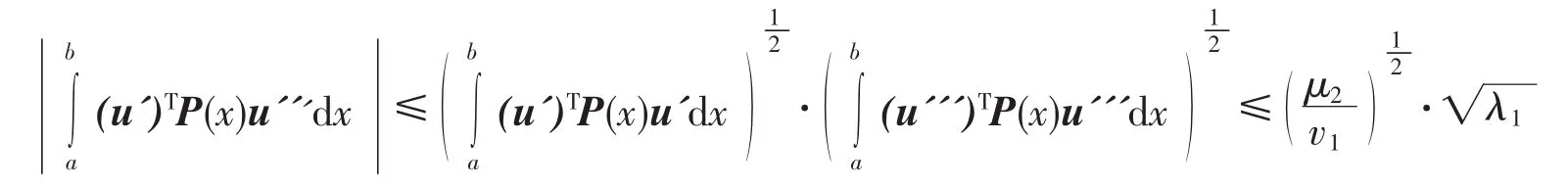
即得引理1(a)。
利用分部积分和Schwartz不等式、式(7)和(9)得

即得引理1(b)。
由式(7)、分部积分、Schwartz不等式、(3)和引理1(b)得

化简即得引理1(d)。
引理2 设λ1是问题(1)的主特征值,则

证明:利用分部积分和φ的定义,计算可得

类似可得

于是
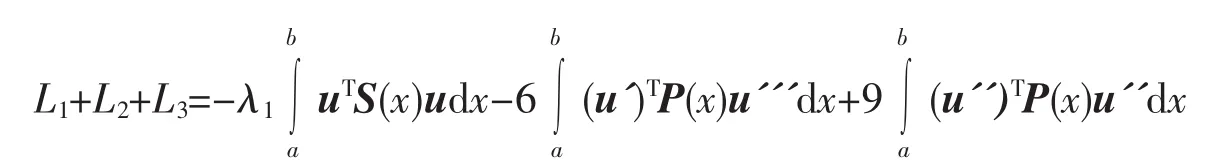
将引理1的估计结论代入上式右端,有
引理2证毕。
引理3对于上述定义的试验函数φ与主特征值λ1,下列不等式恒成立

证明:利用分部积分和φ的定义,并结合边界条件有

由此可得

利用式(13)、(7)、Schwartz不等式、(3)和引理1(b)得

整理上式,即得引理3。
定理1的证明:将引理2的估计结论代入式(12)右端得

再将引理3的估计不等式代入上式左端,经化简整理即得定理1的结论。
2 一般情形
现再将定理1的结论进一步推广至如下一般情形的偶数阶微分系统:


定理2 设λ1,λ2分别是问题(14)的主、次特征值(0<λ1≤λ2),则有
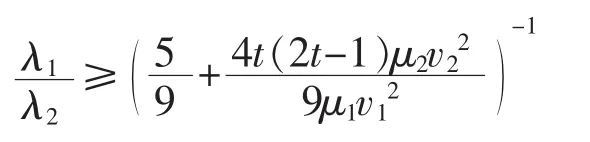
易见当t=3时,定理2即为定理1。
3 结语

[1]韩秋敏,钱椿林.六阶某类微分方程第二特征值的上界[J].苏州大学学报,1999,15(4):26-30.
[2]黄振明.六阶微分方程第二广义谱的含权上界估计[J].嘉应学院学报,2012,30(11):10-13.
[3]黄振明.一类六阶微分系统特征值的上界估计[J].甘肃联合大学学报:自然科学版,2007,21(1):11-15.
[4]金光宇,钱椿林.四阶常微分方程的特征值估计[J].苏州丝绸工学院学报,1996,16(4):115-119.
[5]吴平,钱椿林.梁横向振动方程的离散特征值估计[J].江苏广播电视大学学报,2001,12(6):40-42.
[6]张长青,钱椿林.某类微分系统第二特征值的上界估计[J].江苏广播电视大学学报,2002,13(6):34-36.
[7]胡志坚,钱椿林.四阶微分方程广义第二特征值的上界估计[J].江南大学学报(自然科学版),2005,4(4):427-430.
[8]PROTTER M H.Can one hear the shape of a drum?[J].SIAM Rev,1987,29(2):185-197.
[9]HOOK S M.Domain independent upper bounds for eigenvalues of elliptic operator[J].Trans Amer Math Soc,1990,318:615-642.
[10]ASHBAUGH M S.The universal eigenvalue bounds of Payne-Polya-Weinberger,Hile-Protter,and H C Yang[J].Proc Indian Acad Sci Math Sci,2002,112(1):3-30.
(责任编辑:朱联九)
On the Lower Bound of the Ratio of Principal Eigenvalue to Secondary One for Differential System with Sixth-order
HUANG Zhen-ming
(Department of Mathematics and Physics,Suzhou Vocational University,Suzhou 215104,China)
The quantitative analysis of generalized lower-order eigenvalues for differential system with sixth-order is conducted in this paper.The relationship between principal eigenvalue and its eigenvector is found by using classical Sturm-Liouville's eigenvalue qualitative theory,matrix operation,integration by parts,trial function and Schwartz inequality etc.The inequality of the lower bound of the ratio of principal eigenvalue to secondary one is also gained.This bound is only dependent of the system's coefficients,but not the measure of the domain in which the problem is concerned.The results are the further extension of the conclusion of the bibliography.
sixth-order differential system;eigenvalue;Rayleigh theorem;eigenvector;lower bound estimate
O175.9
A
1673-4343(2017)02-0011-06
10.14098/j.cn35-1288/z.2017.02.003
2016-11-20
黄振明,男,江苏苏州人,副教授。主要研究方向:微分算子的特征值估计。

