近岛礁地形影响下的浮式平台运动响应
杨 鹏,顾学康
(1.武汉第二船舶设计研究所,武汉430205;2.中国船舶科学研究中心,江苏 无锡214082)
近岛礁地形影响下的浮式平台运动响应
杨 鹏1,2,顾学康2
(1.武汉第二船舶设计研究所,武汉430205;2.中国船舶科学研究中心,江苏 无锡214082)
近岛礁附近的地形一般呈现高低不平的状态,水深从几十米到几米不等。远场波浪向近岸传递过来时在礁盘上会经过复杂的演化,使得浮体附近的波浪呈现一定的非均匀性,不同于常规的长峰规则波,同时礁盘的起伏变化会对波浪中的浮体的运动产生影响,最终使得浮体在复杂地形下的水动力运动响应不同于一般均一水深下的浮体响应。该文通过建立浮体和礁盘地形的耦合水动力模型,计算了礁盘对浮体入射波力、绕射力、辐射水动力系数以及运动的影响,同时与水池模型试验对比了浮体运动,两者较为一致。研究表明复杂地形对浮体的水动力运动存在较大的影响,在某些周期附近会增大浮体的运动响应,因此需要理性考虑复杂地形对浮体的影响。
近岛礁;地形;浮式平台;水动力耦合;波浪演化
0 引 言
大陆及岛屿的近岸附近一般水深较浅,呈现高低起伏状态。近年来在近岸附近部署浮式结构物的应用原来越多,例如LNG加气站[1]。另外随着开发和建设岛礁的需要,越来越多的国家开始研究近岛礁附近浮式结构物的应用,如图1-2所示。这些方面的研究均会涉及到不均匀海底影响下浮式结构物的水动力运动和载荷响应,但是该研究与浮式结构物在常规情况下(深水或均一有限水深)不同。
首先涉及到波浪从远场向近岸传播时,水深不断减小,在这些高低不平海底的影响下,波浪会出现散射、绕射、反射、折射、破波、底部摩擦和渗透等非线性演化现象,如图3所示。波浪环境中浮体与波浪存在着复杂的相互作用关系,因为浮体的存在,波浪在经过浮体时有绕射效应,这种绕射力和入射波浪力共同构成了外界波浪激励力,同时浮体在波浪的作用下会产生运动,如图4所示,兴起波浪向外辐射,这种效应在浮体上体现为水动力附加质量和阻尼。在处理岛礁附近局部流场的波浪演化时,现在比较常用的方法是Boussineq方程[2-3],基于该方法发展的比较成熟的软件如Funwave[4-5]。另外求解浮体在波浪中的运动一般采用基于势流理论的格林函数方法,但是该方法无法精确考虑波浪的非线性演化规律。因此Bingham (2000)[6]结合Beoussineq方程和格林函数方法探索性研究了L型平底港池里面浮体在波浪环境中的运动规律。Buchner(2006)[1]以一艘大型LNG船为对象,研究了其在平整斜坡上的水动力运动响应,文中基于面元法采用了浮体和地形耦合模型,并与试验结果进行了比较研究。Ferreira和Newman[7]变换地形宽度、长度、斜坡过渡段等,研究了该LNG船和地形的耦合影响,研究结果表明地形的尺度和形状对浮体的运动影响较大,不合理的模型将会使得过高估计地形对浮体运动的影响。田超等[8]使用简化的方法计算了近岛礁附近浮式结构物的运动响应,其中波浪从远方过来的演化过程使用缓坡方程计算波浪衰减系数,浮体运动单独使用均一水深边界元法计算,通过将该运动结果乘上衰减系数来考虑地形对浮体运动的影响。

图1 岛礁附近的海底剖面图Fig.1 Section of seabed near island

图2 岛礁附近的浮体Fig.2 Floating structure near island

图3 近岸附近波浪演化[8] Fig.3 Wave evolution near shore

图4 浮体在波浪中的运动Fig.4 Motion of floating structure in waves
可见在岛礁附近浮体在波浪中的运动规律既不同于无限水深和均一有限水深情况,同时又需要考虑波浪演化,是一个十分复杂的问题。本文将基于格林函数的边界元方法针对某一岛礁附近的实际海底三维地形开展浮体与地形的耦合响应分析,同时通过一定的相似比关系开展了水池模型试验,通过试验研究了浮体在复杂地形上的水动力运动规律以及波浪演化规律。本文将结合试验结果,比较研究数值计算结果与试验的差别,同时进一步深入研究影响浮体运动的主要因素和数值分析手段的合理性。
1 模型试验
1.1 模型设计
本文以一艘半潜浮式平台为研究对象,其主要参数如表1所示。模型试验采用1:36缩尺比,模型长1.389 m,试验地形图和试验模型如5~7所示,试验中平台采用桩柱式系泊。海洋结构物在波浪中运动的相似律问题,通常忽略粘性的影响,模型和实体的两个系统应该满足三个相似条件,即:几何相似、运动相似和动力相似,即,

式中:L、V、T分别为特征线尺度、特征速度和周期,下标m和s分别表示模型和实体。
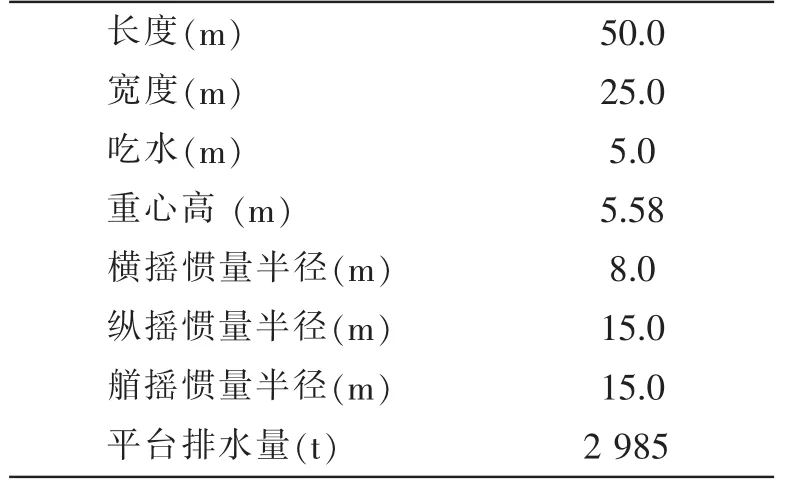
表1 浮体主要参数Tab.1 M ain parameters of floating structure

图5 试验地形Fig.5 Seabed inmodel test

图6 浮体水动力模型Fig.6 Hydrodynamicmodel of floating structure
1.2 静水衰减试验
试验中确保模型的运动固有周期与实际浮体的一致性十分重要,通过在静水中开展模型的运动衰减试验可以获得模型的运动固有周期和衰减系数,下表2和表3分别给出了试验中运动固有周期和衰减系数。从表2中可以发现模型试验与数值计算结果差别较小。

表2 运动固有周期Tab.2 Natural periods ofmotion

图7 波浪中的模型试验Fig.7 Model test in waves

表3 衰减系数Tab.3 Damping ratio
1.3 试验结果
以远方规则波来浪的周期为横坐标,图9中给出了90°横浪情况下试验传递函数与数值计算结果的比较。其中浮体水动力数值计算的地形模型视图如图8所示,地形面长250 m,宽200m(地形的长度方向沿着浮式平台的宽度方向,而宽度沿着平台的长度方向),地形完全浸没于水面以下,海底边缘深度为35.6m,边缘采用平滑过渡,地形深度从35.6m逐渐变化到岸上为0m,在平台布置点处水深为10m。其中浮体网格为1 992个,地形网格为11 908个,整个模型湿网格为13 900个,图8为岛礁建设浮式平台带地形三维视图和水动力模型。使用三维水弹性软件THAFTS求解该模型时需要在64位服务器上进行。一般情况下波浪从外面海域向岛礁岸边传播,因此本文重点考察90°浪向下的浮体水动力响应。
从图9中可以看出在小周期段(约小于13 s)试验结果、耦合模型和10m均一水深模型三者之间的计算结果较为一致,超过15 s之后,耦合模型计算结果与试验更为接近。这与物理现象也是吻合的,大周期波浪在地形上的演化效应比较明显。另外在图9(a)中显示13s周期附近浮体横荡运动有波动,耦合模型也有类似现象,而均一水深计算结果为一条直线。因此在复杂三维浅水地形中,需要利用耦合模型计算浮体在波浪中的运动响应,尤其在大周期情况下耦合模型的计算结果大于均一水深下的计算结果。另外在图9(c)中的5 s周期附近试验值小于数值计算结果,这可能与试验中采用了桩柱式系泊有关,因为该种系泊形式较强地约束了横摇,而数值计算中没有考虑系泊系统的影响。

图8 浮体与地形耦合模型Fig.8 Couplingmodel of floating structure and seabed

图9 浮体运动传递函数Fig.9 Transfer function ofmotion of floating structure
2 数值分析
本文计算浮体与地形耦合响应时采用的是三维频域线性边界元计算程序,其成立的前提是对于规则入射波浮体周围的波浪数据(例如波高、压力、速度场等)还是正弦变化,是不能够考虑波浪在浅水中演化时的破碎等现象。在数值分析时分别计算了以下三种模型中浮体的水动力系数、波浪激励力和运动:(a)浮体和地形耦合模型,计算水深设置为地形边缘的深度35.6m;(b)单独浮体,均一水深10m(平台布放处水深);(c)单独浮体,均一水深35.6m。

图10 附加质量Fig.10 Added mass
上面通过试验数据与数值计算结果的比较,在一定程度上验证了计算模型和方法的合理性,但是仅仅只是比较了浮体运动,而浮体的运动由流体作用在其上的水动力附加质量、阻尼和波浪激励力决定,因此有必要从更深层次分析影响浮体运动的主要因素。图(10)中给出了耦合模型、10m均一水深模型、35.6 m均一水深模型下无量纲的附加质量计算结果,计算结果显示三种计算模型的Surge和Yaw模态下的附加质量计算结果十分接近,而其他四个运动模态存在较大差别。另外图10(b)中显示耦合模型与10m均一水深模型的附加质量在很多频率处较为一致,可见地形对浮体运动水动力系数的影响是非常强烈的,即使计算水深取为地形边缘处,经过地形影响后浮体的水动力系数可以接近于浮体在当地水深下的水动力系数。总之,地形对浮体水动力系数的影响非常大,不能简单地当作均一水深情况处理。
图11给出了耦合模型、10 m均一水深模型、35.6 m均一水深模型下作用在浮体上的波浪激励力,图中同样显示三者的计算结果存在较大差别。由于在试验中并没有单独测量波浪激励力,因此图中计算结果的合理性很难直接验证。

图11 波浪激励力传递函数Fig.11 Transfer function ofwave exciting force
在模型试验中单独测量了波浪经过地形演化后的波高测量结果,通过这些数据可以获得波高演化规律。如果在规则入射波情况下,经过演化后的波浪还是正弦变化的,那么至少让采用频域边界元方法计算浮体波浪激励力的前提成立了。图12给出了地形的剖面图,通过2#、6#、10#、14#和18#共五个浪高仪测量波浪在地形上的演化规律,其中18号浪高仪测量未经地形影响的入射波高,平台布置在6#右侧。

图12 地形剖面图Fig.12 Seabed section
图13给出了模型试验中2m规则波在地形上的变化规律,从图中可以看出18#、2#和6#处的波高依然服从正弦变化规律,10#处波高具有明显的非线性,波谷变平坦,波峰变尖,此时地形已经很浅,而且波浪周期越大非线性越明显。由于浮体布置在6#附近,因此其周围的波浪经过演化后仍可看成是正弦变化的,可见前面在使用频域边界元方法计算耦合模型的水动力响应时的假设得到了满足,而且之前的浮体水动力运动计算结果与试验吻合较好,因此本文利用该方法计算地形对浮体水动力运动的影响是合理的。如果浮体是布置在10#位置处,那么本文的计算方法需要改进后结合波浪演化程序在时域上计算浮体上的波浪激励力,例如结合Boussineq方程。

图13 波高演化规律Fig.13 Evolution principle ofwave height
3 结 论
通过建立复杂三维地形和浮体水动力模型,采用三维线性频域边界元方法开展了浮体与地形的耦合水动力分析,研究了浮体的水动力系数、波浪激励力和运动。同时为了验证本方法和计算模型的正确性,基于一定的相似比规律开展了水池模型试验,测量了波浪在地形上的传播规律以及浮体在复杂三维地形上的运动规律,经过比较分析,数值计算结果与试验数据较为一致。另外文中进一步研究了均一水深、耦合模型下水动力附加质量、波浪激励力等的变化规律,计算结果表明耦合模型与均一水深下的计算结果差别较大。总之复杂地形对浮体的水动力运动存在较大的影响,在某些周期附近会增大浮体的运动响应,因此需要理性考虑复杂地形对浮体的影响。而且如果外场波浪经过演化后在浮体周围的波浪信息为非线性,那么便不能当做正弦变化处理,就需要结合波浪演化程序在时域上计算浮体上的波浪激励力,例如Boussineq方程。
[1]Buchner B.Themotions of ship on a sloped seabed[C].Proc.25th OMAE,2006(OMAE2006-92321).
[2]Shi F,Kirby JT,Harris JC,Geiman JD,Grilli S T.A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation[J].Ocean Modelling,2012,43-44:36-51.
[3]Shiach JB,Mingham C G.A temporally second-order accurate Godunov-type scheme for solving the extended Boussinesq equations[J].Coastal Engineering,2009,56:32-45.
[4]Shi F,Kirby JT,Tehranirad B,Harris JC.FUNWAVE-TVD,Version 1.0,users’manual and benchmark tests[R].Center for Applied Coastal Research Report,CACR 2011-04,University of Delaware,Newark,Delaware,2011.
[5]Shi F,Tehranirad B,Kirby JT,Harris JC,Grilli S.Fully nonlinear Boussinesq wavemodelwith TVD solver documentation and user’smanual[K].2013.
[6]Binggham H B.A Hybrid Boussineq panelmethod for predicting themotion of amoored ship[J].Coastal Engineering, 2000,40:21-38.
[7]Ferreira M D,Newman JN.Diffraction effects and ship motions on an artificial seabed[C].24th IWWWFB,2009.
[8]田 超,丁 军,杨 鹏.岛礁波浪环境下浮式结构物的动响应预报[J].船舶力学,2014,18(11):1284-1291. Tian C,Ding J,Yang P.Prediction of dynamic responses of floating structures under wave environment near islands and reefs[J].Journal of Ship Mechanics,2014,18(11):1284-1291.
M otion responses of floating structures near small islands
YANG Peng1,2,GU Xue-kang1
(1.Wuhan Second Ship Design and Research Institute,Wuhan 430205,China; 2.China Ship Scientific Research Center,Wuxi214082,China)
The seabed topography near small islands is usually in rugged state,and the water depth can be changed from tens ofmeters to a few meters in a short distance.Far field waves advancing towards the shore will experience a complex evolution on the shoal.In this environment,the hydrodynamic responses of a floating structure will be largely affected by the non-uniform wave pattern and changeable seabed,and might be quite different from the general responses of a platform in waveswith uniform water depth.In this paper,a coupling hydrodynamicmodel of floating structures and reef topography was established;the incidentwave force,diffraction force,radiation hydrodynamic coefficients,motions of a floating structure were calculated. Themodelwas validated by comparing the predicted resultswith those ofmodel tests.It is indicated that complex sea bed topography has a significant influence on the hydrodynamic responses of the floating structure.Moreover,themotions are increased obviously in certain wave periods,with reference to that in far field waves.
near island;sea bed;floating structure;hydrodynamic coupling;wave evolution
U661.71 U674.38+1
:Adoi:10.3969/j.issn.1007-7294.2017.02.004
2016-09-28
国家973计划项目基金(2013CB036100)
杨 鹏(1988-),男,工程师,E-mail:yangpeng@cssrc.com.cn;顾学康(1963-),男,研究员。
1007-7294(2017)02-0152-07

