高超声速飞行器自适应神经网络控制

赵贺伟，胡云安，梁 勇，杨秀霞

(海军航空工程学院 控制工程系，烟台 264001)

高超声速飞行器自适应神经网络控制

赵贺伟，胡云安，梁 勇，杨秀霞

(海军航空工程学院 控制工程系，烟台 264001)

针对一类高超声速飞行器，在充分考虑其非线性模型包含未建模动态、气动参数变化、弹性形变等产生的未知非线性不确定函数以及外界扰动的情况下，设计了一种基于自适应神经网络的非线性逆控制器。首先，将系统的动态特性分为标称部分和不确定部分，采用非线性逆的思想设计标称部分的控制器，利用神经网络逼近不确定部分，将神经网络的最优权值采用自适应律进行调节，提高神经网络的在线逼近能力。利用改进的变结构控制来消除神经网络逼近误差的影响，最终使跟踪误差收敛为零，并保证闭环系统的信号有界。通过仿真验证了设计方法的正确性。

高超声速飞行器；自适应；神经网络；变结构控制

0 引言

高超声速飞行器是一种高速机动武器，在搜索信息、快速打击、大跨度预警等方面具有广泛的应用价值，一直是各国关注和研究的热点领域。高超声速飞行器的飞行跨度大，环境变化剧烈，气动参数的变化和外界干扰都不可避免，这些因素导致高超声速飞行器具有高度非线性、强耦合和不确定性，精确的动力学模型难以获得，这给控制器的设计带来了极大的困难和挑战。

对于高超声速飞行器控制器的设计方法，目前已有大量学者进行了研究，如文献[1]采用了基于H∞的方法设计了控制器，文献[2]采用了结构动力学的方法，设计了一种线性变参数控制器，上述2种方法都是基于线性模型进行的控制器设计，而线性模型难以全面刻画高超声速飞行器的动态力学行为；文献[3]设计了一种自适应控制器，文献[4]利用了观测器技术，设计了基于观测器的反馈控制器，文献[5]采用了一种模型跟踪控制方法设计了控制器，这3种方法都没有充分考虑模型的不确定性问题；文献[6-8]利用鲁棒非线性方法设计了控制器，但这些文献的研究对象是高超声速飞行器的纵向运动模型，而对于飞行器的横侧向运动没有进行研究；文献[9-10]将自适应控制与神经网络进行结合，设计自适应神经网络控制器，但神经网络逼近误差的处理不是很理想，这会影响系统的跟踪效果；文献[11]针对X-38高超飞行器的姿态控制，利用模糊逻辑方法设计了控制器，实现了姿态控制；文献[12]针对一种高超飞行器系统中存在的不确定性和外界扰动设计了一种鲁棒控制器，很好地实现了飞行器的姿态控制；文献[13]采用反演设计的思想，设计了基于反演的高超声速飞行器自适应滑模控制器，解决了模型中存在的不确定性问题，但外界扰动带来的影响没有加以考虑；文献[14]针对一种乘波体外形的高超飞行器，将系统在平衡点附近进行泰勒线性化，针对线性化后的模型，采用自适应线性二次型方法，实现镇定控制，但该方法具有较大的局限性，线性化后的模型不能够精确描述高超声速飞行器的全面动态特性；文献[15]采用自适应滑模控制方法，实现了一种外形为轴对称体的高超声速飞行器镇定控制,该方法的缺陷是不能解决非匹配不确定性问题。

本文主要采用非线性逆的思想来设计主体控制器，以保证闭环系统的全局稳定。利用神经网络来逼近因参数变化或建模误差引起的模型不确定部分，利用自适应调节律来调节神经网络的最优权值，提高神经网络的在线逼近能力。神经网络的逼近误差则由变结构控制策略来消除，并对变结构控制律进行改进，以削弱变结构控制产生的颤振带来的影响。

1 高超声速飞行器非线性模型

本文采用NASA兰利实验室高超声速飞行器Winged-Cone的非线性六自由度数学模型[16]，飞行器的结构布局及尺寸如图1所示。

具体数学模型如下：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

其中

D=qSCD，L=qSCL，Y=qSCY

MlA=qbSCl，MmA=mmrc-xcgZ

MnA=nmrc+xcgY，nmrc=qbSCn

mmrc=qcSCm，Z=-Dsinα-Lcosα

CD=CD，α+CD，δeδe+CD，δaδa+CD，δrδr

CY=CY，ββ+Cy，δeδe+CY，δaδa+CY，δrδr

CL=CL，α+CL，δeδe+CL，δeδe

Cl=Cl，ββ+Cl，δeδe+Cl，δaδa+Cl，δrδr+

Cn=Cn，ββ+Cn，δeδe+Cn，δaδa+Cn，δrδr+

Cm=Cm，α+Cm，δeδe+Cm，δaδa+

式中v为飞行速度；γ为航迹倾斜角；χ为航迹方位角；α、β、μ分别为迎角、侧滑角和速度滚转角；p、q、r分别为滚转角速率、俯仰角速率和偏转角速率；D、Y、L分别为阻力、侧力和升力；T为推力；Tx、Ty、Tz分别为推力在体坐标系上的分量；H为飞行高度；Ip、Iq、Ir分别为转动惯量；xcg为质心到参考力矩中心的距离；MlA、MmA、mnA为空气动力矩在体坐标系中的分解；CD、CY、CL分别为阻力、侧力和升力系数；δe、δa、δr分别为左、右升降副翼和方向舵偏转角；其余符号说明请参考文献[16]。

根据上述数学模型进行整理，可得

(10)

(11)

y=x1

(12)

式中x1、x2为状态量，x1=[αβμ]T，x2=[pqr]T；u为控制输入，u=[δeδaδr]T；y=x1为系统输出；f1、g1、f2、g2为非线性未知函数，f1(x1)∈R3、g1(x1)∈R3×3、f2(x1，x2)∈R3、g2(x1)∈R3×3；相关状态量、符号说明以及函数表达式详见文献[17-18]。

将非线性模型改写为如下形式：

(13)

其中

x=[x1，x2]T∈R6

F(x1，x2，t)=[f1f2]T∈R6

U=[1uT]T∈R4

式中x、f(x1，x2，t)、g(x1，t)、U为系统非线性未知函数[19]；d(t)为未知的外界干扰，d(t) ∈R6。

控制器设计的目的是使系统的状态x(t)能够跟踪期望的状态轨迹xd(t)。

2 控制器设计

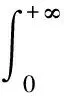
假设2 系统期望的状态轨迹xd(t)是连续的已知函数，且有界。

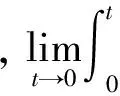
2.1 非线性逆控制器设计

定义跟踪误差e(t)=x(t)-xd(t)，如果系统的动态全部精确已知，并将外界干扰忽略，那么可设计非线性逆控制律如下形式：

(14)

其中，k为控制系数，将式(14)代入式(13)中，得

(15)

合理选择控制参数k，系统跟踪误差及其微分误差可趋于0，系统全局稳定。但高超声速飞行器的动态不能够精确获得。因此，系统的未建模动态和外界扰动是不能够忽略的。将F(x1，x2，t)、G(x1，t)分为标称部分、和不确定部分，即有如下关系式[20]

F(x1，x2，t)=F0(x1，x2，t)+ΔF(x1，x2，t)

(16)

G(x1，t)=G0(x1，t)+ΔG(x1，t)

(17)

2.2 基于自适应神经网络的输出反馈控制器

对系统的标称部分采用非线性逆的思想设计控制器，利用自适应神经网络来逼近不确定部分[21]。则可将实际控制输入写为如下形式：

U=u0(t)+ub(t)

(18)

其中，u0(t)为非线性逆控制器，形式为

(19)

将式(18)、式(19)代入式(13)，可得

(20)

利用式(15)的结果可将式(20)改写为

(21)

其中，η(x1，x2，U(t))为模型不确定部分，即

η(x1，x2，U(t))=ΔF(x1，x2，t)+ΔG(x1，t)U

(22)

将跟踪误差重定义为如下形式：

z(t)=[0，eT(t)]T

(23)

将上式求微分后，可写成如下形式：

B[η(x1，x2，U(t))+G0(x1，t)ub+d(t)]

(24)

其中

(25)

式(18)中的ub(t)设计为如下形式

ub(t)=G0-1(x，t)[un(t)+ul(t)]

(26)

式中un(t)为神经网络逼近器；ul(t)为鲁棒控制项，消除神经网络逼近误差影响[22]。

将状态变量x1、x2和延迟控制信号U(t-1)作为模型未知不确定项η的输入信号：

η(x1，x2，U(t-1))=W*TΦ(·)+ε[z(t)，U(t-1)]

(27)

式中W*为最优权重矩阵；ε(z(t)，U(t-1))为神经网络的重构误差；Φ(·)为高斯基函数向量。

假设3 为不失一般性，假设存在ξ(x)>0，使得‖ε(x)‖≤ξ(x)。

设计神经网络逼近器[23]为

(28)

将式(26)～式(28)代入到式(24)，可得

(29)

根据假设3可知，神经网络的逼近误差是有界的，且有‖ε[z(t)，U(t-1)]‖≤ξ[z(t)，U(t-1)]。

借鉴文献[24]的方法，假设存在矩阵P=PT>0，使得下面的近似黎卡提方程成立。

(30)

Q=QT>0是设定好的权重矩阵，R为正的增益矩阵，ζ为设定的常值。设计神经网络最优权重矩阵的自适应调节律为

(31)

式中Θ为自适应调节参数。

ul(t)设计为

ul(t)=um(t)+up(t)

(32)

其中，um(t)设计为

um(t)=ξ[z(t)，U(t-1)]sgn[BTPz(t)]

(33)

推论1um(t)采用变结构控制方法，符号函数为非连续函数，导致颤振现象，会对高超声速飞行器的作动器带来较大损害。因此，对变结构控制进行改进，设计为如下形式[24]：

(34)

其中，τ、σ为正的常数，且有

(35)

将up(t)设计为

up(t)=-R-1BTPz(t)

(36)

定理1 在满足假设1～3的情况下，系统式(13)在控制律式(18)、(19)、(26)、(28)、(32)、(34)、(36)的作用下，在自适应律式(31)调节下，能够保证跟踪误差在有限时间内收敛到0，且闭环系统的所有信号都是有界的。

稳定性证明:选择一个lyapunov函数为如下形式：

(37)

对上式lyapunov函数进行微分，并将式(29)、式(30)代入，可得

(38)

(39)

将式(34)代入下式，并结合假设3，可得

ε(z(t)，U(t-1))TBTPz(t)+um(t)TBTPz(t)≤

(40)

根据上述情况，可得到

(41)

将式(36)代入上式，整理可得

(42)

进一步整理，可得

(43)

t∈[0，T]，对上式两端求积分，可得

(44)

因为V(t)>0，所以有

(45)

根据假设1，可知

(46)

再根据引理1，可知跟踪误差z(t)收敛到0。

式(44)满足不等式：

(47)

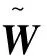
3 仿真验证

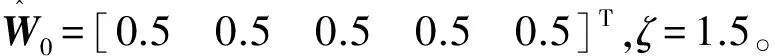
表1 气动力和力矩系数

图2～图4中飞行器的攻角、侧滑角和俯仰角可在较短的时间内跟踪期望轨迹。

图5～图7中角速度可很好地跟踪期望指令，说明设计的控制器可很好地克服系统中的不确定性以及外界扰动对系统的不利影响；同时，通过仿真结果可看出，攻角、侧滑角和速度滚转角可在较短的时间内实现精确跟踪，充分体现了设计的控制器能较好地满足高超声速飞行器实现快速姿态调整与跟踪的要求。另外，高超声速飞行器飞行跨度大，气动参数摄动剧烈。因此，将气动力和力矩系数进行了+50%摄动情况下进行了仿真。

图8～图10可知，因为气动力系数出现剧烈变化，攻角、侧滑角和滚转角在前3 s左右出现了较大的波动，但在第4 s左右开始能稳定地跟踪期望轨迹。图11～图13可知，在气动参数出现剧烈变化时，角速度在前几秒出现了较大的波动，但波动并不是很大，仍在可承受的范围内，且经过波动后，能趋于稳定。通过上述结果可说明设计的控制器能在气动参数出现剧烈变化，飞行器进行大跨度飞行时，实现姿态稳定控制。

4 结论

(1)传统的自适应控制、滑模控制难以处理系统中的非匹配不确定性，而神经网络逼近具有万能的逼近能力，可逼近任意不确定函数。所以，利用神经网络逼近系统的不确定性是非线性控制与智能控制的结合运用。但神经网络在进行逼近时会产生逼近误差，利用鲁棒项消除逼近误差对系统性能的影响，是两者相辅相成的突出表现。

(2)采用鲁棒项为滑模变结构形式，既消除了神经网络逼近误差的影响，又提高了系统的鲁棒性，且对其进行改进，避免了传统滑模控制带来的颤振现象。

(3)研究的Winged-Cone高超声速飞行器数学模型是美国兰利研究中心发布的，并公布了全套气动参数，此模型能深刻的描述系统的强耦合、强非线性等特点，具有就较大的研究价值和意义，是较理想的控制系统设计平台。

[1] Lohsoonthorn P,Jonckheere E,Dalzell S.Eigenstructurevs constrained design for hypersonic winged cone[J].Journal of Guidance,Control,and Dynamics,2001,24(4):648-658.

[2] Lind R.Linear parameter-varying modeling and control of structural dynamics with aerothermoelastic effects[J].Journal of Guidance,Control,and Dynamics,2002,25(4):733-739.

[3] Kuipers M,Mirmirani M,Ioannou P,et al.Adaptive control of an aeroelastic airbreathing hypersonic cruise vehicle[R].AIAA 2007-6326.

[4] Sigthorsson D O,Jankovsky P,Serrani A,et al.Robust linear output feedback control of an airbreathing hypersonic vehicle[J].Journal of Guidance,Control,and Dynamics,2008,31(4):1052-1066.

[5] Groves K P,Sigthorsson D O,Serrani A,et al.Reference command tracking for a linearized model of an air-breathing hypersonic vehicle[C]//Proc.of the AIAA Guidance ,Navigation and Control Conference and Exhibit.2005:6144-6158.

[6] Wang Q,Stengel R F.Robust nonlinear control of a hypersonic aircraft[J].Journal of Guidance,Control,and Dynamics,2000,23(4):577-585.

[7] Parker J T,Serrani A,Yurkovich S,et al.Control-oriented modeling of an air-breathing hypersonic vehicle[J].Journal of Guidance,Control,and Dynamics,2007,30(3):856-869.

[8] Fiorentini L,Serrani A,Bolender M A,et al.Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles[J].Journal of Guidance,Control,and Dynamics,2009,32(2):401-416.

[9] Xu H J,Mirmirani M,Ioannou P A.Robust neural adaptive control of a hypersonic aircraft[R].AIAA-2003-5641,2003.

[10] Wallner E M,Well K H.Nonlinear flight control design for the X-38 using CMAC neural networks[R].AIAA-2001-4042.

[11] Wu S F.Fuzzy logic based attitude control of the spacecraft X-38 along a nominal re-entry trajectory[J].Control Engineering Practice,2001,21(9):699-707.

[12] Marrison C,Stengel R F.Design of robust control systems for a hypersonic aircraft[J].Journal of Guidance,Control and Dynamics,1998,21(1):58-63.

[13] 宋超,赵国荣,李海君.临近空间高超声速飞行器自适应反演滑模控制[J].弹箭与制导学报,2012,32(3):49-52.

[14] Huo Y,Mirmirani M,Ioannou P A,et al.Altitude and velocity tracking control for an airbreathing hypersonic cruise vehicle[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Colorado:AIAA:2006,1305-1315.

[15] Xu H J,Ioannou P A,Mirmirani M.Adaptive sliding mode control design for hypersonic flight vehicle[J].Journal of Guidance,Control and Dynamics,2004,27(5):829-838.

[16] Keshmiri S,Mirmirani M D.Six-DOF modeling and simulation of a generic hypersonic vehicle for conceptual design studies[R].AIAA 2004-4805.

[17] Shaughnessy J D,Pinckney S Z,McMinn J D,et al.Hypersonic vehicle simulation model:winged-cone configuarion[R].NASA TM-102610,1990.

[18] 陈洁.近空间高超声速飞行器非线性控制方法研究[D].烟台:海军航空工程学院,2009.

[19] Hamed Kebriaei ,M Javad Yazdanpanah.Robust adaptive synchronization of different uncertain chaotic systems subject to input nonlinearity[J].Commun Nonlinear Sci Numer Simulat,2010,15(3):430-441.

[20] Fayez F M El-Sousy.Adaptive hybrid control system using a recurrent RBFN-based self-evolving fuzzy-neural-network for PMSM servo drives[J].Applied Soft Computing,2014,25(21):509-532.

[21] Labus J,Hernández J A,Bruno J C,et al.Inverse neural network based control strategy for absorption chillers[J].Renewable Energy,2012,39(5):471-482.

[22] Mohsen,Farahani.Intelligent control of SVC using wavelet neural network to enhance transient stability[J].Engineering Applications of Artificial Intelligence,2013,13(26):273-280.

[23] Singh H P, Sukavanam N.Simulation and stability analysis of neural network based control scheme for switched linear systems[J].ISA Transactions,2012,51(24):150-110.

[24] Peng Jin-zhu,Rickey Dubay.Nonlinear inversion-based control with adaptive neural network compensation for uncertain MIMO systems[J].Expert Systems with Applications,2012,39(25):8162-8171.

(编辑：吕耀辉)

Adaptive neural network controller design for hypersonic vehicle

ZHAO He-wei，HU Yun-an，LIANG Yong，YANG Xiu-xia

(Department of Control Engineering，Naval Aeronautical and Astronautical University，Yantai 264001，China)

A nonlinear inversion-based controller with adaptive neural network compensation was designed for a class of hypersonic vehicle in the case that vehicle’s nonlinear model comprises of nonlinear unknown uncertain function caused by unmodeled dynamics,aerodynamic parameter variation and unknown external disturbances were fully considered.Firstly the dynamic characteristics of system were separated as two components:a nominal component and an uncertain component.The controller for the nominal component was designed based on nonlinear inversion control scheme,and uncertain component was approximated by the neural network.The optimal weight matrix was adjusted by adaptive learning law to improve the online approximated capability of neural network.The modified variable structure controller was designed for eliminating the effects of the neural network approximated errors.The controller can guarantee that the tracking error converges to zero and all signals of closed loop system are bounded.The simulation results demonstrate the rightness of the proposed schemes.

hypersonic vehicle；adaptive；neural network；variable structure control

2016-07-12；

2016-09-15。

航空基金(20140184001)；中国博士后基金(2015M572693)。

赵贺伟(1985—)，男，博士生，主要研究方向为非线性控制、自适应控制等。E-mail：www.zhwsdyt@163.com

V448

A

1006-2793(2017)02-0257-07

10.7673/j.issn.1006-2793.2017.02.022