BDS 13号卫星星载原子钟在轨特性分析

崔博斌，黄观文，李平力，王 乐

长安大学地质工程与测绘学院，陕西 西安，710054

1 引 言

全球卫星导航系统作为支撑空天地一体化的主要信息来源之一，其卫星服务性能直接影响时空基准质量和精度，而星载原子钟作为星上核心部件，其特性与稳定度直接决定卫星服务能力[1-11]。我国自主研发的北斗卫星导航系统(BDS)，自2012年12月17日起公开对亚太区域提供定位、导航、授时(PNT)服务。现阶段BDS由三种异构星座组成[1-5]，分别为地球同步轨道卫星(GEO)、倾斜地球同步轨道卫星(IGSO)和中圆地球轨道卫星(MEO)。不同轨道卫星存在不同的运动周期与在轨特性，其星载原子钟在轨服务能力及差异性是关注热点。

目前部分学者针对BDS不同星座卫星钟在轨特性进行了整体分析评估，得出了有价值的结论[2-5，11]。然而北斗在轨卫星中，C13号卫星相对特殊，其在运行期间由于某些原因，于2014年底停止提供服务，2016年10月12日将原C15号卫星改变为编号C13号卫星继续提供服务，自此C13号卫星轨道由原先所在的MEO轨道变更为原C15卫星所在的IGSO轨道。BDS区域几何构型也由设计最初的5颗 GEO、5颗 IGSO、4颗MEO，变为 5颗 GEO、6颗 IGSO、3颗 MEO卫星[12，13]。因此，原C13卫星停止服务前是否出现性能异常?变换前后星载原子钟在轨特性是否发生显著差异?目前C13卫星钟是否具备稳定服务能力等问题引起关注。但已有文献缺少对其针对性的研究，基于此，本文对C13卫星变换前后的星载原子钟相位、频率、频漂及拟合残差和频率稳定度指标进行了评估分析，利用GBM精密钟差产品计算了星载钟特性指标并评价了现阶段的在轨服务性能。

2 卫星钟差数学模型

2.1 粗差探测方法

通过卫星的钟差数据可以评估分析其在轨特性与服务质量，但卫星原子钟在轨运行会受到多种噪声因素干扰而产生异常数据，这对于其特性分析影响显著，因此，需要进行粗差的识别与剔除。本文采用中位数法(MAD)进行粗差探测[3]，考虑到精密钟差由精密定轨与时间同步法求得，而轨道皆以单天解或三天解解算，并以天为单位提供精密文件，因此，将精密钟差数据中天文件完整弧段为一个单位进行粗差识别与剔除。首先提取出卫星钟差相位序列，通过升序或降序排列求取其中位数为m，将求取的中位数分别与相位数据进行作差获取差值序列;然后将差值序列以一天为完整弧段进行升序或者降序排列，求取其中位数为MAD，此时MAD即为精密钟差数据一次差序列的中位数，通过一次差可以放大粗差与异常值更易于探测;最终将MAD分别与差值序列进行粗差检核，当差值序列中数值大于n倍的中位数MAD时即判定为粗差，将对应的历元相位值赋为零并标记出，当序列完成检核后通过拉格朗日插值获取标记位缺失的钟差序列。中位数MAD可表示为：

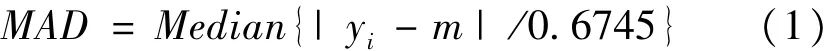
式中，m为时间序列的中间数，即 m=Median{yi};当观测量|yi|＞(m+n·MAD)时(本文整数n取3)，大于就认为是粗差点。

2.2 卫星钟差拟合模型

在对卫星钟差进行建模时，由于卫星钟的相位(a0)、频率(a1)和频漂(a2)是反映其物理特性的三个参数，因此，采用二次多项式拟合并预报卫星钟差模型，进而分析卫星钟的相位、频率、频漂特性规律。二次多项式钟差拟合模型如下[4]：

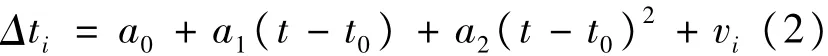
式中，a0、a1、a2为相位、频率和频漂;t为所需拟合预报的时刻;t0为星钟参数的参考历元;Δti为钟差相位观测值;vi为拟合残差。

2.3 卫星钟稳定度分析模型

频率稳定度是表征卫星钟特性的一个重要指标，可以描述频率受噪声影响的随机起伏情况及卫星星载原子钟稳定特性[3]。目前，BDS工作卫星均配备国产Rb原子钟，由于Rb钟具有明显的频漂，而且平滑时间过长还会受到甚低频噪声影响，因此，采用置信度较高的哈达玛方差[6-8]来描述Rb钟的频率稳定性。对于频率数据序列{yn，n=1，2，…，M}，其采样间隔为τ0，M为采样个数，则基于频率数据的哈达玛方差可表示为[5]

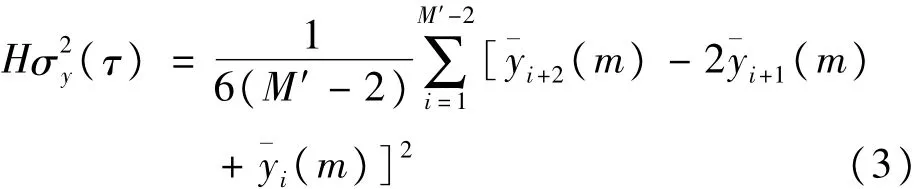
式中，τ=mτ0为平滑时间;m为平滑因子，一般取的个数，且M′=为第i个平滑时间τ内m个频率数据的均值，即相应的相位数据序列为{xn，n=1，2，…，N}，N为相位数据个数，且N=M+1。可得到基于相位数据的哈达玛方差：

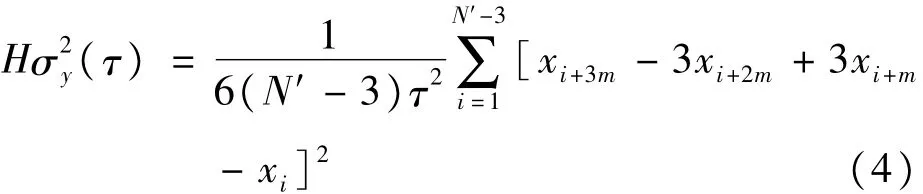
式中，τ为xi的平滑时间;N′为测量间隔τ的相位数据个数，N′=int(N/m)+1;通过对采样间隔为τ0的相位数据每个测量间隔τ取一个值获得。由于对频率数据进行了两次差分，对相位数据进行了三次差分，因此，哈达玛方差对线性频漂不敏感。

3 卫星在轨工作状态

C13号卫星自2016年10月12日始由C15号卫星更换编号为C13号卫星并再次提供服务，轨道由原先13号卫星的MEO星座变换为IGSO星座，星载钟的运行周期及在轨特性都受到影响。为了具体分析BDS 13号卫星的星载钟在轨性能，本文统计了BDS各颗卫星的在轨工作状态如图1所示[13]。

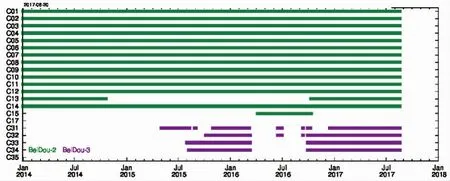
图1 BDS卫星在轨状态统计

从图1可以看出，BDS 13号卫星在运行一段时间后出现异常并停止服务，后期由C15号卫星转为C13号卫星并继续提供服务，具体变更信息见表1[13]。

表1 C13号卫星运行状态统计

通过表1可以看出，C13号卫星后期由C15号卫星替换运行于IGSO轨道，2016年10月11日更替完成并提供服务，而现在更换后的C13号卫星已在轨运行了近17个月，对于C13卫星星载原子钟目前的特性分析与评估显得尤为重要。

4 钟差特性分析

为了分析评估C13号卫星的特性与星载钟性能，本文选取了德国地学研究中心(GFZ)2013年1月1日至2017年8月15日的GBM精密钟差产品，评估更换前后卫星的原子钟特性差异。经过钟差数据预处理后，通过二次多项式拟合获取的星载钟相位、频率和频漂如图2所示。

图2 C13号卫星相位(上)、频率(中)、频漂(下)

从图2可以看出，原先C13号卫星星载原子钟在轨表现出两种不同的相位及频偏特性，卫星在轨的星载原子钟发生了切换，频漂一直保持着一个较为稳定的精度，但存在着一个明显的漂移率。原C13号卫星在轨经过了两次调相和一次星载钟切换，但切换过后钟差精度有了较大幅度的提升。而卫星更替前后频漂存在着较大区别，新变换的IGSO卫星原子钟频漂偏大，相位与频率无显著变化。为了进一步分析卫星更替后的卫星钟特性，单独给出变更后的C13星载钟相位、频率和频漂，数据采用2016年10月12日至2017年8月15日的GBM精密钟差产品，如图3所示。

通过图3中相位、频率和频漂序列可以看出，更换后C13号卫星经过一次星载原子钟切换和一次调频后逐步趋于稳定，在第一次调整时星载钟发生了切换，相位数据与频率数据发生了较大变化。频漂序列则由更换初期存在一个显著的系统偏移，通过切换另一个星载原子钟后，频漂逐渐趋于平稳，这也表明C13卫星钟经过适当在轨调整后卫星钟参数已趋于稳定，新切换的原子钟精度与特性优于切换前的原子钟。

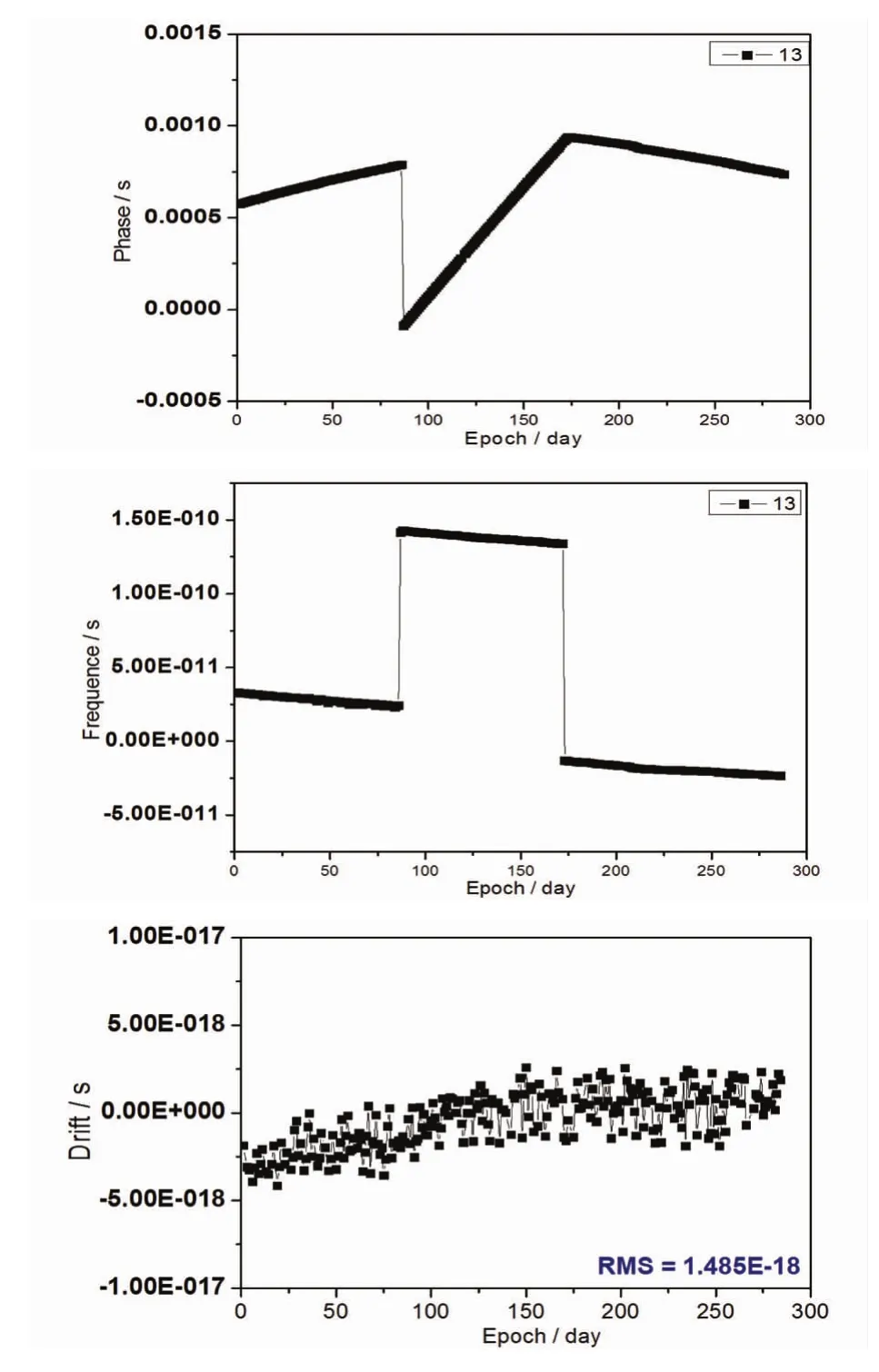
图3 C13号卫星更换后相位(上)、频率(中)、频漂(下)

5 星载原子钟频率稳定度分析

二次多项式拟合除了可以获取卫星钟差的相位、频率和频漂系数外，还可以获得拟合模型的残差精度指标。拟合残差的精度可在一定程度上反映出此卫星在用户实时导航定位中的卫星钟差预报能力。图4统计了C13于2013年1月1日至2017年8月15日，在卫星变更前后经过二次多项式拟合后的模型残差序列。

从图4可以看出，C13星载钟原先拟合精度较差，残差波动大，经过主备钟切换后(左侧分界线)，其拟合精度大幅提升，并保持着一个较为优异的精度。在卫星出现故障后，C15号卫星改变编号为C13号卫星并开始提供服务，但初期其星载钟拟合精度仍然较差，经过2017年1月20日主备钟切换(右侧分界线)，拟合残差精度显著提升，并稳定于10E-9级别。从数值上看，MEO卫星钟拟合精度优于IGSO结果，但几何构型带来的影响远小于卫星钟自身特性差异。

图4 C13号卫星二次多项式拟合残差序列

考虑到相位数据波动较大，而频率稳定度可以更为准确描述星载原子钟特性优劣程度，本文采用哈达玛方差求取钟差频率稳定度指标。计算统计了C13号卫星天稳定度结果序列如图5(左)所示，时间为2013年1月1日至2017年8月15日。同时统计了C13号卫星更换后卫星钟稳定度序列如图5(右)所示，时间为2016年10月12日至2017年8月15日。为了从数值上对比，统计了卫星更换前后十个月的频率稳定度数据见表2。

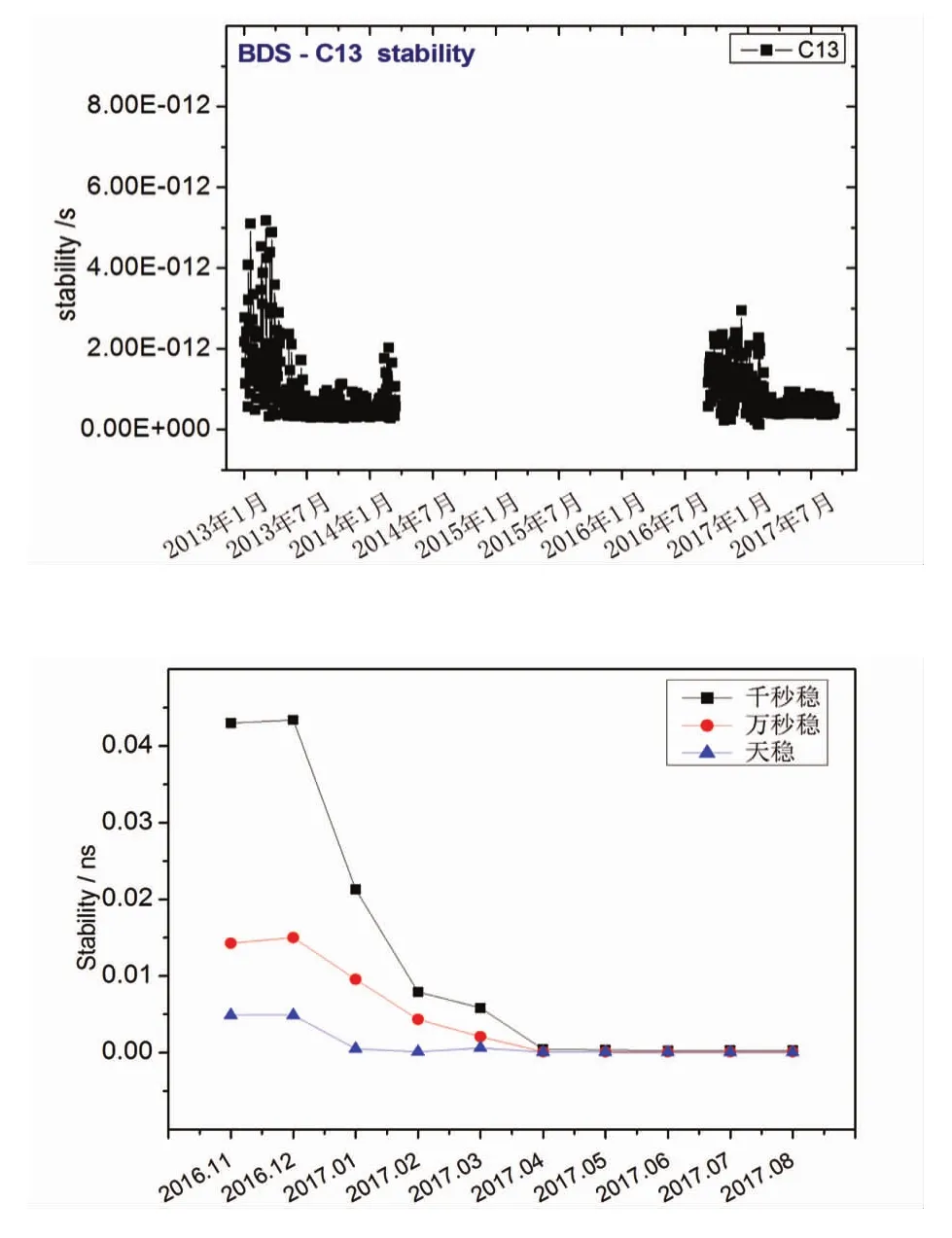
图5 C13号卫星稳定度趋势图

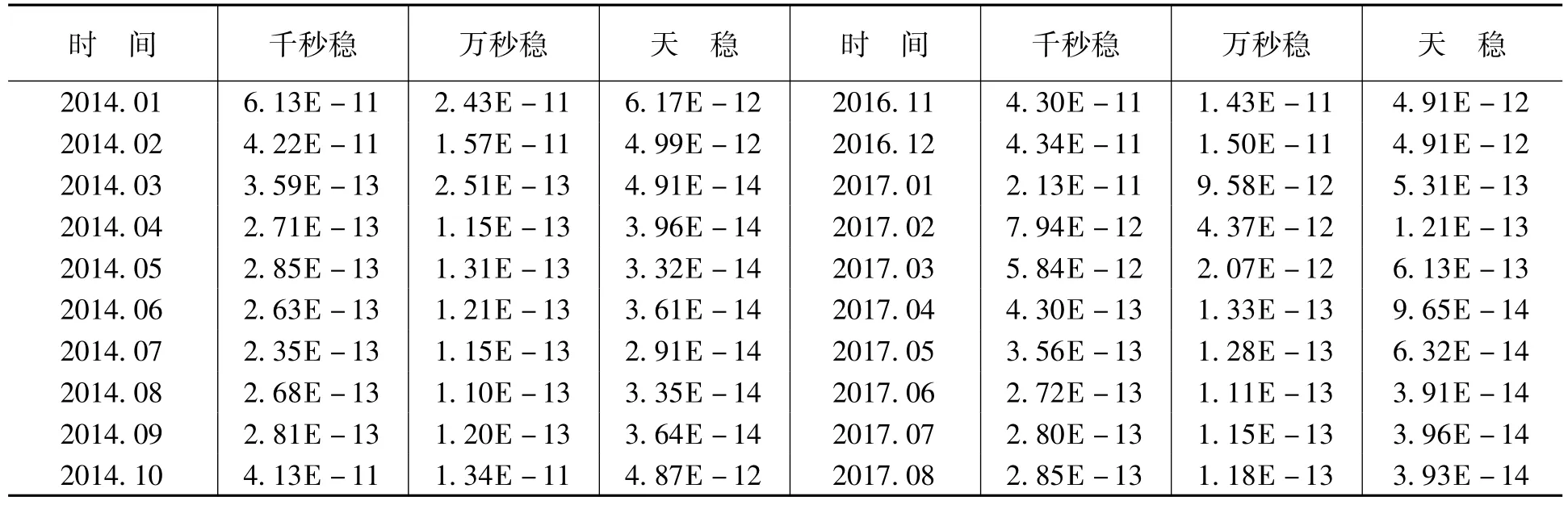
表2 C13号卫星稳定度统计

通过图5及表2中千秒稳、万秒稳及天稳定度结果序列可以看出，BDSC13卫星在更换前卫星初始入轨时频率稳定度较差，经过星载钟在轨调整与主备钟切换后性能逐步趋于稳定(图5蓝色虚线标识处)，但在2014年1月后频率稳定度突然增大(图5绿色虚线标识处)，表明星载原子钟出现异常。而更换后的卫星钟初始时刻稳定度较大，但经过星载原子钟切换和在轨调频后(图5红色虚线标识处)，频率稳定度由逐渐增大变为小范围内平稳波动。通过图5中频率稳定度可以看出，切换后的星载原子钟千秒稳可达到2.8E-13s，万秒稳达到1.1E-13s，天稳达到1.9E-14s，显著优于切换前提供服务的原子钟，表明不同星载原子钟其自身的精度与稳定特性对于钟差的特性与服务质量影响远大于环境影响，而对比卫星更换前后的稳定度指标序列，可以看出MEO稳定度指标优于IGSO卫星指标。经过在轨星载原子钟调整切换，现阶段C13号卫星已能够提供正常服务，各项特性指标均已达到了设计指标要求。

6 总 结

通过对BDS C13号卫星钟差数据进行特性分析，获取了其相位、频率、频漂及拟合残差与稳定度的长期指标序列，并对编号更换前后的C13号卫星原子钟特性和质量进行了评估分析。结果表明，更换后的C13号卫星经过在轨调整与星载原子钟切换，其频漂、拟合残差和稳定度等都已趋于稳定，现阶段卫星原子钟已达到设计精度要求，能够提供稳定可靠的导航定位服务。

[1]杨元喜，李金龙，王爱兵等.北斗区域卫星导航系统基本导航定位性能初步评估[J].中国科学：地球科学，2014，44(1)：72-81.

[2]郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D].郑州：信息工程大学，2006.

[3]黄观文，杨元喜，张勤.开窗分类因子抗差自适应序贯平差用于卫星钟差参数估计与预报[J].测绘学报，2011，40(1)：15-21.

[4]黄观文.GNSS星载原子钟质量评价及精密钟差算法研究[D].西安：长安大学，2012.

[5]付文举.GNSS在轨卫星钟特性分析及钟差预报研究[D].西安：长安大学，2014.

[6]Senior K L，Ray JR，Beard R L.Characterization of Periodic Variations in the GPS Satellite Clocks[J].GPS Solutions，2008，12(3)：211-225.

[7]郭海荣，杨元喜.导航卫星原子钟时域频率稳定性影响因素分析[J].武汉大学学报·信息科学版，2009，34(2)：218-221.

[8]Howe D.The Total Deviation Approach to Long-term Characterization of Frequency Stability[J].IEEE Transactions on Ultrasonics Ferroelectrics&Frequency Control，2000，47(5)：1102-1110.

[9]杨赛男，陈俊平，张益泽等.基于最小二乘频谱分析的GPS/GLONASS卫星钟差特性研究[J].大地测量与地球动力学，2014，34(2)：169-174.

[10]Huang GW，Zhang Q，Fu W J，et al.Quality Variation of GPSSatellite Clocks On-orbit Using IGSClock Products[J].Advances in Space Research，2013，51(6)： 978-987.

[11]黄观文，余航，郭海荣等.北斗在轨卫星钟中长期钟差特性分析[J].武汉大学学报·信息科学版，2017，42(7)：982-988.

[12]Helmholtz-Zentrum Potsdam.GFZGerman Research Centre for Geosciences[OL].[2018-01-03].ftp：//ftp.gfzpotsdam.de/pub/GNSS/products/mgnss

[13]International GNSSMonitoring&Assessment System[OL].[2018-01-03].http：//www.igmas.org