基于地磁矢量数据的日变模型构建及精度分析
孙 广,王兴涛,郭美军,李双钦,翟 伟
1.地理信息工程国家重点实验室,陕西 西安,710054;
2.西安航天天绘数据技术有限公司,陕西 西安,710054;
3.西安测绘研究所,陕西 西安,710054
1 引 言
地球磁场主要由主磁场、岩石圈磁场、变化磁场和感应磁场组成,在利用地面台站的地磁观测资料分析地磁场主磁场的空间分布,或是分析岩石圈磁场变化异常时,都需要去除变化磁场和感应磁场所产生的影响[1]。日变化磁场中外源场占主要比重,外源场主要起源于地球外部,该场的变化与太阳活动有着紧密的关联[2],外源场变化主要表现为短期变化,其变化的程度是有限的,且地球变化磁场具有一定的混沌特性[3]。由于地磁日变化对地磁观测影响较大,在进行实际测量中,必须进行扣除。通过构建日变模型预报日变值,对原始地磁数据进行日变改正,可提高地磁数据的精度。
在日变模型构建研究方面,有学者利用等效电流体系模型,通过电流正演地磁变化构建日变模型[4],该模型精度较好。目前,日变模型的构建方法主要有多项式、曲线拟合等方法[5-6],还有学者采用加权平均法[7]和反距离加权插值法[8]进行日变数据处理。本文针对地磁台站矢量数据采用傅里叶频谱分析进行日变模型构建,并对所构建模型的精度进行分析。
2 地磁日变模型
构建地磁日变模型,首先需要计算地磁观测数据的日变数据,而日变数据需要计算日变基值,然后与观测数据求差得到日变数据,最后根据获取到的日变数据进行傅里叶建模。
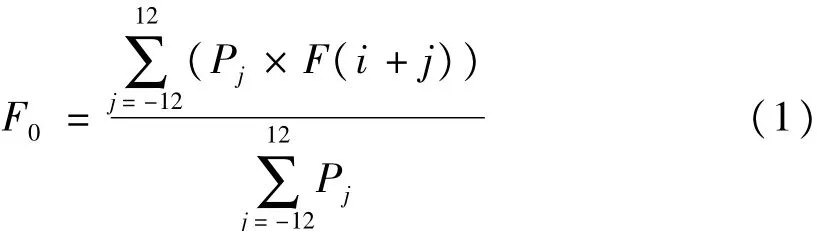
式中,F0为日变基值(nT);F(j)为日变站j点对应的观测值(nT);Pj为Gaussian滤波器系数,计算系数值固定;i为当前计算滤波点位置;j为参与滤波计算点的位置,本文以12阶滤波器为例进行计算。
滤波器系数计算公式如下:
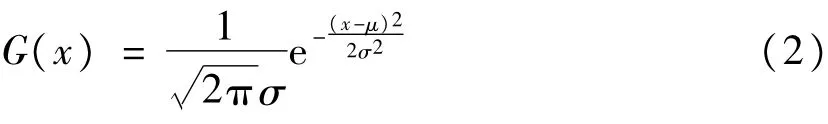
其中,x表示点位坐标;μ为0;σ为Gaussian分布的标准差,可利用多天子夜2小时观测数据的标准差取平均值获得。
通过日变基值可计算得到日变数据,对日变数据进行傅里叶分析,以总强度F、水平分量H、磁偏角D以及磁倾角I为例,选择有限个频点进行傅里叶建模,模型计算如下式:
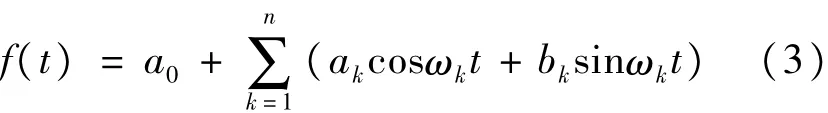
本文利用最小二乘法估计(3)式中的系数ak、bk,考虑到运算量,分别以4个、6个、8个频点为例进行建模分析。
最小二乘估计的公式为

令:
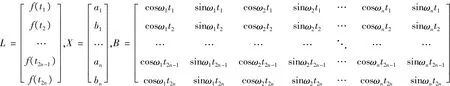
其中,f(ti)为t点对应观测值。可以通过(4)式求解系数矩阵X,即为模型系数,进而可以构建地磁日变模型。
3 实验分析
由于地磁观测值受地磁环境指数Kp的影响,选取地磁活动平静时间的日变数据能够获得更高精度的日变模型。根据这一原则,本文选取BMT台站2010年1月连续5天的日变数据(Kp指数平均值为3.4),以日变数据中的总强度F、水平分量H、磁偏角D以及磁倾角I为例进行计算,日变数据曲线如图1所示。计算日变数据的日变基值分别为总强度 F:54953.7nT,水平分量 H:28511.3nT,磁偏角 D:0.132203rad,磁倾角 I:1.02532rad。
这两句话是关于两组实验结果的对比结论,通过重复动作的实施对象:their partners,达到强调的效果,也有效地将两句话之间的对比关系凸显出来。动物学是一门主要以实践和研究为主的学科,在叙述实验过程和结果时,常要重复使用实验中的实验对象,条件等相关词汇,用以表示强调。因此,在动物学英语语篇中经常会大量使用重复的词汇衔接手段来突出主题。
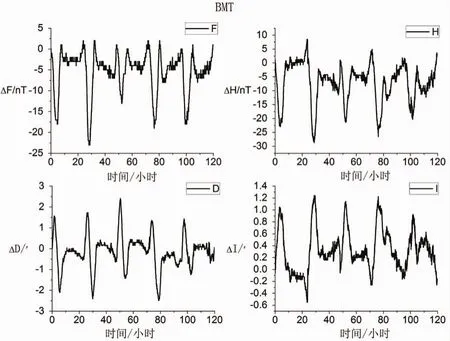
图1 BMT四要素连续5日日变观测数据曲线
从图1可以看出日变数据峰值基本出现在每天中午前后,且呈现明显的周期性,符合傅里叶变化的特性。对图1中四要素的日变数据进行傅里叶变换,可得频谱如图2所示。
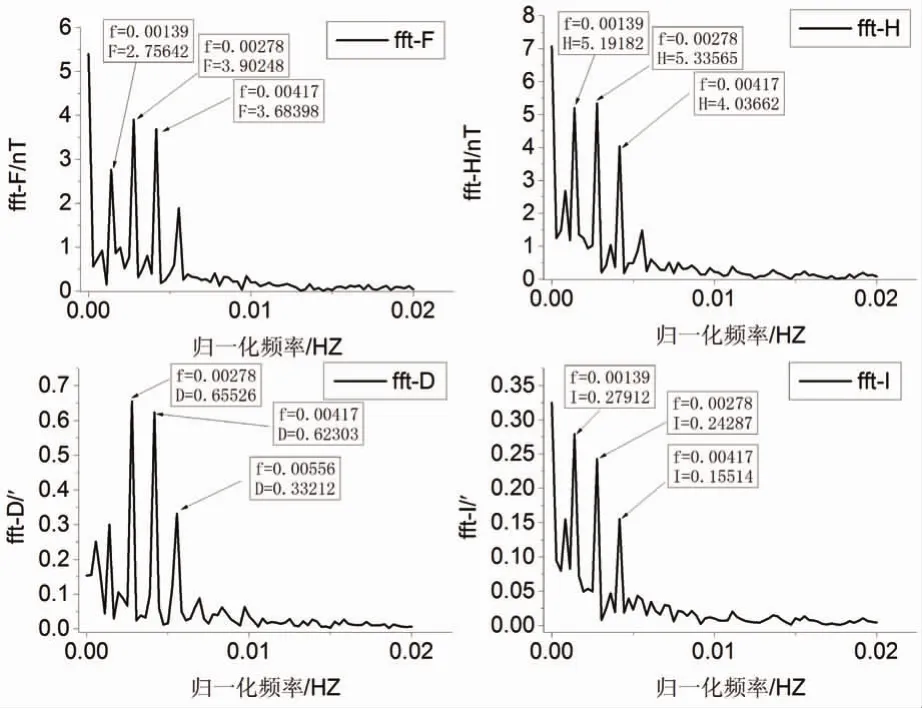
图2 BMT台站四要素频谱图(0~0.02Hz)
由图2可以看出四要素的频谱基本相同,能量主要集中在归一化频率0.01Hz以内,在归一化频率下以4到8个频点为例进行傅里叶建模,并统计模型拟合精度。
3.1 模型精度分析
利用图1中的日变数据,分别以4点、6点及8点为例建模,并对模型的计算精度进行统计。通过最小二乘法估计系数ak和bk的值,对模型与实测的日变数据进行对比,由于篇幅原因,只列出4点建模曲线拟合对比图,如图3所示。
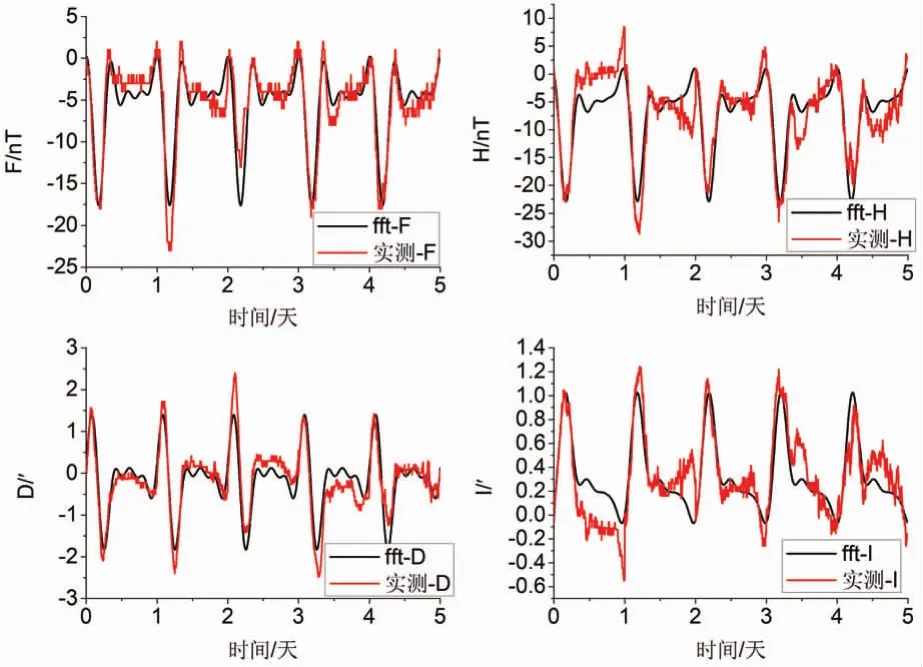
图3 BMT台站四要素4点fft模型与实测数据对比
由图3可以看出4点傅里叶模型总强度F、磁偏角D与实测数据拟合性较好,水平分量H、磁倾角I拟合精度较差。为进一步量化模型的拟合精度,对不同地磁要素模型计算值与实测结果的差值进行统计,见表1。

表1 BMT站模型5天计算数据与实测数据残差分析
从表1中的统计数据可以看出,建模点数的增加可以提高模型拟合的精度,总强度F的RMS提高了约0.27nT,水平分量H的RMS提高了约0.54nT,磁偏角D的RMS提高了0.04′,磁倾角I的变化不大。
为了验证上述5天日变数据建模的可靠性,采用连续10天的日变数据进行模型构建,并与实测数据进行对比,拟合精度结果见表2。
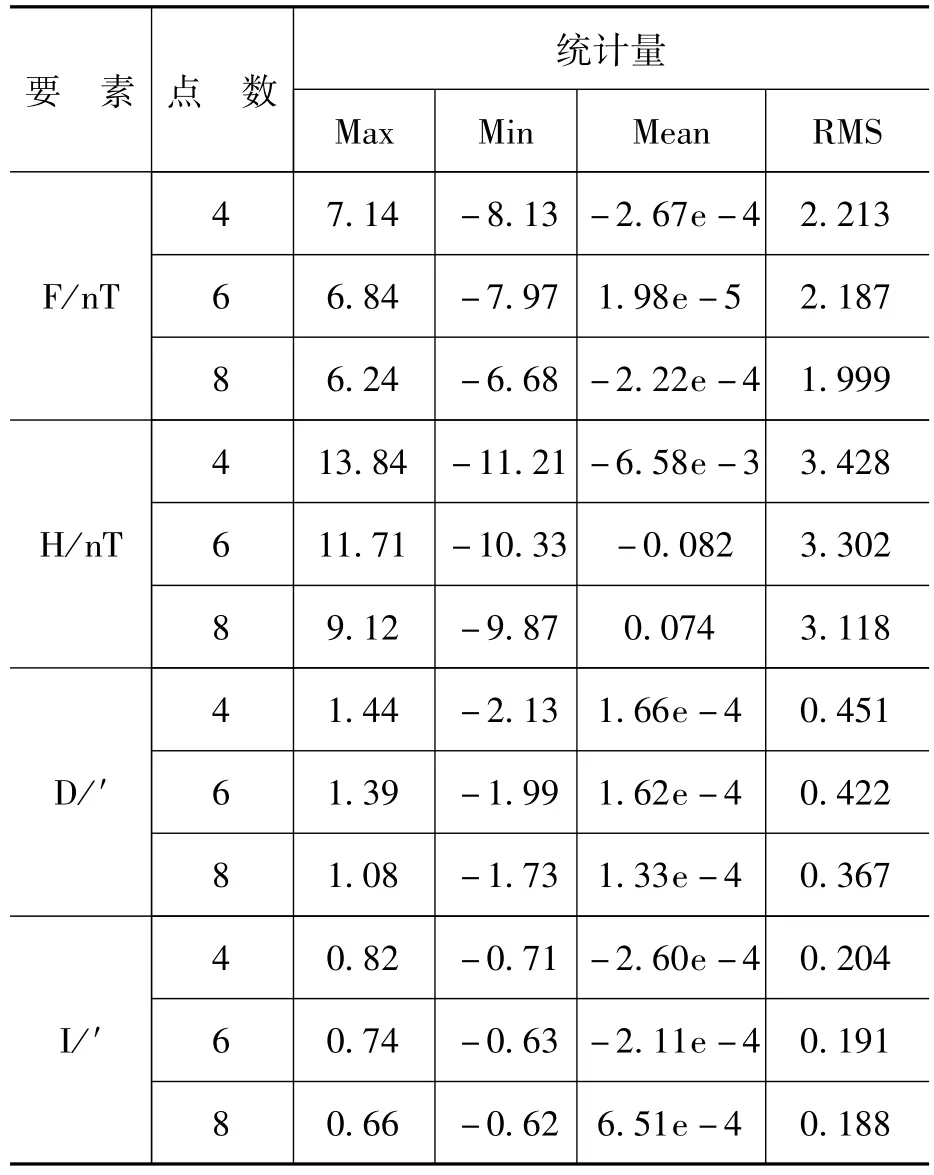
表2 BMT站10天数据模型计算数据与实测数据残差分析
从表2中可以看出,利用连续10天的数据所构建的模型比连续5天观测数据构建模型的精度稍差,用4点、6点、8点的拟合精度总强度F分别下降了0.215nT、0.19nT、0.275nT。 这是由于 Kp指数变化较大,其中后5天中有2天的Kp指数分别为6.8和7.4,地磁干扰较强,影响了日变数据的精度,从而降低了日变模型的精度。
3.2 模型外推分析
构建日变模型是为了对地磁日变值进行预报,所以需要对不同点数构建的模型进行外推分析。以外推1天为例,由于四要素的外推结果基本相同,因此只列出了总强度F在不同点数建模的外推计算曲线,如图4所示。
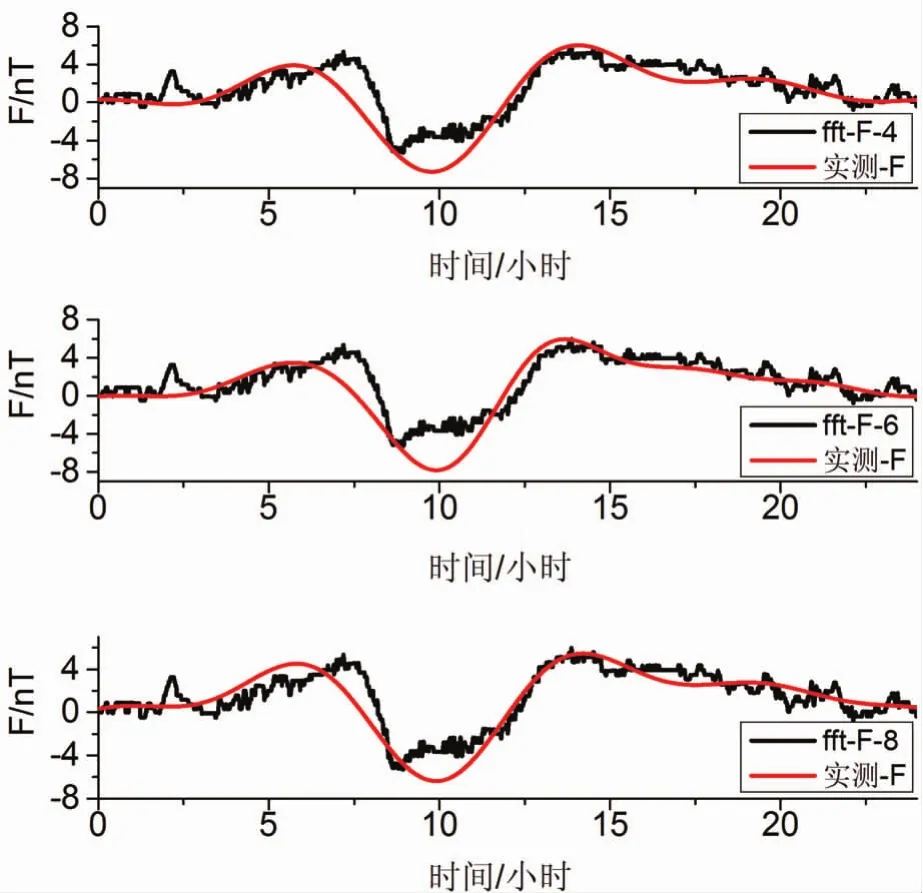
图4 BMT台站总强度fft模型与实测数据对比
由图4的预测曲线可以看出,外推后的计算结果与实测数据的差值较小,通过观察实测数据可发现,实测数据的波动性基本与前几日保持一致,外推1天的地磁环境与模型较为接近,所以曲线符合较好。
为验证模型的外推精度,分别将构建的日变模型外推1天、2天、3天(见表3~5),并外推到不同季节5月、8月、12月(见表6~8),对总强度F、水平分量H、磁偏角D、磁倾角I的模型预测结果进行误差统计。
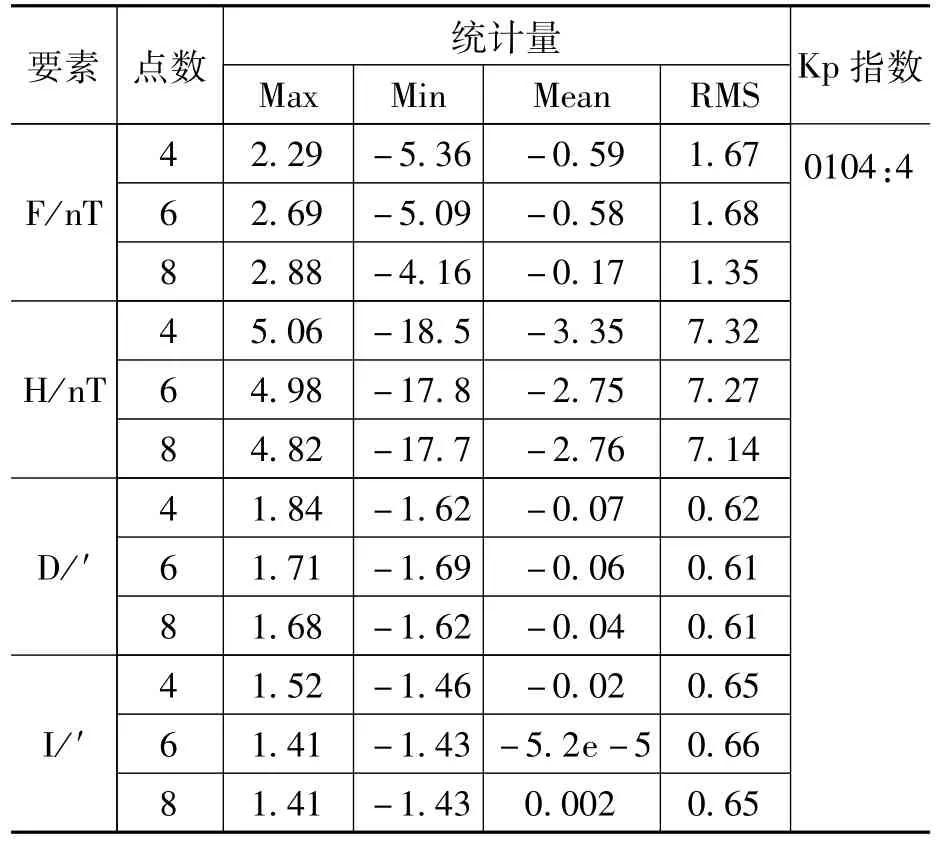
表3 BMT站模型外推计算数据与实测数据残差分析(1天)

表4 BMT站模型外推计算数据与实测数据残差分析(2天)
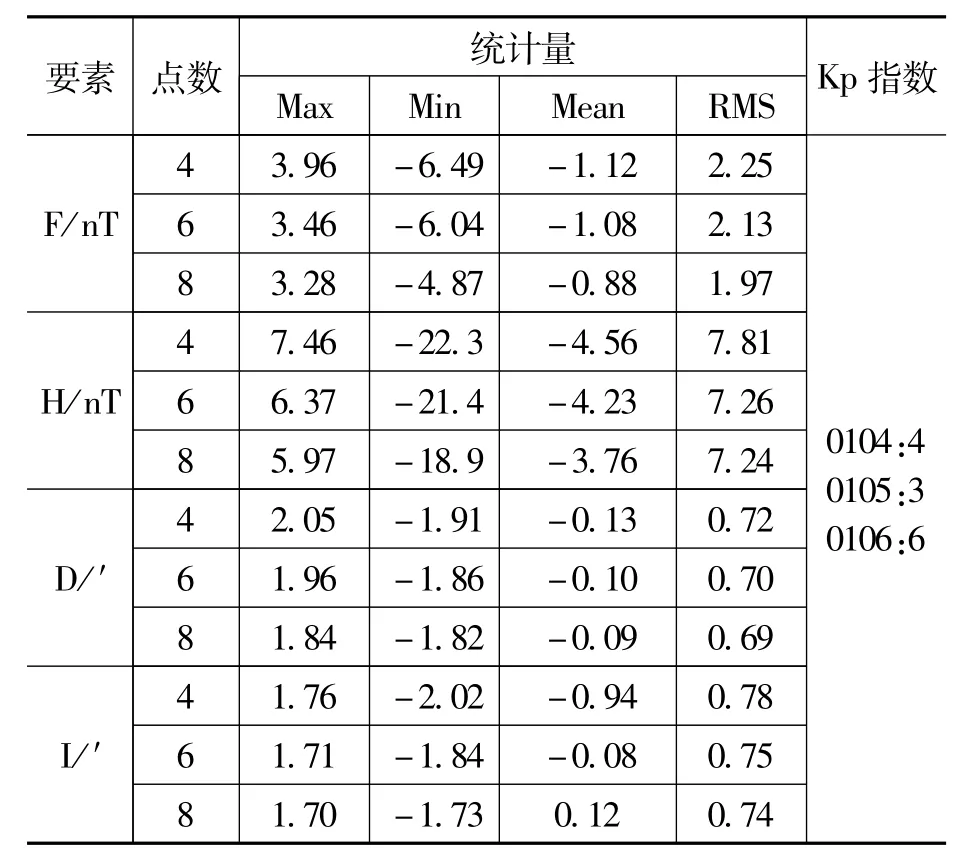
表5 BMT站模型外推计算数据与实测数据残差分析(3天)
从表3中可以得出,外推1天总强度F的RMS在1.68nT以内,水平分量 H的 RMS在7.32nT以内。为进一步验证模型的外推精度,分别将模型外推至2天、3天,计算预报日变值,与实测的日变值进行比较。从表4、5中可以看出,外推2天总强度F的RMS在1.76nT以内,水平分量H的RMS在7.79nT以内,相比较外推1天RMS精度总强度 F、水平分量 H分别下降了0.09nT、0.47nT,精度变化不大;外推3天的总强度F、水平分量 H的 RMS精度分别在2.25nT、7.81nT,与外推1天相比,总强度F、水平分量H分别下降了0.58nT、0.49nT,总强度F的精度变化较大。所以外推1天,日变值精度最高。
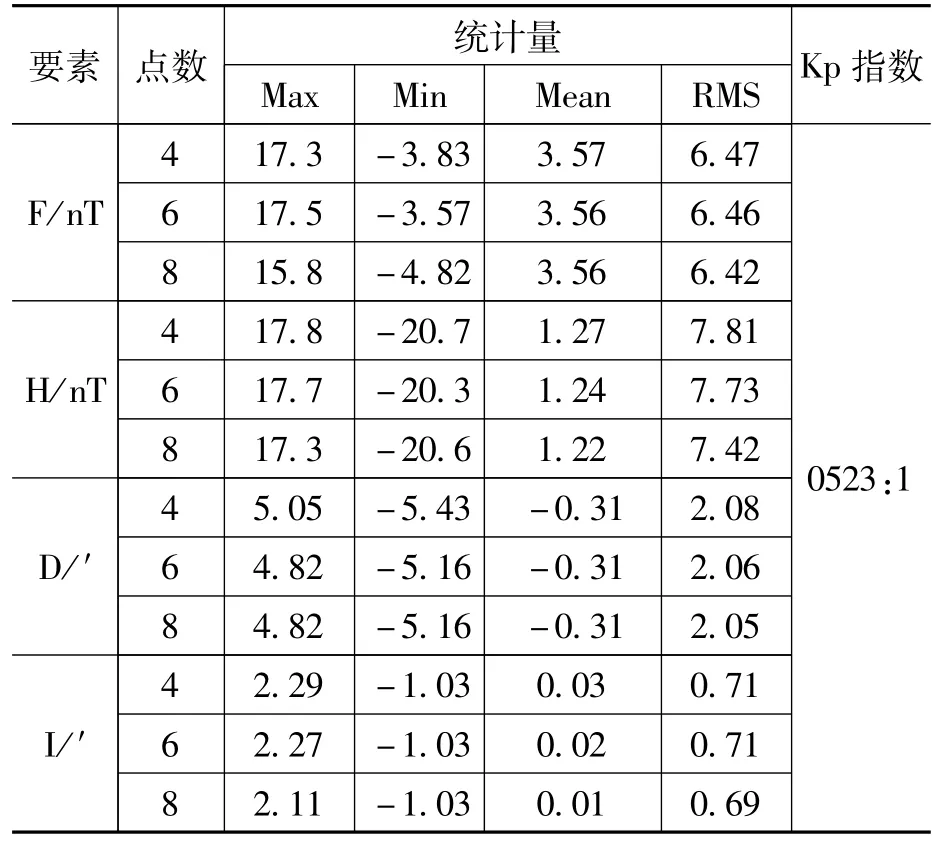
表6 BMT站模型外推计算数据与实测数据残差分析(5月)
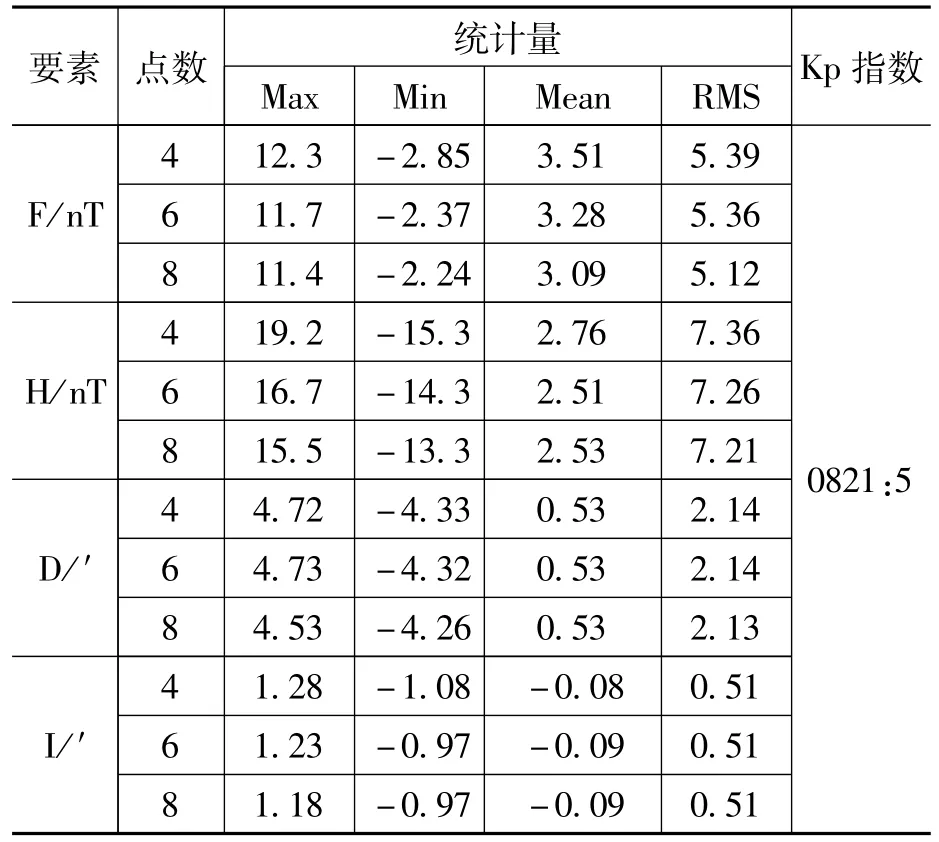
表7 BMT站模型外推计算数据与实测数据残差分析(8月)
从表6、7可以看出,大时间跨度的外推,模型精度下降较大。5月份总强度F的RMS在6.5nT以内,水平分量H在7.9nT以内;8月份总强度F的RMS在5.4nT以内,水平分量H在7.4nT以内。这是由于建模数据与5月、8月观测数据的地磁环境指数差异较大,所以模型精度较差。表8中,12月与1月地磁环境接近,所以各地磁要素的RMS精度较好,这表明日变模型精度受地磁环境影响较大。

表8 BMT站模型外推计算数据与实测数据残差分析(12月)
4 结束语
本文对BMT地磁台站连续5天的日变数据进行傅里叶分析,得到了日变频谱特性,最后利用傅里叶变化进行日变模型构建。模型分析结果表明,利用傅里叶变化构建的日变模型可以进行磁偏角D、磁倾角I的日变预报,并且短时间内的精度最优,而总强度F和水平分量H预报精度较差。所以,日变模型仅适合地磁要素的短时间外推计算。
[1]徐文耀.地球电磁现象物理学[M].合肥:中国科学技术大学出版社,2009.
[2]王晶,冯学尚.日冕物质抛射引起地磁扰动的分类预报[J].物理学报,2007,56(4):2466-2474.
[3]牛超,李夕海,刘代志.地球变化磁场Z分量的混沌动力学特性分析[J].物理学报,2010,59(5):3077-3087.
[4]赵旭东,杜爱民等.Sq电流体系的反演与地磁日变模型的建立[J].地球物理学进展,2010,25(6):1959-1967.
[5]边刚,夏伟,金绍华等.利用最小二乘拟合法进行多站地磁日变基值归算[J].地球物理学报,2015,58(4):1284-1289.
[6]单汝俭,金国,曾志成.局部地区地磁日变及拟合方法研究[J].长春地质学院学报,1990,20(3):315-322.
[7]边刚,刘雁春,卞光浪等.海洋磁力测量中多站地磁日变改正值计算方法研究[J].地球物理学报,2009,52(10):2613-2618.
[8]顾春雷,张毅,徐如刚等.基于虚拟日变台进行地磁矢量数据日变通化方法[J].地球物理学报,2013,56(3):834-841.

