一类解析函数的三阶Hankel行列式上界估计

张海燕,汤获,马丽娜

(赤峰学院数学与统计学院,内蒙古 赤峰 024000)

一类解析函数的三阶Hankel行列式上界估计

张海燕,汤获,马丽娜

(赤峰学院数学与统计学院,内蒙古 赤峰 024000)

主要研究了与对称点有关的一类解析函数Ms(α,µ,A,B)的三阶Hankel行列式H3(1),得到了该行列式的上界估计.

解析函数;对称点;三阶Hankel行列式;上界估计

1 引言

设S表示单位圆盘D={z∈C:|z|＜1}内单叶解析且具有如下形式的函数族

设P表示单位圆盘D={z∈C:|z|＜1}内具有如下形式且满足条件Rep(z)＞0的函数族

由文献[1]中的结论易知,对于函数p(z)∈P,存在Schwarz函数ω(z),使得

定义1.1[2]设函数f(z)和g(z)在单位圆盘D内解析.如果存在D内的Schwarz函数ω(z),满足:ω(0)=0,|ω(z)|＜1且f(z)=g(ω(z)),则称f(z)从属于g(z),记为f(z)≺g(z).特别地,如果g(z)在D内单叶,则

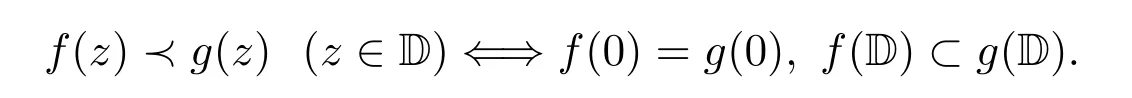
2013年,汤获,邓冠铁在文献[3]中引入与对称点有关的一类解析函数,并讨论了该函数类的系数估计.

定义 1.2[3]设Ms(α,µ,A,B)是具有(1.1)的形式且满足下面条件的函数全体,

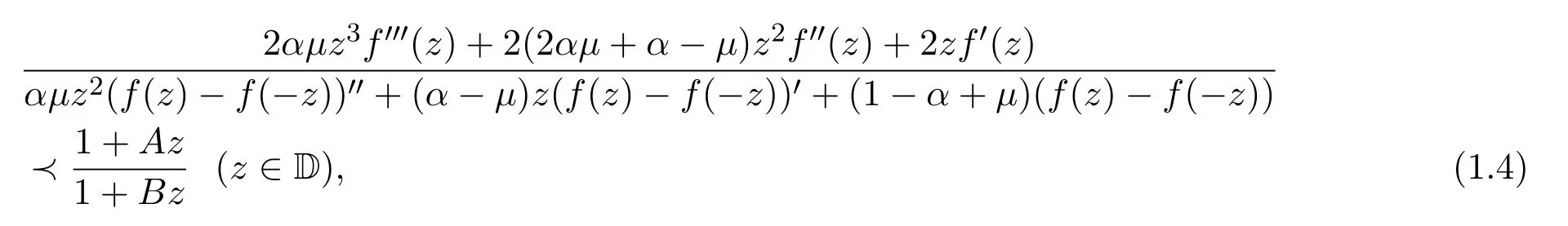
其中−1≤B＜A≤1,0≤µ≤α≤1.

由从属的定义可知f∈Ms(α,µ,A,B)当且仅当

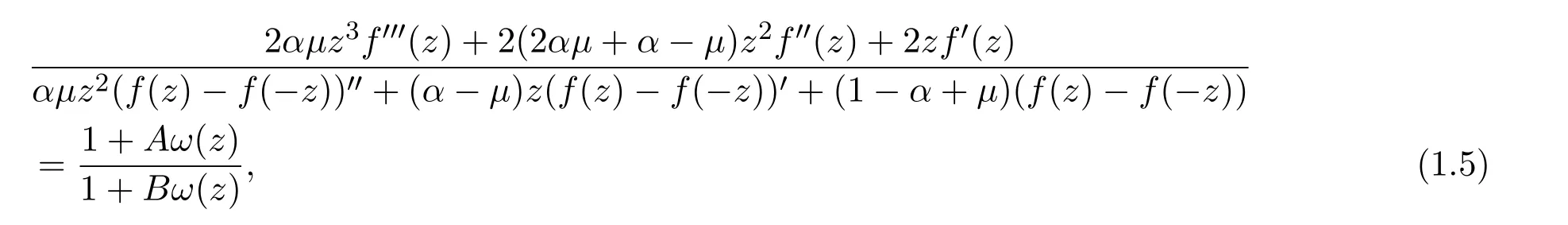
其中ω(z)是单叶解析函数,且满足ω(0)=0,|ω(z)|≤1,z∈D.

1976年,Noonan和Thomas[4]定义了函数f的q阶Hankel行列式：

其中a1=1,n≥1,q≥1.

特别地,有

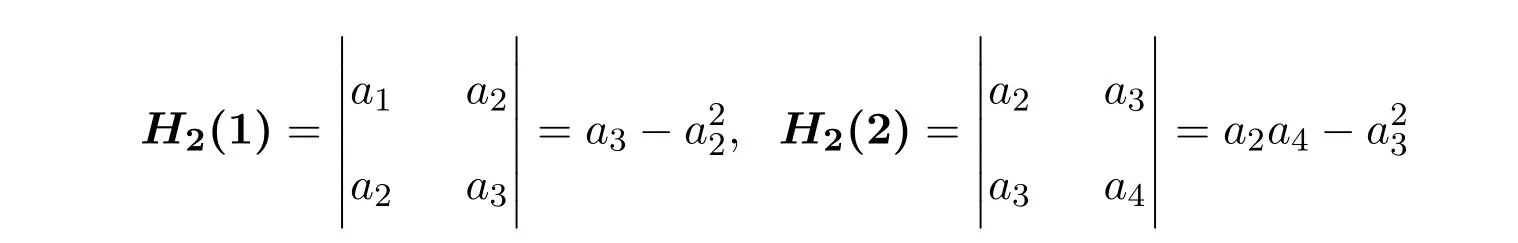
和

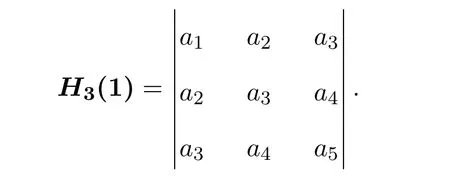
因为f∈S,a1=1,故有

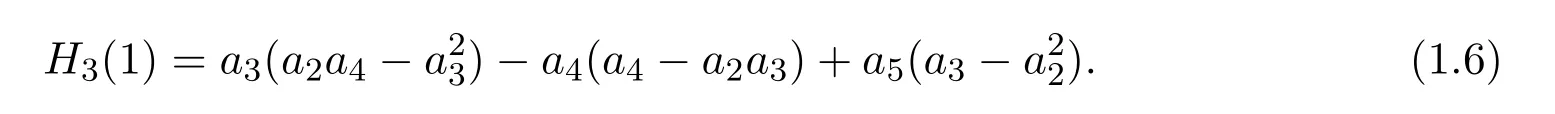
其中H2(1)的上界估计即是经典的Fekete-Szeg不等式[5].

近年来,越来越多的学者对Hankel行列式的研究产生了浓厚的兴趣.文献[4]研究了p叶函数的二阶Hankel行列式,文献[6]中研究了星象函数的行列式Hq(n),并确定了当n→∞时,行列式Hq(n)的增长率.文献[7]中研究了指数多项式的Hankel行列式,文献[8]中研究了积分序列的Hankel变换和一些性质.其他关于H2(2)的上界估计问题的研究,如文献[9-11].但到目前为止,对于三阶Hankel行列式H3(1)的研究较少(见文献[12][13]).受以上启发,研究与对称点有关的一类解析函数Ms(α,µ,A,B)的三阶Hankel行列式H3(1),给出了其上界估计.

2 主要结果

除非特别说明,在本文中,假设

为了证明本文结论,需要如下引理.

引理 2.1[2]如果p(z)∈P,则

引理 2.2[14]如果p(z)∈P,则存在复数x,z,满足|x|≤1,|z|≤1,使得

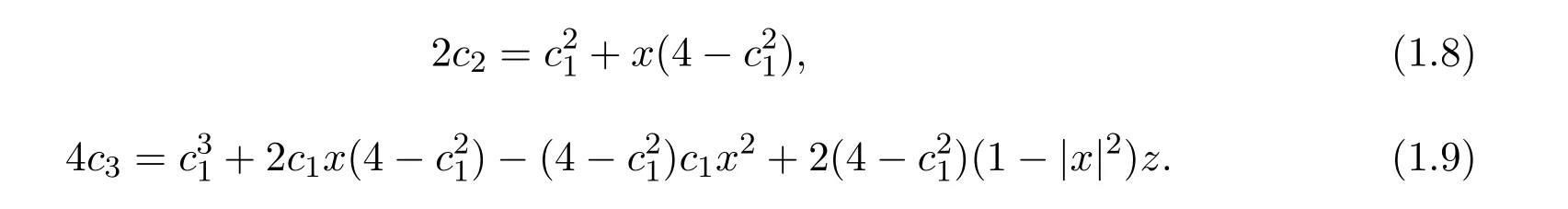
引理 2.3[3]设f∈Ms(α,µ,A,B),则

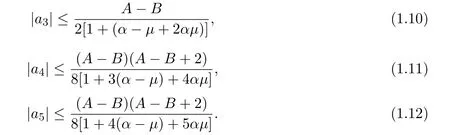
借助于上面引理及下面几个定理的结论,得到了函数Ms(α,µ,A,B)的三阶Hankel行列式的估计.

定理 2.1若f∈Ms(α,µ,A,B),则有

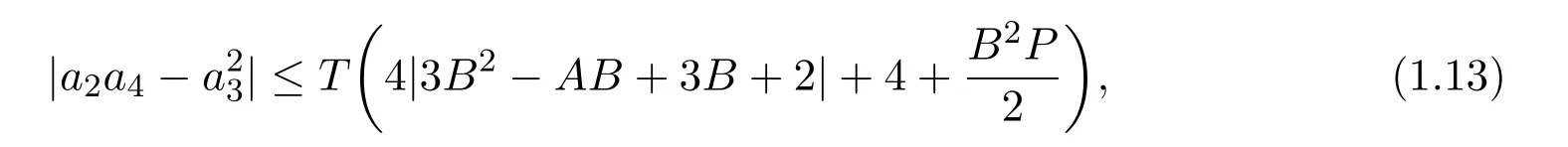
其中

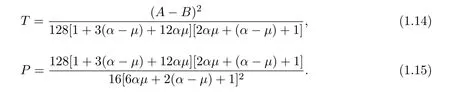
证明设f∈Ms(α,µ,A,B),由从属定义和(1.5)式可得

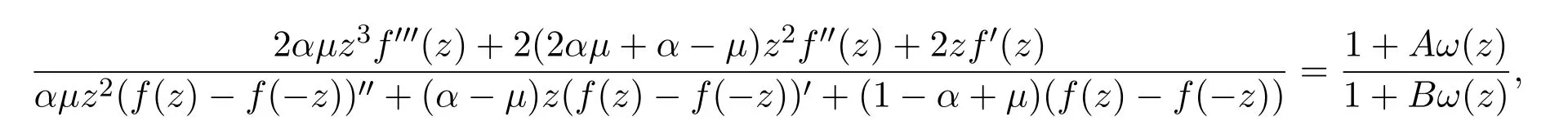
其中ω(z)是单叶解析函数,且满足ω(0)=0,|ω(z)|≤1,z∈D.设

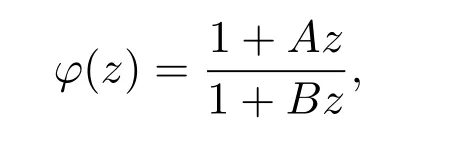
则

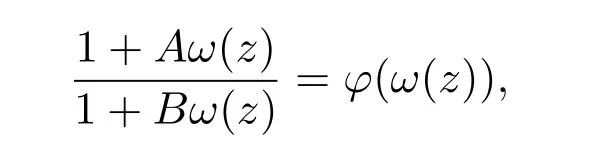
且

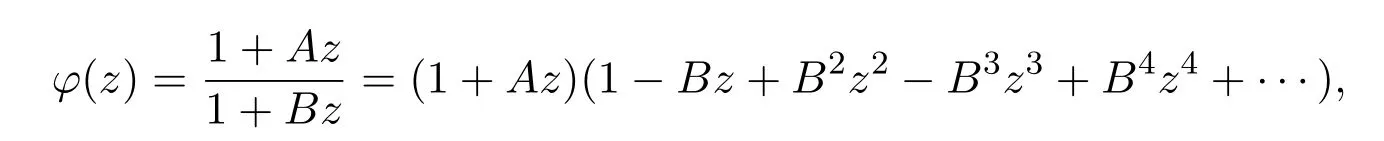
即

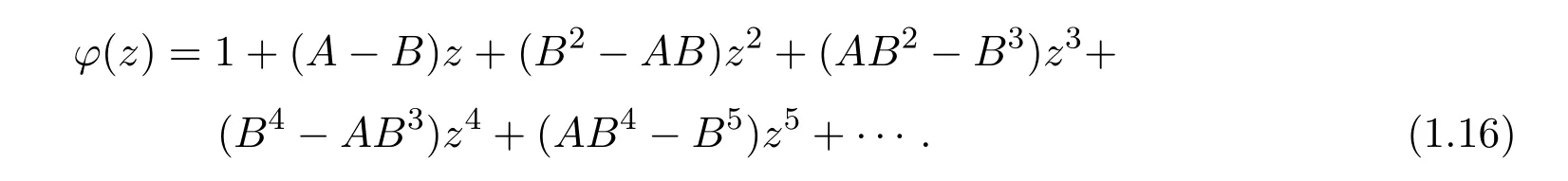
定义函数p(z)如下:

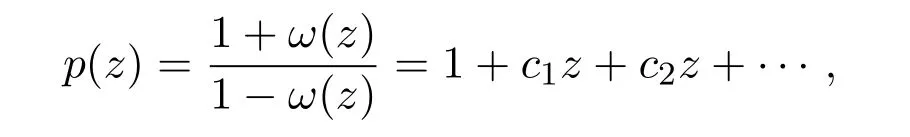
则p(z)∈P且

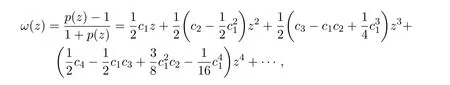
故有

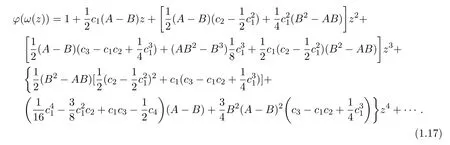
又

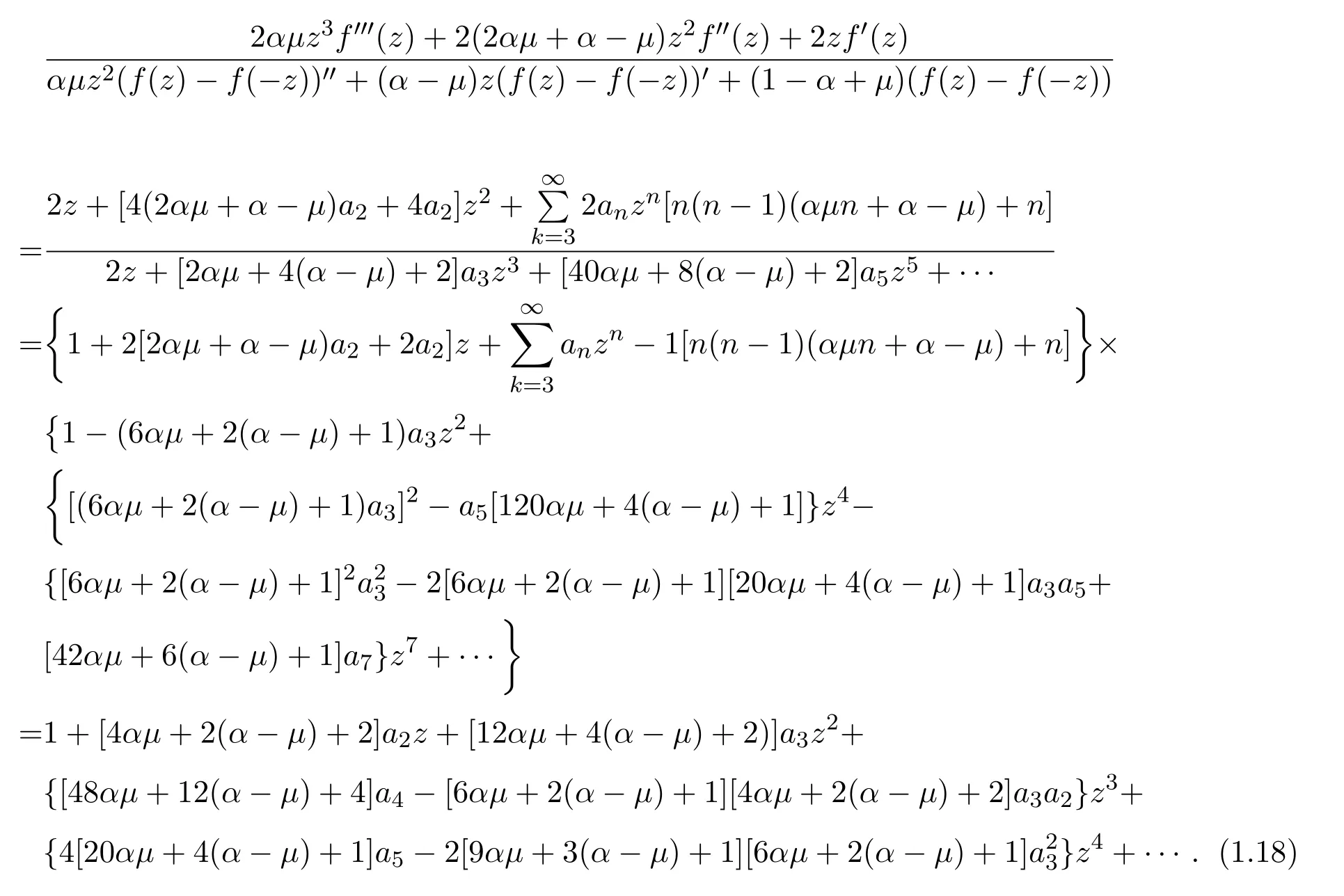
分别比较(1.17)式、(1.18)式中z,z2,z3的系数,得

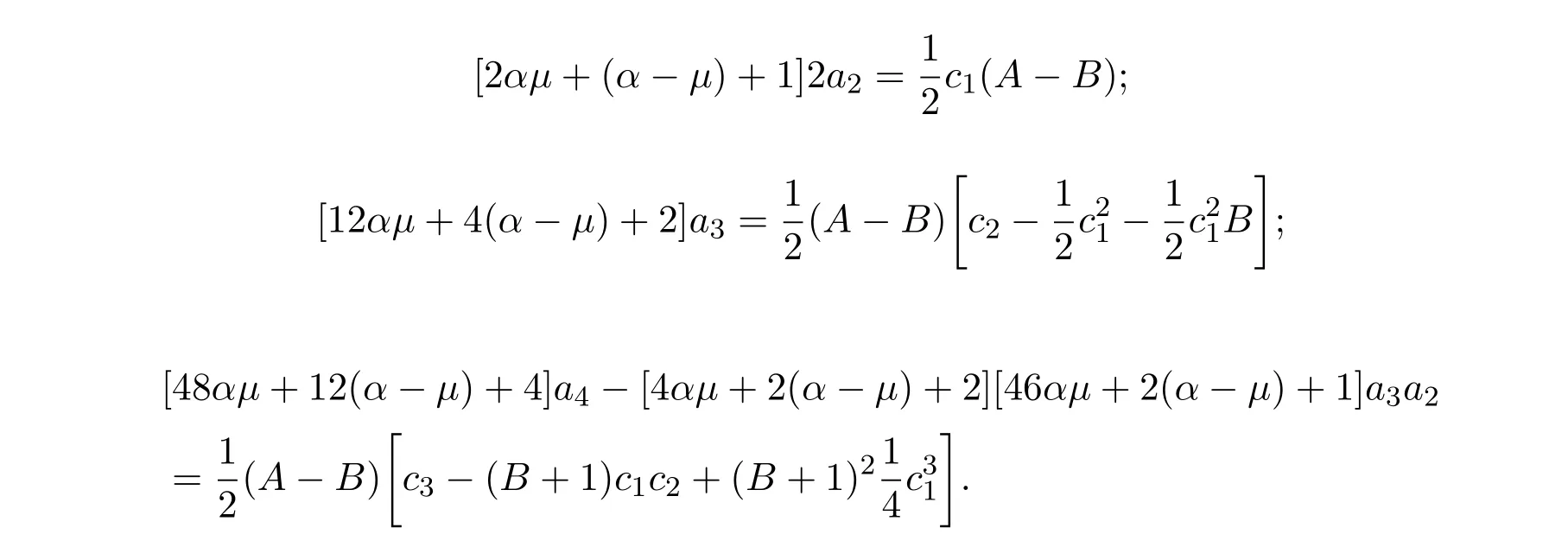
于是,有

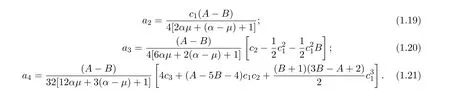
从而,有

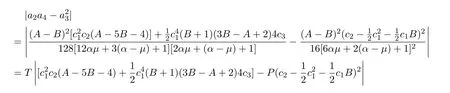
其中

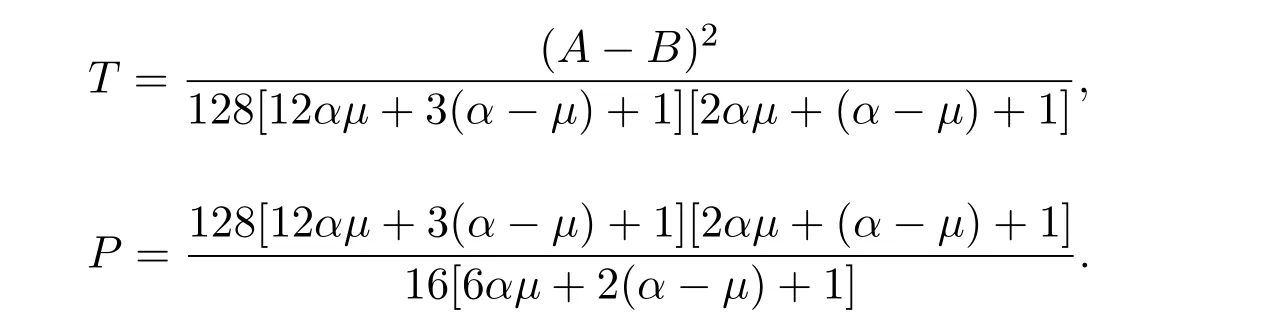
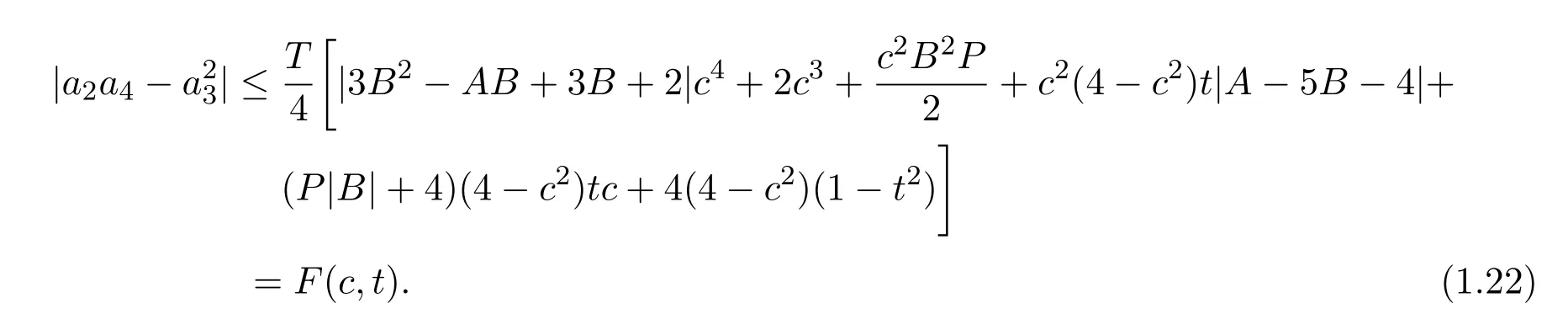
进而,有

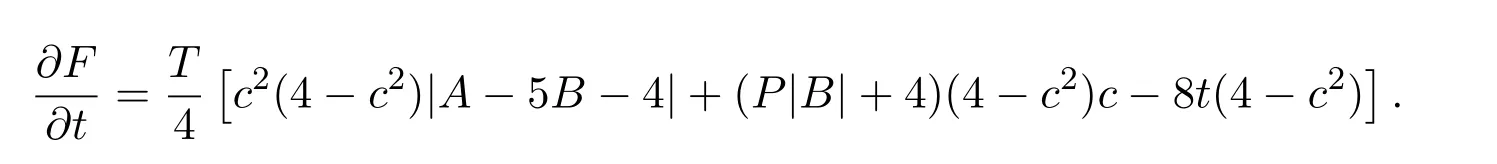
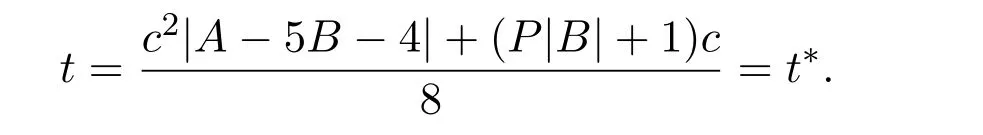
下面分两种情况进行讨论:

(1)当t＞t∗时,＜0,函数F(c,t)关于t严格单调递减,F(c,t)在t=0取最大值,即

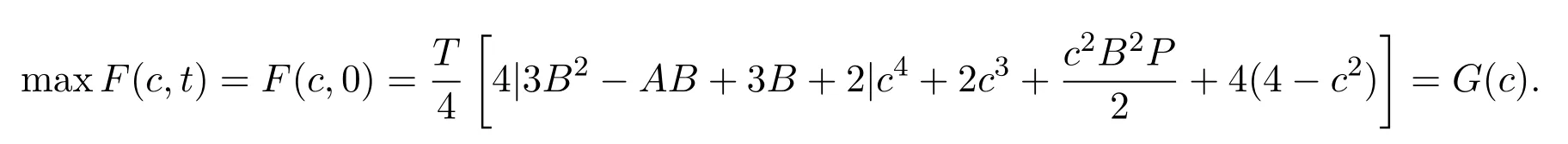
因为

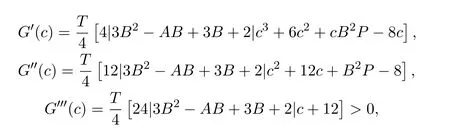
故函数G′(c)严格单调递增.由于c∈[0,2],因此G′(c)＞G′(0)=B2P−8.由于0≤P≤8,−1≤B≤1及c的任意性,可知G′(c)≥0,从而G′(c)单调递增.从而有G′(c)≥G′(0)=0,即函数 G(c)单调递增,因此函数 G(c)在 c=2处取到最大值.综上可知,函数 F(c,t)在t=0,c=2处取得最大值,即

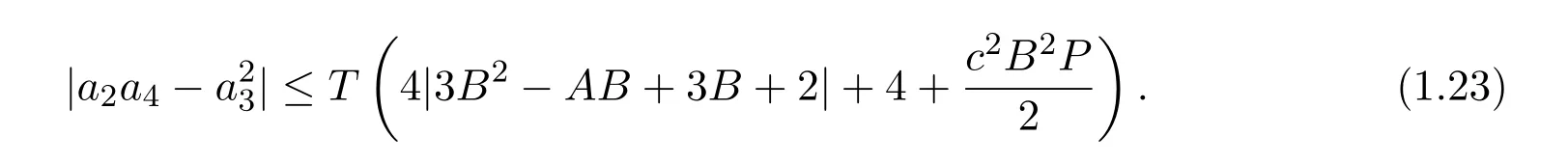
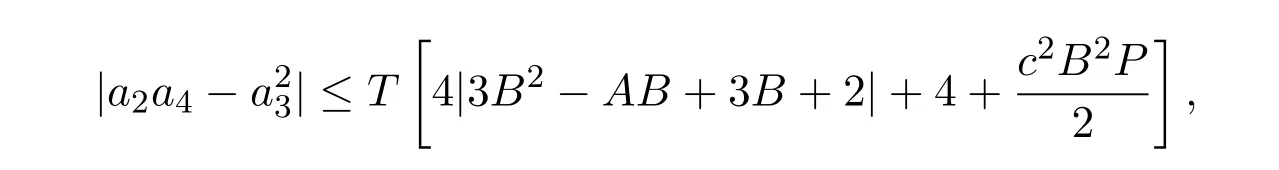
其中

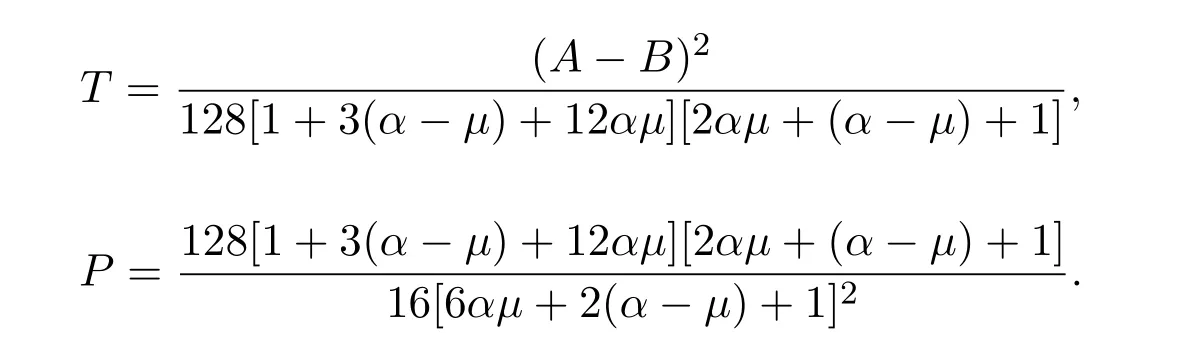
定理 2.2若f∈Ms(α,µ,A,B),则有

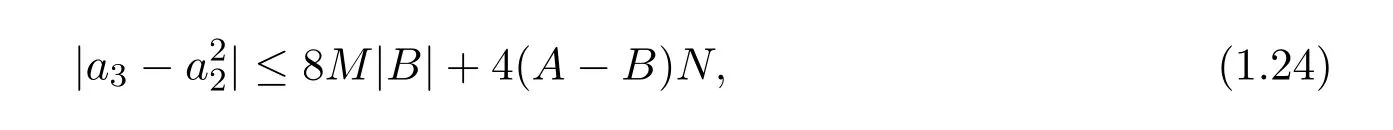
其中

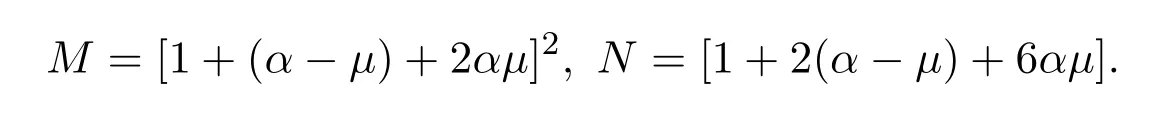
证明此定理的证明方法与定理2.1类似,在此省略其证明过程.

定理 2.3若f∈Ms(α,µ,A,B),则有

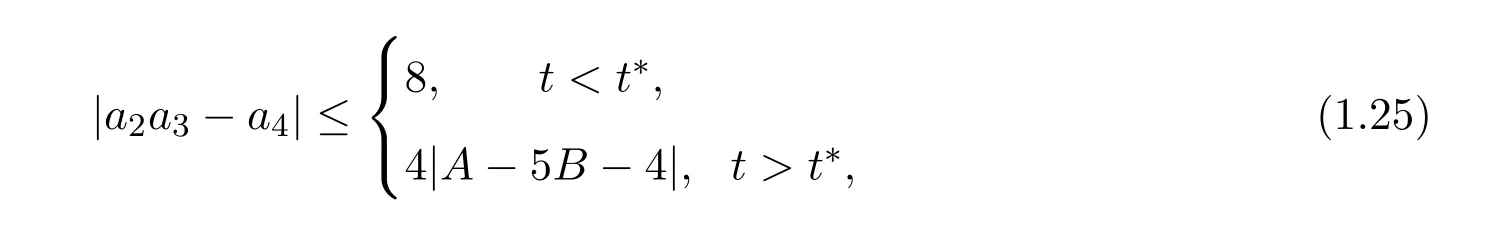
其中

证明由(1.19),(1.20),(1.21)式,可得

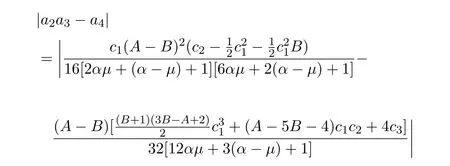
设|x|=t,0≤t≤1,c1=c,c∈[0,2],又因为|z|≤1,则由三角不等式和引理2.2,可得

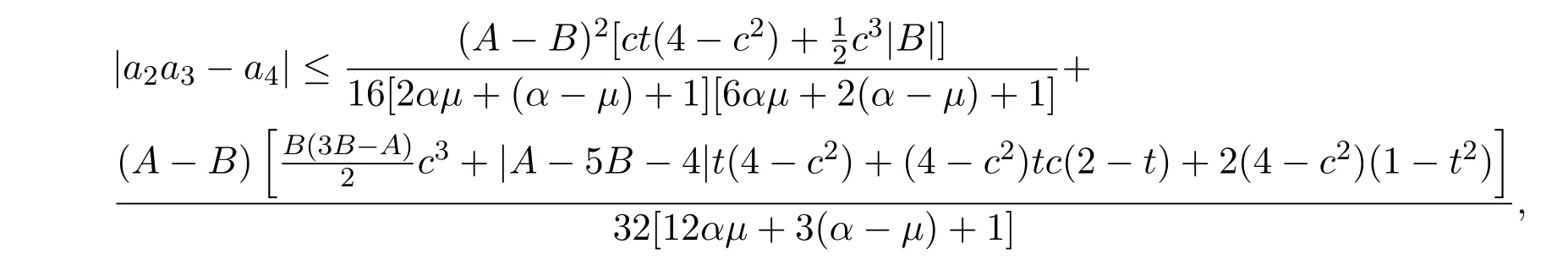
即

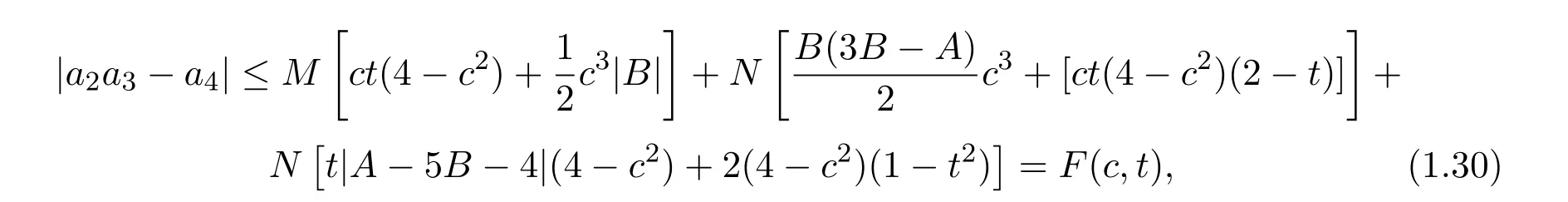
其中

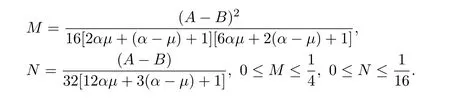
进而,有

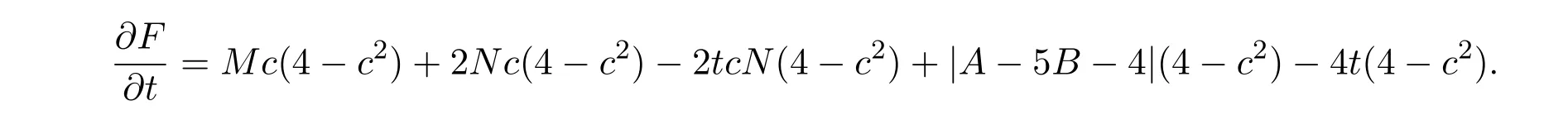
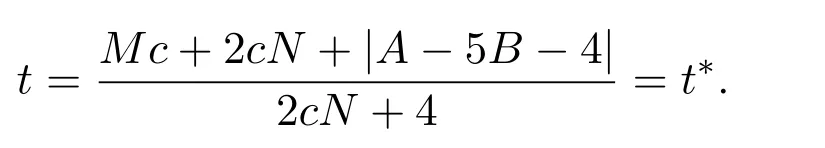
下面分两种情况进行讨论:

(1)当t＞t∗时,＜0,函数F(c,t)关于t严格单调递减,F(c,t)在t=0取最大值,即

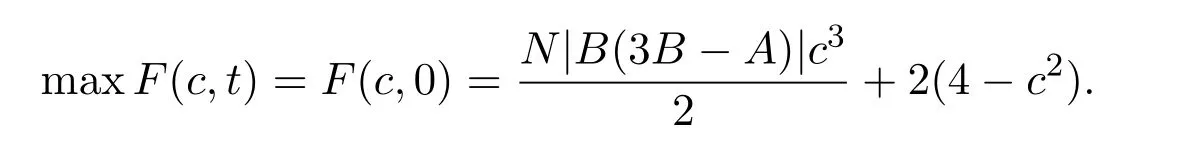
令

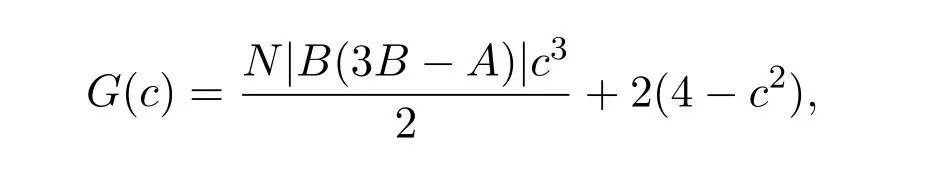
则由

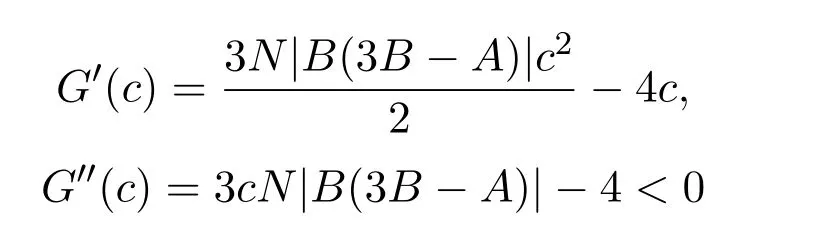
可得G′(c)严格单调递减.因为c∈[0,2],所以G′(c)≤G′(0)=0,进一步可得G(c)单调递减.因此函数G(c)在c=0取最大值.综上可知,函数F(c,t)在t=0,c=0处取得最大值,即

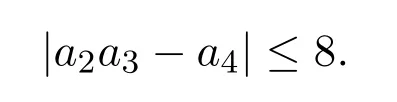
(2)类似地,当t＜t∗时,＞0,函数F(c,t)关于t严格单调递增,F(c,t)在t=1处取得最大值,G(c)在c=0处取得最大值.因此函数F(c,t)在t=1,c=0处取得最大值,即

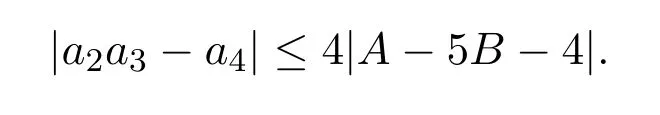
综上可知,定理2.3得证.

定理 2.4设f∈Ms(α,µ,A,B)则有

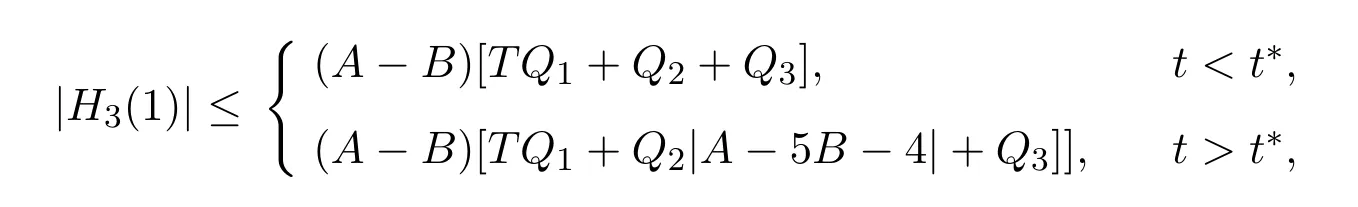
其中

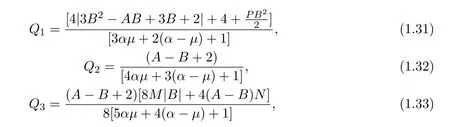
T,P M,N分别由(1.14),(1.15),(1.27),(1.28)式给出.

证明因为

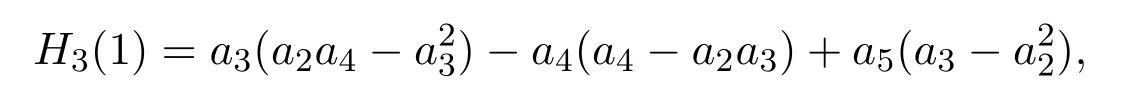
故由三角不等式可得

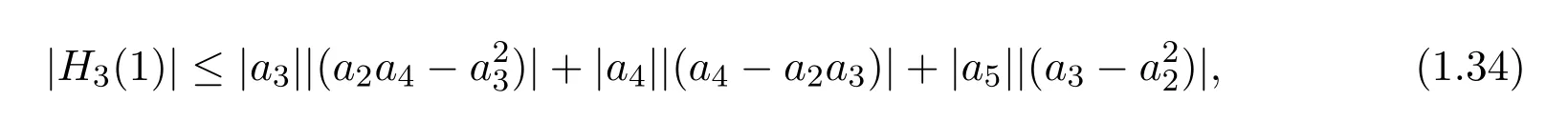
将(1.10),(1.11),(1.12),(1.13),(1.24),(1.25)式代入到(1.34)式,即得定理2.4的结论.

[1]Graham I,Kohr G.Geometric Function Theory in One and Higher Dimensions[M].New York:Marcel Dekker,2003.

[2]Duren P L.Univalent Functions[M].New York:Springer Verlag,1983.

[3]Tang Huo,Deng Guan tie.Coefficient estimates for new subclasses of analytic functions with respect to other points[J].Tamkang Journal of Mathematics,2013,2(44):141-148.

[4]Noonan J W,Thomas D K.On the second Hankel determinant of areally mean p-valent functions[J]. Transactions of the American Mathematical Society,1976,223(2):337-346.

[5]Fekete M,Szeg G.Eine benberkung uber ungerada schlichte funktionen[J].J.London Math.Soc.,1933,8:85-89.

[6]Noor K I.Hankel determinant problem for the class of functions with bounded boundary rotation[J].Rev. Roumaine Math.Pures Appl.,1983,28(8):731-739.

[7]Ehrenborg R.The Hankel determinant of exponential polynomials[J].Amer.Math.Monthly,2000, 107(6):557-60.

[8]Layman J W.The Hankel transform and some of its properties[J].J.Integer Seq.,2001,4(1):1-11.

[9]Bansal D.Upper bound of second Hankel determinant for a new class of analytic functions[J].Appl.Math. Lett.,2013,26(1):103-107.

[10]Liu Mingsheng,Xu Junfeng,Yang Ming.Upper bound of second Hankel determinant for certain subclasses of analytic functions[J].Abstract and Applied Analysis,2014(1):1-10.

[11]Singh G.Hankel determinant for new subclasses of analytic functions with respect to symmetric points[J]. Int.J.of Modern Mathematical Sciences,2013,5(2):67-76.

[12]Raza M,Malik S N.Upper bound of the third Hankel determinant for a class of analytic functions related with lemniscate of bernoulli[J].Journal of Inequalities and Applications,2013,2013(1):412.

[13]Sudharsan T V,Vijayalakshmi S P,Adolf Stephen B.Third Hankel determinant for a subclass of analytic univalent functions[J].Malaya J.Mat.,2014,2(4):438-444.

[14]Libera R J,Zlotkiewicz E J.Coefficients bounds for the inverse of a function with derivative in positive coefficients[J].Proc.Amer.Math.Soc.,1983,87:251-257.

The estimate of upper bound of third Hankel determinant for a class of analytic functions

Zhang Haiyan,Tang Huo,Ma Lina
(School of Mathematics and Statistics,Chifeng University,Inner Mongolia 024000,China)

In this paper,we investigate the Hankel determinant H3(1)for a class of analytic functions with respect to symmetric points,denoted by Ms(α,µ,A,B),and obtain the estimate of upper bound of the above determinant.

analytic functions,symmetric points,third Hankel determinant,upper bound

30C45,30C50

A

1008-5513(2017)02-0211-10

10.3969/j.issn.1008-5513.2017.02.013

2016-11-04.

国家自然科学基金(11561001);内蒙古自治区高等学校科学研究项目(NJZY16251).

张海燕(1982-),硕士,讲师,研究方向：算子代数与复分析.

2010 MSC:30C45,30C55