一类新型Szasz-Kantorovich-Bezier算子在Orlicz空间内的逼近

孙芳美,吴嘎日迪

(内蒙古师范大学数学科学学院,内蒙古 呼和浩特 010022)

一类新型Szasz-Kantorovich-Bezier算子在Orlicz空间内的逼近

孙芳美,吴嘎日迪

(内蒙古师范大学数学科学学院,内蒙古 呼和浩特 010022)

研究了一类新型Szasz-Kantorovich-Bezier算子在Orlicz空间内的逼近问题.在连续函数空间和Lp空间内研究算子逼近方法的基础上,利用函数逼近论中的常用方法和技巧以及K泛函、Ditzian-Totik模、Holder不等式、Cauchy不等式、凸函数的Jensen不等式等工具得到了该算子在Orlicz空间内的逼近正定理、逆定理和等价定理.由于Orlicz空间包含连续函数空间和Lp空间,其拓扑结构也比Lp空间复杂得多,所以本文的结果具有一定的拓展意义.

新型Szasz-Kantorovich-Bezier算子;Orlicz空间;正定理;逆定理;等价定理

1 定理及主要结果

近年有一类称为Bezier型算子在Lp空间及Orlicz空间内得到了一系列的研究.2006年郭顺生在文献[1]中引入并讨论了Szasz-Kantorovich-Bezier算子

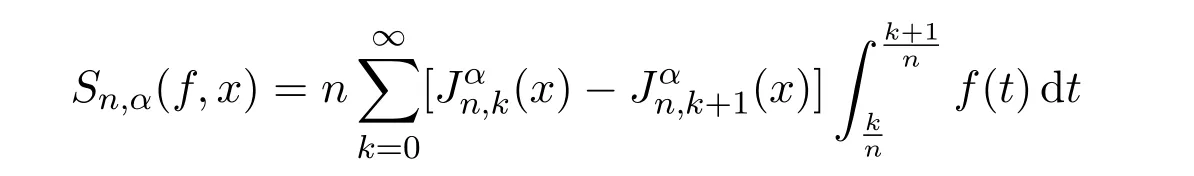
在Lp空间内的逼近问题，其中是Bezier基函数,

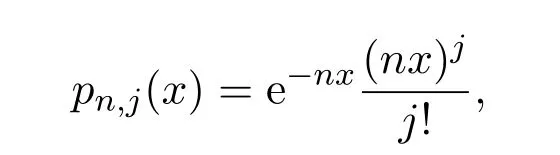
且以Ditzian-Totik模为工具得到了该算子在Lp空间内的逼近正定理、逆定理和等价定理.在文献[2]中定义了一类新型Szasz-Kantorovich-Bezier算子

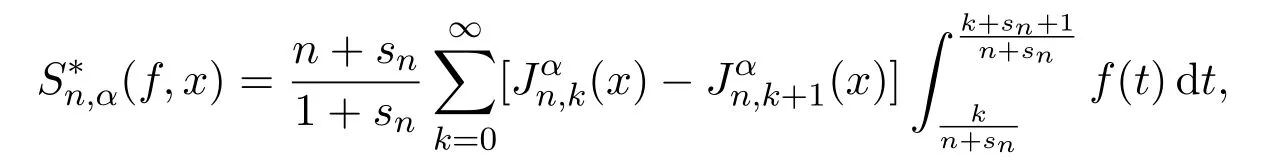
其中{sn}为一有界的正数列,并研究了该算子在Lp空间内的逼近正定理、逆定理和等价定理.当sn=0时,即为通常的Szasz-Kantorovich-Bezier算子.至今为止尚未看到这类新型Szasz-Kantorovich-Bezier算子在Orlicz空间内的逼近性质.为此,本文在Orlicz空间内研究了该算子的逼近性质,并得到了该算子在Orlicz空间内的逼近正定理、逆定理和等价定理.

文中用M(u)和N(v)表示互余的N函数,关于N函数的定义及其性质见文献[3].由N函数M(u)生成的Orlicz空间是指具有有限的Orlicz范数

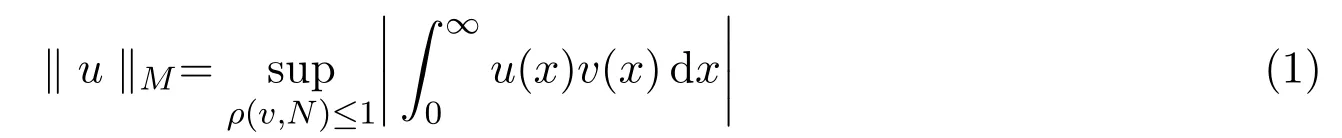
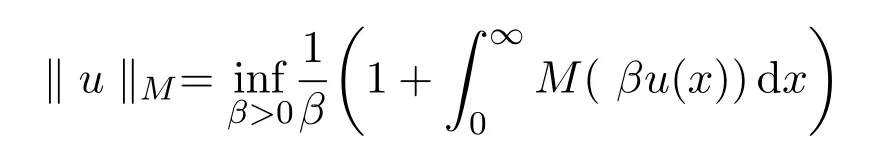
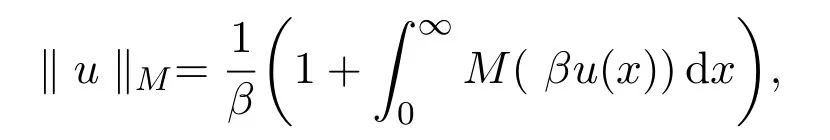
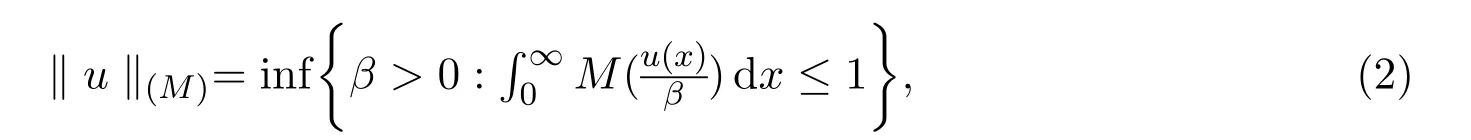
定理1.1设则

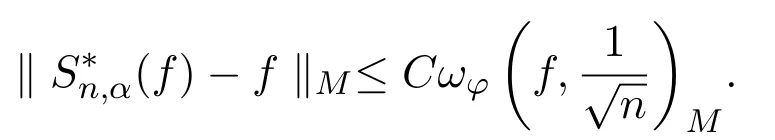
定理1.2设则

定理1.3设则

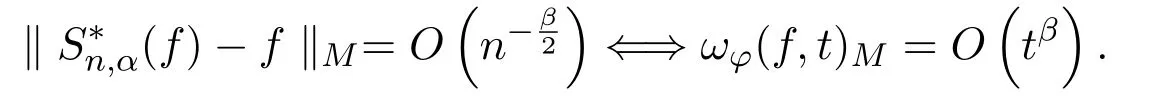
注1.1由Orlicz范数(1)和Luxemburg范数(2)的等价性容易看出,正定理和逆定理的结论在Orlicz空间内同样成立.本文中用C表示绝对正常数,并且在不同处可以表示不同的值.

2 相关引理

连续模和K泛函定义如下:

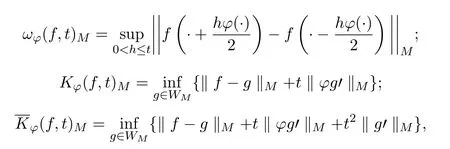
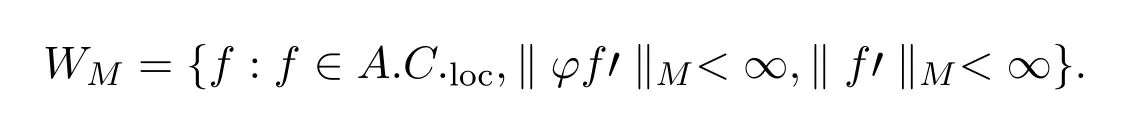
则根据文献[1,4,5]容易推得

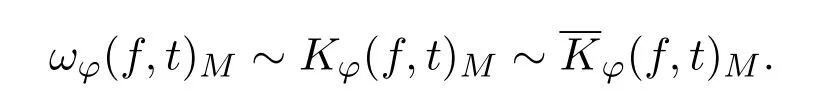
引理2.1[1]1=Jn,0(x)＞Jn,1(x)＞···＞Jn,k(x)＞Jn,k+1(x)＞···＞0,x∈[0,∞).

引理2.2[1]p′n,k(x)=n(pn,k−1(x)−pn,k(x)),k=1,2,···,p′n,0(x)=−npn,0(x).

引理2.3[1]J′n,0(x)=0,J′n,k(x)=npn,k−1(x)＞0,k=1,2,···.

引理2.4[1]

引理2.5当x∈[0,∞)时,其中

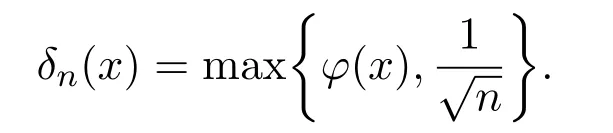
证明经过简单的计算可以得到

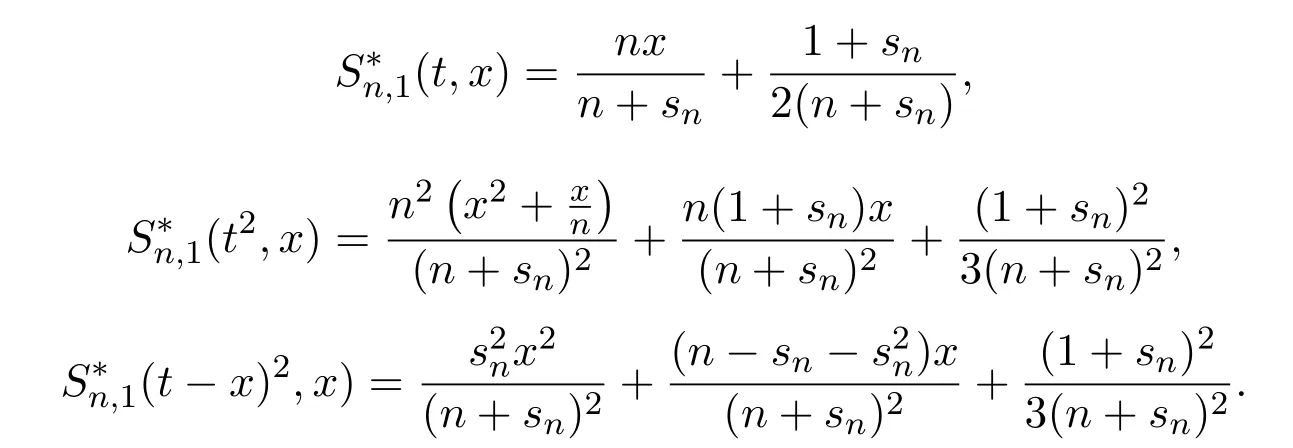
因为{sn}是有界量,则

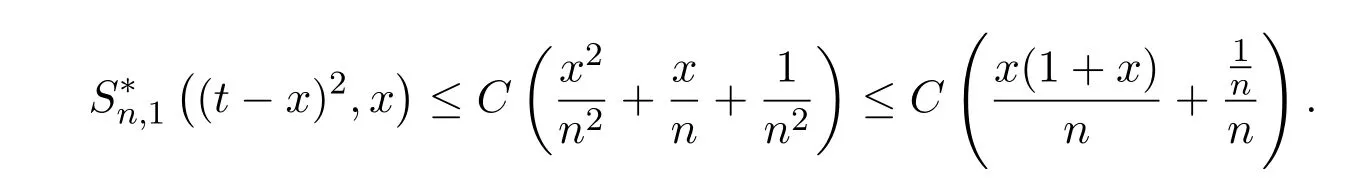
所以

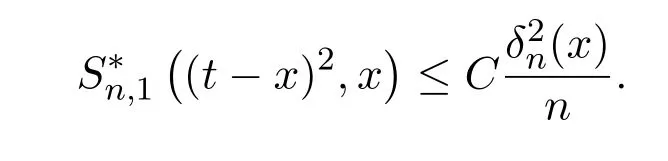
引理2.6[1]由于 α≥1时,aα−bα≤α(a−b),0≤b≤a≤1,则

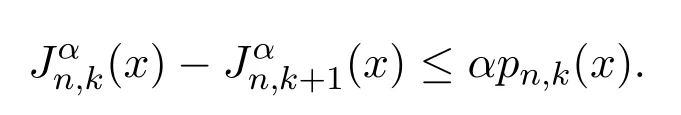
引理2.7是从的有界线性算子,且

证明的线性性是显然的.下证有界性

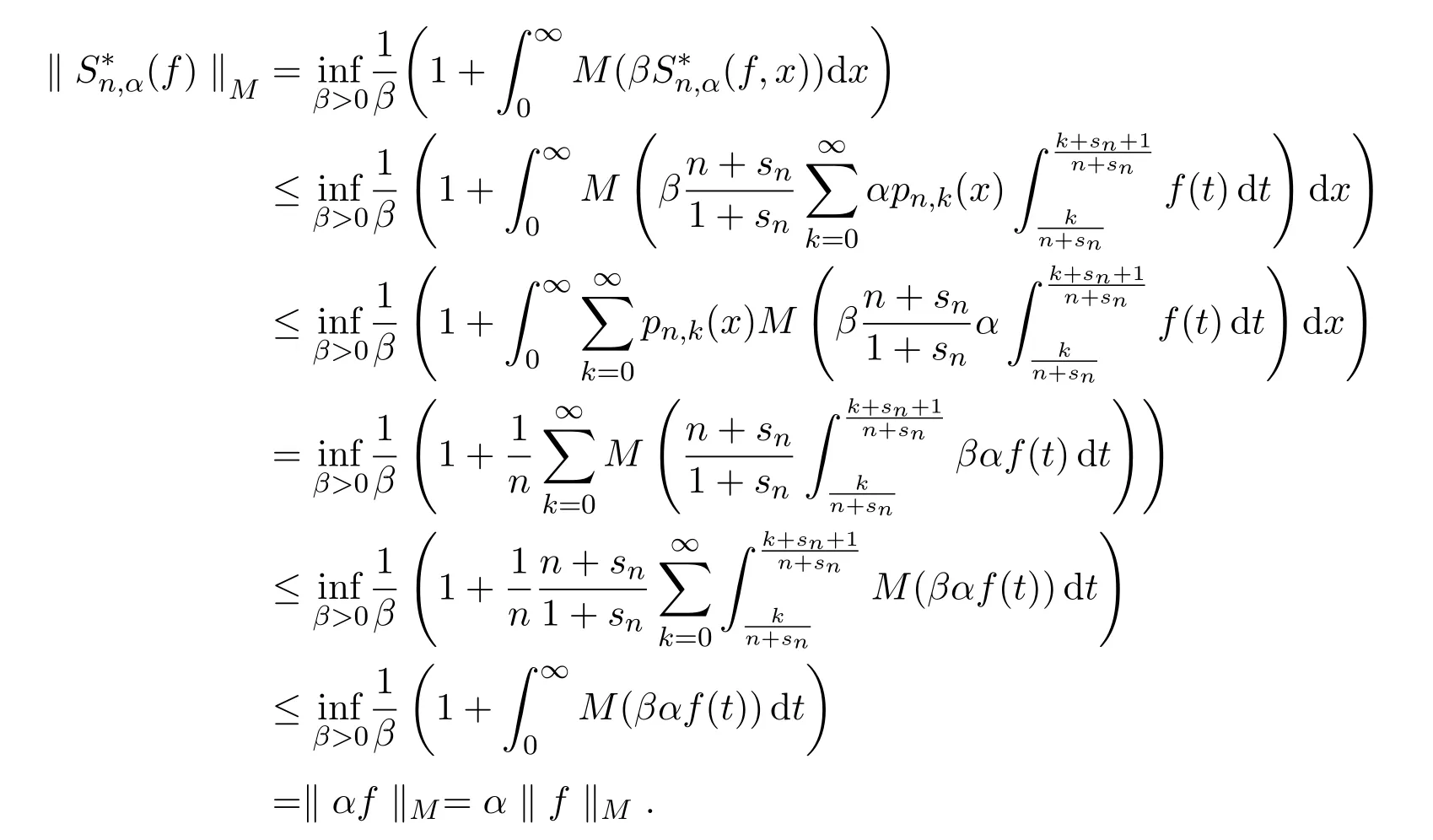
引理2.8对于有

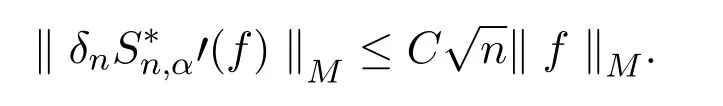
证明通过简单的计算有

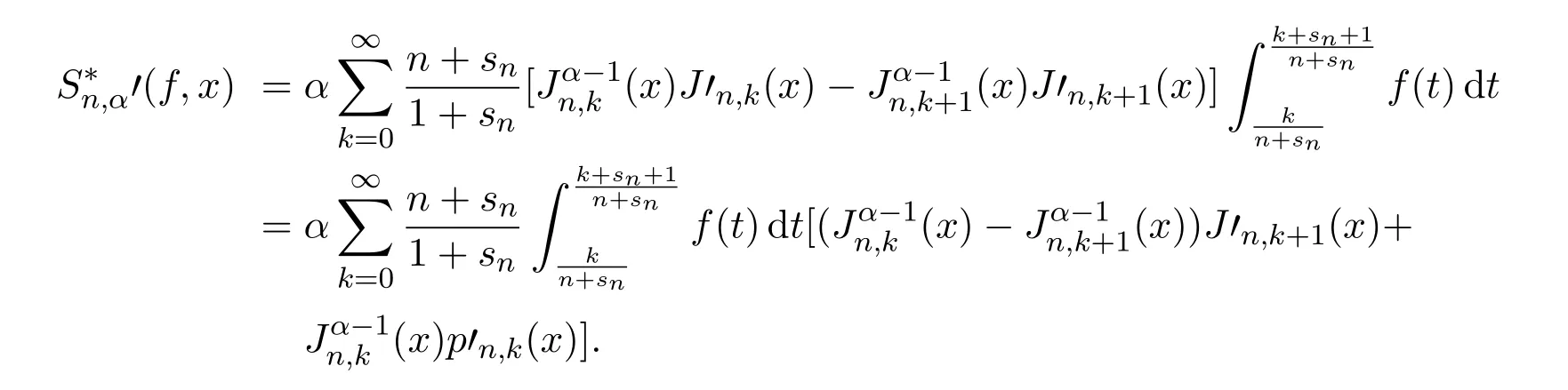
类似文献[6]中由Orlicz空间内的Holder不等式推出的结论容易推得

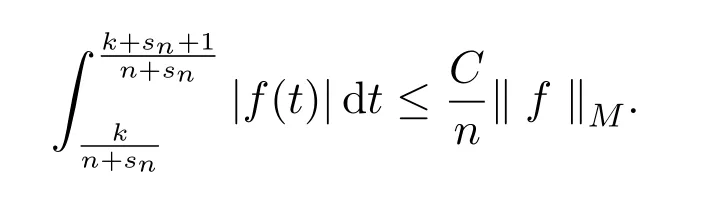
故有

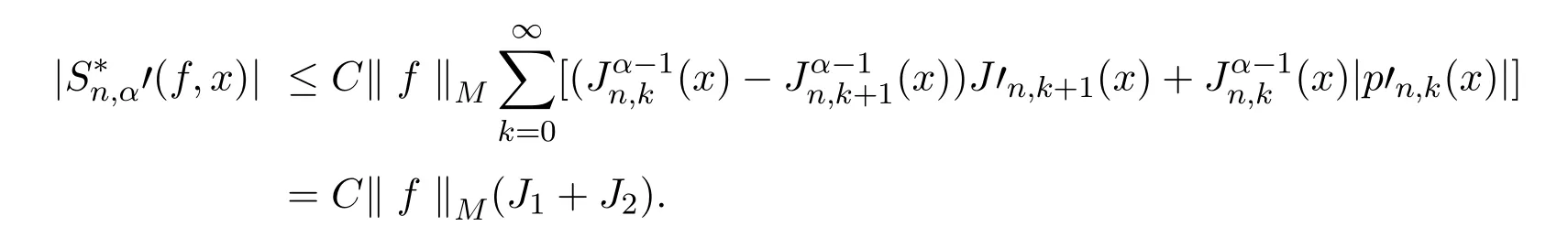
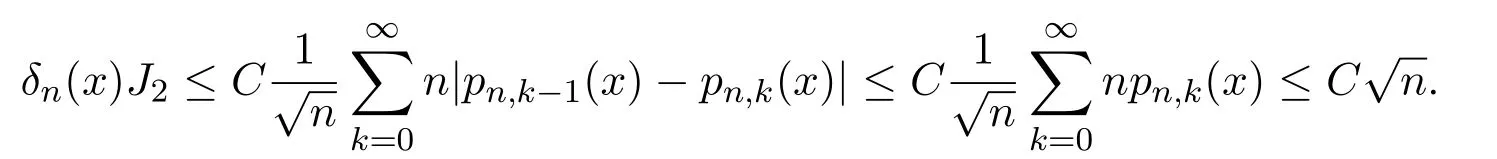
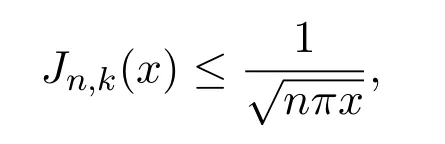
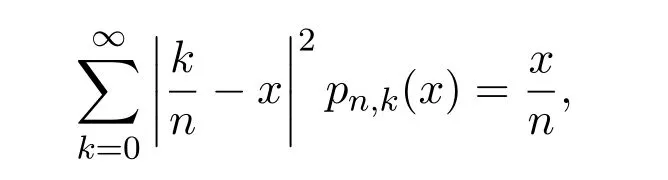
结合引理2.4可得

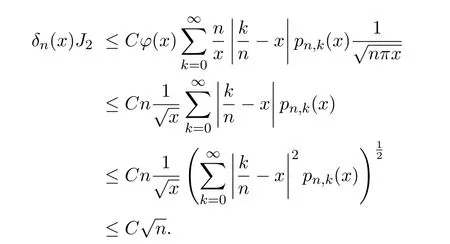
于是可得

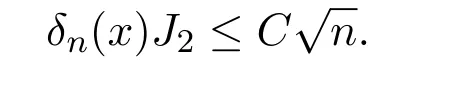
注意到J′n,0(x)=0,则

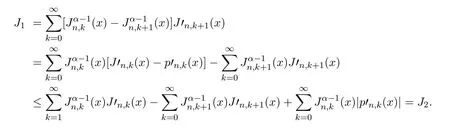
因此知

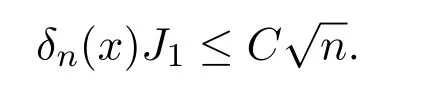
综上

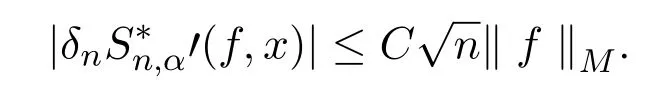
故而

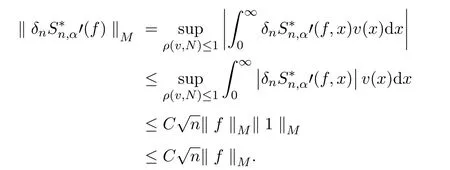
引理2.9对于有

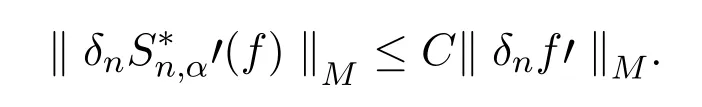
证明由于=0,有

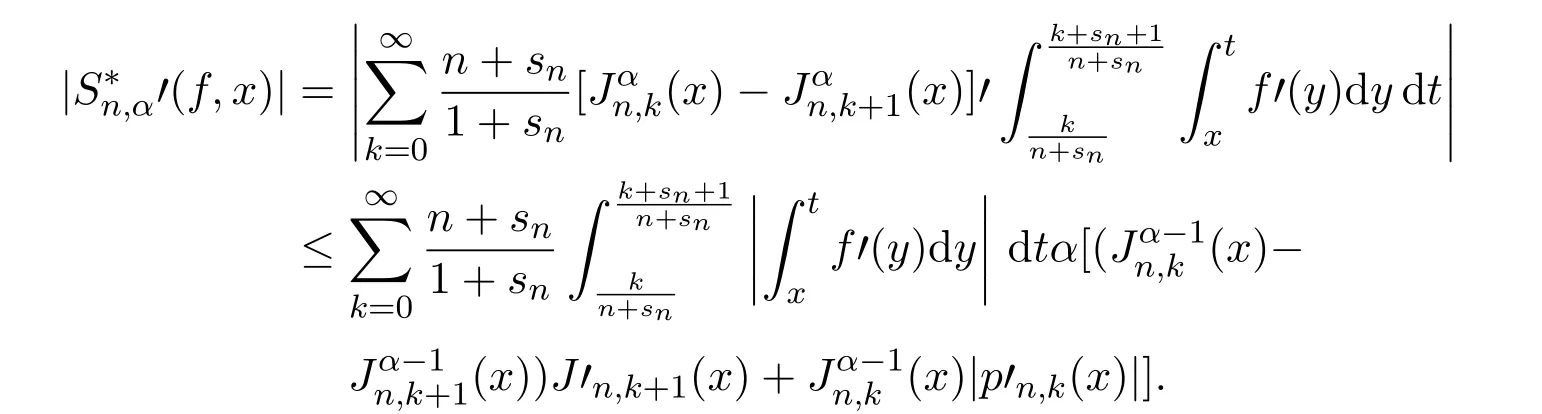
又

且

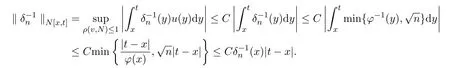
因而

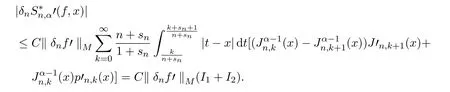
由文献[2]中引理2.7的证明直接可得

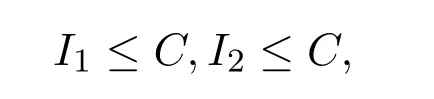
所以

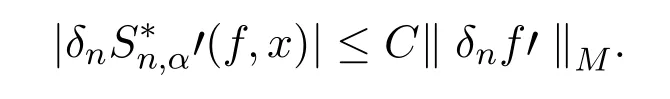
从而

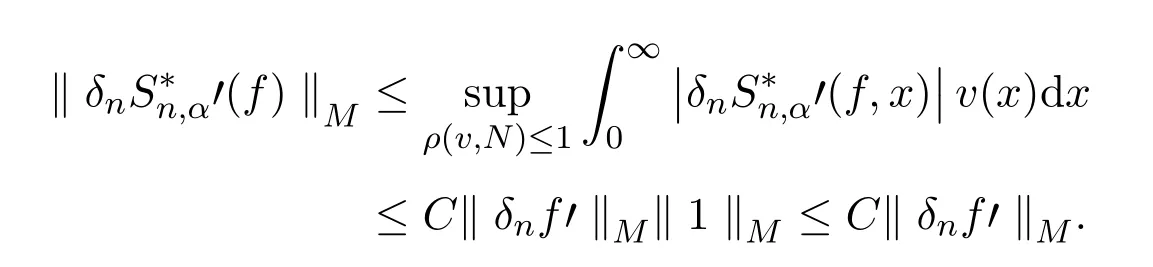
3 定理的证明

定理1.1的证明利用K泛函与连续模的等价关系式知,存在g∈WM,使得

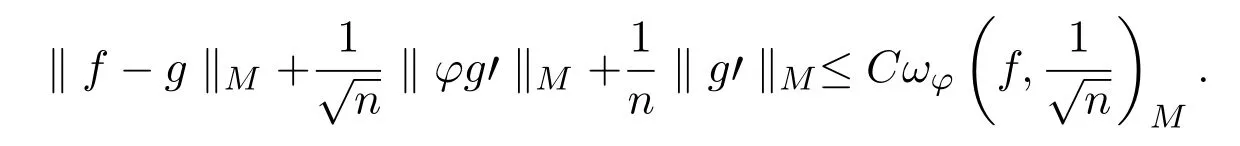
结合引理2.7有

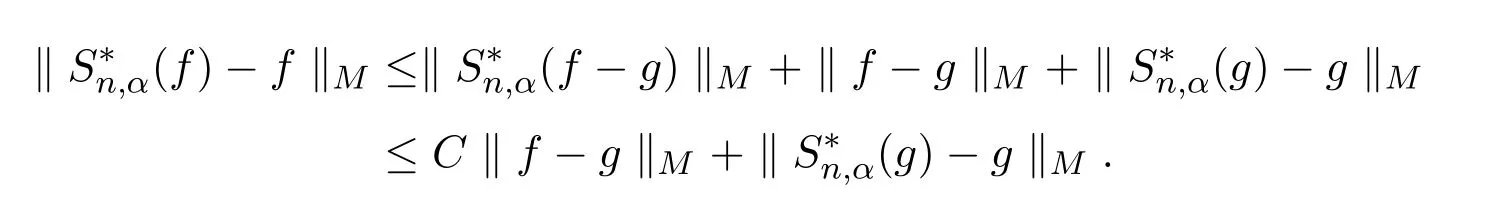
因此只需证明

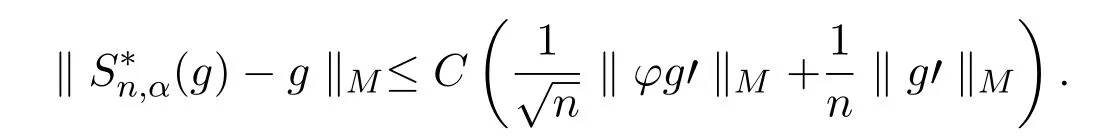
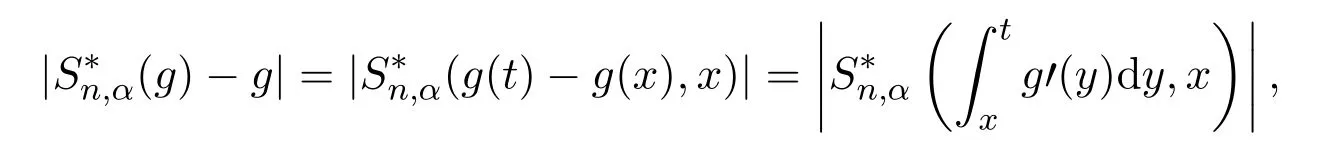
又

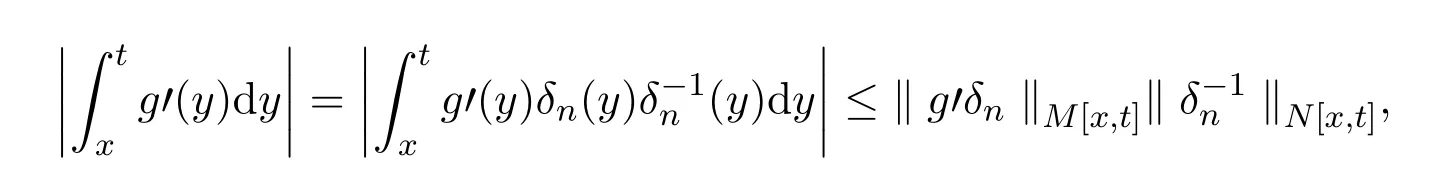
由引理2.9证明过程,有

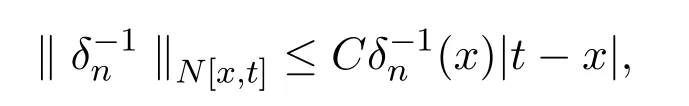
故

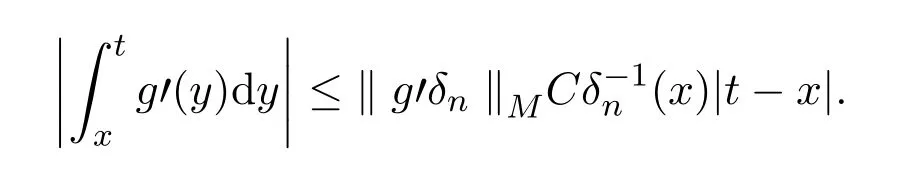
从而,有

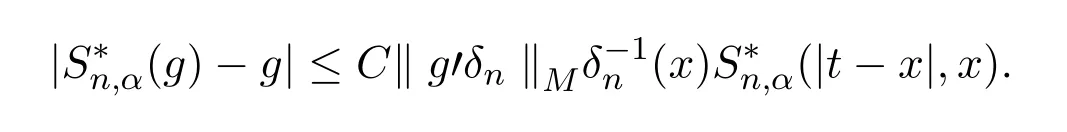
综合利用Cauchy不等式,凸函数的Jensen不等式,可得

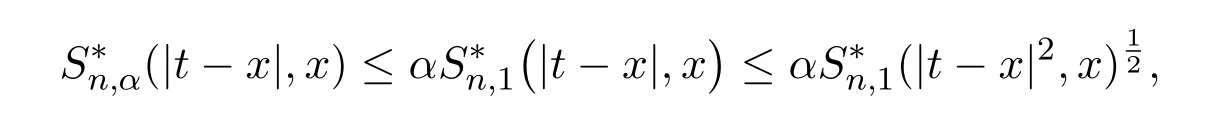
由引理2.5可得

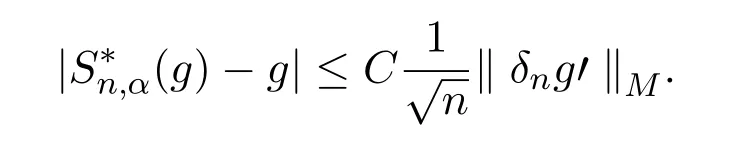
故

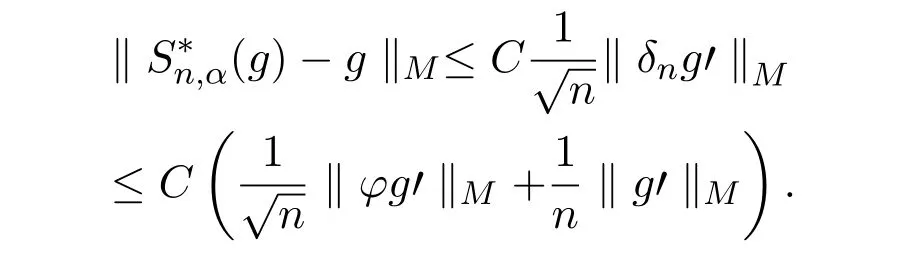
综上即可证得定理1.1.

定理1.2的证明由引理2.8,引理2.9及K泛函与连续模的等价关系知,存在g∈WM,有

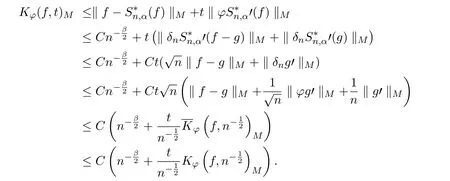
利用文献[5]中Berens-Lorentz引理可得

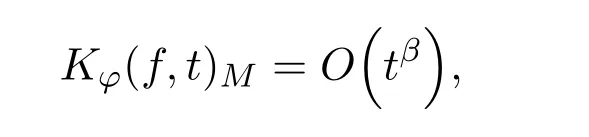
又由

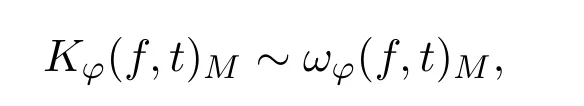
有

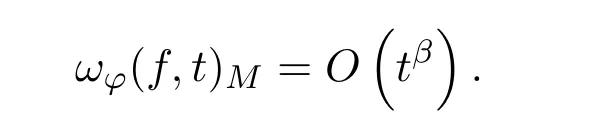
定理1.3的证明 ”⇒”见定理1.2.

”⇐” 由于

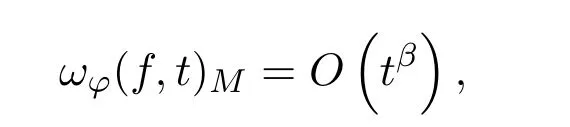
所以充分性由由根定理1.1可以直接得到.

参考文献

[1]郭顺生,齐秋兰,李清.Szasz-Kantorovich-Bezier算子在 Lp[0,∞)上的逼近定理 [J].数学研究与评论, 2006,26(4):744-755.

[2]卢敏.一类新型Szasz-Kantorovich-Bezier算子逼近[D].宁夏大学:图书馆,2009.

[3]吴从炘,王廷辅.奥尔里奇空间及其应用[M].哈尔滨:黑龙江科学技术出版社,1983.

[4]Wu Garidi.On approximation by polynomials in Orlicz spaces[J].Approximation Theory and its Applications,1991,7(3):97-110.

[5]Ditzian Z,TOotik V.Moduli of Smoothness[M].Berlin:Springer-Verlag,1987.

[6]冯悦,吴嘎日迪.Shepard算子在Orlicz空间内的逼近等价定理[J].内蒙古师范大学学报,2010,39(6):566-567.

[7]Zeng Xiaoming.On the rate of convergence of the generalized Szasz type operators for bounded variation functions[J].J.Math.Anal.Appl.,1998,226:309-325.

[8]邓雪莉,吴嘎日迪.关于Bernstein-Durrmeyer-Bezier算子在Orlicz空间内的逼近[J].纯粹数学与应用数学, 2015,31(3):307-317.

On approximation of a new type of Szasz-Kantorovich-Bezier operator in Orlicz spaces

Sun Fangmei,Wu Garidi
(College of Mathematics Science,Inner Mongolia Normal University,Huhhot 010022,China)

In this paper we investigate the approximation problem of a new type of Szasz-Kantorovich-Bezier operator in Orlicz spaces based on the methods of studying the operator approximation in continuous function space and Lpspace,and used common measures and techniques in function approximation theory.K-functional, modulus of Ditzian-Totik,Holder inequality,Cauchy inequality,the convex property of N-function,Jensen inequality are used as tools to obtain direct throrem,converse throrem and equivalence theorem in orlicz spaces. Because the Orlicz space includes continuous function space and Lpspace,and its topological structure is more complicated than Lpspace,the results of this paper have certain expansion significance.

Szasz-Kantorovich-Bezier operator,Orlicz space,direct throrem,converse throrem, equivalence theorem

O 174.41

A

1008-5513(2017)02-0168-09

10.3969/j.issn.1008-5513.2017.02.008

2016-12-08.

国家自然科学基金(11161033);内蒙古自治区研究生科研创新资助项目(S20161013501).

孙芳美(1994-),硕士生,研究方向：函数逼近论.

吴嘎日迪(1962-),硕士,教授,研究方向：函数逼近论.

2010 MSC:41A35