E-凸规划最优性问题研究

王世磊

（信阳学院 数学与信息学院，河南 信阳 464000）

E-凸规划最优性问题研究

王世磊

（信阳学院 数学与信息学院，河南 信阳 464000）

文章首先给出文献[1]中定理4.1的一个反例，并在对该文献的定理4.2进行修正的基础上给出了E-凸规划问题最优解的刻画；其次，给出一个E-凸规划问题的最优性充分条件；最后，在E-可微情形下得到E-凸规划问题最优解的相关结论.

E-凸函数；E-凸规划；E-可微；最优解；最优性条件

自从1999年Youness E A在文献[1]中首次提出E-凸规划问题的概念，并在2001年给出了E-凸规划的最优性准则以后[2]，许多学者开始对E-凸规划问题进行进一步的研究.Yang X M[3]和Chen X S[4]分别在2001和2002年指出Youness E A的E-凸规划的最优性条件的一些不正确结论并给出反例，简金宝[5]在2003年也给出Youness E A有关E-凸规划结论的反例.这些研究对相关结论所做的修正推进了E-凸和广义E-凸规划理论的发展：2003年，Youness E A拓展了自己对E-凸规划的研究，给出了多目标E-凸规划有效解的特征[6]； 2006年，覃义、简金宝把Youness E A的E-凸规划问题的概念转换成了新的等价规化问题并得到了相关结论[7]；2008年，Youness E A和Eman T[8]给出了在半-强-E函数下多目标规划问题中的表达公式，并给出求解这类优化问题有效解的方法（加权法（Weighting）和ε-约束方法（ε-constraint）），同时给出这类问题有可行解的充分必要条件；2011年，Megahed A A和Youness E A等人在充分研究Narula S C等提出的Refence direction方法，Wierzbicki L提出的Refence point方法，Steuer提出的Tchebycheff方法，Nakayama提出的Trade-off方法以及Wang X M等提出的ARP方法的基础上研究出了一种解决E-凸多目标非线性规划的新方法——结合的交互式方法[9]，并给出大量的实例展示了这种新方法的优点和高效性；2013年，Megahed A A[10]等人研究了当E-凸规划中f为E-可微情形时的优化条件.关于E-凸规划最优性理论的研究还在继续，还有很多值得深入探究的方面.

1 E-凸规划问题的描述

令E∶Rn→Rn是一映射，C为关于映射E的E-凸集，下面首先给出E-凸规划问题具体描述公式：

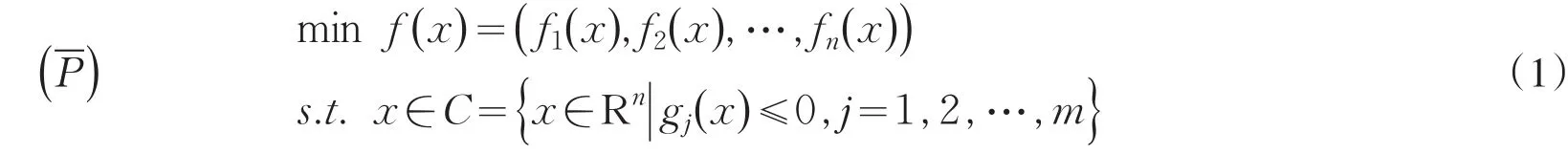
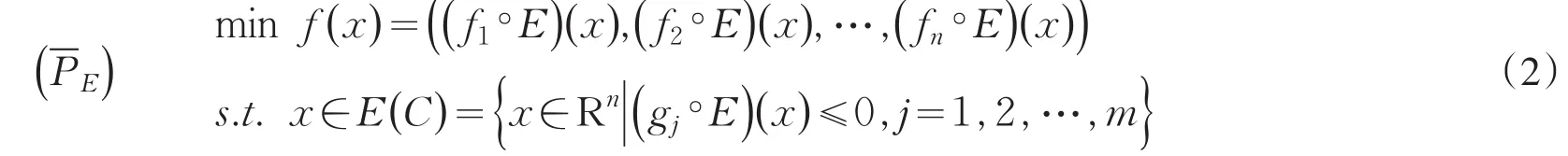
关于上述两种规划问题的最优解研究结果有很多，其中Youness E A在文献[1]中给出的定理4.1（即:问题的解集C是E-凸集）有错误之处.Chen和覃义等分别在文献[4]和[6]中给出该定理的反例和适当的修正.下面是本文给出的该定理的另一个反例：

2 E-凸规划最优解与最优性条件

定义1[10]称点是问题的最优解当且仅当对于所有的x∈C都有：

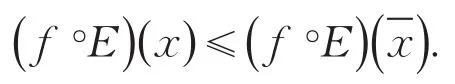
引理1[4]若C是E-凸集，实值函数f∶C⊆Rn→R为C上的E-凸函数，且满足对任意的x∈C成立，如果是问题的最优解，那么是问题的最优解.

引理2[4]若实值函数f∶C⊆Rn→R为E-凸集C上的严格E-凸函数，其中E()C是凸集，则凸规划问题的最优解唯一.

引理3[1]已知C是E-凸集，是凸集，且f∘E和gi∘E(i=1,2,…,m)在C上均是可微的，若是如下问题的最优解：

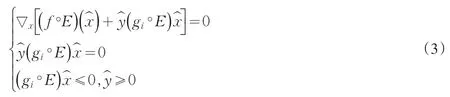
通过限定映射E∶Rn→Rn为满射，对Youness E A的定理4.2进行适当修正得到下面的定理1，之后本文还给出关于E-凸规划的一个最优性充分条件（见定理2）.

定理1 令映射E∶Rn→Rn是一个满射，则是E-凸规划问题的最优解当且仅当是问题的一个最优解.

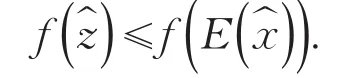
因为E∶Rn→Rn是满射，所以有：E()C=C，故存在一个满足：从而可得：

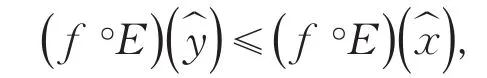
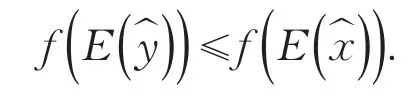
因为E∶Rn→Rn是满射，故存在一个满足：从而可得：这显然与是问题的一个最优解相矛盾.故假设不成立，所以是问题的一个最优解.

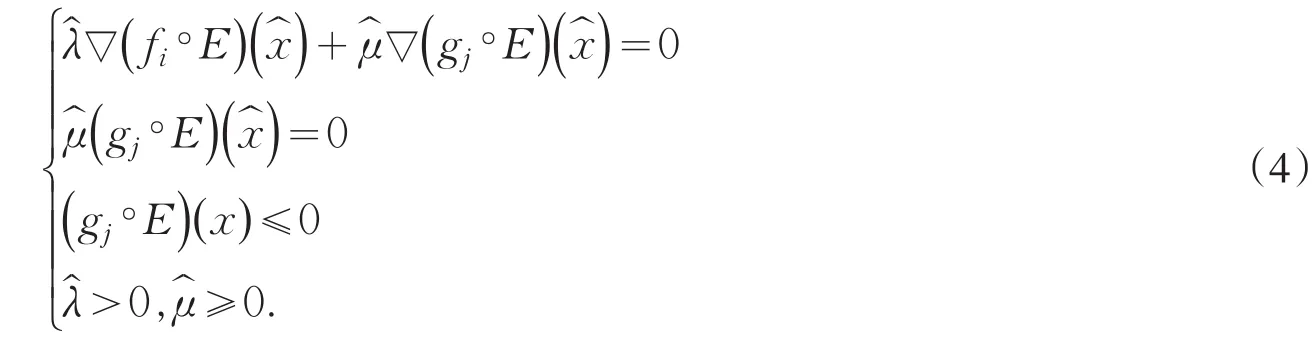
因为fi和gj均为E-凸函数，而且fi∘E和gj∘E均为可微函数，故对任意x∈(E)

M，我们有：

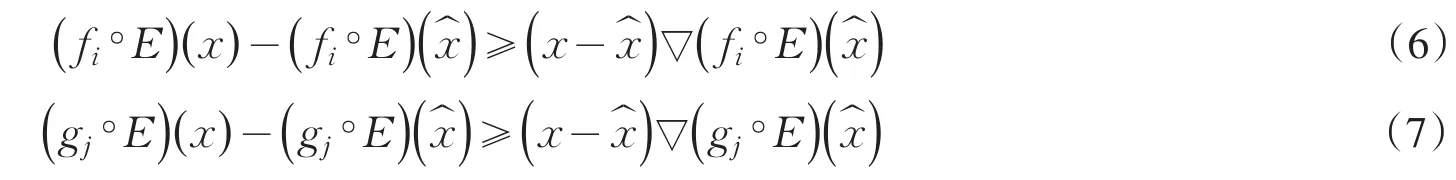
因为由已知条件，＞0,≥0，结合（6）与（7），对每个i,j∈N*，有：

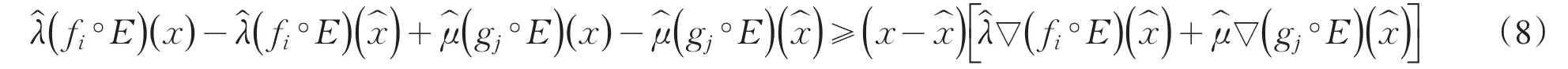
显然，（5）与（9）的结果产生了矛盾，故假设不成立，所以是问题的一个最优解.

注1：当fi变为严格E-凸函数，＞0变为≥0，定理2的结论仍然成立.

例2 考虑下面的E-凸规划问题：

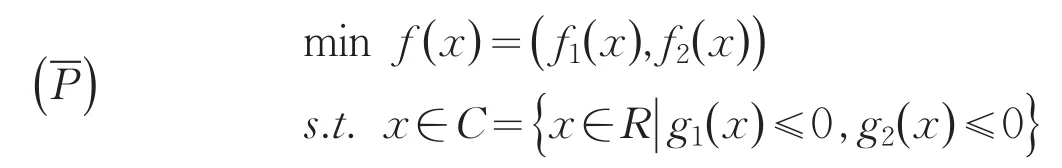
3 结语

本文是给出了一个E-凸规划问题的最优性充分条件，并在E-可微情形下研究得到E-凸规划问题的最优解相关结论，在一定程度上丰富了前人关于E-凸最优性方面的研究内容，扩大了（广义）E-凸性在优化理论与应用领域的影响.关于E-凸规划最优性方面的研究还有很多工作可做，特别是广义E-凸函数的出现，极大地促进了E-凸规划相关理论的研究进展，这也是将来继续研究的主要方向.

[1]Youness E A.E-convex sets,E-convex functions,E-convex programming[J].Journal of Optimization Theory and Applica⁃tion，1999，102（2）：439-450.

[2]Youness E A.Optimality criteria in E-convex programming[J].Journal of Optmization Theory and Applications，2001，12（9）：1737-1745.

[3]Yang X M，Teo K L，Yang X Q.A characterization of convex functions[J].Applied Mathematics Letter，2000，13（1）：27-30.

[4]Chen X S.Some properties of semi-E-convex functions[J].Journal of Mathematics Analysis and Applications，2002，275（1）：251-262.

[5]Jian J B.Incorrect result for E-convex sets,E-convex function and E-convex programming[J].Mathematiccal Research and Exposition，2003，23（3）：461-466.

[6]覃义，简金宝.关于E-凸函数及E-凸规划的几个错误结论的修正[J].数学杂志，2006，26（2）：177-180.

[7]Youness E A.Characterization of efficient solutions of multi-objective E-convex programming problems[J].Journal of Applied Mathematics and Computation，2003，151（3）：755-761.

[8]Youness E A，Emam T.Characterization of efficient solutions for multi-objective optimization problems involving semi-strong and generalized semi-strong E-convexity[J].Acta Mathematica Scientia，2008，28（1）：7-16.

[9]Megahed A A，Youness E A.A combined interactive approach for solving of E-convex multiobjective nonlinear programming problem[J].Applied Mathematics and Computation，2011，217（16）：6777-6784.

[10]Megahed A A，Gomma H G，Youness E A.Optimality conditions of E-convex nonlinear programming for E-differential func⁃tion[J].Journal of Inequalities and Applications，2013，246（1）：1-11.

责任编辑：吴兴华

The Study of Optimality ofE-convex Programming

WANG Shilei
（School of Mathematics and Information，Xinyang University，Xinyang464000，China）

This paper first presents a counter example of the theorem 4.1 in reference[1]and gives the characterization of the optimal solution of theE-convex programming problem by making revision of the theorem 4.2 in reference[1].Then it gives sufficient conditions of theE-convex programming.Finally,it studies the relevant conclusion of the optimal solution of theE-convex programming for theE-differentiable case.

E-convex function；E-convex programming；E-differentiable；optimal solution；optimal condition

O 174.13

A

1674-4942（2017）01-0001-06

2016-10-17

*通讯作者：王世磊，硕士，E-mail：ge_wangshilei@163.com

10.12051/j.issn.1674-4942.2017.01.001