强化例题教学，提升数学课堂效益

唐正彪

摘要：数学是是一种灵活性和应用型都比较较强的科目。如果学生在学习数学时仅仅停留于理论知识的学习，恐怕很难将知识学习得透彻清楚。因此，教师需要为学生强化典型例题的讲解，让学生在例题的学习研究中运用所学到的理论知识，进一步理解和掌握数学中的公式、概念、运算法则。

关键词：数学教学；例题教学；课堂效益

中图分类号：G633.6 文献标识码：B文章编号：1672-1578（2017）03-0078-02

对于初中数学教学来说，例题教学是一种非常重要的教学方法。例题的讲解能够帮助学生把学习的理论知识和数学方法、解题技巧结合起来，提高学生的解题能力。教师通过例题的讲解，向学生示范解题过程，分析思路，以及规范的书写过程，学生也会由此潜移默化地受到影响和熏陶，进而在思维和行为上得到提升。故而，强化课堂上的例题教学，能有效提高课堂效益。下面是笔者就初中数学例题讲解的一些经验总结，愿与诸君共享，希望能够抛砖引玉，在例题教学方面共同提升。

1.一题多解，"通"思路

例题讲解的示范性作用可以帮助学生在面对题目时，找到分析题目的思路和方法，教师向学生展示怎样从题目中所给的条件到达最终要求的量或者推出要证明的结论，根据条件，示范不同的解法路径，一题多解，从多个方向讲解题目，为学生打开思路，理清头绪，破除思维定势，培养学生面对问题时的独立思考能力。

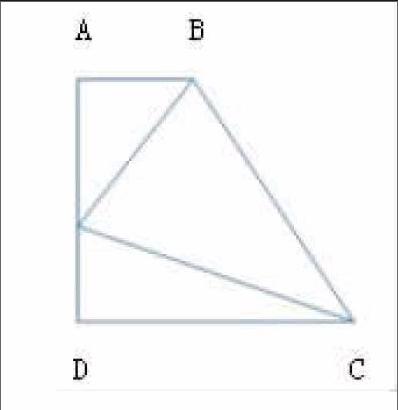
以接下来的几何题目为例，如上图所示，已知，AB=AE，AC=AD，求证 BC=DE.首先可以这样看，题目中给出的条件AB=AE，AC=AD为我们构造了两个等腰三角形：三角形ABE和三角形ACD，等腰三角形有一个最常见的特性就是三线合一，可以做高线AH，则有CH=DH，BH=EH，进而可以推出BH-CH=EH-DH即BC=DE得证。除此之外，由已知条件证三角形全等是初中阶段常用的一种证明线段相等的常用手段。在这里可以证明三角形ABC和三角形ADE全等或者三角形ABD和 三角形ADE 全等，这时就可以用边角边，角边角等等。这样通过证明全等，可以拓展多种方法。

利用等腰三角形或者三角形全等来证明线段相等在初中数学阶段非常常见，上面的例子中，一道题将这两种方法都运用起来，帮助学生拓宽思路，选择合适自己的解题思路和解题方法。通过一题多解，学生可以找到知识之间的相通之处，理通思路。

2.深度探究，"透"思想

在数学的学习中，数学思想方法的学习尤为重要，新课标中也把数学思想认定为数学学习的重点。数形结合、分类讨论、方程和函数等都是在初中阶段重要的学习思想 。教师在进行典型例题展示时，可以通过深入探究例题本质，挖掘题目中蕴含的数学思想，逐渐在课堂学习过程中向学生渗透数学思想。

在二次函数的教学中，有这样一道例题：已知关于X的二次函数为（c>0），对称轴为x=2，函数的图像与y轴相交于点A，与x轴相交于点M、N且OM0，可以知道点A在正半轴，再根据OC=3可以得出c=3.假设N点位于负半轴（-3，0），则根据对称轴X=2可以计算出M点为（7，0）这时OM=7，与题目中OM

上面例子中数形结合的思想将代数运算的严密和几何分析的直观形象结合起来，学生运用数形结合思想可以更加灵活、清晰地分析题目，求解题目。多种数学思想的渗透可以培养学生的数学思维，提高解题能力。

3.探寻规律，"变"思维

数学是一个非常具有灵活性的科目，它的题目千变万化，稍微有所改动就有可能使题目发生非常大的改变。面对这种情况，就需要教师在讲解例题时从多个方面，多个角度对题目本质进行深度阐释，在变化中把握不变的基本规律，再利用基本规律去解决变化的题目，培养学生"变"的思维。

以下面题目为例：梯形ABCD如图所示，AB//CD，且AB=1，CD=3，BD=4，E为AC的中点，求证BE垂直于DE.分析这道题目时可以先做一条辅助线：从B点作线段 BH垂直CD与H，则DH=1，CH=2根据勾股定理可以求出AD=BH=23，则可以由此再用勾股定理求出BE和CE：BE=1+3=2=2，CE=9+3=23，在根据计算可以得出边长BE、DE和BD满足 E 勾股定理的条件，故而BE 垂直于DE得证。我们知道这是一道关于勾股定理知识考察的题目，学生做完之后教师可以做这样的改动：梯形ABCD如图所示，AB//CD， E为AC的中点，且 BE垂直于DE求证BC=AB+DC.改动之后再次进行分析：由AB与AD/2可以表示BD，DC和AD/2可以表示CE，由BE和CE可以表示BC，这样就相当于用AB，CD，AD表示BC，又由于AD可由BC和（DC-AB）表示，最后可以建立一个只有AB、CD、BC的等式，通过化简得到想要的结果。

上面这道题目还有很多变换的方法，但是我们从两次分析中可以看到，这道题分析时主要看勾股定理和各边长之间的关系，掌握了这个规律特点，无论题目条件怎样变化，解题运用的方法规律都会有一定的固定性。

4.引导质疑，"悟"方法

数学的学习应该是一个主动体悟的过程，因此，在进行例题教学时，教师应该引导学生主动进行质疑，思考这道题目为什么是用这样的解题思路，为什么要往这个方向考虑和推导，这个过程，就是学生在体悟解题方法的过程，只有学生主动质疑，主动思考，才能清楚地理解和掌握解题方法。

仍旧以一道几何题为例：在三角形ABC中，角A=180，且AB=AC，BD是角ABC的平分线，求证BC=AB+CD。在这道题目中，根据题目所给条件，很容易找到角的关系，最后所求却是边之间的关系，可以在边BC上截取BE=BA，这时证明CE=CD即可使题目得解。在本题目中知道角较多，因此可以尝试将可以求出的角写出，最后找到一个等腰三角形CDE，使得CD=CE，题目解出。然而，学生定会对此非常困惑，为什么教师可以找到合适的辅助线解出题目呢？怎么找到的突破点BE呢？在题目中，三条边毫无联系，也没有一些其他的代数公式可以推导，所以就要想办法制造边和边之间的联系，于是采用截取方法，将原来的线段相加问题变成了证明线段相等问题，降低了证明难度。

在上例中，教师通过例题向学生展示了作辅助线的一种思路方法。怎样做出合适的辅助线一直也是初中数学的难点，因为毫无头绪可言，全靠学生的摸索和探究。类似于这种数学问题，就需要学生主动质疑思考解题方向，不断内化，体悟解题方法。

总而言之，在例题教学中，教师应该充分重视学生对解题思路的掌握，思考思维方式的熏陶和培养。强化例题教学，让学生通过经典例题的学习，抓住解题规律，掌握题目本质，提高课堂学习效率，在千变万化的题目当中也可以以不变应万变，游刃有余地解答题目。

参考文献：

[1] 严雪莲.初中數学例题及习题教学研究[J].教育科学，2016（12）.

[2] 周梨.浅谈初中数学的例题教 学[J].教育，2016（12）.