一种简化的拟蒙特卡洛-高斯粒子滤波算法*

高国栋，林 明

(江苏科技大学 电子信息学院，江苏 镇江 212003)

一种简化的拟蒙特卡洛-高斯粒子滤波算法*

高国栋*，林 明

(江苏科技大学 电子信息学院，江苏 镇江 212003)

提出了一种简化的拟蒙特卡洛-高斯粒子滤波(QMC-GPF)算法(SQMC-GPF),以解决将QMC方法应用于GPF时计算复杂度高、运算量大的问题。该算法中，在连续的迭代滤波过程开始之前，首先利用QMC采样产生单位拟高斯分布粒子集，然后用其线性变换产生GPF算法中需要的高斯分布粒子集，省去了重新进行QMC采样步骤。该算法简化了新粒子集的产生过程，减少了运算量和滤波时间，增强了算法的实时性。将粒子滤波算法(PF)、GPF 算法、QMC-GPF算法和SQMC-GPF算法用于单变量非静态增长模型(UNGM)和二维纯角度跟踪模型(BOT)的仿真结果表明，SQMC-GPF算法的滤波性能与QMC-GPF算法的滤波性能相近，但有更为明显的速度优势，具有重要的实际应用价值。

高斯粒子滤波；拟蒙特卡洛采样；线性变换；高斯分布

1 引 言

高斯粒子滤波(Gaussian Particle Filter,GPF)[1]是粒子滤波(Particle Filter,PF)[2]的改进算法，用高斯分布来近似状态的后验分布，用蒙特卡洛(Monte Carlo,MC)[3]方法模拟高斯分布采样，替代了对全体粒子状态的存储，避免了重采样过程，因此减少了运算量，提高了算法的滤波效率。为进一步提高精度，很多学者对GPF算法进行了研究和改进，其中一种就是改进MC采样方法。文献[4]对GPF算法进行了分析，并首次提出在GPF算法的框架内，运用拟蒙特卡洛确定性(Quasi-Monte Carlo,QMC)采样[5]代替MC伪随机采样的构想。文献[6-8]分别给出QMC-GPF算法流程，并用于目标跟踪，取得了较好的滤波效果，但没有讨论算法的实时性问题。文献[9]为了提升QMC-GPF算法的实时性，研究并给出了该算法的FPGA实现方案，将QMC采样分为多组并行单元同时进行，采样完成后再进行拟高斯序列的转换，但具有较高的实现复杂度和较高硬件资源需求。

QMC方法是MC方法的一个变种，利用确定的低差异拟随序列代替“随机的”伪随序列，因而具有更快的误差收敛速度，且误差是确定的[10]。QMC采样致力于给出差异度最低、分布得“最均匀”的确定点列[5]，由此可以推断，对于在某一固定空间上的求解问题，一次高质量的QMC采样即具有代表性，无需重复多次。而在QMC-GPF算法中，连续迭代滤波都需要重复调用QMC方法产生超均匀序列，因此基于以上推断，本文对QMC-GPF算法进行简化，提出SQMC-GPF算法，即在滤波前进行QMC采样，生成高质量的超均匀样本集，然后通过变换得到单位拟高斯分布序列，以其线性变换代替每一时刻迭代滤波中的QMC分布采样，从而降低算法的复杂性和运算量，提高运算速度。

2 算法原理及分析

2.1 QMC-GPF算法原理及分析

QMC方法用确定性超均匀序列来模拟采样空间中点的可能性分布，提高了点的利用率[10]。在计算机中，MC方法通常用确定的数学公式产生伪随机数，用得比较多的是m序列法。QMC方法常采用的低偏差序列[11]包括Sobol序列、Faure序列和Halton序列等。本文选用Halton序列法生成拟随机序列，然后再采用经典的Box-Muller方法[12]，把超均匀分布的随机数转换为单位拟高斯随机数，其算法步骤如下：

步骤1 运用m序列法产生两个随机正整数n1和n2。

步骤2 根据Halton序列[11]产生原理，生成两列个数为N的拟随机序列：

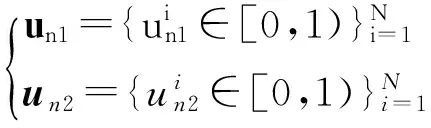
(1)

步骤3 用Box-Muller方法产生单位拟高斯随机序列：

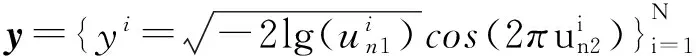
(2)

或者

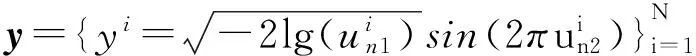
(3)

步骤4 根据高斯分布的线性不变性，将服从单位拟高斯分布的序列转换为均值为m，协方差为Q的高斯分布序列。首先对协方差矩阵Q进行Cholesky分解：Q=RTR，然后通过线性变换得到拟高斯序列：

x=Ry+m。

(4)

用QMC方法替换GPF算法中的MC方法就得到QMC-GPF算法[9]。本文以先验概率密度函数p(xn|xn-1)作为重要性密度函数π(xn|y0:n)，其算法步骤如下：

步骤1 初始化过程。根据先验知识，设定初始状态的均值μ0和协方差Σ0。

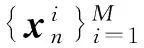
步骤3 量测更新过程。按式(5)计算重要性权值:

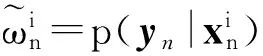
(5)

并权值归一化：

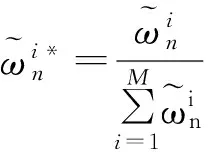
(6)

步骤4 估计n时刻状态的均值和协方差：

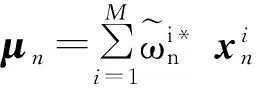
(7)

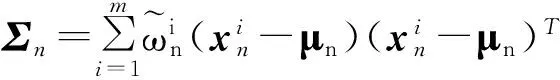
(8)

由QMC-GPF算法步骤可知，每一次的时间更新过程都需要进行一次QMC采样及其转换操作；而且在多维的情况，为保证精度，QMC方法得到的低差异度序列必须保证其二维投影服从均匀分布，这需要对原始拟随机序列进行额外的随机化操作，从而将导致QMC-GPF算法的复杂度与运算时间的增加。

2.2 SQMC-GPF算法

将QMC方法用于GPF算法中，实则是改变GPF算法中样本粒子的采样方式。本文提出的简化QMC-GPF算法，用对基本粒子集的线性变换取代了每次迭代滤波中的高斯分布采样，只要在滤波开始前用QMC方法准备好单位拟高斯随机序列即可，在滤波过程中无需重新调用QMC方法。SQMC-GPF算法流程如下：

步骤2 初始化过程。根据先验知识，设定初始状态的均值μ0和协方差Σ0。

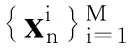
步骤4 量测更新过程。按式(5)和式(6)计算重要性权值，并将其归一化。

步骤5 按式(7)和式(8)，估计n时刻状态的均值和协方差。

根据以上算法步骤，在SQMC-GPF算法中，只需要在滤波开始前进行一次QMC采样和BoxMuller方法生成单位拟高斯序列，然后用其线性变换来代替时间更新过程中的高斯分布采样，因此QMC采样和BoxMuller方法虽然需要大量的运算时间，但只运行一次，所以并没有影响滤波的实时性。用线性变换产生一个高斯随机数，只需要1次乘法、1次加法和很少硬件资源；运用Halton序列和BoxMuller方法产生一个高斯随机数，至少需要2次查找判断操作、2次异或操作[13]、1次乘法、1次三角函数运算、1次开方运算和1次对数运算等，即使在BoxMuller方法阶段运用查找表法极大提高运算速度，整体的运算时间和所需要的资源也都远远超过线性变换。所以SQMC-GPF算法能显著减少算法的运算时间，尤其当粒子数量很大时，这种优势更加明显。

因为本文算法是运用单次QMC方法代替多次QMC方法，所以单次进行的QMC采样产生的拟随机序列的均匀性直接决定估计的精度和稳定性。可以先对拟随机序列进行随机化操作，以消除不同维之间的相关性，提高经式(2)或式(3)转换而成的拟高斯序列的质量。

3 仿真实验及分析

本文采用文献[14]和文献[15]中用到的两种经典非线性模型分别在估计精度、估计稳定性和计算时间3个方面来验证算法的有效性：变量非静态增长模型(UnivariateNonstationaryGrowthModel,UNGM)和二维纯方位跟踪(2DimensionBearing-OnlyTracking,BOT)模型。其中UNGM模型普遍应用于经济领域，其高度的非线性以及其状态量分布的双模态性，使其经常作为验证非线性滤波算法的基准模型。纯方位跟踪(Bearing-OnlyTracking,BOT)是一类典型的目标运动分析问题，常用于被动跟踪系统中，由于其隐蔽性好，抗干扰性强，历来是研究的热点和难点。由于系统本身的弱观测性和状态空间模型的强非线性，卡尔曼等传统滤波方法在精度方面往往不能满足要求。在处理纯方位跟踪问题，粒子滤波算法有很好的表现。

3.1UNGM模型的仿真

UNGM模型状态空间方程为

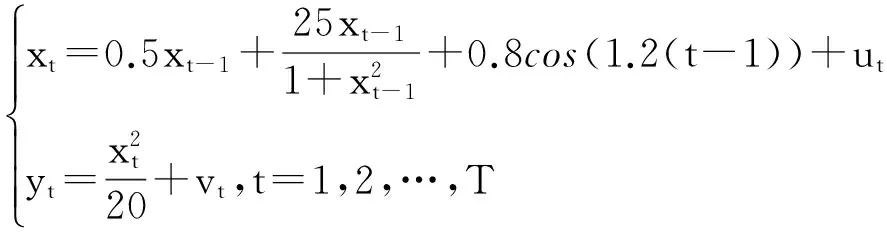
(9)

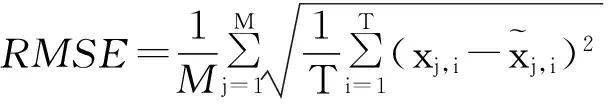
(10)

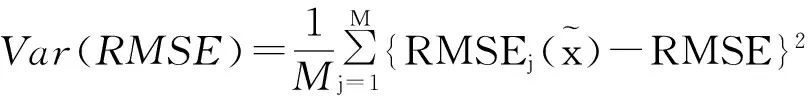
(11)

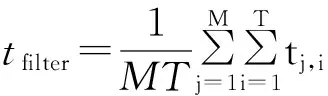
(12)

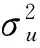
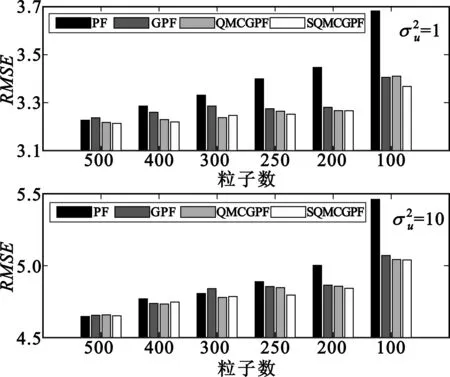
图1 PF、GPF、QMC-GPF和SQMC-GPF算法估计误差的比较

图2是估计稳定性的比较，从图中可以看出，SQMC-GPF算法在粒子数超过300时，估计稳定性接近于GPF和QMC-GPF算法，说明其继承了QMC-GPF算法稳定性的优点。当粒子数量不超过250时，SQMC-GPF算法的稳定性优于其他3种算法，原因是SQMC-GPF算法用确定性采样代替了伪随机采样，用单次高质量的QMC采样代替了多次“伪随机”QMC采样，减少了不确定性，因而具有更好的稳定性。进一步比较可发现，当过程噪声的方差不同时，SQMC-GPF算法依然保持较好的滤波精度和稳定性，说明其有较强的鲁棒性。

图2 PF、GPF、QMC-GPF和SQMC-GPF算法估计误差方差的比较

图3为4种算法单次滤波运行时间的比较，可以明显看出，QMC-GPF算法所需要的时间远超过其他3种算法，说明其获得高精度估计的同时，损失了实时性，而SQMC-GPF算法因为用线性运算代替了拟高斯分布采样，其所需时间远低于QMC-GPF算法。同时可以看到，粒子数量越大，运算时间上的优势越明显，验证了算法分析的结论。

图3 PF、GPF、QMC-GPF和SQMC-GPF算法单次滤波运算时间的比较

3.2 BOT模型的仿真

BOT模型仅通过方位角度来对目标进行跟踪。在直角坐标系下，模型的状态方程和观测方程分别为

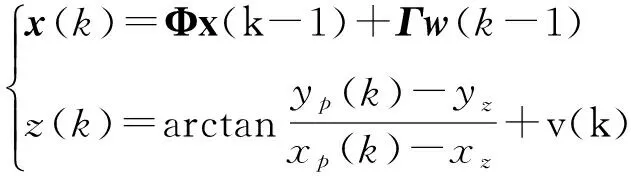
(13)

表1 粒子数为100时PF、GPF、QMC-GPF和SQMC-GPF算法的跟踪性能比较

表2 粒子数为500时PF、GPF、QMC-GPF和SQMC-GPF算法的跟踪性能比较

在表1和表2中，通过对4种算法在x、y方向的位置和速度估计精度的比较可以得出,在粒子数量较少(100)或者在粒子数量较多(500)的条件下，SQMC-GPF算法的跟踪精度与QMC-GPF相近，且两种算法都优于GPF和PF算法，且在粒子数量为较少时更明显，这与UNGM模型仿真分析得到的结论一致。通过对稳定性的比较可以发现，当该模型有500个粒子时，SQMC-GPF算法的稳定性比QMC-GPF稍差，但在100个粒子时，这种差距变得很小，这同样说明SQMC-GPF算法在粒子数量少时具有较好的稳定性。最后，滤波时间的比较再次证明了SQMC-GPF算法的快速性。

图4是其中一次目标跟踪结果，图中PF跟踪算法出现了发散，SQMC-GPF和QMC-GPF算法均能较好地实现目标跟踪。

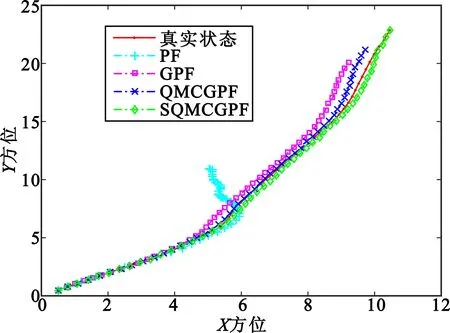
图4 PF、GPF、QMC-GPF和SQMC-GPF算法的跟踪结果

综合上述仿真实验可知，在不同的粒子数量下，SQMC-GPF算法估计精度和稳定性都接近于QMC-GPF算法，且在绝大多数情况下都优于GPF和PF算法；当粒子数量较少时，SQMC-GPF算法具有相对于其他3种算法较好的估计稳定性;同时,SQMC-GPF算法在运算时间方面都优于其他3种算法，具有较强的实时性。

4 结束语

本文分析了QMC-GPF算法的优缺点，提出了SQMC-GPF算法，以线性变换代替原算法中的高斯分布采样，即运用一次QMC方法代替多次QMC方法，大大提高了运算速度。仿真实验表明，SQMC-GPF算法在提高速度的同时，估计性能接近于QMC-GPF算法，使得QMC方法与GPF算法结合产生的实时性问题得以解决，具有重要的实际应用价值。本文的下一步工作就是研究SQMC-GPF算法的硬件实现结构，在实际应用背景下验证该算法的可靠性。

[1] KOTECHA J H,DJURIC P M. Gaussian particle filtering[J].IEEE Transaction on Signal Processing,2003,51(10):2592-2601.

[2] 王法胜,鲁明羽,赵清杰,等. 粒子滤波算法[J].计算机学报,2014,37(8):1679-1694. WANG Fasheng,LU Mingyu,ZHAO Qingjie,et al. Particle filtering algorithm[J].Chinese Journal of Computer,2014,37(8):1679-1694.(in Chinese)

[3] CHEN R. Sequential Monte Carlo methods for dynamic systems[J].Journal of the American Statistical Association,2014,93(443):1032-1044.

[4] WU Y,HU X,HU X,et al. Comments on Gaussian particle filtering[J].IEEE Transactions on Signal Processing,2005,53(8):3350-3351.

[5] LEMIEUX C. Monte Carlo and quasi-Monte Carlo sampling[J].Berlin:Springer,2009.

[6] 陈曦. 基于粒子滤波的检测前跟踪算法研究[D].西安：西安电子科技大学,2009. CHEN Xi. Sdudies on track before deteck algorithm based on particle filter[D].Xi′an:Xidian University,2009.(in Chinese)

[7] 武斌,李鹏. 一种新的红外弱小目标检测前跟踪算法[J].西安电子科技大学学报(自然科学版),2011,38(3):107-113. WU Bing,LI Peng. Novel track-before-detect algorithm for small infrared target[J].Journal of Xidian University,2011,38(3):107-113.(in Chinese)

[8] 张俊根,赵培宇. 基于QMC-GPF的被动测角目标跟踪算法[J].控制工程期刊(中英文版),2013,3(2):52-58. ZHANG Jungen,ZHAO Peiyu. Quasi-Monte Carlo Gaussian particle filter based passive bearing-only target tracking[J].Scientific Journal of Control Engineering,2013,3(2):52-58.(in Chinese)

[9] 李倩,姬红兵,郭辉. 拟蒙特卡洛-高斯粒子滤波算法研究及其硬件实现[J].电子与信息学报,2010,32(7):1737-1741. LI Qian,JI Hongbin,GUO Hui. Research and hardware implementation of quasi-Monte Carlo Gaussian particle filter[J].Journal of Electronics & Information Technology，2010,32(7):1737-1741.(in Chinese)

[10] RUSSEL E,CAFLISCH. Monte Carlo and quasi-Monte Carlo methods[M]// Functionals of Multidimensional Diffusions with Applications to Finance.Berlin:Springer International Publishing,2013:343-358.

[11] 朱平. 拟蒙特卡洛方法的若干研究与应用[D].杭州：浙江大学,2010. ZHU ping. Thestudies and application of quasi Monte Carlo methods[D].Hangzhou:Zhejiang University,2010.(in Chinese)

[12] 陈雷成,王华华,江彦鲤,等. 一种低复杂度信道模拟器的设计[J].电讯技术,2014,54(9):1275-1279. CHEN Leicheng,WANG Huahua,JIANG Yanli,et al. Design of a low complexity channel simulator[J].Telecommunication Engineering,2014,54(9):1275-1279.(in Chinese)

[13] DALAL I L,STEFAN D,HARWAYNE-GIDANSKY J. Low discrepancy sequences for Monte Carlo simulations on reconfigurable platforms[C]//International Conference on Application-Specific Systems,Architectures and Processors(ASAP).Leuven,Belgium:IEEE,2008:108-113.

[14] 李海君,赵国荣. 基于快速高斯变换的辅助边缘粒子滤波算法[J].数据采集与处理,2014,29(6):998-1002. LI Haijun,ZHAO Guorong. Auxiliary marginal particle filter algorithm based on fast Gaussian transformation[J],Journal of Data Acquisition Processing,2014,29(6):998-1002.(in Chinese)

[15] 李善姬,禹爱兰. 一种改进重采样的粒子滤波算法[J].电讯技术,2011,51(9):35-38. LI Shanji,YU Ailan. An improved resampling particle filtering algorithm[J].Telecommunication Engineering,2011,51(9):35-38.(in Chinese)

A Simplified Quasi-Monte Carlo Based Gaussian Particle Filter

GAO Guodong,LIN Ming

(School of Electronics Information,Jiangsu University of Science and Technology,Zhenjiang 212003,China)

A simplified Quasi-Monte Carlo Gaussian particle filtering(QMC-GPF)(SQMC-GPF) algorithm is presented to solve the problems of high complexity and large amount of computation that QMC method is faced with when it is applied to GPF. In this algorithm,a basic set of particles which obey unit quasi-Gaussian distribution are pregenerated with the method of QMC before the successive iterative filering process,and then they are converted to the particles needed during iterative filering by means of linear transformation,without the QMC method called again. This algorithm simplifies the generation of new particles,reduces the amount of computation and filtering time,and improves the real-time performance of the QMC-GPF algorithm. Finally,the PF,GPF,QMC-GPF and SQMC-GPF algorithms are simulated with univariate nonstationary growth model(UNGM) and bearing-only tracking model(BOT).Results show that,SQMC-GPF algorithm has much higher filtering speed than QMC-GPF algorithmon on the premise of the same filtering performance,which proves that the former has important practical application value.Key words：Gaussian particle filter;quasi-Monte Carlo sampling;linear transformation;Gaussian distribution

10.3969/j.issn.1001-893x.2017.04.015

高国栋，林明.一种简化的拟蒙特卡洛-高斯粒子滤波算法[J].电讯技术，2017,57(4):457-462.[GAO Guodong,LIN Ming.A simplified quasi-Monte Carlo based Gaussian particle filter[J].Telecommunication Engineering,2017,57(4):457-462.]

2016-07-08；

2016-09-28 Received date:2016-07-08；Revised date：2016-09-28

国家自然科学基金资助项目(61401179)

TN713

A

1001-893X(2017)04-0457-06

高国栋(1990—)，男，江苏淮安人，硕士研究生，主要研究方向为信号与信息处理；

Email:ggdffic@163.com

林 明(1960—)，男，辽宁大连人，教授、研究生导师，主要研究方向为雷达信号处理、船舶电子。

*通信作者：ggdffic@163.com Corresponding author：ggdffic@163.com